北京市西城区三十五中2012年八年级下学期期中考试试题及答案
文档属性
| 名称 | 北京市西城区三十五中2012年八年级下学期期中考试试题及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 119.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-09 00:00:00 | ||
图片预览



文档简介
2011—2012学年度第二学期北京市第三十五中学期中质量检测
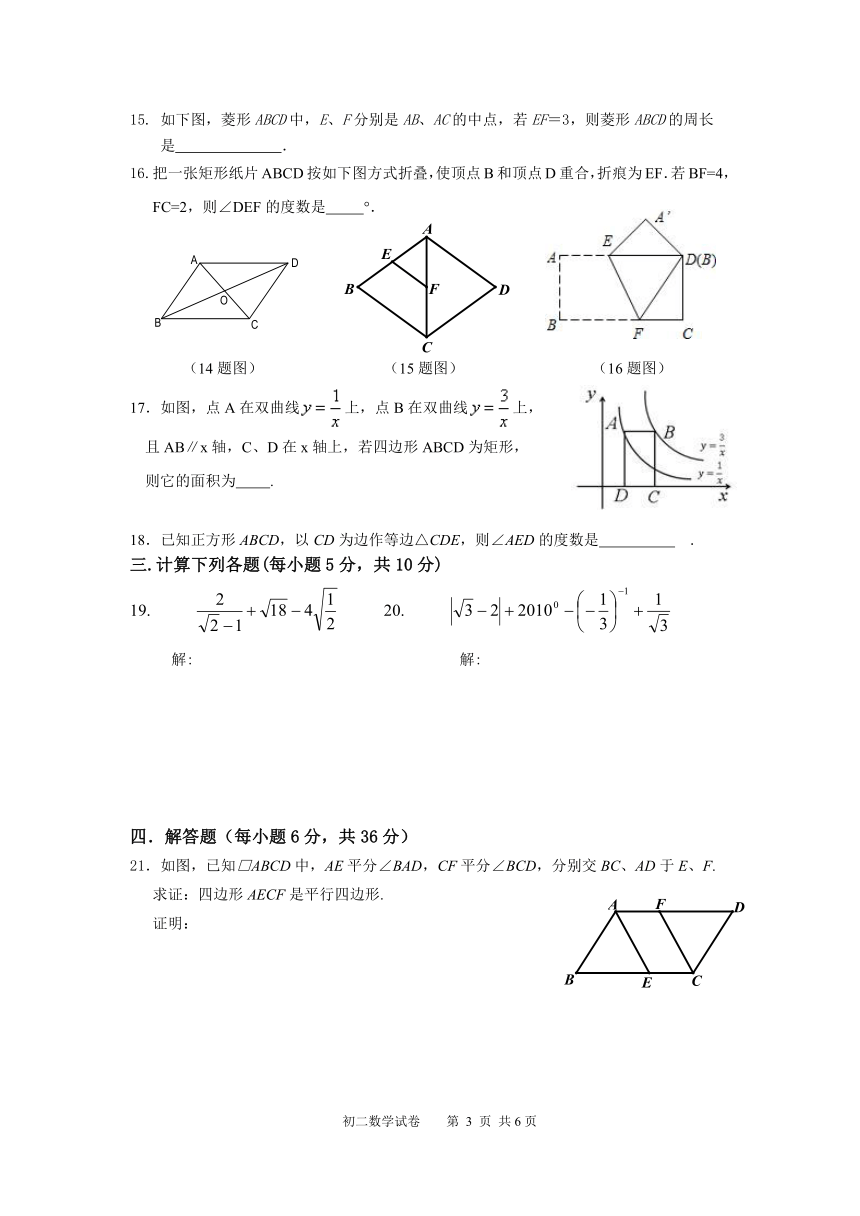
初 二 数 学
试卷说明:1、本试卷共6页,计四类大题,26道小题;2、本次考试卷面分值100分,考试时间为90分钟;3、认真审题,所有试题全部在卷面作答。
一、选择题(每小题的四个选项中,只有一个是符合题目要求的.请将你认为符合要求的一项的序号填在题中的括号内.每小题3分,共30分)
1. 下列二次根式中,属于最简二次根式的是( ).
A. B. C. D.
2. 已知反比例函数y =的图象在第二、四象限,则m的取值范围是( ).
A. m≥5 B. m>5 C. m≤5 D. m<5
3. 下列各式中,计算正确的是( ).
A. B.
C. D.
4. 直角三角形的两条直角边的长分别为5,12,则斜边上的中线为( ).
A. cm B. 13cm C. 6cm D. cm
5. 下列各组数中, 能成为直角三角形的三条边长的是 ( ).
A.9, 80, 81 B. 10,24,25 C. 9 ,15,20 D. 8,15,17
6. 已知一次函数y1=kx+b与反比例函数y2=在同一直角坐标系中的图象如图所示,
则当y1<y2时,x的取值范围是( )
A.x<﹣1或0<x<3 B.﹣1<x<0或x>3
C.﹣1<x<0 D.x>3
7. 已知正比例函数的图象与反比例函数的图象的一个交点坐标是,则另一个交点的坐标是( ).
A. B. C. D.
8. 如图,在□ABCD中,已知AD=8cm,AB=6cm,
DE平分∠ADC交BC边于点E,则BE等于( ).
A.2cm B.4cm C.6cm D.8cm
9. 如下图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
A.14 B.16 C.20 D.28
10.如图,四边形ABCD中,AC=a,BD=b,且AC丄BD,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是
④四边形AnBnCnDn的面积是.
A、①② B、②③ C、②③④ D、①②③④
(第9题) (第10题)
二.填空题(请将正确答案填在题中的横线上.每空3分,共24分)
11. 使式子有意义的条件是 .
12. 若,则 .
13. 梯形的上底长为6cm,过上底的一顶点引一腰的平行线,交下底所构成的三角形周长为21cm,那么该梯形的周长是 .
14. 如下图,□ ABCD的对角线相交于点O,两条对角线的和为18,AD的长为5,则OBC的周长为 ___________.
15. 如下图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长
是 .
16.把一张矩形纸片ABCD按如下图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数是 °.
(14题图) (15题图) (16题图)
17.如图,点A在双曲线上,点B在双曲线上,
且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,
则它的面积为 .
18.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是 .
三.计算下列各题(每小题5分,共10分)
19.20. 解: 解:
四.解答题(每小题6分,共36分)
21.如图,已知□ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.
求证:四边形AECF是平行四边形.
证明:
22..如图,梯形ABCD中, AD//BC, ∠ABC=45 , ∠ADC=120 ,
AD=DC,AB=,求BC的长.
23.已知一次函数的图象与反比例函数的图象交于点、.(1)求一次函数和反比例函数的解析式;(2)求△MON的面积.
(1)解:
(2)解:
24.如图,在平面直角坐标系中,双曲线y= 过点A(-4,1),点P是双曲线上一动点(不与A重合),过点A和P分别向两坐标轴作垂线,垂足分别为B、C和D、E.
(1)求k、S△ADC及S△PDC的值;
(2)判断AP和DC的位置关系,并说明理由;
(3)若点P在双曲线上运动时,探索以A、P、C、D四点为顶点的四边形能否成为菱形和等腰梯形?若能,请直接写出所有满足条件的点P的坐标;若不能,请说明理由.
25.如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连结EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° , ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF,
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
⑵方法迁移:
如图②,将沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
26.如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)若∠1=70°,求∠MKN的度数;
(2)△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.
2011—2012学年度第二学期北京市第三十五中学期中质量检测
初 二 数 学 答 案
一 、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B D D B A A D C
二、填空题
11 12 13 14 15 16 17 18
14 24 60° 2 15°或75°
三、解答题
19、 原式= 20、原式=
21、 略
22、 解:解:如图,过A作AE⊥BC于E, 连接AC.
∴ ∠AEB=∠AEC=90.
∵ ∠ABC=45,AB=,
∴ AE=BE =2. ………………2分
∵ AD//BC, ∠ADC=120,
∴ ∠1=∠2, ∠D+∠DCB=180.
∴ ∠DCB=60. ………………………………………………………………………3分
∵ AD=DC,
∴ ∠1=∠3.
∴ ∠2=∠3=∠DCB=30. ……………………………………………………4分
在Rt△AEC中,∠AEC=90,
∴ AC=2AE=4
∴EC==.…………………………………………………5分
∴ BC= BE+EC=2+. …………………………………………………6分
23、解:(1) 一次函数解析式 ………………………2分
反比例函数解析式 ………………………4分
(2) ………………………6分
24、解 (1)
(2) AP ∥ DC 理由略
(3) 菱形 P(2,2) 梯形 P1(1,4) P 2(1,4)
25、⑴EAF、△EAF、GF.
⑵DE+BF=EF,理由如下:
假设∠BAD的度数为,将△ADE绕点A顺时针旋转得到△ABG,
此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF= , ∴∠2+∠3=∠BAD-∠EAF=.
∵∠1=∠2, ∴∠1+∠3=.
即∠GAF=∠EAF.
又AG=AE,AF=AF,
∴△GAF≌△EAF.
∴GF=EF,
又∵GF=BG+BF=DE+BF , ∴DE+BF=EF.
26、 解:(1)∵ABCD是矩形,
∴AM∥DN.
∴∠KNM=∠1.
∵∠1=70°,
∴∠KNM=∠KMN=70°,
∴∠MKN=40°.
(2)不能.
过M点作ME⊥DN,垂足为E,则ME=AD=1.
∵∠KNM=∠KMN,
∴MK=NK,
又MK≥ME,
∴NK≥1.
∴△MNK的面积=NK ME≥.
∴△MNK的面积不可能小于.
(3)分两种情况:
情况一:将矩形纸片对折,使点B与D重合,此时点K也与D重合.
MK=MD=x,则AM=5﹣x.
由勾股定理得12+(5﹣x)2=x2,
解得x=2.6.
∴MD=ND=2.6.
S△MNK=S△MND==1.3.
情况二:将矩形纸片沿对角线AC对折,此时折痕即为AC.
MK=AK=CK=x,则DK=5﹣x.
同理可得MK=NK=2.6.
∵MD=1
∴S△MNK==1.3.
△MNK的面积最大值为1.3.
O
C
B
D
P
E
x
A
y
③
②
①
②解的图
2010年11月5日初二数学 试卷第 6 页 共 6 页
初二数学试卷 第 1 页 共6页
初 二 数 学
试卷说明:1、本试卷共6页,计四类大题,26道小题;2、本次考试卷面分值100分,考试时间为90分钟;3、认真审题,所有试题全部在卷面作答。
一、选择题(每小题的四个选项中,只有一个是符合题目要求的.请将你认为符合要求的一项的序号填在题中的括号内.每小题3分,共30分)
1. 下列二次根式中,属于最简二次根式的是( ).
A. B. C. D.
2. 已知反比例函数y =的图象在第二、四象限,则m的取值范围是( ).
A. m≥5 B. m>5 C. m≤5 D. m<5
3. 下列各式中,计算正确的是( ).
A. B.
C. D.
4. 直角三角形的两条直角边的长分别为5,12,则斜边上的中线为( ).
A. cm B. 13cm C. 6cm D. cm
5. 下列各组数中, 能成为直角三角形的三条边长的是 ( ).
A.9, 80, 81 B. 10,24,25 C. 9 ,15,20 D. 8,15,17
6. 已知一次函数y1=kx+b与反比例函数y2=在同一直角坐标系中的图象如图所示,
则当y1<y2时,x的取值范围是( )
A.x<﹣1或0<x<3 B.﹣1<x<0或x>3
C.﹣1<x<0 D.x>3
7. 已知正比例函数的图象与反比例函数的图象的一个交点坐标是,则另一个交点的坐标是( ).
A. B. C. D.
8. 如图,在□ABCD中,已知AD=8cm,AB=6cm,
DE平分∠ADC交BC边于点E,则BE等于( ).
A.2cm B.4cm C.6cm D.8cm
9. 如下图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
A.14 B.16 C.20 D.28
10.如图,四边形ABCD中,AC=a,BD=b,且AC丄BD,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是
④四边形AnBnCnDn的面积是.
A、①② B、②③ C、②③④ D、①②③④
(第9题) (第10题)
二.填空题(请将正确答案填在题中的横线上.每空3分,共24分)
11. 使式子有意义的条件是 .
12. 若,则 .
13. 梯形的上底长为6cm,过上底的一顶点引一腰的平行线,交下底所构成的三角形周长为21cm,那么该梯形的周长是 .
14. 如下图,□ ABCD的对角线相交于点O,两条对角线的和为18,AD的长为5,则OBC的周长为 ___________.
15. 如下图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长
是 .
16.把一张矩形纸片ABCD按如下图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数是 °.
(14题图) (15题图) (16题图)
17.如图,点A在双曲线上,点B在双曲线上,
且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,
则它的面积为 .
18.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是 .
三.计算下列各题(每小题5分,共10分)
19.20. 解: 解:
四.解答题(每小题6分,共36分)
21.如图,已知□ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.
求证:四边形AECF是平行四边形.
证明:
22..如图,梯形ABCD中, AD//BC, ∠ABC=45 , ∠ADC=120 ,
AD=DC,AB=,求BC的长.
23.已知一次函数的图象与反比例函数的图象交于点、.(1)求一次函数和反比例函数的解析式;(2)求△MON的面积.
(1)解:
(2)解:
24.如图,在平面直角坐标系中,双曲线y= 过点A(-4,1),点P是双曲线上一动点(不与A重合),过点A和P分别向两坐标轴作垂线,垂足分别为B、C和D、E.
(1)求k、S△ADC及S△PDC的值;
(2)判断AP和DC的位置关系,并说明理由;
(3)若点P在双曲线上运动时,探索以A、P、C、D四点为顶点的四边形能否成为菱形和等腰梯形?若能,请直接写出所有满足条件的点P的坐标;若不能,请说明理由.
25.如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连结EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° , ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF,
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
⑵方法迁移:
如图②,将沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
26.如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)若∠1=70°,求∠MKN的度数;
(2)△MNK的面积能否小于?若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.
2011—2012学年度第二学期北京市第三十五中学期中质量检测
初 二 数 学 答 案
一 、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B D D B A A D C
二、填空题
11 12 13 14 15 16 17 18
14 24 60° 2 15°或75°
三、解答题
19、 原式= 20、原式=
21、 略
22、 解:解:如图,过A作AE⊥BC于E, 连接AC.
∴ ∠AEB=∠AEC=90.
∵ ∠ABC=45,AB=,
∴ AE=BE =2. ………………2分
∵ AD//BC, ∠ADC=120,
∴ ∠1=∠2, ∠D+∠DCB=180.
∴ ∠DCB=60. ………………………………………………………………………3分
∵ AD=DC,
∴ ∠1=∠3.
∴ ∠2=∠3=∠DCB=30. ……………………………………………………4分
在Rt△AEC中,∠AEC=90,
∴ AC=2AE=4
∴EC==.…………………………………………………5分
∴ BC= BE+EC=2+. …………………………………………………6分
23、解:(1) 一次函数解析式 ………………………2分
反比例函数解析式 ………………………4分
(2) ………………………6分
24、解 (1)
(2) AP ∥ DC 理由略
(3) 菱形 P(2,2) 梯形 P1(1,4) P 2(1,4)
25、⑴EAF、△EAF、GF.
⑵DE+BF=EF,理由如下:
假设∠BAD的度数为,将△ADE绕点A顺时针旋转得到△ABG,
此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF= , ∴∠2+∠3=∠BAD-∠EAF=.
∵∠1=∠2, ∴∠1+∠3=.
即∠GAF=∠EAF.
又AG=AE,AF=AF,
∴△GAF≌△EAF.
∴GF=EF,
又∵GF=BG+BF=DE+BF , ∴DE+BF=EF.
26、 解:(1)∵ABCD是矩形,
∴AM∥DN.
∴∠KNM=∠1.
∵∠1=70°,
∴∠KNM=∠KMN=70°,
∴∠MKN=40°.
(2)不能.
过M点作ME⊥DN,垂足为E,则ME=AD=1.
∵∠KNM=∠KMN,
∴MK=NK,
又MK≥ME,
∴NK≥1.
∴△MNK的面积=NK ME≥.
∴△MNK的面积不可能小于.
(3)分两种情况:
情况一:将矩形纸片对折,使点B与D重合,此时点K也与D重合.
MK=MD=x,则AM=5﹣x.
由勾股定理得12+(5﹣x)2=x2,
解得x=2.6.
∴MD=ND=2.6.
S△MNK=S△MND==1.3.
情况二:将矩形纸片沿对角线AC对折,此时折痕即为AC.
MK=AK=CK=x,则DK=5﹣x.
同理可得MK=NK=2.6.
∵MD=1
∴S△MNK==1.3.
△MNK的面积最大值为1.3.
O
C
B
D
P
E
x
A
y
③
②
①
②解的图
2010年11月5日初二数学 试卷第 6 页 共 6 页
初二数学试卷 第 1 页 共6页
同课章节目录
