2021-2022学年北师大版七年级数学上册第一章丰富的图形世界单元测试(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册第一章丰富的图形世界单元测试(Word版,附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 230.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览

文档简介
丰富的图形世界
单元测试
满分:100分,限时:60分钟
一、选择题(每题3分,共30分)
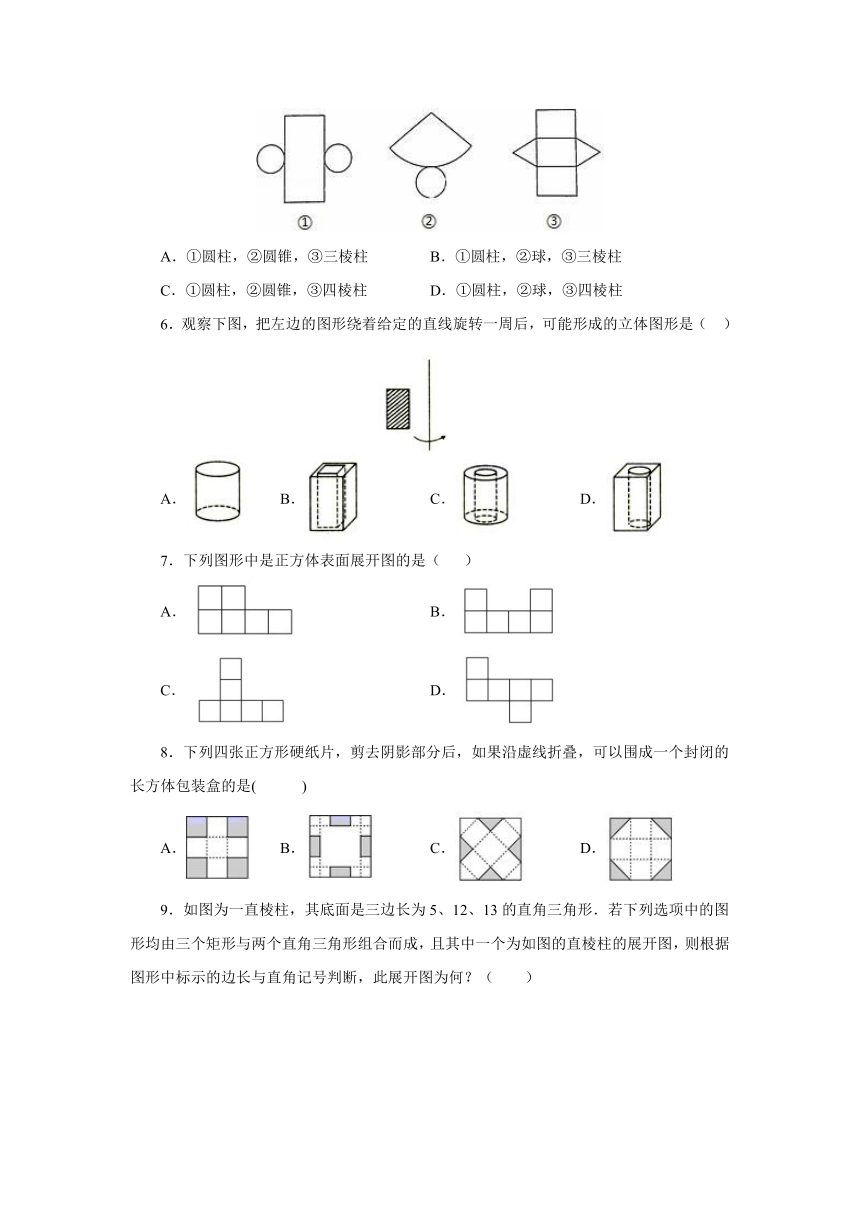
1.下面几何体的截面图不可能是圆的是
(
)
A.圆柱
B.圆锥
C.球
D.棱柱
2.下列图形中,棱锥是( )
A.
B.
C.
D.
3.附图的长方体与下列选项中的立体图形均是由边长为1公分的小正方体紧密堆砌而成.若下列有一立体图形的表面积与附图的表面积相同,则此图形为何?(???
)
A.
B.
C.
D.
4.由4个相同的小正方体搭建了一个积木,从不同方向看积木,所得到的图形如图所示,则这个积木可能是(
)
A.A
B.B
C.C
D.D
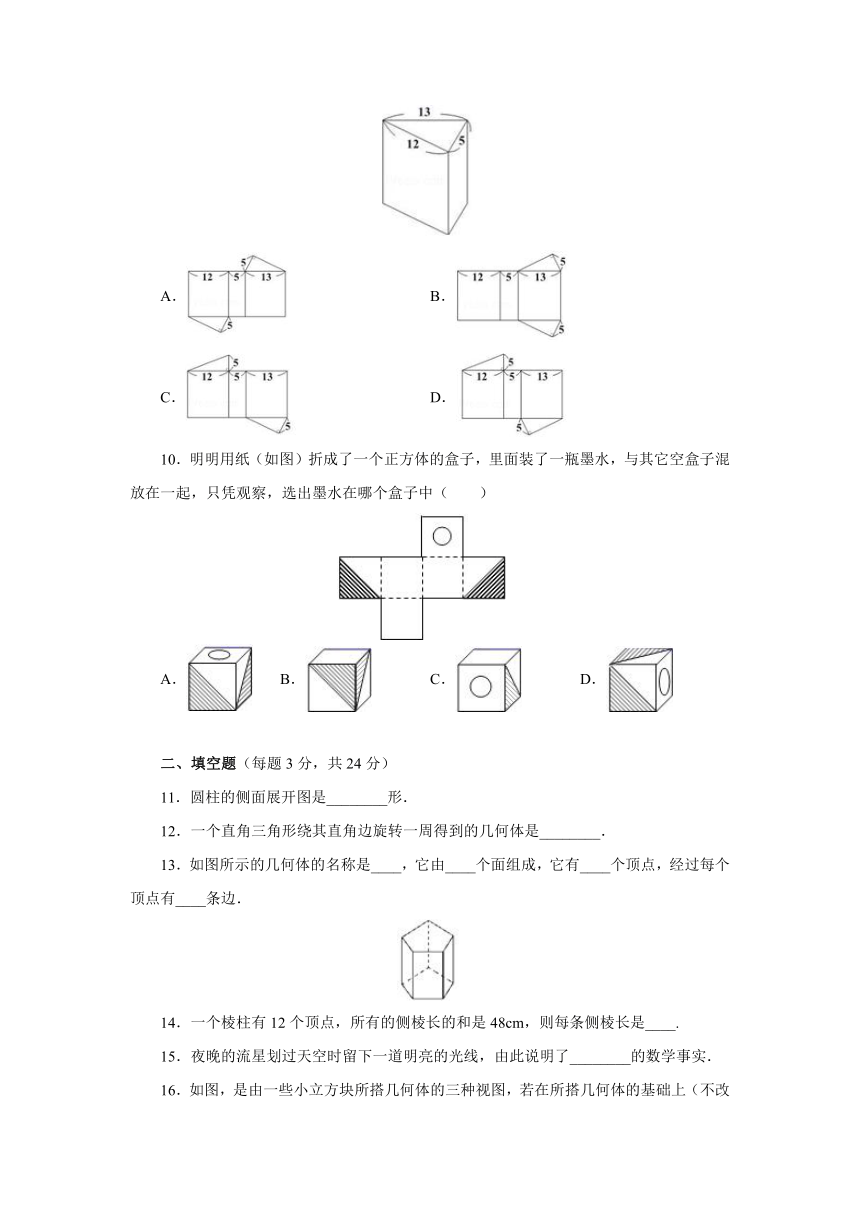
5.三个立体图形的展开图如图①②③所示,则相应的立体图形是(
)
A.①圆柱,②圆锥,③三棱柱
B.①圆柱,②球,③三棱柱
C.①圆柱,②圆锥,③四棱柱
D.①圆柱,②球,③四棱柱
6.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(?
?)
A.
B.
C.
D.
7.下列图形中是正方体表面展开图的是(
)
A.
B.
C.
D.
8.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是(
)
A.
B.
C.
D.
9.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A.
B.
C.
D.
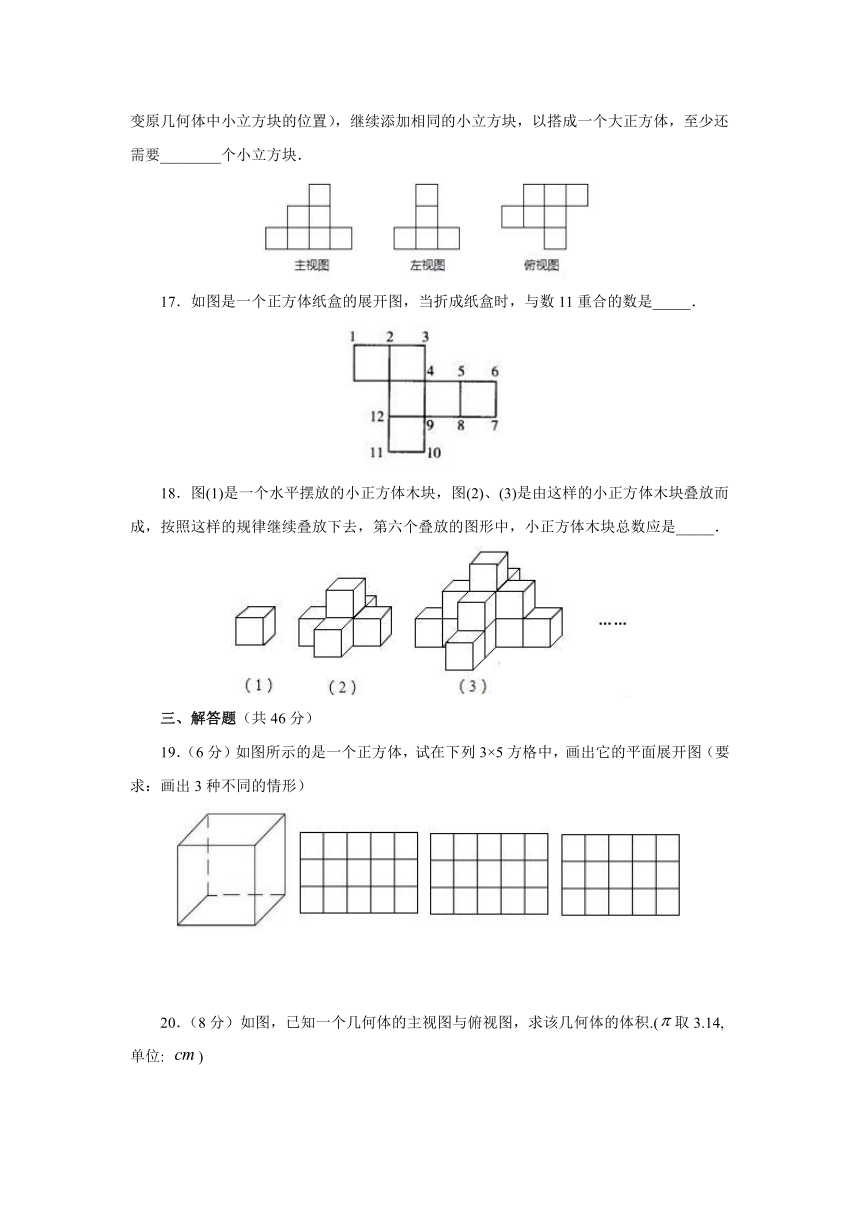
10.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
?
A.?
B.?
C.?
D.?
二、填空题(每题3分,共24分)
11.圆柱的侧面展开图是________形.
12.一个直角三角形绕其直角边旋转一周得到的几何体是________.
13.如图所示的几何体的名称是____,它由____个面组成,它有____个顶点,经过每个顶点有____条边.
14.一个棱柱有12个顶点,所有的侧棱长的和是48cm,则每条侧棱长是____.
15.夜晚的流星划过天空时留下一道明亮的光线,由此说明了________的数学事实.
16.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.
17.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是_____.
18.图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,第六个叠放的图形中,小正方体木块总数应是_____.
三、解答题(共46分)
19.(6分)如图所示的是一个正方体,试在下列3×5方格中,画出它的平面展开图(要求:画出3种不同的情形)
20.(8分)如图,已知一个几何体的主视图与俯视图,求该几何体的体积.(取3.14,单位:
)
21.(10分)图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
22.(10分)如图所示是长方体的平面展开图.
(1)将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?
(2)若AG=CK=14
cm,FG=2
cm,LK=5
cm,则该长方体的表面积和体积分别是多少?
23.(12分)仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
⑴填空:
①正四面体的顶点数V=
,面数F=
,棱数E=
.
②正六面体的顶点数V=
,面数F=
,棱数E=
.
③正八面体的顶点数V=
,面数F=
,棱数E=
.
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
参考答案
一、选择题
1--10DCBBA
CDCDB
二、填空题
11.长方
12.圆锥
13.五棱柱
7
10
3
14.8
15.点动成线
16.54
17.1,7
18.66
三、解答题
19.正方体的展开图如图所示,(画出三种即可)
20.解:由几何体的主视图和俯视图,可以想象出该几何体由两部分组成:上部是一个圆柱,底面直径是20cm,高是32cm;下部是一个长方体,长、宽、高分别是30cm,25cm,40cm,所以该几何体的体积为.
21.解:如图所示:
22.解:(1)与点N重合的点有H,J两个.
(2)∵AG=CK=14cm,LK=5cm,
∴CL=CK-LK=14-5=9(cm),
∴长方体的表面积为2×(9×5+2×5+2×9)=146(cm2),长方体的体积为5×9×2=90(cm3).
23.解:⑴①4,4,6;②8,6,12;③6,8,12;
⑵V+F-E=2
⑶解:设面数为F,则20+F-30=2
解得F=12
答:它有12个面.
单元测试
满分:100分,限时:60分钟
一、选择题(每题3分,共30分)
1.下面几何体的截面图不可能是圆的是
(
)
A.圆柱
B.圆锥
C.球
D.棱柱
2.下列图形中,棱锥是( )
A.
B.
C.
D.
3.附图的长方体与下列选项中的立体图形均是由边长为1公分的小正方体紧密堆砌而成.若下列有一立体图形的表面积与附图的表面积相同,则此图形为何?(???
)
A.
B.
C.
D.
4.由4个相同的小正方体搭建了一个积木,从不同方向看积木,所得到的图形如图所示,则这个积木可能是(
)
A.A
B.B
C.C
D.D
5.三个立体图形的展开图如图①②③所示,则相应的立体图形是(
)
A.①圆柱,②圆锥,③三棱柱
B.①圆柱,②球,③三棱柱
C.①圆柱,②圆锥,③四棱柱
D.①圆柱,②球,③四棱柱
6.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(?
?)
A.
B.
C.
D.
7.下列图形中是正方体表面展开图的是(
)
A.
B.
C.
D.
8.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是(
)
A.
B.
C.
D.
9.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A.
B.
C.
D.
10.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
?
A.?
B.?
C.?
D.?
二、填空题(每题3分,共24分)
11.圆柱的侧面展开图是________形.
12.一个直角三角形绕其直角边旋转一周得到的几何体是________.
13.如图所示的几何体的名称是____,它由____个面组成,它有____个顶点,经过每个顶点有____条边.
14.一个棱柱有12个顶点,所有的侧棱长的和是48cm,则每条侧棱长是____.
15.夜晚的流星划过天空时留下一道明亮的光线,由此说明了________的数学事实.
16.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.
17.如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是_____.
18.图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,第六个叠放的图形中,小正方体木块总数应是_____.
三、解答题(共46分)
19.(6分)如图所示的是一个正方体,试在下列3×5方格中,画出它的平面展开图(要求:画出3种不同的情形)
20.(8分)如图,已知一个几何体的主视图与俯视图,求该几何体的体积.(取3.14,单位:
)
21.(10分)图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
22.(10分)如图所示是长方体的平面展开图.
(1)将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?
(2)若AG=CK=14
cm,FG=2
cm,LK=5
cm,则该长方体的表面积和体积分别是多少?
23.(12分)仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
⑴填空:
①正四面体的顶点数V=
,面数F=
,棱数E=
.
②正六面体的顶点数V=
,面数F=
,棱数E=
.
③正八面体的顶点数V=
,面数F=
,棱数E=
.
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
参考答案
一、选择题
1--10DCBBA
CDCDB
二、填空题
11.长方
12.圆锥
13.五棱柱
7
10
3
14.8
15.点动成线
16.54
17.1,7
18.66
三、解答题
19.正方体的展开图如图所示,(画出三种即可)
20.解:由几何体的主视图和俯视图,可以想象出该几何体由两部分组成:上部是一个圆柱,底面直径是20cm,高是32cm;下部是一个长方体,长、宽、高分别是30cm,25cm,40cm,所以该几何体的体积为.
21.解:如图所示:
22.解:(1)与点N重合的点有H,J两个.
(2)∵AG=CK=14cm,LK=5cm,
∴CL=CK-LK=14-5=9(cm),
∴长方体的表面积为2×(9×5+2×5+2×9)=146(cm2),长方体的体积为5×9×2=90(cm3).
23.解:⑴①4,4,6;②8,6,12;③6,8,12;
⑵V+F-E=2
⑶解:设面数为F,则20+F-30=2
解得F=12
答:它有12个面.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
