《第2章一元二次方程》单元综合基础达标训练(附答案)2021年暑假自主学习九年级数学北师大版上册(word版含解析)
文档属性
| 名称 | 《第2章一元二次方程》单元综合基础达标训练(附答案)2021年暑假自主学习九年级数学北师大版上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 103.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 00:00:00 | ||
图片预览



文档简介
2021年北师大版九年级数学上册《第2章一元二次方程》暑假自主学习单元综合
基础达标训练(附答案)
1.若一元二次方程ax2﹣(b﹣1)x﹣2021=0有一根为x=﹣1,则a+b的值 .
2.若m是方程x2﹣2x﹣1=0的解,则代数式2m2﹣4m+2021的值为 .
3.在小华的某个微信群中,若每人给其他成员都发一个红包,该微信群共发了90个红包,那么这个微信群共有 人.
4.已知α,β方程x2+2x﹣5=0的两根,那么α2+3α+β的值是 .
5.已知x1、x2是方程x2﹣3x﹣1=0的根,则式子x12﹣2x1+x2的值为 .
6.一个等腰三角形的腰和底边长分别是方程x2﹣8x+12=0的两根,则该等腰三角形的周长是 .
7.将一元二次方程x2﹣8x﹣5=0化成(x+a)2=b(a、b为常数)的形式,则a、b的值分别是 .
8.若m是方程x2﹣x﹣5=0的一个实数根,则代数式(m2﹣m)(m﹣+1)的值为 .
9.关于x的一元二次方程kx2﹣(2k+1)x+k=0总有两个实数根,则常数k的取值范围是 .
10.方程a(x+m)2+b=0的解是x1=﹣2,x2=1,则方程a(x+m+2)2+b=0的解是 .
11.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 cm.
12.已知?x1,?x2是关于x的一元二次方程?x2+2x+k﹣1=0的两个实数根,且?,则k的值为 .
13.已知实数x、y满足(x2+y2+1)(x2+y2﹣3)=0,则x2+y2= .
14.已知a是方程x2﹣2021x+1=0的一个根,则a3﹣2021a2﹣= .
15.已知方程x2+4x﹣2m=0的一个根比另一个根小4,求这两个根和m的值.
16.已知关于x的一元二次方程x2+(2m+1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
17.已知关于x的方程x2+(2m﹣1)x+m2﹣1=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)若x1,x2满足x12+x22=x1x2+16,求实数m的值.
18.已知关于x的一元二次方程x2﹣4x+2m+3=0有两个不相等的实数根x1,x2.
(1)求m的取值范围;
(2)若,m为整数,求m的值.
19.某种肺炎病毒在M国爆发,经世卫组织研究发现:病毒有极强的传染性.在调查某工厂的疫情时,发现最初只有1位出差回来的病毒携带者,在召开工厂车间组长会议时发生了第一轮传染,开完会后所有人都回到各自车间工作又发生了第二轮传染,这时全厂一共有196人检测出携带病毒.假如每个病毒携带者每次传染人数都相同,求每个病毒携带者每次传染多少人?
20.2020年上半年受到新冠状肺炎疫情的影响,汽车销售行业处于不景气状态,2020年下半年合肥某汽车销售公司推行了一种新型低能耗汽车,于2020年10月份销售该型号汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆.
(1)求11月份和12月份的平均增长率;
(2)该型号汽车每辆的进价为10万元,且销售a辆汽车,汽车厂队销售公司每辆返利0.03a万元,该公司这种型号汽车的售价为11万元/辆,若使2021年1月份每辆汽车盈利不低于2.6万元,那么该公司1月份至少需要销售该型号汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
21.阿里巴巴电商扶贫对某贫困地区一种特色农产品进行网上销售,按原价每件300元出售,一个月可卖出100件,通过市场调查发现,售价每件每降低10元,月销售件数增加20件.已知该农产品的成本是每件200元,在保持月利润不变的情况下,尽快销售完毕,则售价应定为多少元?
22.某商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
①若降价6元时,则平均每天销售数量为多少件?
②当每件商品降价多少元时,该商店每天销售利润为1200元?
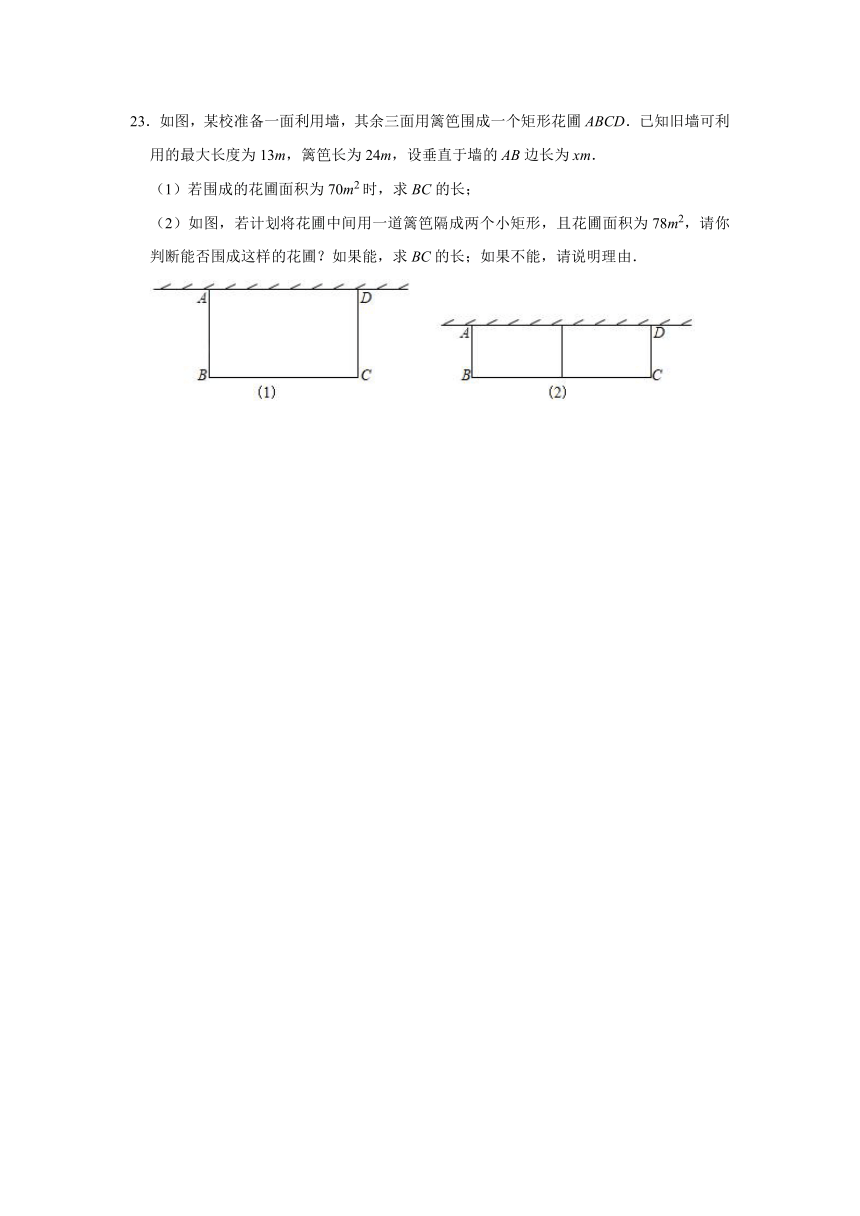
23.如图,某校准备一面利用墙,其余三面用篱笆围成一个矩形花圃ABCD.已知旧墙可利用的最大长度为13m,篱笆长为24m,设垂直于墙的AB边长为xm.
(1)若围成的花圃面积为70m2时,求BC的长;
(2)如图,若计划将花圃中间用一道篱笆隔成两个小矩形,且花圃面积为78m2,请你判断能否围成这样的花圃?如果能,求BC的长;如果不能,请说明理由.
参考答案
1.解:把x=﹣1代入ax2﹣(b﹣1)x﹣2021=0得a+(b﹣1)﹣2021=0,
所以a+b=2022.
故答案为2022.
2.解:∵m是方程x2﹣2x﹣1=0的解,
∴m2﹣2m﹣1=0,
∴m2﹣2m=1,
∴2m2﹣4m+2021=2(m2﹣2m)+2021=2×1+2021=2023.
故答案为:2023.
3.解:设这个微信群共有x人,则每人需发(x﹣1)个红包,
依题意得:x(x﹣1)=90,
整理得:x2﹣x﹣90=0,
解得:x1=10,x2=﹣9(不合题意,舍去).
故答案为:10.
4.解:∵α,β方程x2+2x﹣5=0的两根,
∴α2+2α﹣5=0,α+β=﹣2,
∴α2+2α=5,
∴α2+3α+β=α2+2α+α+β=5﹣2=3.
故答案为:3.
5.解:∵x1、x2是方程x2﹣3x﹣1=0的根,
∴x1+x2=3,x12﹣3x1﹣1=0,
∴x12﹣3x1=1,
∴x12﹣2x1+x2=x12﹣3x1+x1+x2=1+3=4.
故答案为:4.
6.解:∵x2﹣8x+12=0,
∴(x﹣2)(x﹣6)=0,
∴x1=2,x2=6.
∵三角形是等腰三角形,必须满足三角形三边的关系,
∴腰长是6,底边是2,
周长为:6+6+2=14,
故答案为:14.
7.解:x2﹣8x﹣5=0,
x2﹣8x=5,
x2﹣8x+42=5+42,
(x﹣4)2=21,
所以a=﹣4,b=21,
故答案为:﹣4,21.
8.解:∵m是方程x2﹣x﹣5=0的一个实数根,
∴m2﹣m=5,
m﹣1﹣=0,
故m﹣=1,
则(m2﹣m)(m﹣+1)
=5×2
=10.
故答案为:10.
9.解:∵△=b2﹣4ac
=[﹣(2k+1)]2﹣4k×k≥0,
解得k≥﹣,
∵二次项系数k≠0,
∴k≥﹣且k≠0.
故答案为:k≥﹣且k≠0.
10.解:∵方程a(x+m)2+b=0的解是x1=﹣2,x2=1,
∴方程a(x+m+2)2+b=0的两个解是x3=﹣2﹣2=﹣4,x4=1﹣2=﹣1,
故答案为:x3=﹣4,x4=﹣1.
11.解:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x﹣2=0或x﹣1=0,
∴x1=2,x2=1,
当x=2时,三角形三边为3,2,2,则三角形的周长=3+2+2=7(cm);
当x=1时,由于1+2=3,不符合三角形三边的关系,舍去.
所以这个三角形的周长为7cm,
故答案为7.
12.解:根据题意得:x1+x2=﹣2,x1x2=k﹣1,
x12+x22﹣x1x2
=(x1+x2)2﹣3x1x2
=4﹣3(k﹣1)
=13,
∴k=﹣2,
经检验,k=﹣2符合题意,
故答案为:﹣2.
13.解:设x2+y2=a,
则(a+1)(a﹣3)=0,
解得a=﹣1或a=3,
当a=﹣1时,x2+y2=﹣1,不合题意,舍去;
故x2+y2=3,
故答案为:3.
14.解:∵a是方程x2﹣2021x+1=0的一个根,
∴x2﹣2021x+1=0,即a2+1=2021a,a2﹣2021a=﹣1,
则a3﹣2021a2﹣=a(a2﹣2021a)﹣=﹣a﹣=﹣=﹣=﹣2021.
故答案是:﹣2021.
二.解答题(共9小题)
15.解:设α、β是方程x2+4x﹣2m=0的两个根,
∵方程x2+4x﹣2m=0的一个根比另一个根小4,
∴α+β=﹣4,α?β=﹣2m,α=β﹣4,
解得:α=﹣4,β=0,m=0.
故此方程的两个根为﹣4和0,m的值为0.
16.解:(1)根据题意得△=(2m+1)2﹣4m2≥0,
解得m≥﹣;
(2)根据题意得x1+x2=﹣(2m+1),x1x2=m2,
∵x12﹣x22=0,
∴(x1+x2)(x1﹣x2)=0,
∴x1+x2=0或x1﹣x2=0,
即﹣(2m+1)=0或△=(2m+1)2﹣4m2=0,
解得m=﹣或m=﹣,
而m≥﹣,
∴m的值为﹣.
17.解:(1)∵关于x的方程x2+(2m﹣1)x+m2﹣1=0有两个实数根x1和x2.
∴△=(2m﹣1)2﹣4(m2﹣1)=﹣4m+5≥0,
∴m≤.
(2)∵x1+x2=1﹣2m,x1?x2=m2﹣1,x12+x22=x1x2+16,
∴(1﹣2m)2=3(m2﹣1)+16,即m2﹣4m﹣12=0,
解得:m=6或m=﹣2,
∵m≤,
∴m=﹣2.
18.解:(1)由题意可得,△=(﹣4)2﹣4(2m+3)=4﹣8m,
∵方程有两个不相等的实数根,
∴△=4﹣8m>0.
解得m<;
(2)由根与系数的关系可得x1+x2=4,x1x2=2m+3,
∵,
∴(x1+x2)2﹣3x1x2≤13,
即42﹣3(2m+3)≤13,
解得m≥﹣1,
由(1)可得﹣1≤m<,
又∵m为整数,
∴m=﹣1或m=0.
19.解:设每个病毒携带者每次传染x人,
依题意得:(1+x)2=196,
解得:x1=13,x2=﹣15(不合题意,舍去).
答:每个病毒携带者每次传染13人.
20.解:(1)设11月份和12月份的平均增长率为x,
依题意得:20(1+x)?=45,
解得:x1=0.5=50%,x2=﹣2.5(不合题意,舍去).
答:11月份和12月份的平均增长率为50%.
(2)依题意得:11﹣10+0.03a≥2.6,
解得:a≥53.
又∵a为整数,
∴a可取的最小值为54,
∴此时总盈利为54×(11﹣10+0.03×54)=141.48(万元).
答:该公司1月份至少需要销售该型号汽车54辆,此时总盈利至少是141.48万元.
21.解:设售价应定为x元,则每件的利润为(x﹣200)元,月销售量为100+=(700﹣2x)件,
依题意,得:(x﹣200)(700﹣2x)=(300﹣200)×100,
整理,得:x2﹣550x+75000=0,
解得:x1=250,x2=300(舍去).
答:售价应定为250元.
22.解:①根据题意得:
若降价6元,则多售出12件,
平均每天销售数量为:12+20=32(件),
答:平均每天销售数量为32件;
②设每件商品降价x元,
根据题意得:
(40﹣x)(20+2x)=1200,
解得:x1=10,x2=20,
40﹣10=30>25,(符合题意),
40﹣20=20<25,(舍去),
答:当每件商品降价10元时,该商店每天销售利润为1200元.
23.(1)解:根据题意得:BC=(24﹣2x)m,
则(24﹣2x)x=70,
解得:x1=5,x2=7,
当x1=5时,BC=14x2=7时,BC=10,
墙可利用的最大长度为13m,BC=14舍去.
答:BC的长为10m.
(2)解:不能围成这样的花圃.理由如下:
依题意可知:(24﹣3x)x=78,
即x2﹣8x+26=0,△=82﹣4×1×26=﹣40<0,
所以方程无实数根,
答:不能围成这样的花圃
基础达标训练(附答案)
1.若一元二次方程ax2﹣(b﹣1)x﹣2021=0有一根为x=﹣1,则a+b的值 .
2.若m是方程x2﹣2x﹣1=0的解,则代数式2m2﹣4m+2021的值为 .
3.在小华的某个微信群中,若每人给其他成员都发一个红包,该微信群共发了90个红包,那么这个微信群共有 人.
4.已知α,β方程x2+2x﹣5=0的两根,那么α2+3α+β的值是 .
5.已知x1、x2是方程x2﹣3x﹣1=0的根,则式子x12﹣2x1+x2的值为 .
6.一个等腰三角形的腰和底边长分别是方程x2﹣8x+12=0的两根,则该等腰三角形的周长是 .
7.将一元二次方程x2﹣8x﹣5=0化成(x+a)2=b(a、b为常数)的形式,则a、b的值分别是 .
8.若m是方程x2﹣x﹣5=0的一个实数根,则代数式(m2﹣m)(m﹣+1)的值为 .
9.关于x的一元二次方程kx2﹣(2k+1)x+k=0总有两个实数根,则常数k的取值范围是 .
10.方程a(x+m)2+b=0的解是x1=﹣2,x2=1,则方程a(x+m+2)2+b=0的解是 .
11.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 cm.
12.已知?x1,?x2是关于x的一元二次方程?x2+2x+k﹣1=0的两个实数根,且?,则k的值为 .
13.已知实数x、y满足(x2+y2+1)(x2+y2﹣3)=0,则x2+y2= .
14.已知a是方程x2﹣2021x+1=0的一个根,则a3﹣2021a2﹣= .
15.已知方程x2+4x﹣2m=0的一个根比另一个根小4,求这两个根和m的值.
16.已知关于x的一元二次方程x2+(2m+1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
17.已知关于x的方程x2+(2m﹣1)x+m2﹣1=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)若x1,x2满足x12+x22=x1x2+16,求实数m的值.
18.已知关于x的一元二次方程x2﹣4x+2m+3=0有两个不相等的实数根x1,x2.
(1)求m的取值范围;
(2)若,m为整数,求m的值.
19.某种肺炎病毒在M国爆发,经世卫组织研究发现:病毒有极强的传染性.在调查某工厂的疫情时,发现最初只有1位出差回来的病毒携带者,在召开工厂车间组长会议时发生了第一轮传染,开完会后所有人都回到各自车间工作又发生了第二轮传染,这时全厂一共有196人检测出携带病毒.假如每个病毒携带者每次传染人数都相同,求每个病毒携带者每次传染多少人?
20.2020年上半年受到新冠状肺炎疫情的影响,汽车销售行业处于不景气状态,2020年下半年合肥某汽车销售公司推行了一种新型低能耗汽车,于2020年10月份销售该型号汽车20辆,由于该型号汽车经济适用性强,销量快速上升,12月份该公司销售该型号汽车达45辆.
(1)求11月份和12月份的平均增长率;
(2)该型号汽车每辆的进价为10万元,且销售a辆汽车,汽车厂队销售公司每辆返利0.03a万元,该公司这种型号汽车的售价为11万元/辆,若使2021年1月份每辆汽车盈利不低于2.6万元,那么该公司1月份至少需要销售该型号汽车多少辆?此时总盈利至少是多少万元?(盈利=销售利润+返利)
21.阿里巴巴电商扶贫对某贫困地区一种特色农产品进行网上销售,按原价每件300元出售,一个月可卖出100件,通过市场调查发现,售价每件每降低10元,月销售件数增加20件.已知该农产品的成本是每件200元,在保持月利润不变的情况下,尽快销售完毕,则售价应定为多少元?
22.某商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
①若降价6元时,则平均每天销售数量为多少件?
②当每件商品降价多少元时,该商店每天销售利润为1200元?
23.如图,某校准备一面利用墙,其余三面用篱笆围成一个矩形花圃ABCD.已知旧墙可利用的最大长度为13m,篱笆长为24m,设垂直于墙的AB边长为xm.
(1)若围成的花圃面积为70m2时,求BC的长;
(2)如图,若计划将花圃中间用一道篱笆隔成两个小矩形,且花圃面积为78m2,请你判断能否围成这样的花圃?如果能,求BC的长;如果不能,请说明理由.
参考答案
1.解:把x=﹣1代入ax2﹣(b﹣1)x﹣2021=0得a+(b﹣1)﹣2021=0,
所以a+b=2022.
故答案为2022.
2.解:∵m是方程x2﹣2x﹣1=0的解,
∴m2﹣2m﹣1=0,
∴m2﹣2m=1,
∴2m2﹣4m+2021=2(m2﹣2m)+2021=2×1+2021=2023.
故答案为:2023.
3.解:设这个微信群共有x人,则每人需发(x﹣1)个红包,
依题意得:x(x﹣1)=90,
整理得:x2﹣x﹣90=0,
解得:x1=10,x2=﹣9(不合题意,舍去).
故答案为:10.
4.解:∵α,β方程x2+2x﹣5=0的两根,
∴α2+2α﹣5=0,α+β=﹣2,
∴α2+2α=5,
∴α2+3α+β=α2+2α+α+β=5﹣2=3.
故答案为:3.
5.解:∵x1、x2是方程x2﹣3x﹣1=0的根,
∴x1+x2=3,x12﹣3x1﹣1=0,
∴x12﹣3x1=1,
∴x12﹣2x1+x2=x12﹣3x1+x1+x2=1+3=4.
故答案为:4.
6.解:∵x2﹣8x+12=0,
∴(x﹣2)(x﹣6)=0,
∴x1=2,x2=6.
∵三角形是等腰三角形,必须满足三角形三边的关系,
∴腰长是6,底边是2,
周长为:6+6+2=14,
故答案为:14.
7.解:x2﹣8x﹣5=0,
x2﹣8x=5,
x2﹣8x+42=5+42,
(x﹣4)2=21,
所以a=﹣4,b=21,
故答案为:﹣4,21.
8.解:∵m是方程x2﹣x﹣5=0的一个实数根,
∴m2﹣m=5,
m﹣1﹣=0,
故m﹣=1,
则(m2﹣m)(m﹣+1)
=5×2
=10.
故答案为:10.
9.解:∵△=b2﹣4ac
=[﹣(2k+1)]2﹣4k×k≥0,
解得k≥﹣,
∵二次项系数k≠0,
∴k≥﹣且k≠0.
故答案为:k≥﹣且k≠0.
10.解:∵方程a(x+m)2+b=0的解是x1=﹣2,x2=1,
∴方程a(x+m+2)2+b=0的两个解是x3=﹣2﹣2=﹣4,x4=1﹣2=﹣1,
故答案为:x3=﹣4,x4=﹣1.
11.解:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x﹣2=0或x﹣1=0,
∴x1=2,x2=1,
当x=2时,三角形三边为3,2,2,则三角形的周长=3+2+2=7(cm);
当x=1时,由于1+2=3,不符合三角形三边的关系,舍去.
所以这个三角形的周长为7cm,
故答案为7.
12.解:根据题意得:x1+x2=﹣2,x1x2=k﹣1,
x12+x22﹣x1x2
=(x1+x2)2﹣3x1x2
=4﹣3(k﹣1)
=13,
∴k=﹣2,
经检验,k=﹣2符合题意,
故答案为:﹣2.
13.解:设x2+y2=a,
则(a+1)(a﹣3)=0,
解得a=﹣1或a=3,
当a=﹣1时,x2+y2=﹣1,不合题意,舍去;
故x2+y2=3,
故答案为:3.
14.解:∵a是方程x2﹣2021x+1=0的一个根,
∴x2﹣2021x+1=0,即a2+1=2021a,a2﹣2021a=﹣1,
则a3﹣2021a2﹣=a(a2﹣2021a)﹣=﹣a﹣=﹣=﹣=﹣2021.
故答案是:﹣2021.
二.解答题(共9小题)
15.解:设α、β是方程x2+4x﹣2m=0的两个根,
∵方程x2+4x﹣2m=0的一个根比另一个根小4,
∴α+β=﹣4,α?β=﹣2m,α=β﹣4,
解得:α=﹣4,β=0,m=0.
故此方程的两个根为﹣4和0,m的值为0.
16.解:(1)根据题意得△=(2m+1)2﹣4m2≥0,
解得m≥﹣;
(2)根据题意得x1+x2=﹣(2m+1),x1x2=m2,
∵x12﹣x22=0,
∴(x1+x2)(x1﹣x2)=0,
∴x1+x2=0或x1﹣x2=0,
即﹣(2m+1)=0或△=(2m+1)2﹣4m2=0,
解得m=﹣或m=﹣,
而m≥﹣,
∴m的值为﹣.
17.解:(1)∵关于x的方程x2+(2m﹣1)x+m2﹣1=0有两个实数根x1和x2.
∴△=(2m﹣1)2﹣4(m2﹣1)=﹣4m+5≥0,
∴m≤.
(2)∵x1+x2=1﹣2m,x1?x2=m2﹣1,x12+x22=x1x2+16,
∴(1﹣2m)2=3(m2﹣1)+16,即m2﹣4m﹣12=0,
解得:m=6或m=﹣2,
∵m≤,
∴m=﹣2.
18.解:(1)由题意可得,△=(﹣4)2﹣4(2m+3)=4﹣8m,
∵方程有两个不相等的实数根,
∴△=4﹣8m>0.
解得m<;
(2)由根与系数的关系可得x1+x2=4,x1x2=2m+3,
∵,
∴(x1+x2)2﹣3x1x2≤13,
即42﹣3(2m+3)≤13,
解得m≥﹣1,
由(1)可得﹣1≤m<,
又∵m为整数,
∴m=﹣1或m=0.
19.解:设每个病毒携带者每次传染x人,
依题意得:(1+x)2=196,
解得:x1=13,x2=﹣15(不合题意,舍去).
答:每个病毒携带者每次传染13人.
20.解:(1)设11月份和12月份的平均增长率为x,
依题意得:20(1+x)?=45,
解得:x1=0.5=50%,x2=﹣2.5(不合题意,舍去).
答:11月份和12月份的平均增长率为50%.
(2)依题意得:11﹣10+0.03a≥2.6,
解得:a≥53.
又∵a为整数,
∴a可取的最小值为54,
∴此时总盈利为54×(11﹣10+0.03×54)=141.48(万元).
答:该公司1月份至少需要销售该型号汽车54辆,此时总盈利至少是141.48万元.
21.解:设售价应定为x元,则每件的利润为(x﹣200)元,月销售量为100+=(700﹣2x)件,
依题意,得:(x﹣200)(700﹣2x)=(300﹣200)×100,
整理,得:x2﹣550x+75000=0,
解得:x1=250,x2=300(舍去).
答:售价应定为250元.
22.解:①根据题意得:
若降价6元,则多售出12件,
平均每天销售数量为:12+20=32(件),
答:平均每天销售数量为32件;
②设每件商品降价x元,
根据题意得:
(40﹣x)(20+2x)=1200,
解得:x1=10,x2=20,
40﹣10=30>25,(符合题意),
40﹣20=20<25,(舍去),
答:当每件商品降价10元时,该商店每天销售利润为1200元.
23.(1)解:根据题意得:BC=(24﹣2x)m,
则(24﹣2x)x=70,
解得:x1=5,x2=7,
当x1=5时,BC=14x2=7时,BC=10,
墙可利用的最大长度为13m,BC=14舍去.
答:BC的长为10m.
(2)解:不能围成这样的花圃.理由如下:
依题意可知:(24﹣3x)x=78,
即x2﹣8x+26=0,△=82﹣4×1×26=﹣40<0,
所以方程无实数根,
答:不能围成这样的花圃
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
