弧长和扇形的面积
图片预览
文档简介
(共26张PPT)
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
课
题
封
面
教
学
目
标
认识扇形,会计算弧长和扇形的面积,
通过弧长和扇形面积的发现与推导,
培养学生运用已有知识探究问题获得新知的能力。
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
了解扇形的概念,
理解n°的圆心角所对的弧长和扇形面积的计算公式,
并应用这些公式解决相关问题。
学
习
目
标
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
情
境
学
堂
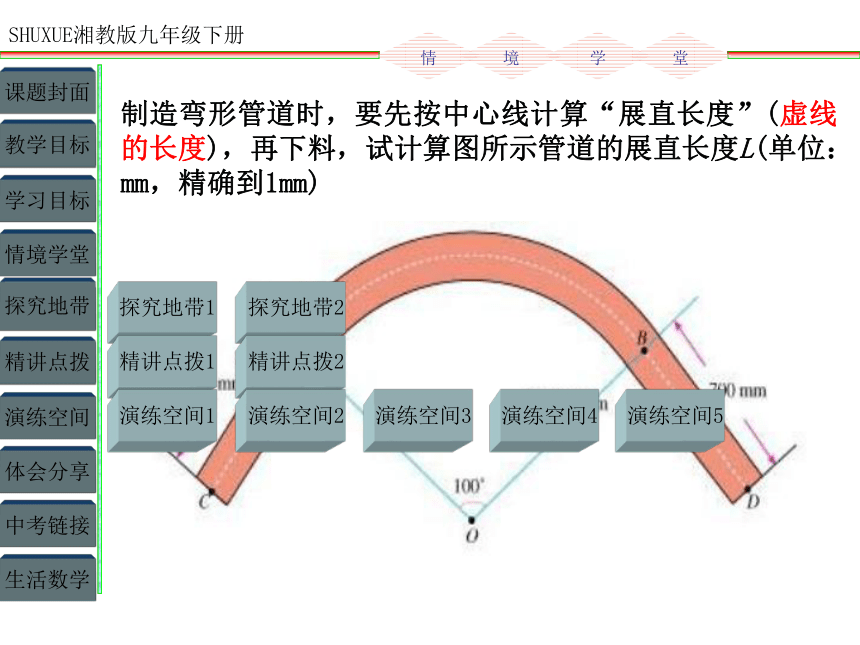
制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
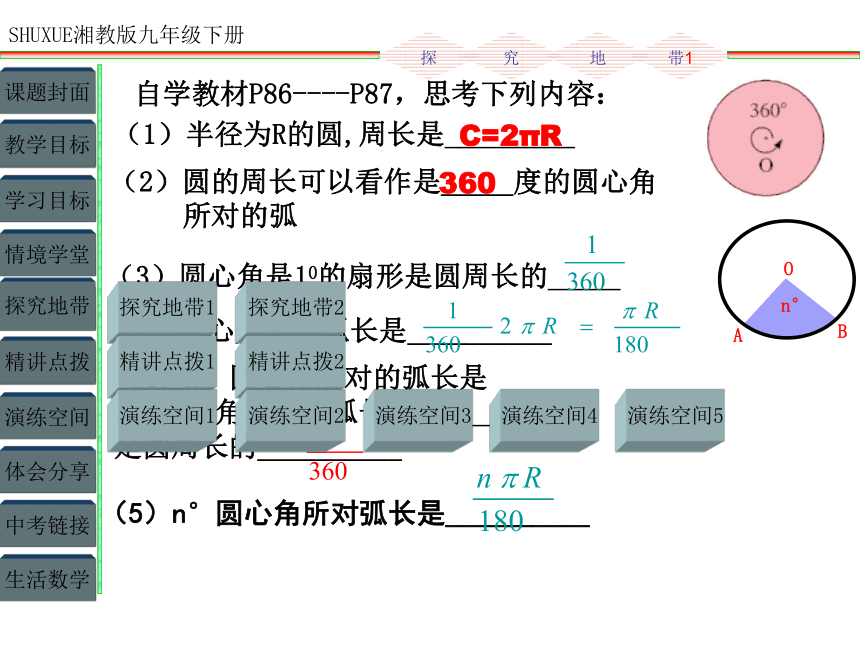
(1)半径为R的圆,周长是_________
C=2πR
(3)圆心角是10的扇形是圆周长的_____
A
B
O
n°
(4)n°圆心角所对的弧长是
1°圆心角所对的弧长的______倍,
是圆周长的__________
n
(5)n°圆心角所对弧长是__________
自学教材P86----P87,思考下列内容:
(2)圆的周长可以看作是_____度的圆心角
所对的弧
360
1°圆心角所对弧长是__________
探
究
地
带1
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
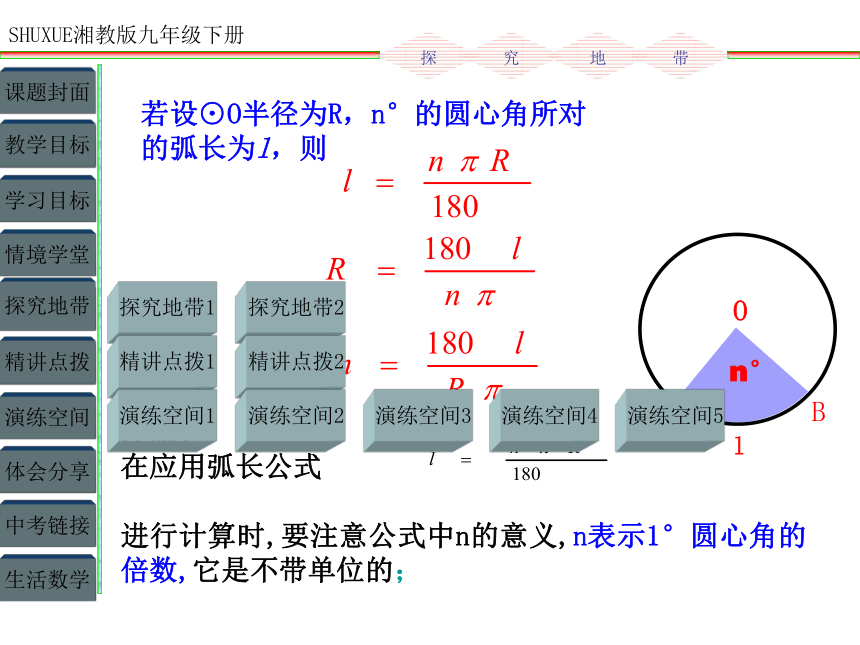
若设⊙O半径为R,n°的圆心角所对
的弧长为l,则
l
A
B
O
n°
在应用弧长公式
进行计算时,要注意公式中n的意义,n表示1°圆心角的倍数,它是不带单位的;
注意:
探
究
地
带
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
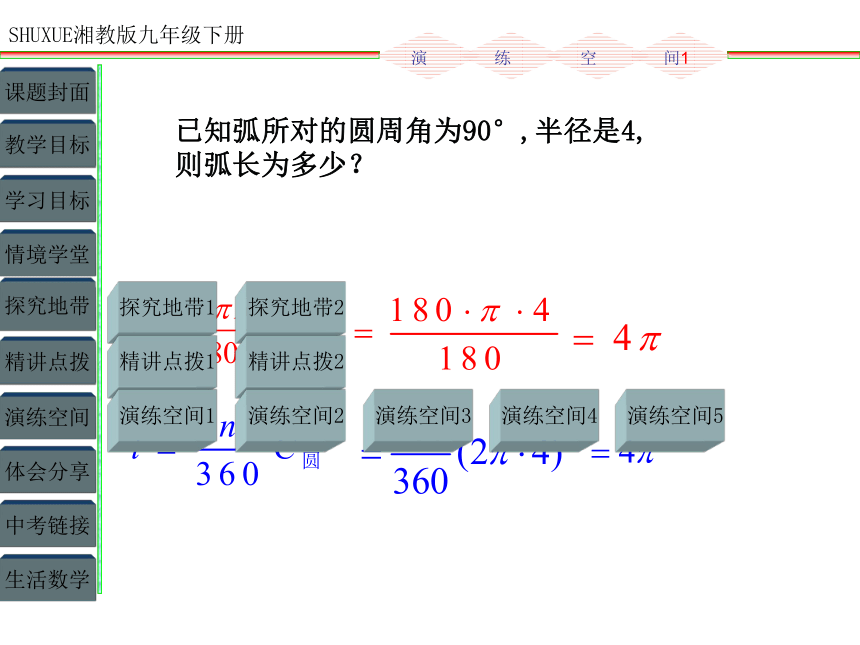
已知弧所对的圆周角为90°,半径是4,
则弧长为多少?
演
练
空
间1
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
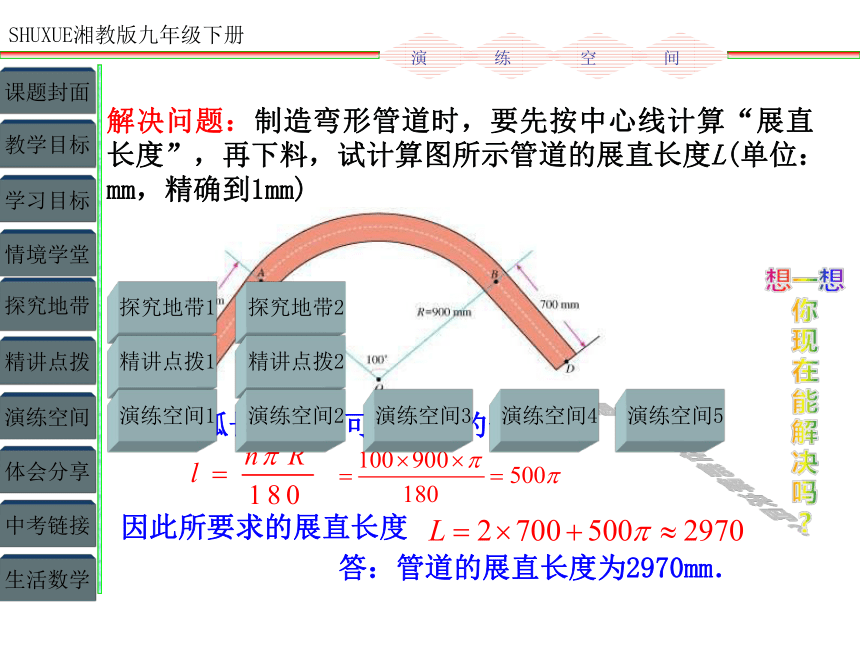
解决问题:制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
答:管道的展直长度为2970mm.
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
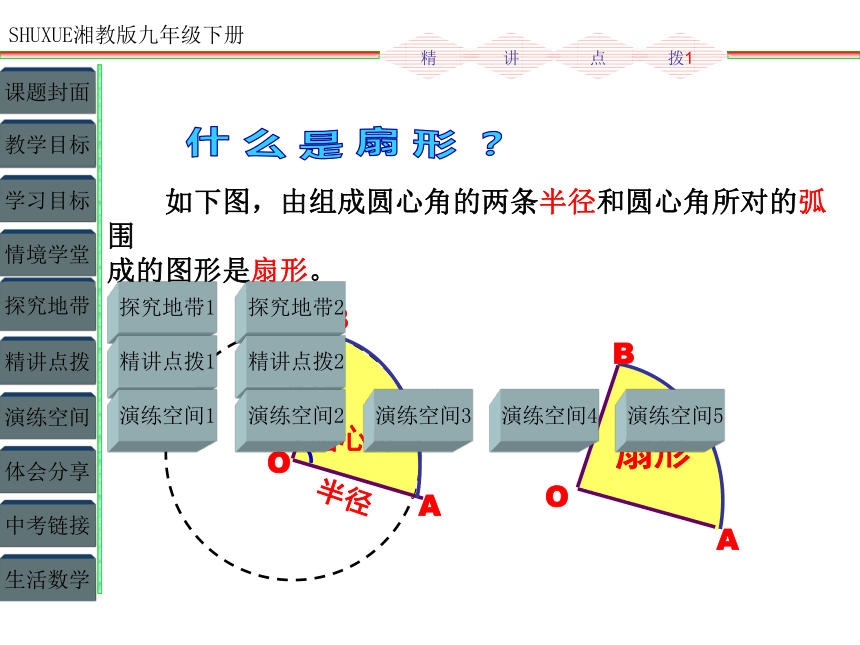
如下图,由组成圆心角的两条半径和圆心角所对的弧围
成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
精
讲
点
拨1
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
演
练
空
间2
下列各图中,哪些图形是扇形?为什么?
O
A
B
C
A
O
B
C
(1)
O
A
B
C
(2)
(3)
O
A
B
(4)
O
A
B
(5)
请在你认为是扇形的图形序号前打√:
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
(1)半径为R的圆,面积是__________
S=πR2
(3)圆心角为1°的扇形的面积是______
(4)圆心角为n°的扇形的面积是圆
心角为1°的扇形的面积的______倍,
是圆面积的__________
n
(5)圆心角为n°的扇形的面积是______
自学教材P88----P89,思考下列内容:
A
B
O
n°
(2)圆的面积可以看作是______度的圆心角所对的扇形
360
探
究
地
带2
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形,则
注意:
(1)公式中n的意义.n表示1°圆心角的倍数,它是
不带单位的;
(2)公式要理解记忆(即按照上面推导过程记忆).
探
究
地
带
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
3.圆心角是1800的扇形面积是多少?
圆心角是900的扇形面积是多少?
圆心角是2700的扇形面积是多少?
2.(当圆半径一定时)扇形的面积随着圆心角的增大
而______。
增大
个圆面积
个圆面积
1.扇形的弧长和面积都由_______、________决定?
演
练
空
间3
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少?
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
问题:扇形的弧长公式与面积公式有联系吗?
想一想:扇形的面积公式与什么公式类似?
精
讲
点
拨2
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知扇形的半径为3cm,扇形的弧长为
πcm,则该扇形的面积是______cm2,
演
练
空
间4
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
0
B
A
C
D
弓形的面积 = S扇- S⊿
提示:要求的面积,可以通过哪些图形面积的和或差求得
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:
∴OD=OC-DC=0.6-0.3=0.3
∴∠AOD=60°, ∠ AOB=120°
在Rt△ OAD中,∵OD=0.5OA
0.6
0.3
0
B
A
C
D
∴∠ OAD=30°
有水部分的面积为=
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
通过本节课的学习,
我知道了……
学到了……感受到了……
体
会
分
享
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
2. 扇形面积公式与弧长公式的区别:
S扇形= S圆
360
n
l弧= C圆
360
n
1.扇形的弧长和面积大小与哪些因素有关?
(2)与半径的长短有关
(1)与圆心角的大小有关
体
会
分
享
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
1.如图,已知扇形AOB的半径为10,∠AOB=60°,
求弧AB的长和扇形AOB的面积
(写详细过程)
2.如果一个扇形面积是它所在圆的面积的
,则此扇形的圆心角是_________
3、已知扇形的半径为3cm,扇形的弧长为πcm,
则该扇形的积是__cm2,扇形的圆心角为___°.
演
练
空
间5
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
1.扇形的面积是它所在圆的面积的 ,求这个扇形的圆心角的度数;(05陕西)
2.扇形的面积是S,它的半径是r,求这个扇形的弧长;(05年太原)
3.扇形所在圆的圆心角度数为150°,L=20πcm,
求:(1).扇形所在圆的半径;
(2).扇形的面积; (05年台州)
4.如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。 (07年山东)
中
考
链
接
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
1如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
生
活
数
学
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
A
D
B
C
.E
如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
生
活
数
学
课
堂
宣
言
你棒!他棒!我最棒!Ye ……….
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
课
题
封
面
教
学
目
标
认识扇形,会计算弧长和扇形的面积,
通过弧长和扇形面积的发现与推导,
培养学生运用已有知识探究问题获得新知的能力。
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
了解扇形的概念,
理解n°的圆心角所对的弧长和扇形面积的计算公式,
并应用这些公式解决相关问题。
学
习
目
标
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
情
境
学
堂
制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
(1)半径为R的圆,周长是_________
C=2πR
(3)圆心角是10的扇形是圆周长的_____
A
B
O
n°
(4)n°圆心角所对的弧长是
1°圆心角所对的弧长的______倍,
是圆周长的__________
n
(5)n°圆心角所对弧长是__________
自学教材P86----P87,思考下列内容:
(2)圆的周长可以看作是_____度的圆心角
所对的弧
360
1°圆心角所对弧长是__________
探
究
地
带1
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
若设⊙O半径为R,n°的圆心角所对
的弧长为l,则
l
A
B
O
n°
在应用弧长公式
进行计算时,要注意公式中n的意义,n表示1°圆心角的倍数,它是不带单位的;
注意:
探
究
地
带
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知弧所对的圆周角为90°,半径是4,
则弧长为多少?
演
练
空
间1
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
解决问题:制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
答:管道的展直长度为2970mm.
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
如下图,由组成圆心角的两条半径和圆心角所对的弧围
成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
精
讲
点
拨1
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
演
练
空
间2
下列各图中,哪些图形是扇形?为什么?
O
A
B
C
A
O
B
C
(1)
O
A
B
C
(2)
(3)
O
A
B
(4)
O
A
B
(5)
请在你认为是扇形的图形序号前打√:
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
(1)半径为R的圆,面积是__________
S=πR2
(3)圆心角为1°的扇形的面积是______
(4)圆心角为n°的扇形的面积是圆
心角为1°的扇形的面积的______倍,
是圆面积的__________
n
(5)圆心角为n°的扇形的面积是______
自学教材P88----P89,思考下列内容:
A
B
O
n°
(2)圆的面积可以看作是______度的圆心角所对的扇形
360
探
究
地
带2
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形,则
注意:
(1)公式中n的意义.n表示1°圆心角的倍数,它是
不带单位的;
(2)公式要理解记忆(即按照上面推导过程记忆).
探
究
地
带
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
3.圆心角是1800的扇形面积是多少?
圆心角是900的扇形面积是多少?
圆心角是2700的扇形面积是多少?
2.(当圆半径一定时)扇形的面积随着圆心角的增大
而______。
增大
个圆面积
个圆面积
1.扇形的弧长和面积都由_______、________决定?
演
练
空
间3
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少?
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
问题:扇形的弧长公式与面积公式有联系吗?
想一想:扇形的面积公式与什么公式类似?
精
讲
点
拨2
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
已知扇形的半径为3cm,扇形的弧长为
πcm,则该扇形的面积是______cm2,
演
练
空
间4
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。
0
B
A
C
D
弓形的面积 = S扇- S⊿
提示:要求的面积,可以通过哪些图形面积的和或差求得
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:
∴OD=OC-DC=0.6-0.3=0.3
∴∠AOD=60°, ∠ AOB=120°
在Rt△ OAD中,∵OD=0.5OA
0.6
0.3
0
B
A
C
D
∴∠ OAD=30°
有水部分的面积为=
演
练
空
间
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
通过本节课的学习,
我知道了……
学到了……感受到了……
体
会
分
享
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
2. 扇形面积公式与弧长公式的区别:
S扇形= S圆
360
n
l弧= C圆
360
n
1.扇形的弧长和面积大小与哪些因素有关?
(2)与半径的长短有关
(1)与圆心角的大小有关
体
会
分
享
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
1.如图,已知扇形AOB的半径为10,∠AOB=60°,
求弧AB的长和扇形AOB的面积
(写详细过程)
2.如果一个扇形面积是它所在圆的面积的
,则此扇形的圆心角是_________
3、已知扇形的半径为3cm,扇形的弧长为πcm,
则该扇形的积是__cm2,扇形的圆心角为___°.
演
练
空
间5
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
1.扇形的面积是它所在圆的面积的 ,求这个扇形的圆心角的度数;(05陕西)
2.扇形的面积是S,它的半径是r,求这个扇形的弧长;(05年太原)
3.扇形所在圆的圆心角度数为150°,L=20πcm,
求:(1).扇形所在圆的半径;
(2).扇形的面积; (05年台州)
4.如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。 (07年山东)
中
考
链
接
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
1如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
生
活
数
学
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
A
D
B
C
.E
如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
生
活
数
学
课
堂
宣
言
你棒!他棒!我最棒!Ye ……….
探究地带1
探究地带2
精讲点拨1
精讲点拨2
演练空间1
演练空间2
演练空间3
演练空间4
演练空间5
