山东省德州市2012届高三4月份第二次模拟考试数学(文)word版
文档属性
| 名称 | 山东省德州市2012届高三4月份第二次模拟考试数学(文)word版 |

|
|
| 格式 | zip | ||
| 文件大小 | 512.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-10 00:00:00 | ||
图片预览



文档简介
山东省德州市
2012届高三4月份第二次模拟考试
数学(文)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷60分,第Ⅱ卷90分,共150分,测试时间120分钟。
第I卷(共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知全集=
A.(-2,-1) B. C. D.
2.若复数是纯虚数,则实数a的值为
A.2 B. C.-2 D.
3.已知数列=
A.8 B.16 C.31 D.32
4.已知向量=
A.0 B.4 C.8 D.
5.右图为甲,乙两名学生7次考试成绩的茎叶图(其中m为数字0~9中
的一个),去掉一个最高分和一个最低分后,甲、乙考试成绩的平均数
分别为a和b,则一定有
A. B.
C. D.的大小与m的值有关
6.在长为16cm的线段AB上任取一点M,并以线段AM为一边作正方形,则此正方形的面积介于25cm2与81cm2之间的概率为
A. B. C. D.
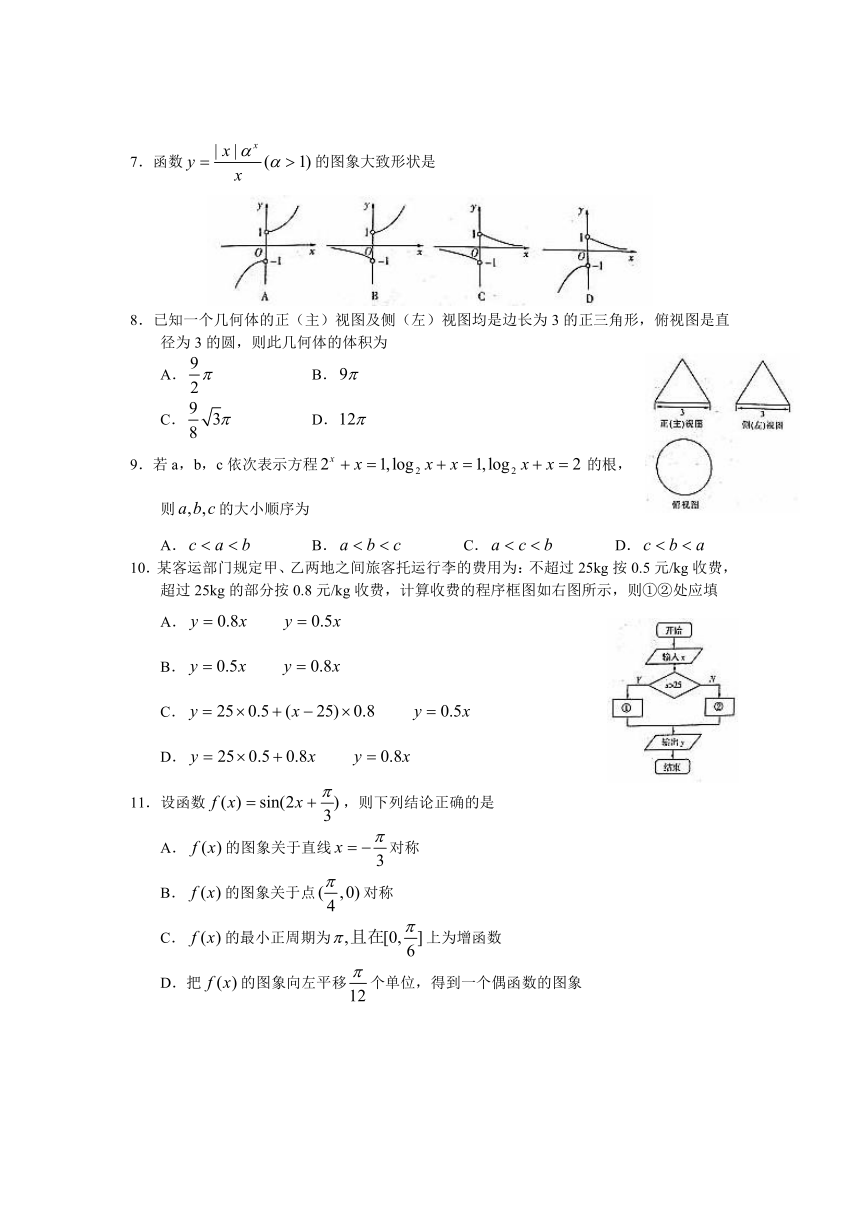
7.函数的图象大致形状是
8.已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为
A. B.
C. D.
9.若a,b,c依次表示方程的根,
则的大小顺序为
A. B. C. D.
10.某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填
A.
B.
C.
D.
11.设函数,则下列结论正确的是
A.的图象关于直线对称
B.的图象关于点对称
C.的最小正周期为上为增函数
D.把的图象向左平移个单位,得到一个偶函数的图象
12.设双曲线的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A、B两点,且与双曲线在第一象限的交点为P,设Q为坐标原点,若,且,则该双曲线的离心率为
A. B. C. D.
第II卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
13.设函数 。
14.设斜率为1的直线l过抛物线的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为8,则a的值为 。
15.若实数的最小值为—2,则实数m= 。
16.已知下列四下命题:
①命题“若”的否命题为“若”;
②命题“若”的逆命题为真命题;
③命题“”的否定是“”;
④“”是“”的充分不必要条件
其中正确命题的序号是 。
三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
在△ABC中,角A,B,C的对边分别是a、b、c,已知且m//n.
(I)求角A的大小;
(II)若的值。
18.(本小题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班60人进行了问卷调查得到了如下的2×2列联表:
(I)用分层抽样的方法在喜爱打篮球的学生中抽6人,其中男生抽多少人?
(II)在上述抽取的人中选2人,求恰有一名女生的概率;
(III)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由。
下面的临界值表供参考:
19.(本小题满分12分)
已知正项等差数列成等比数列。
(I)求数列的通项公式;
(II)设,试问当n为何值时,最大,并求出 的最大值。
20.(本小题满分12分)
如图,四棱锥P—ABCD的底面是平行四边形,PA⊥平面ABCD,AC⊥AB,点E是PD的中点。
(I)求证:PB⊥AC;
(II)求证:PB//平面ACE;
(III)求三棱锥E—ABC与四棱锥P—ABCD的体积之比。
21.(本小题满分12分)
已知椭圆C的中心为原点O,点F(1,0)是它的一个焦点,直线l过点F与椭圆C交于A,B两点,当直线l垂直于x轴时,
(I)求椭圆C的方程;
(II)已知点P为椭圆的上顶点,且存在实数成立,求t的值和直线l的方程。
22.(本小题满分14分)
已知函数
(I)求函数处的切线方程;
(II)若方程有唯一解,试求实数m的取值范围;
(III)是否存在实数a使函数上均为增函数,若存在求a的取值范围;若不存在说明理由。
2012届高三4月份第二次模拟考试
数学(文)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷60分,第Ⅱ卷90分,共150分,测试时间120分钟。
第I卷(共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知全集=
A.(-2,-1) B. C. D.
2.若复数是纯虚数,则实数a的值为
A.2 B. C.-2 D.
3.已知数列=
A.8 B.16 C.31 D.32
4.已知向量=
A.0 B.4 C.8 D.
5.右图为甲,乙两名学生7次考试成绩的茎叶图(其中m为数字0~9中
的一个),去掉一个最高分和一个最低分后,甲、乙考试成绩的平均数
分别为a和b,则一定有
A. B.
C. D.的大小与m的值有关
6.在长为16cm的线段AB上任取一点M,并以线段AM为一边作正方形,则此正方形的面积介于25cm2与81cm2之间的概率为
A. B. C. D.
7.函数的图象大致形状是
8.已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为
A. B.
C. D.
9.若a,b,c依次表示方程的根,
则的大小顺序为
A. B. C. D.
10.某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填
A.
B.
C.
D.
11.设函数,则下列结论正确的是
A.的图象关于直线对称
B.的图象关于点对称
C.的最小正周期为上为增函数
D.把的图象向左平移个单位,得到一个偶函数的图象
12.设双曲线的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A、B两点,且与双曲线在第一象限的交点为P,设Q为坐标原点,若,且,则该双曲线的离心率为
A. B. C. D.
第II卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
13.设函数 。
14.设斜率为1的直线l过抛物线的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为8,则a的值为 。
15.若实数的最小值为—2,则实数m= 。
16.已知下列四下命题:
①命题“若”的否命题为“若”;
②命题“若”的逆命题为真命题;
③命题“”的否定是“”;
④“”是“”的充分不必要条件
其中正确命题的序号是 。
三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
在△ABC中,角A,B,C的对边分别是a、b、c,已知且m//n.
(I)求角A的大小;
(II)若的值。
18.(本小题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班60人进行了问卷调查得到了如下的2×2列联表:
(I)用分层抽样的方法在喜爱打篮球的学生中抽6人,其中男生抽多少人?
(II)在上述抽取的人中选2人,求恰有一名女生的概率;
(III)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由。
下面的临界值表供参考:
19.(本小题满分12分)
已知正项等差数列成等比数列。
(I)求数列的通项公式;
(II)设,试问当n为何值时,最大,并求出 的最大值。
20.(本小题满分12分)
如图,四棱锥P—ABCD的底面是平行四边形,PA⊥平面ABCD,AC⊥AB,点E是PD的中点。
(I)求证:PB⊥AC;
(II)求证:PB//平面ACE;
(III)求三棱锥E—ABC与四棱锥P—ABCD的体积之比。
21.(本小题满分12分)
已知椭圆C的中心为原点O,点F(1,0)是它的一个焦点,直线l过点F与椭圆C交于A,B两点,当直线l垂直于x轴时,
(I)求椭圆C的方程;
(II)已知点P为椭圆的上顶点,且存在实数成立,求t的值和直线l的方程。
22.(本小题满分14分)
已知函数
(I)求函数处的切线方程;
(II)若方程有唯一解,试求实数m的取值范围;
(III)是否存在实数a使函数上均为增函数,若存在求a的取值范围;若不存在说明理由。
同课章节目录
