1.5 有理数的乘方(第1课时) 课件 2021-2022学年人教版数学 七年级上册(48张)
文档属性
| 名称 | 1.5 有理数的乘方(第1课时) 课件 2021-2022学年人教版数学 七年级上册(48张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 536.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 00:00:00 | ||
图片预览










文档简介
1.5 有理数的乘方
人教版· 数学· 七年级(上)
第一章 有理数
第1课时 乘方
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义。
2.能够正确进行有理数的乘方运算。
3.熟练地按有理数运算顺序进行混和运算。
学习目标
珠穆朗玛峰是世界的最高峰,它的海拔是8848.8米.把一张足够大的厚度为0.1毫米的纸,连续对折30次(假设能对折这么多次)的厚度能超过珠穆朗玛峰,这是真的吗?
导入新知
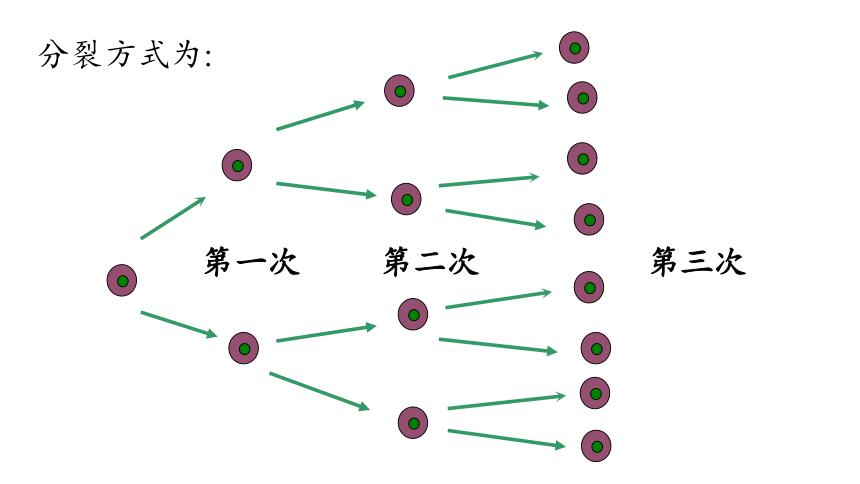
某种细胞每30分钟便由一个分裂成两个. 经过3小时这种细胞由1个能分裂成多少个?
新知一 有理数的乘方的意义
合作探究
第一次
第二次
第三次
分裂方式为:
这个细胞分裂一次可得多少个细胞?
那么,3小时共分裂了多少次?有多少个细胞?
解:一次:
2个;
2×2个;
2×2×2个;
六次: 2×2×2×2×2×2个.
分裂两次呢?
分裂三次呢?四次呢?
2×2×2×2个;
两次:
三次:
四次:
上面的式子有什么相同点?
它们都是乘法;并且它们各自的因数都相同.
同学们想一想:这样的运算能像平方、立方那样简写吗?
例如:2×2×2×2,
2×2×2×2×2×2,
记作24,
记作26,
一般地,n 个相同的因数a相乘,记作 an,读作“a 的 n 次幂(或 a 的 n 次方)”.
a·a·a· … · a = an
n个a
读作 2 的 6 次方(幂).
读作 2 的 4 次方(幂).
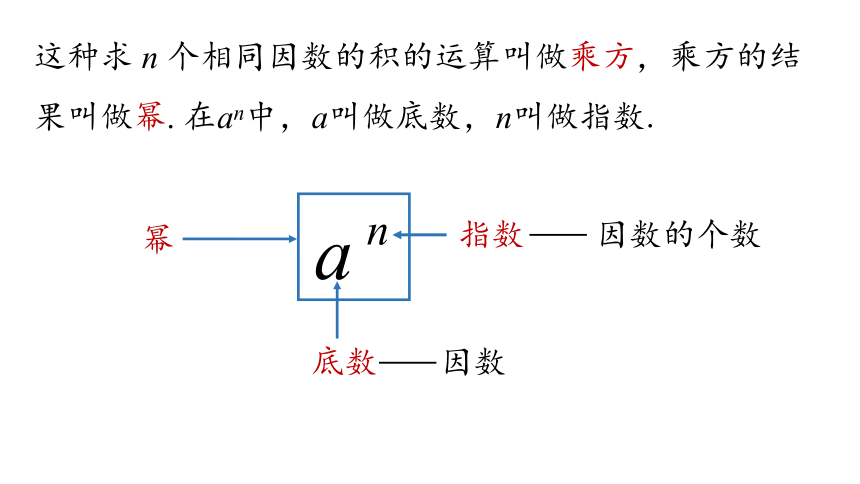
这种求 n 个相同因数的积的运算叫做乘方,乘方的结果叫做幂. 在an中,a叫做底数,n叫做指数.
幂
指数
因数的个数
底数
因数
注意:1.一个数可以看作这个数本身的一次方,
例如,5就是51,指数 1 通常省略不写.
2.指数是 2 时读作平方(或二次方),指数是 3 时读作立方(或三次方).例如,n2 读作“n 的平方”(或“n 的二次方”),n3 读作“n的立方”(或“n的三次方”).
3.指数 n 是正整数,底数 a 可以是任意有理数.
4.乘方是一种运算,幂是乘方的结果.
5.书写幂时,如果底数是负数或分数,
应将底数用括号括起来.
活学巧记
同因数相乘化乘方,
因数来把底数当;
因数个数是指数,
底为负(数)分(数)要括上.
例 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
你发现负数的幂的正负有什么规律?
1.负数的奇次幂是负数,负数的偶次幂是正数;
2.正数的任何次幂都是正数;
3.0的任何正整数次幂都是0.
有理数的乘方运算的符号法则:
注意:任何数的偶次幂都是非负数,1的任何次幂都是1,-1的偶次幂是1,-1的奇次幂是-1.
有理数的乘方运算:
计算一个有理数的乘方时,应将乘方运算转化为乘法运算,先确定幂的符号,再计算幂的绝对值.
例 用计算器计算(-8)5和(-3)6.
显示结果为-32 768.
=
)
(-)
(
<
3
6
显示结果为729.
所以(-8)5=-32 768,(-3)6=729.
=
)
(-)
(
<
8
5
解:
把下列各式写成乘方的形式,并指出底数、指数各是什么.
(1) (-2)× (-2)× (-2);
(2) 23×23×23×23;
(3) m·m·m·…·m.
?
2n 个m
(-2)3,底数是 -2,指数是 3.
(23)4,底数是 23?,指数是 4.
?
m2n,底数是 m,指数是 2n.
巩固新知
上式含有哪几种运算?先算什么,后算什么?
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
新知二 有理数的乘方运算
合作探究
有理数混合运算的顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
进行有理数的混合运算时,在遵守运算顺序的前提下,灵活运用运算律,可以使运算准确、快捷.
例 计算:
(1)2×(-3)3-4×(-3)+15;
(2)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2).
解:(1)原式=2×(-27)-(-12)+15
=-54+12+15
=-27.
=-8+(-3)×18-(-4.5)
(2)原式=-8+(-3)×(16+2)-9÷(-2)
=-8-54+4.5
=-57.5.
解:(1)原式=1×2+(-8)÷4
=2+(-2)
=0.
(2) 原式=-125 - 3×116
?
计算:
=-125 - 316
?
=-125316
?
巩固新知
1.计算 4+(-2)2×5=( )
A.-16 B.16 C.20 D.24
D
注意有理数混合运算的顺序
课堂练习
2.计算: -14???1???0.5×13×[3??(?32)].
?
解:-14??1?0.5×13×[3?(?32)]?
?
=-3 .
?
=-1?12×13×[3?(?9)]
?
=-1?12×13×12
?
=-1?2
?
1.求几个相同因数的积的运算,叫做乘方.
2.乘方运算的符号法则:
(1) 正数的任何次幂都是正数;
(2) 负数的奇次幂是负数,负数的偶次幂是正数;
(3) 0的任何正整数次幂都是0.
幂
指数
底数
归纳新知
3.有理数的混合运算顺序:
(1) 先乘方,再乘除,最后加减;
(2) 同级运算,从左到右进行;
(3) 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.(-2)3表示( )
A.2乘以-3 B.2个-3相加
C.3个-2相加 D.3个-2相乘
D
课后练习
3.-56表示的意义是_________________________,其中底数是____,指数是_____.
6个5相乘所得积的相反数
5
6
D
5.计算下列各式,其结果为负数的是( )
A.-(-3) B.|-3|
C.(-3)3 D.(-3)2
C
B
A
8.下列计算正确的是( )
A.32=6 B.(-2)3=8
C.|-2|=2 D.-22=4
9.计算(-18)+(-1)9的值是( )
A.0 B.2 C.-2 D.不能确定
10.若一个有理数的平方是正数,则这个有理数的立方是( )
A.正数 B.负数
C.正数或负数 D.整数
C
C
C
C
12.数轴上点A表示的数是(-3)2,将点A向左移动2个单位长度得到点B,则点B表示的数是____.
13.若x,y互为倒数,则(-xy)2 020=____.
7
1
14.计算:
(1)(-5)2; (2)-(-10)4;
解:25
解:-10 000
15.用计算器计算:
(1)(-7)5; (2)86; (3)6.23; (4)(-5.3)4.
解:(1)(-7)5=-16 807.
(2)86=262 144.
(3)6.23=238.328.
(4)(-5.3)4=789.048 1
16.式子-22+(-2)2-(-2)3-23的值为( )
A.-2 B.6
C.-18 D.0
D
D
18.若a2=4,b2=9,则a-b=_______________.
1或-1或5或-5
19.计算:
(1)-32×(-3)2;
解:-81
21.有一块面积为64平方米的正方形纸片,第1次剪掉一半,第2次剪掉剩下纸片的一半,如此继续剪下去,第6次后剩下的纸片的面积是多少平方米?
解:(2)当n=1,2时,nn+1<(n+1)n;当n≥3时,nn+1>(n+1)n.(3)99100>10099.
再
见
人教版· 数学· 七年级(上)
第一章 有理数
第1课时 乘方
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义。
2.能够正确进行有理数的乘方运算。
3.熟练地按有理数运算顺序进行混和运算。
学习目标
珠穆朗玛峰是世界的最高峰,它的海拔是8848.8米.把一张足够大的厚度为0.1毫米的纸,连续对折30次(假设能对折这么多次)的厚度能超过珠穆朗玛峰,这是真的吗?
导入新知
某种细胞每30分钟便由一个分裂成两个. 经过3小时这种细胞由1个能分裂成多少个?
新知一 有理数的乘方的意义
合作探究
第一次
第二次
第三次
分裂方式为:
这个细胞分裂一次可得多少个细胞?
那么,3小时共分裂了多少次?有多少个细胞?
解:一次:
2个;
2×2个;
2×2×2个;
六次: 2×2×2×2×2×2个.
分裂两次呢?
分裂三次呢?四次呢?
2×2×2×2个;
两次:
三次:
四次:
上面的式子有什么相同点?
它们都是乘法;并且它们各自的因数都相同.
同学们想一想:这样的运算能像平方、立方那样简写吗?
例如:2×2×2×2,
2×2×2×2×2×2,
记作24,
记作26,
一般地,n 个相同的因数a相乘,记作 an,读作“a 的 n 次幂(或 a 的 n 次方)”.
a·a·a· … · a = an
n个a
读作 2 的 6 次方(幂).
读作 2 的 4 次方(幂).
这种求 n 个相同因数的积的运算叫做乘方,乘方的结果叫做幂. 在an中,a叫做底数,n叫做指数.
幂
指数
因数的个数
底数
因数
注意:1.一个数可以看作这个数本身的一次方,
例如,5就是51,指数 1 通常省略不写.
2.指数是 2 时读作平方(或二次方),指数是 3 时读作立方(或三次方).例如,n2 读作“n 的平方”(或“n 的二次方”),n3 读作“n的立方”(或“n的三次方”).
3.指数 n 是正整数,底数 a 可以是任意有理数.
4.乘方是一种运算,幂是乘方的结果.
5.书写幂时,如果底数是负数或分数,
应将底数用括号括起来.
活学巧记
同因数相乘化乘方,
因数来把底数当;
因数个数是指数,
底为负(数)分(数)要括上.
例 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
你发现负数的幂的正负有什么规律?
1.负数的奇次幂是负数,负数的偶次幂是正数;
2.正数的任何次幂都是正数;
3.0的任何正整数次幂都是0.
有理数的乘方运算的符号法则:
注意:任何数的偶次幂都是非负数,1的任何次幂都是1,-1的偶次幂是1,-1的奇次幂是-1.
有理数的乘方运算:
计算一个有理数的乘方时,应将乘方运算转化为乘法运算,先确定幂的符号,再计算幂的绝对值.
例 用计算器计算(-8)5和(-3)6.
显示结果为-32 768.
=
)
(-)
(
<
3
6
显示结果为729.
所以(-8)5=-32 768,(-3)6=729.
=
)
(-)
(
<
8
5
解:
把下列各式写成乘方的形式,并指出底数、指数各是什么.
(1) (-2)× (-2)× (-2);
(2) 23×23×23×23;
(3) m·m·m·…·m.
?
2n 个m
(-2)3,底数是 -2,指数是 3.
(23)4,底数是 23?,指数是 4.
?
m2n,底数是 m,指数是 2n.
巩固新知
上式含有哪几种运算?先算什么,后算什么?
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
新知二 有理数的乘方运算
合作探究
有理数混合运算的顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
进行有理数的混合运算时,在遵守运算顺序的前提下,灵活运用运算律,可以使运算准确、快捷.
例 计算:
(1)2×(-3)3-4×(-3)+15;
(2)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2).
解:(1)原式=2×(-27)-(-12)+15
=-54+12+15
=-27.
=-8+(-3)×18-(-4.5)
(2)原式=-8+(-3)×(16+2)-9÷(-2)
=-8-54+4.5
=-57.5.
解:(1)原式=1×2+(-8)÷4
=2+(-2)
=0.
(2) 原式=-125 - 3×116
?
计算:
=-125 - 316
?
=-125316
?
巩固新知
1.计算 4+(-2)2×5=( )
A.-16 B.16 C.20 D.24
D
注意有理数混合运算的顺序
课堂练习
2.计算: -14???1???0.5×13×[3??(?32)].
?
解:-14??1?0.5×13×[3?(?32)]?
?
=-3 .
?
=-1?12×13×[3?(?9)]
?
=-1?12×13×12
?
=-1?2
?
1.求几个相同因数的积的运算,叫做乘方.
2.乘方运算的符号法则:
(1) 正数的任何次幂都是正数;
(2) 负数的奇次幂是负数,负数的偶次幂是正数;
(3) 0的任何正整数次幂都是0.
幂
指数
底数
归纳新知
3.有理数的混合运算顺序:
(1) 先乘方,再乘除,最后加减;
(2) 同级运算,从左到右进行;
(3) 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.(-2)3表示( )
A.2乘以-3 B.2个-3相加
C.3个-2相加 D.3个-2相乘
D
课后练习
3.-56表示的意义是_________________________,其中底数是____,指数是_____.
6个5相乘所得积的相反数
5
6
D
5.计算下列各式,其结果为负数的是( )
A.-(-3) B.|-3|
C.(-3)3 D.(-3)2
C
B
A
8.下列计算正确的是( )
A.32=6 B.(-2)3=8
C.|-2|=2 D.-22=4
9.计算(-18)+(-1)9的值是( )
A.0 B.2 C.-2 D.不能确定
10.若一个有理数的平方是正数,则这个有理数的立方是( )
A.正数 B.负数
C.正数或负数 D.整数
C
C
C
C
12.数轴上点A表示的数是(-3)2,将点A向左移动2个单位长度得到点B,则点B表示的数是____.
13.若x,y互为倒数,则(-xy)2 020=____.
7
1
14.计算:
(1)(-5)2; (2)-(-10)4;
解:25
解:-10 000
15.用计算器计算:
(1)(-7)5; (2)86; (3)6.23; (4)(-5.3)4.
解:(1)(-7)5=-16 807.
(2)86=262 144.
(3)6.23=238.328.
(4)(-5.3)4=789.048 1
16.式子-22+(-2)2-(-2)3-23的值为( )
A.-2 B.6
C.-18 D.0
D
D
18.若a2=4,b2=9,则a-b=_______________.
1或-1或5或-5
19.计算:
(1)-32×(-3)2;
解:-81
21.有一块面积为64平方米的正方形纸片,第1次剪掉一半,第2次剪掉剩下纸片的一半,如此继续剪下去,第6次后剩下的纸片的面积是多少平方米?
解:(2)当n=1,2时,nn+1<(n+1)n;当n≥3时,nn+1>(n+1)n.(3)99100>10099.
再
见
