4.2 直线、射线、线段(第2课时) 课件 2021-2022学年人教版数学 七年级上册(45张)
文档属性
| 名称 | 4.2 直线、射线、线段(第2课时) 课件 2021-2022学年人教版数学 七年级上册(45张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 784.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 00:00:00 | ||
图片预览






文档简介
4.2 直线、射线、线段
人教版· 数学· 七年级(上)
第四章 几何图形初步
第2课时 比较线段的长短
1.会用尺规画一条线段等于已知线段,会比较两条线段的长短。(重点)
2.理解线段等分点的意义。(难点)
3.能够运用线段的和、差、倍、分关系求线段的长度。(重难点)
4.体会文字语言、符号语言和图形语言的相互转化。
学习目标
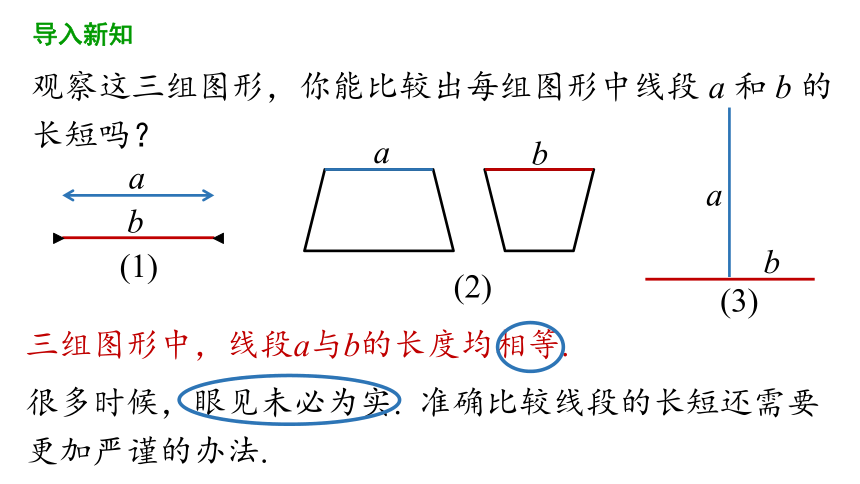
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
三组图形中,线段a与b的长度均相等.
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
(1)
a
b
(3)
a
b
(2)
a
b
导入新知
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以下办法.
新知一 线段的画法及长短比较
合作探究
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
在可打开角度的最大范围内,圆规可截取任意长度,相当于可以移动的“小木棍”.
作一条线段等于已知线段.
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
线段 AB 即为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
比较两个同学高矮的方法:
——叠合法
②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的数值进行比较.
——度量法
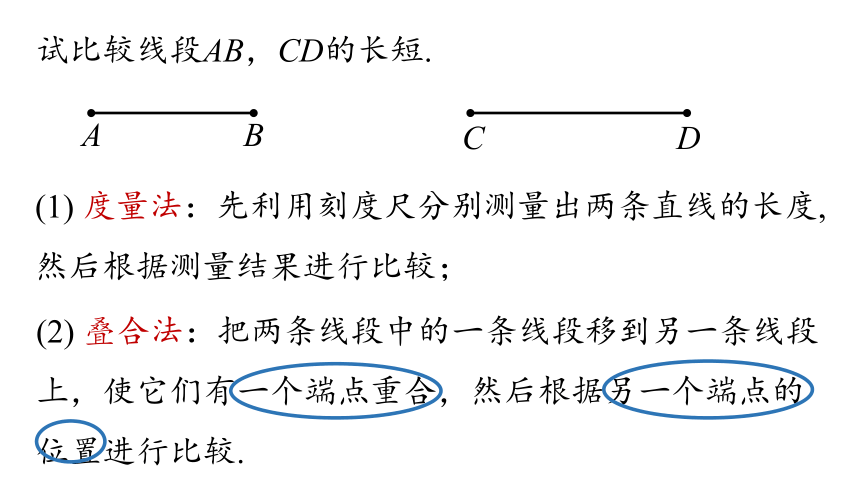
试比较线段AB,CD的长短.
(1) 度量法:先利用刻度尺分别测量出两条直线的长度,然后根据测量结果进行比较;
(2) 叠合法:把两条线段中的一条线段移到另一条线段上,使它们有一个端点重合,然后根据另一个端点的位置进行比较.
C D
A B
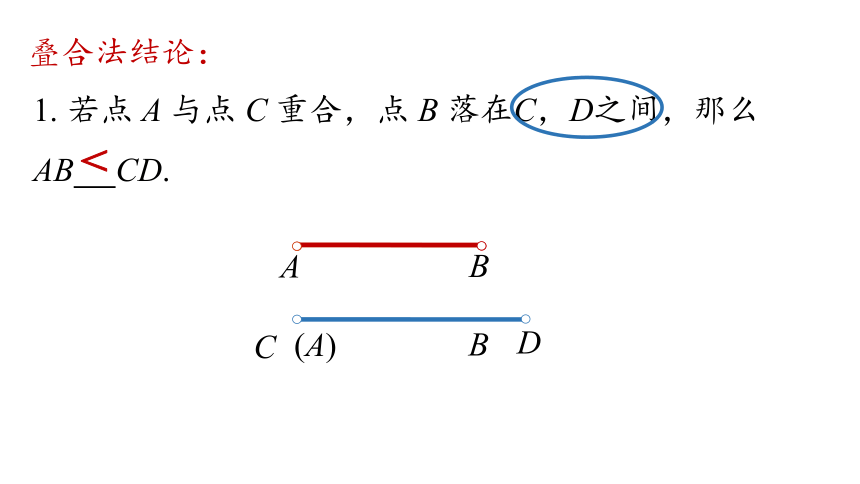
1. 若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB CD.
(A)
B
<
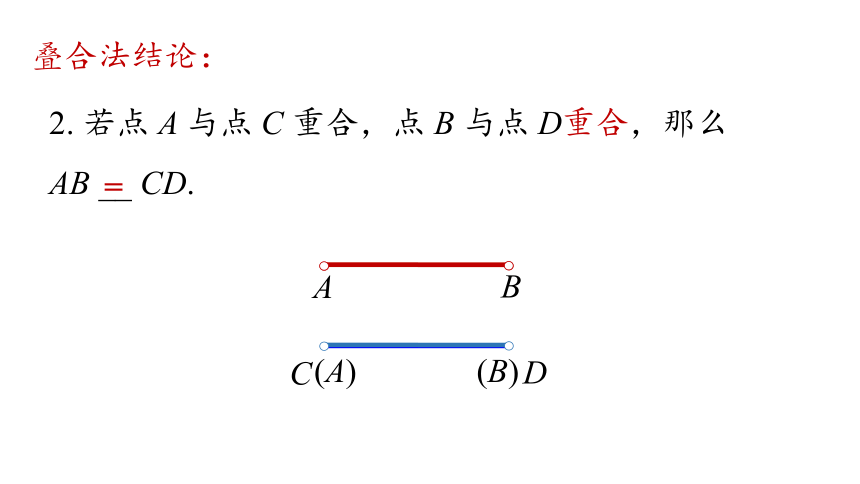
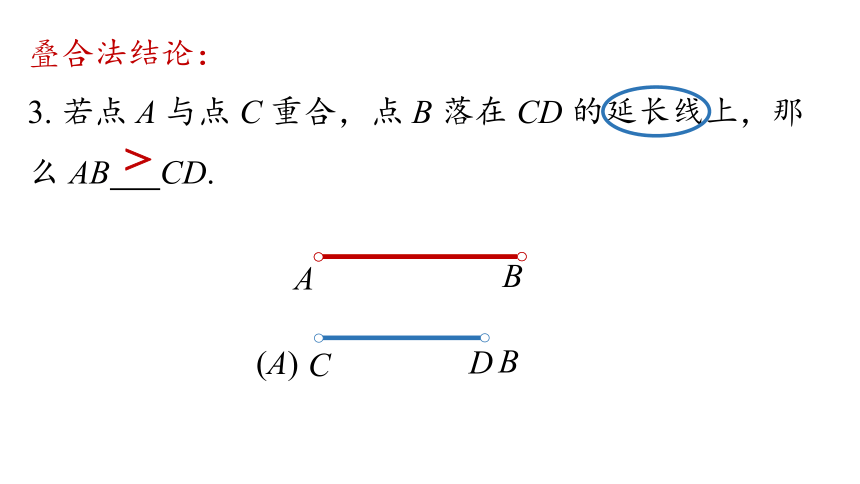
叠合法结论:
B
A
C
D
C
D
A
B
2. 若点 A 与点 C 重合,点 B 与点 D重合,那么
AB __ CD.
(A)
(B)
叠合法结论:
=
C
D
B
(A)
3. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB CD.
>
B
A
叠合法结论:
在直线上画出线段 AB=a?,再在 AB 的延长线上画线段 BC=b,线段 AC 就是 a 与 b 的和,记作 AC=a+b.
如果在 AB 上画线段 BD=b,那么线段 AD就是 a 与 b 的差,记作 AD= a-b.
A
B
C
D
a+b
a-b
a
b
b
线段的和差:
线段的倍、分:
如图所示,射线 AE 上有 B,C,D 三点,它们的长度关系是 AB=BC=CD,则 AC = 2BC,AD =3AB,AB=
12 AC,AB = 13 AD,AC= 23 AD.
?
A
B
C
D
例1 如图所示,若BC =CD,则 BD = CD,BC = BD,BC CE,AC CD(最后两空填“>”“<”或“=”).
解:因为BC=CD,
所以BD= BC+ CD= CD +CD=2CD,
BC= CD= CE - DE< CE,
2
12
?
<
>
所以BC= 12 BD,
?
AC=AB +BC=AB + CD > CD.
巩固新知
例2 为了比较线段AB与CD的大小,小明将点A与点
C重合使两条线段在一条直线上,结果点B在CD的
延长线上,则( )
A.AB<CD B.AB>CD
C.AB=CD D.以上都不对
B
例3 如图所示,AB=CD,则AC与BD的大小关系
是( )
A.AC>BD
B.AC<BD
C.AC=BD
D.无法确定
C
A
B
C
D
E
在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?
A
B
M
新知二 线段的中点
中点
合作探究
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = MB = 12 AB (或 AB = 2AM = 2MB).
?
反之也成立:因为AM=MB =12 AB (或 AB = 2 AM = 2 MB),
所以 M 是线段 AB 的中点.
?
类似地,还有线段的三等分点、四等分点等.
AM = MN = NB = 13 AB
?
(或 AB = 3AM = 3MN = 3NB)
N
M
B
A
线段的三等分点
AO = OP = PQ = QB = 14 AB
?
(或 AB=4AO =4OP =4PQ=4QB)
线段的四等分点
A
O
P
Q
B
注意:1. 线段的中点只有一个,且一定在线段上,类似地,线段的三等分点有两个、线段的四等分点有三个,且这些点都在线段上.
2. 若点 C 是线段AB的中点,则 AC= BC;但若 AC=BC,则点 C 不一定是线段 AB 的中点.
例如:如图,CA=CB,但点 C 不是线段 AB 的中点.
例4 下列说法正确的是( )
A. 若 AP= 12 AB,则点 P 为线段 AB 的中点
B. 若 AP=PB,则点 P 为线段 AB 的中点
C. 若 AB=2PB,则点 P 为线段 AB 的中点
D. 若 AP=PB= 12 AB,则点 P 为线段 AB 的中点
?
D
巩固新知
1.如图,点 D 是线段 AB 的中点,点 C 是线段 AD 的中点,若 CD=1,则AB= .
解:因为点 C 是线段 AD 的中点,
所以 AD=2CD =2.
因为点 D 是线段 AB 的中点,
所以 AB=2AD=4.
4
A
C
D
B
课堂练习
2.如图,M 是线段 AC 的中点,点 B 在线段 AC 上,且 AB=4,BC=2AB,求线段 MC 和线段 BM 的长.
A
B
M
C
解:因为AB=4, BC=2AB,
所以AC=AB+BC=4+8=12.
因为M是线段AC的中点,
所以MC=AM= AC=6,
所以BM=AM-AB=6-4=2.
12
?
所以BC=8,
3.如图,已知线段 a,b,c,用直尺和圆规作线段 AB,使 AB=a+3b -c.
A
B
C
解:(1) 作射线 AM;
(2) 在射线 AM 上截取 AC=a;
(3) 在射线 CM 上连续截取 CD=DE=EF=b;
(4) 在线段 FA 上截取 FB=c.则线段 AB 即为所求.
D
E
F
M
c
b
a
b
b
a
c
b
线段长短的比较与运算
线段长短的比较
线段的和、
差、倍、分
度量法
叠合法
中点
思想方法
方程思想
分类思想
基本作图
归纳新知
1.如图,已知线段a,b,c(a>b),作一条线段使它等于a+c-b,写出作法,保留作图痕迹.
解:作法:如图,①作射线AM;②在射线AM上顺次截取AB=a,BC=c;③在线段AC上截取CD=b.则线段AD=a+c-b即为所求.
课后练习
2.如图,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
C
3.比较线段AB与线段CD的大小,我们将点C与点A重合在一起,发现点D落在线段AB的延长线上,则AB_____CD.(填“>”“<”或“=”)
<
4.如图,下列关系式中与图形不符合的是( )
A.AD-CD=AC B.AC-BC=AB
C.AB+BD=AD D.AC+BD=AD
D
B
6.已知线段AB=10 cm,点C是AB的中点,点D是AC中点,
则线段CD=______cm.
2.5
7.如图, B,C为线段AD上的两点,C为线段AD的中点,AC=5厘米,BD=6厘米,求线段AB的长.
8.如图,点A,B在直线l上,点C是直线l外一点,可知CA+CB>AB,其依据是( )
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.直线比线段长
A
9.如图,从A地到B地的最短路线是( )
A.A→F→E→B
B.A→C→E→B
C.A→D→G→E→B
D.A→G→E→B
A
10.在一条直线上,依次有E,F,G,H四点.如果点F是线段EG的中点,点G是线段FH的中点,则有( )
A.EF=2GH B.EF>GH
C.EF>2GH D.EF=GH
D
11.如图,M,N两点把线段AB三等分,C为NB的中点,且CM=6 cm,则AB=______cm.
12
12.如图,有公共端点P的两条线段MP,NP组成一条折线M-P-N,若该折线M-P-N上一点Q把这条折线分成相等的两部分,我们把这个点Q叫做这条折线的“折中点”.已知点D是折线A-C-B的“折中点”,点E为线段AC的中点,CD=3,CE=5,则线段BC的长为_______.
4或16
13.如图,工厂A与工厂B想在公路m旁修建一座共用的仓库O,并且要求O到A与O到B的距离之和最短,请你在m上确定仓库应修建的O点位置,同时说明你选择该点的理由.
解:如图,连接AB交直线m于点O,
则O点即为所求的点.理由:因为两点的所有连线中,线段最短,所以OA+OB最短.
14.如图,B,C两点把线段AD分为2:4:3三部分,M是AD的中点,CD=6 cm,求线段MC的长.
15.如图,已知点C是线段AB的中点,点D在线段CB上,且BD=3,AD=15.
(1)求线段CD的长度;
(2)若将题中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
16.已知A,B,C三点在同一条直线上,若线段AB=20 cm,线段BC=8 cm,M,N分别是线段AB,BC的中点.
(1)求线段MN的长;
(2)根据(1)中的计算过程和结果,设AB=a,BC=b,且a>b,其他条件都不变,你能猜出MN的长度吗?(直接写出结果)
再
见
人教版· 数学· 七年级(上)
第四章 几何图形初步
第2课时 比较线段的长短
1.会用尺规画一条线段等于已知线段,会比较两条线段的长短。(重点)
2.理解线段等分点的意义。(难点)
3.能够运用线段的和、差、倍、分关系求线段的长度。(重难点)
4.体会文字语言、符号语言和图形语言的相互转化。
学习目标
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
三组图形中,线段a与b的长度均相等.
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
(1)
a
b
(3)
a
b
(2)
a
b
导入新知
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以下办法.
新知一 线段的画法及长短比较
合作探究
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
在可打开角度的最大范围内,圆规可截取任意长度,相当于可以移动的“小木棍”.
作一条线段等于已知线段.
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
线段 AB 即为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
比较两个同学高矮的方法:
——叠合法
②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的数值进行比较.
——度量法
试比较线段AB,CD的长短.
(1) 度量法:先利用刻度尺分别测量出两条直线的长度,然后根据测量结果进行比较;
(2) 叠合法:把两条线段中的一条线段移到另一条线段上,使它们有一个端点重合,然后根据另一个端点的位置进行比较.
C D
A B
1. 若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB CD.
(A)
B
<
叠合法结论:
B
A
C
D
C
D
A
B
2. 若点 A 与点 C 重合,点 B 与点 D重合,那么
AB __ CD.
(A)
(B)
叠合法结论:
=
C
D
B
(A)
3. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB CD.
>
B
A
叠合法结论:
在直线上画出线段 AB=a?,再在 AB 的延长线上画线段 BC=b,线段 AC 就是 a 与 b 的和,记作 AC=a+b.
如果在 AB 上画线段 BD=b,那么线段 AD就是 a 与 b 的差,记作 AD= a-b.
A
B
C
D
a+b
a-b
a
b
b
线段的和差:
线段的倍、分:
如图所示,射线 AE 上有 B,C,D 三点,它们的长度关系是 AB=BC=CD,则 AC = 2BC,AD =3AB,AB=
12 AC,AB = 13 AD,AC= 23 AD.
?
A
B
C
D
例1 如图所示,若BC =CD,则 BD = CD,BC = BD,BC CE,AC CD(最后两空填“>”“<”或“=”).
解:因为BC=CD,
所以BD= BC+ CD= CD +CD=2CD,
BC= CD= CE - DE< CE,
2
12
?
<
>
所以BC= 12 BD,
?
AC=AB +BC=AB + CD > CD.
巩固新知
例2 为了比较线段AB与CD的大小,小明将点A与点
C重合使两条线段在一条直线上,结果点B在CD的
延长线上,则( )
A.AB<CD B.AB>CD
C.AB=CD D.以上都不对
B
例3 如图所示,AB=CD,则AC与BD的大小关系
是( )
A.AC>BD
B.AC<BD
C.AC=BD
D.无法确定
C
A
B
C
D
E
在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?
A
B
M
新知二 线段的中点
中点
合作探究
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = MB = 12 AB (或 AB = 2AM = 2MB).
?
反之也成立:因为AM=MB =12 AB (或 AB = 2 AM = 2 MB),
所以 M 是线段 AB 的中点.
?
类似地,还有线段的三等分点、四等分点等.
AM = MN = NB = 13 AB
?
(或 AB = 3AM = 3MN = 3NB)
N
M
B
A
线段的三等分点
AO = OP = PQ = QB = 14 AB
?
(或 AB=4AO =4OP =4PQ=4QB)
线段的四等分点
A
O
P
Q
B
注意:1. 线段的中点只有一个,且一定在线段上,类似地,线段的三等分点有两个、线段的四等分点有三个,且这些点都在线段上.
2. 若点 C 是线段AB的中点,则 AC= BC;但若 AC=BC,则点 C 不一定是线段 AB 的中点.
例如:如图,CA=CB,但点 C 不是线段 AB 的中点.
例4 下列说法正确的是( )
A. 若 AP= 12 AB,则点 P 为线段 AB 的中点
B. 若 AP=PB,则点 P 为线段 AB 的中点
C. 若 AB=2PB,则点 P 为线段 AB 的中点
D. 若 AP=PB= 12 AB,则点 P 为线段 AB 的中点
?
D
巩固新知
1.如图,点 D 是线段 AB 的中点,点 C 是线段 AD 的中点,若 CD=1,则AB= .
解:因为点 C 是线段 AD 的中点,
所以 AD=2CD =2.
因为点 D 是线段 AB 的中点,
所以 AB=2AD=4.
4
A
C
D
B
课堂练习
2.如图,M 是线段 AC 的中点,点 B 在线段 AC 上,且 AB=4,BC=2AB,求线段 MC 和线段 BM 的长.
A
B
M
C
解:因为AB=4, BC=2AB,
所以AC=AB+BC=4+8=12.
因为M是线段AC的中点,
所以MC=AM= AC=6,
所以BM=AM-AB=6-4=2.
12
?
所以BC=8,
3.如图,已知线段 a,b,c,用直尺和圆规作线段 AB,使 AB=a+3b -c.
A
B
C
解:(1) 作射线 AM;
(2) 在射线 AM 上截取 AC=a;
(3) 在射线 CM 上连续截取 CD=DE=EF=b;
(4) 在线段 FA 上截取 FB=c.则线段 AB 即为所求.
D
E
F
M
c
b
a
b
b
a
c
b
线段长短的比较与运算
线段长短的比较
线段的和、
差、倍、分
度量法
叠合法
中点
思想方法
方程思想
分类思想
基本作图
归纳新知
1.如图,已知线段a,b,c(a>b),作一条线段使它等于a+c-b,写出作法,保留作图痕迹.
解:作法:如图,①作射线AM;②在射线AM上顺次截取AB=a,BC=c;③在线段AC上截取CD=b.则线段AD=a+c-b即为所求.
课后练习
2.如图,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
C
3.比较线段AB与线段CD的大小,我们将点C与点A重合在一起,发现点D落在线段AB的延长线上,则AB_____CD.(填“>”“<”或“=”)
<
4.如图,下列关系式中与图形不符合的是( )
A.AD-CD=AC B.AC-BC=AB
C.AB+BD=AD D.AC+BD=AD
D
B
6.已知线段AB=10 cm,点C是AB的中点,点D是AC中点,
则线段CD=______cm.
2.5
7.如图, B,C为线段AD上的两点,C为线段AD的中点,AC=5厘米,BD=6厘米,求线段AB的长.
8.如图,点A,B在直线l上,点C是直线l外一点,可知CA+CB>AB,其依据是( )
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.直线比线段长
A
9.如图,从A地到B地的最短路线是( )
A.A→F→E→B
B.A→C→E→B
C.A→D→G→E→B
D.A→G→E→B
A
10.在一条直线上,依次有E,F,G,H四点.如果点F是线段EG的中点,点G是线段FH的中点,则有( )
A.EF=2GH B.EF>GH
C.EF>2GH D.EF=GH
D
11.如图,M,N两点把线段AB三等分,C为NB的中点,且CM=6 cm,则AB=______cm.
12
12.如图,有公共端点P的两条线段MP,NP组成一条折线M-P-N,若该折线M-P-N上一点Q把这条折线分成相等的两部分,我们把这个点Q叫做这条折线的“折中点”.已知点D是折线A-C-B的“折中点”,点E为线段AC的中点,CD=3,CE=5,则线段BC的长为_______.
4或16
13.如图,工厂A与工厂B想在公路m旁修建一座共用的仓库O,并且要求O到A与O到B的距离之和最短,请你在m上确定仓库应修建的O点位置,同时说明你选择该点的理由.
解:如图,连接AB交直线m于点O,
则O点即为所求的点.理由:因为两点的所有连线中,线段最短,所以OA+OB最短.
14.如图,B,C两点把线段AD分为2:4:3三部分,M是AD的中点,CD=6 cm,求线段MC的长.
15.如图,已知点C是线段AB的中点,点D在线段CB上,且BD=3,AD=15.
(1)求线段CD的长度;
(2)若将题中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
16.已知A,B,C三点在同一条直线上,若线段AB=20 cm,线段BC=8 cm,M,N分别是线段AB,BC的中点.
(1)求线段MN的长;
(2)根据(1)中的计算过程和结果,设AB=a,BC=b,且a>b,其他条件都不变,你能猜出MN的长度吗?(直接写出结果)
再
见
