2021-2022学年人教版数学八年级上册11.1.1三角形的边暑期训练(word版有答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.1.1三角形的边暑期训练(word版有答案) | 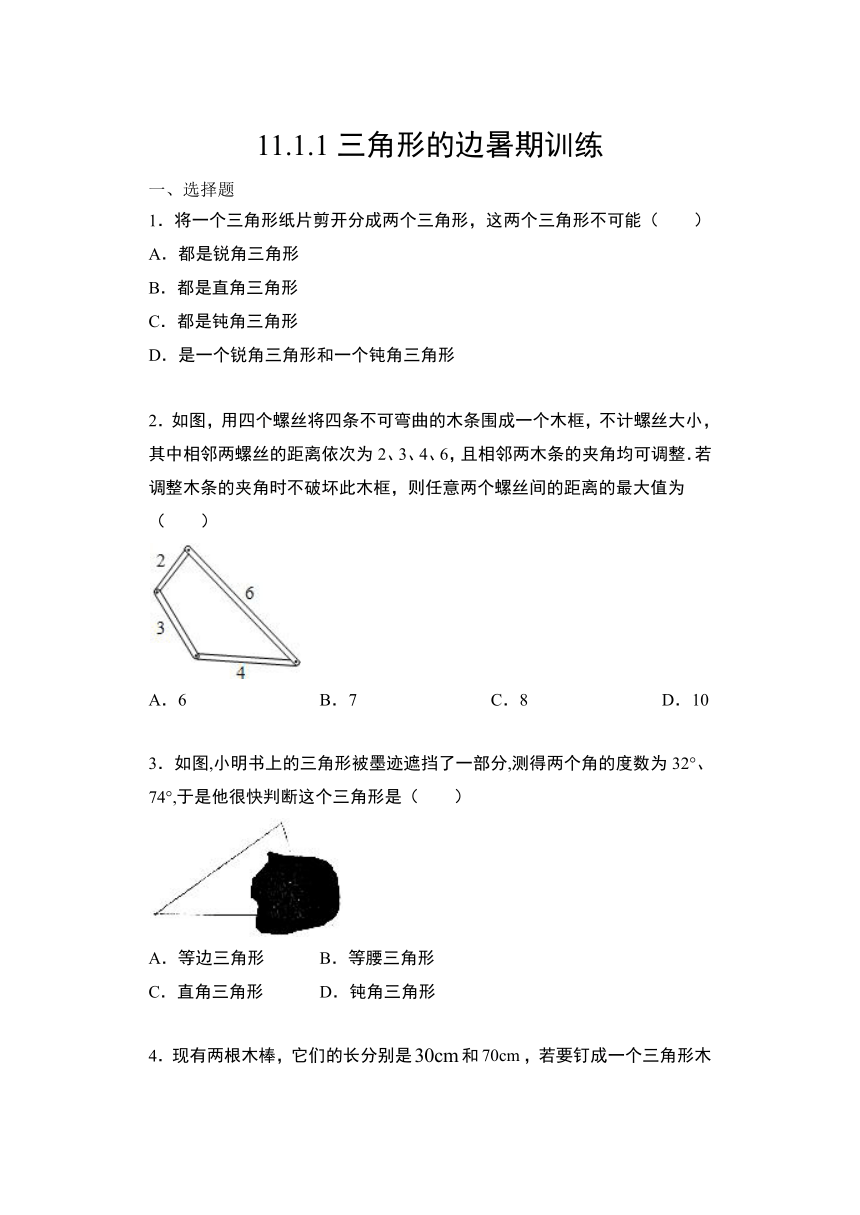 | |
| 格式 | docx | ||
| 文件大小 | 92.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 15:06:27 | ||
图片预览



文档简介
11.1.1三角形的边暑期训练
一、选择题
1.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能(
)
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
2.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为(
)
A.6
B.7
C.8
D.10
3.如图,小明书上的三角形被墨迹遮挡了一部分,测得两个角的度数为32°、74°,于是他很快判断这个三角形是(
)
A.等边三角形
B.等腰三角形
C.直角三角形
D.钝角三角形
4.现有两根木棒,它们的长分别是和,若要钉成一个三角形木架,则应选取的第三根木棒长可以为(
)
A.
B.
C.
D.
5.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上.则图中等腰三角形有
( )
A.1个
B.2个
C.3个
D.4个
6.若线段4、4、m能构成三角形,且m是整数,则m的最大值为(
)
A.10
B.8
C.7
D.4
7.a、b、c是三角形的三边长,化简后等于( )
A.
B.
C.
D.
8.已知三角形的两边长分别为1和4,则第三边长可能是(
)
A.3
B.4
C.5
D.6
9.三角形的两边长分别是4和11,第三边长为,则的取值范围在数轴上表示正确的是(
)
A.
B.
C.
D.
10.如果三角形的两边长分别为5和7,第三边长为偶数,那么这个三角形的周长可以是(
)
A.10
B.11
C.16
D.26
二、填空题
11.△ABC中,三边之比为3:4:5,且最长边为10m,则△ABC周长为_____cm.
12.若是△ABC的三边长,则化简的结果是________.
13.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对.
14.如果三角形的三边长分别为5,8,a,那么a的取值范围为__.
15.已知三角形三边长分别为m,n,k,且m、n满足,则这个三角形最长边k的取值范围是________.
16.三角形的3边长分别是xcm、cm、cm,它的周长不超过33cm.则x的取值范围是________.
三、解答题
17.已知,a,b,c为的三边,化简|a﹣b﹣c|﹣2|b﹣c﹣a|+|a+b﹣c|.
18.已知满足.
(1)求的值.
(2)以为边能否构成三角形,如果能,求出三角形的周长;如果不能,请说明理由.
19.小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.
(1)请用a表示第三条边长.
(2)问第一条边长可以为7m吗?请说明理由.
20.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
21.如图,点P为△ABC内任意一点,连接PB,PC,请说明不等式PB
+
PC<AB
+
AC的理由.
22.如图,已知P是△ABC内部的一点.
(1)度量AB,AC,PB,PC的长,根据度量结果比较AB+AC与PB+PC的大小.
(2)改变点P的位置,上述结论还成立吗?请说明理由.
答案
一、选择题
1.
A
2.
B
3.
B
4.
B
5.
C
6.
C
7.
B
8.
B
9.
A
10.
C
二、填空题
11.
2400
12.
2a
13.
3
14.
315.
16.
三、解答题
17.
﹣2a+4b﹣2c
18.
解:(1)根据题意得:a-2=0,b-3=0,c-4=0,
解得:a=2,b=3,c=4;
(2)∵2+3>4,
即a+b>c,
∴能构成三角形,
∴C△ABC=2+3+4=9.
19.
解:(1)第三边为:30﹣a﹣(2a+2)=(28﹣3a)m.
(2)第一条边长不可以为7m.
理由:a=7时,三边分别为7,16,7,
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7m.
20.
①△ABC是等腰三角形;周长为7;②△ABC的周长的最大值13,最小值11.
21.
解:延长BP交AC于点D
根据三角形的三边关系可得AB+AD>BD,PD+DC>PC
∴AB+AD+PD+DC>BD+PC
即AB+AC+PD>BP+PD+PC
∴AB+AC>BP+PC.
即PB+PC
AB+AC.
22.
(1)AB+AC>PB+PC(2)成立
试卷第8页,总8页
一、选择题
1.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能(
)
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
2.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为(
)
A.6
B.7
C.8
D.10
3.如图,小明书上的三角形被墨迹遮挡了一部分,测得两个角的度数为32°、74°,于是他很快判断这个三角形是(
)
A.等边三角形
B.等腰三角形
C.直角三角形
D.钝角三角形
4.现有两根木棒,它们的长分别是和,若要钉成一个三角形木架,则应选取的第三根木棒长可以为(
)
A.
B.
C.
D.
5.把两个都有一个锐角为30°的一样大小的直角三角形拼成如图所示的图形,两条直角边在同一直线上.则图中等腰三角形有
( )
A.1个
B.2个
C.3个
D.4个
6.若线段4、4、m能构成三角形,且m是整数,则m的最大值为(
)
A.10
B.8
C.7
D.4
7.a、b、c是三角形的三边长,化简后等于( )
A.
B.
C.
D.
8.已知三角形的两边长分别为1和4,则第三边长可能是(
)
A.3
B.4
C.5
D.6
9.三角形的两边长分别是4和11,第三边长为,则的取值范围在数轴上表示正确的是(
)
A.
B.
C.
D.
10.如果三角形的两边长分别为5和7,第三边长为偶数,那么这个三角形的周长可以是(
)
A.10
B.11
C.16
D.26
二、填空题
11.△ABC中,三边之比为3:4:5,且最长边为10m,则△ABC周长为_____cm.
12.若是△ABC的三边长,则化简的结果是________.
13.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对.
14.如果三角形的三边长分别为5,8,a,那么a的取值范围为__.
15.已知三角形三边长分别为m,n,k,且m、n满足,则这个三角形最长边k的取值范围是________.
16.三角形的3边长分别是xcm、cm、cm,它的周长不超过33cm.则x的取值范围是________.
三、解答题
17.已知,a,b,c为的三边,化简|a﹣b﹣c|﹣2|b﹣c﹣a|+|a+b﹣c|.
18.已知满足.
(1)求的值.
(2)以为边能否构成三角形,如果能,求出三角形的周长;如果不能,请说明理由.
19.小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.
(1)请用a表示第三条边长.
(2)问第一条边长可以为7m吗?请说明理由.
20.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
21.如图,点P为△ABC内任意一点,连接PB,PC,请说明不等式PB
+
PC<AB
+
AC的理由.
22.如图,已知P是△ABC内部的一点.
(1)度量AB,AC,PB,PC的长,根据度量结果比较AB+AC与PB+PC的大小.
(2)改变点P的位置,上述结论还成立吗?请说明理由.
答案
一、选择题
1.
A
2.
B
3.
B
4.
B
5.
C
6.
C
7.
B
8.
B
9.
A
10.
C
二、填空题
11.
2400
12.
2a
13.
3
14.
3
16.
三、解答题
17.
﹣2a+4b﹣2c
18.
解:(1)根据题意得:a-2=0,b-3=0,c-4=0,
解得:a=2,b=3,c=4;
(2)∵2+3>4,
即a+b>c,
∴能构成三角形,
∴C△ABC=2+3+4=9.
19.
解:(1)第三边为:30﹣a﹣(2a+2)=(28﹣3a)m.
(2)第一条边长不可以为7m.
理由:a=7时,三边分别为7,16,7,
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7m.
20.
①△ABC是等腰三角形;周长为7;②△ABC的周长的最大值13,最小值11.
21.
解:延长BP交AC于点D
根据三角形的三边关系可得AB+AD>BD,PD+DC>PC
∴AB+AD+PD+DC>BD+PC
即AB+AC+PD>BP+PD+PC
∴AB+AC>BP+PC.
即PB+PC
AB+AC.
22.
(1)AB+AC>PB+PC(2)成立
试卷第8页,总8页
