2021——2022学年七年级数学北师大版上册 第三章整式及其加减 3.2代数式 同步练习(word版含解析)
文档属性
| 名称 | 2021——2022学年七年级数学北师大版上册 第三章整式及其加减 3.2代数式 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 00:00:00 | ||
图片预览



文档简介
3.2代数式同步练习
一.代数式(共7小题)
1.下列代数式符合书写要求的是( )
A.7xy
B.ab×9
C.
D.1÷a
2.代数式x﹣y2的意义为( )
A.x的平方与y的平方的差
B.x与y的相反数的平方差
C.x与y的差的平方
D.x减去y的平方的差
3.下列代数式符合规范书写要求的是( )
A.﹣1x
B.1xy
C.0.3÷x
D.﹣a
4.下列式子,代数式有( )
A.6个
B.5个
C.4个
D.3个
5.下列说法中,正确的是( )
A.表示x,y,3,的积的代数式为3xy
B.a是代数式,1不是代数式
C.的意义是a与3的差除b的商
D.m,n两数的差的平方与m,n两数积的2倍的和表示为(m﹣n)2+2mn
6.已知一个等边三角形的边长为a,则3a所表示的实际意义是
.
7.在下列各式:①π﹣3;②ab=ba;③x;④2m﹣1>0:⑤;⑥8(x2+y2)中,代数式的有
个.
二.列代数式(共12小题)
8.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是( )
A.x+y
B.10xy
C.10(x+y)
D.10x+y
9.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
10.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园增加的面积为( )
A.a(b+x)
B.b(a+x)
C.ax
D.bx
11.某产品的成本为A元,按成本加价四成作为定价销售,因季节原因按定价的六折出售,降价后的售价为( )元.
A.(60%﹣40%)A
B.60%×40%A
C.(1+40%)60%A
D.(1+40%)(1﹣60%)A
12.甲数是乙数的4倍少3,则下列说法正确的是( )
①设乙数为x,甲数为4x﹣3
②设甲数为x,乙数为x+3
③设甲数为x,乙数为(x+3)
④设甲数为x,乙数为(x﹣3)
A.①③
B.①②
C.②④
D.①④
13.一个三位数,百位上的数字为x,十位上的数字比百位上的数字少3,个位上的数字是百位上的数字的2倍,这个三位数用含有x的代数式表示为( )
A.112x﹣30
B.100x﹣30
C.112x+30
D.102x+30
14.如果三角形底边上的高是6,底边长为x,那么三角形的面积y可以表示为
.
15.现有5元面值人民币m张,10元面值人民币n张,共有人民币
元(用含m、n的代数式表示).
16.如图是一块长方形场地ABCD,长AB=am,宽AD=bm,从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为
m2.(用含a,b的代数式表示)
17.一条河的水流速度是3km/h,船在静水中的速度是vkm/h,则该船在这条河流中顺水行驶的速度为
km/h.
18.如图是一个娱乐场,其中半圆形休息区和长方形游泳池以外的地方都是绿地,已知娱乐场的长为3a,宽为2a,游泳池的长、宽分别是娱乐场长、宽的一半,且半圆形休息区的直径是娱乐场宽的一半,则绿地的面积为
.(用含a的代数式表示,将结果化为最简)
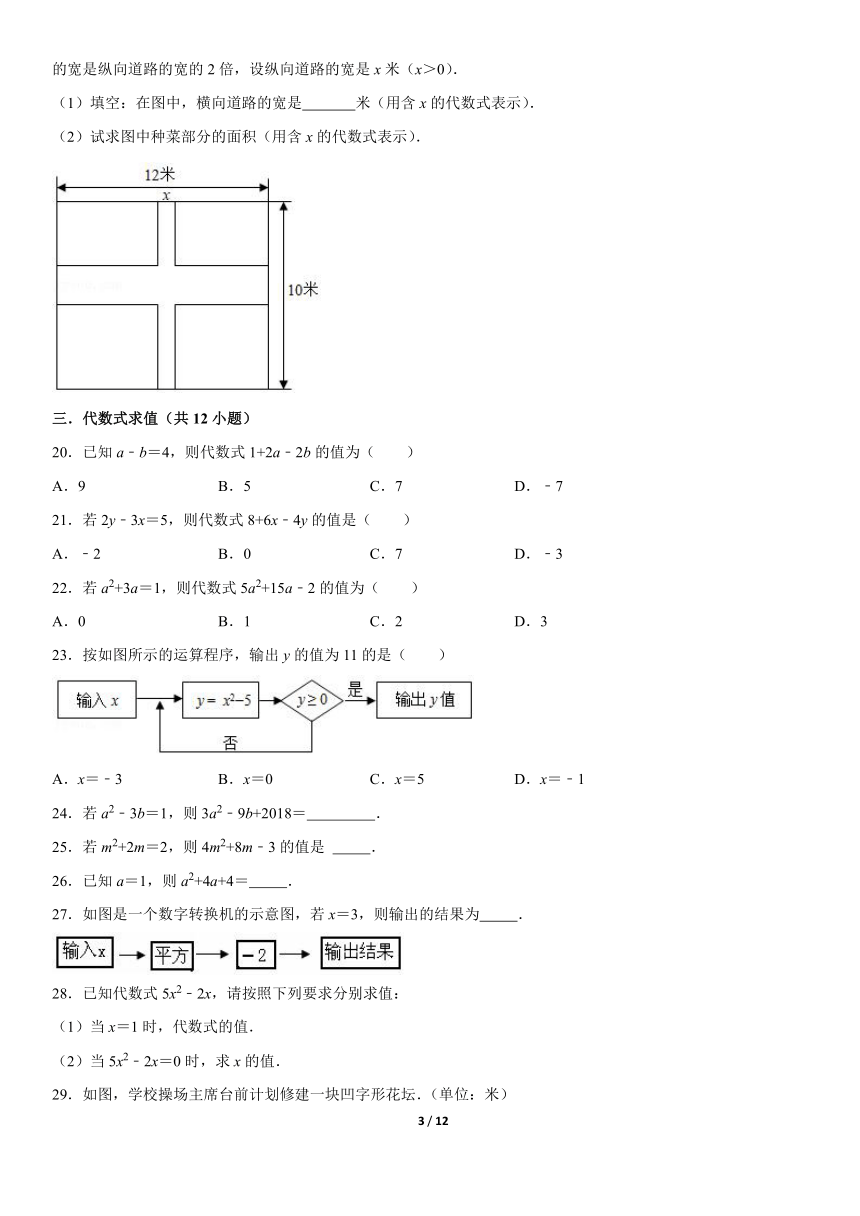
19.现有一块长方形菜地,长12米、宽10米.菜地中间欲铺设纵横两条路(图中空白部分)如图所示,横向道路的宽是纵向道路的宽的2倍,设纵向道路的宽是x米(x>0).
(1)填空:在图中,横向道路的宽是
米(用含x的代数式表示).
(2)试求图中种菜部分的面积(用含x的代数式表示).
三.代数式求值(共12小题)
20.已知a﹣b=4,则代数式1+2a﹣2b的值为( )
A.9
B.5
C.7
D.﹣7
21.若2y﹣3x=5,则代数式8+6x﹣4y的值是( )
A.﹣2
B.0
C.7
D.﹣3
22.若a2+3a=1,则代数式5a2+15a﹣2的值为( )
A.0
B.1
C.2
D.3
23.按如图所示的运算程序,输出y的值为11的是( )
A.x=﹣3
B.x=0
C.x=5
D.x=﹣1
24.若a2﹣3b=1,则3a2﹣9b+2018=
.
25.若m2+2m=2,则4m2+8m﹣3的值是
.
26.已知a=1,则a2+4a+4=
.
27.如图是一个数字转换机的示意图,若x=3,则输出的结果为
.
28.已知代数式5x2﹣2x,请按照下列要求分别求值:
(1)当x=1时,代数式的值.
(2)当5x2﹣2x=0时,求x的值.
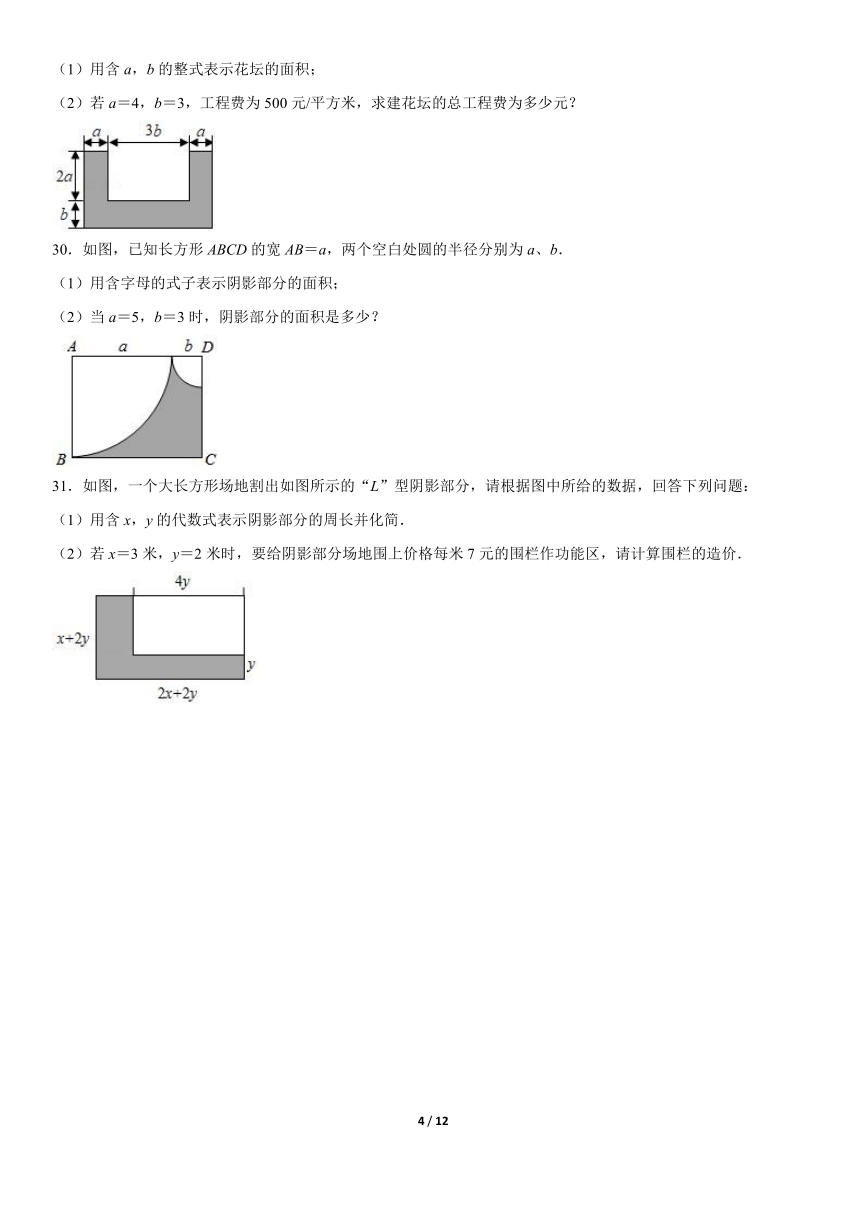
29.如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米)
(1)用含a,b的整式表示花坛的面积;
(2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元?
30.如图,已知长方形ABCD的宽AB=a,两个空白处圆的半径分别为a、b.
(1)用含字母的式子表示阴影部分的面积;
(2)当a=5,b=3时,阴影部分的面积是多少?
31.如图,一个大长方形场地割出如图所示的“L”型阴影部分,请根据图中所给的数据,回答下列问题:
(1)用含x,y的代数式表示阴影部分的周长并化简.
(2)若x=3米,y=2米时,要给阴影部分场地围上价格每米7元的围栏作功能区,请计算围栏的造价.
3.2代数式同步练习
参考答案与试题解析
一.代数式(共7小题)
1.下列代数式符合书写要求的是( )
A.7xy
B.ab×9
C.
D.1÷a
【解答】解:A、系数应为假分数,原书写错误,故此选项不符合题意;
B、系数应写在字母的前面,原书写错误,故此选项不符合题意;
C、符合要求,故此选项符合题意;
D、应写成分式的形式,原书写错误,故此选项不符合题意;
故选:C.
2.代数式x﹣y2的意义为( )
A.x的平方与y的平方的差
B.x与y的相反数的平方差
C.x与y的差的平方
D.x减去y的平方的差
【解答】解:在含有幂的运算中,先算y的平方,再计算x和y2的差.
故选:D.
3.下列代数式符合规范书写要求的是( )
A.﹣1x
B.1xy
C.0.3÷x
D.﹣a
【解答】解:A、原书写错误,应该写成﹣x,故此选项不符合题意;
B、原书写错误,应写成xy,故此选项不符合题意;
C、原书写错误,应写成,故此选项不符合题意;
D、原书写正确,故此选项符合题意.
故选:D.
4.下列式子,代数式有( )
A.6个
B.5个
C.4个
D.3个
【解答】解:代数式有:+b,0,d,8+y,共有4个.
故选:C.
5.下列说法中,正确的是( )
A.表示x,y,3,的积的代数式为3xy
B.a是代数式,1不是代数式
C.的意义是a与3的差除b的商
D.m,n两数的差的平方与m,n两数积的2倍的和表示为(m﹣n)2+2mn
【解答】解:A、表示x,y,3,的积的代数式为xy,原说法错误,故此选项不符合题意;
B、a是代数式,1也是代数式,原说法错误,故此选项不符合题意;
C、的意义是:a与3的差除以b的商,原说法错误,故此选项不符合题意;
D、m,n两数的差的平方与m,n两数积的2倍的和表示为(m﹣n)2+2mn,原说法正确,故此选项符合题意.
故选:D.
6.已知一个等边三角形的边长为a,则3a所表示的实际意义是 这个等边三角形的周长 .
【解答】解:因为等边三角形的边长为a,
所以3a所表示的实际意义是这个三角形的周长.
故答案为这个等边三角形的周长.
7.在下列各式:①π﹣3;②ab=ba;③x;④2m﹣1>0:⑤;⑥8(x2+y2)中,代数式的有 4 个.
【解答】解:根据代数式的定义,可知①、③、⑤、⑥都是代数式.
故答案为:4.
二.列代数式(共12小题)
8.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是( )
A.x+y
B.10xy
C.10(x+y)
D.10x+y
【解答】解:一个两位数,它的十位数字是x,个位数字是y,这个两位数10x+y.
故选:D.
9.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
【解答】解:根据题意知:17a+(20﹣17)(a+1.2)=(20a+3.6)(元)。
故选:D.
10.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园增加的面积为( )
A.a(b+x)
B.b(a+x)
C.ax
D.bx
【解答】解:∵长方形的花园长增加x,宽为b,
∴新的花园增加的面积为bx.
故选:D.
11.某产品的成本为A元,按成本加价四成作为定价销售,因季节原因按定价的六折出售,降价后的售价为( )元.
A.(60%﹣40%)A
B.60%×40%A
C.(1+40%)60%A
D.(1+40%)(1﹣60%)A
【解答】解:成本为A元,按成本加价四成作为定价销售即,定价为:(1+40%)A,
而降价后的售价按定价的六折,故降价后的售价为:(1+40%)60%A,
故A、B、D错误,
故选:C.
12.甲数是乙数的4倍少3,则下列说法正确的是( )
①设乙数为x,甲数为4x﹣3
②设甲数为x,乙数为x+3
③设甲数为x,乙数为(x+3)
④设甲数为x,乙数为(x﹣3)
A.①③
B.①②
C.②④
D.①④
【解答】解:甲数是乙数的4倍少3,
若设乙数为x,甲数为4x﹣3;若设甲数为x,则乙数的4倍是(x+3),所以乙数为(x+3),
∴①、③正确,
故B、C、D错误,
故选:A.
13.一个三位数,百位上的数字为x,十位上的数字比百位上的数字少3,个位上的数字是百位上的数字的2倍,这个三位数用含有x的代数式表示为( )
A.112x﹣30
B.100x﹣30
C.112x+30
D.102x+30
【解答】解:百位上的数字为x,十位上的数字为(x﹣3),个位上的数字为2x,
这个三位数是100x+10(x﹣3)+2x=100x+10x﹣30+2x=112x﹣30.
故选:A.
14.如果三角形底边上的高是6,底边长为x,那么三角形的面积y可以表示为
y=3x .
【解答】解:由题意得:y==3x.
故答案为:y=3x.
15.现有5元面值人民币m张,10元面值人民币n张,共有人民币 (5m+10n) 元(用含m、n的代数式表示).
【解答】解:由题意得5m+10n.
故答案为:(5m+10n).
16.如图是一块长方形场地ABCD,长AB=am,宽AD=bm,从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为 (a﹣2)(b﹣1) m2.(用含a,b的代数式表示)
【解答】解:将小路进行拼接,如图,
则草坪的长为(a﹣2)m,宽为(b﹣1)m,
草坪的面积为(a﹣2)(b﹣1)m2;
17.一条河的水流速度是3km/h,船在静水中的速度是vkm/h,则该船在这条河流中顺水行驶的速度为 (3+v) km/h.
【解答】解:顺水速度=静水船速+水流速度,
∴顺水速度为:(3+v)km/h.
故答案为:(3+v).
18.如图是一个娱乐场,其中半圆形休息区和长方形游泳池以外的地方都是绿地,已知娱乐场的长为3a,宽为2a,游泳池的长、宽分别是娱乐场长、宽的一半,且半圆形休息区的直径是娱乐场宽的一半,则绿地的面积为 a2 .(用含a的代数式表示,将结果化为最简)
【解答】解:由题意知游泳池的面积为a?a=a2,半圆形休息区面积为?π?()2=a2,
则绿地面积为2a?3a﹣a2﹣a2=a2,
故答案为:a2.
19.现有一块长方形菜地,长12米、宽10米.菜地中间欲铺设纵横两条路(图中空白部分)如图所示,横向道路的宽是纵向道路的宽的2倍,设纵向道路的宽是x米(x>0).
(1)填空:在图中,横向道路的宽是 2x 米(用含x的代数式表示).
(2)试求图中种菜部分的面积(用含x的代数式表示).
【解答】解:(1)设纵向道路的宽是x米,
∵横向道路的宽是纵向道路的宽的2倍,
∴横向道路的宽为2x米;
故答案是:2x;
(2)图中种菜部分的面积=12×2x+10x﹣x?2x=34x﹣2x2(平方米).
答:图中种菜部分的面积为(34x﹣2x2)平方米.
三.代数式求值(共12小题)
20.已知a﹣b=4,则代数式1+2a﹣2b的值为( )
A.9
B.5
C.7
D.﹣7
【解答】解:∵a﹣b=4,
∴1+2a﹣2b=1+2(a﹣b)=1+2×4=9,
故选:A.
21.若2y﹣3x=5,则代数式8+6x﹣4y的值是( )
A.﹣2
B.0
C.7
D.﹣3
【解答】解:8+6x﹣4y=8﹣2(2y﹣3x),
把2y﹣3x=5代入上式得,
原式=8﹣2×5=﹣2.
故选:A.
22.若a2+3a=1,则代数式5a2+15a﹣2的值为( )
A.0
B.1
C.2
D.3
【解答】解:∵a2+3a=1,
∴5a2+15a﹣2=5(a2+3a)﹣2=5×1﹣2=3,
故选:D.
23.按如图所示的运算程序,输出y的值为11的是( )
A.x=﹣3
B.x=0
C.x=5
D.x=﹣1
【解答】解:A,x=﹣3时,y=4.不符合题意.
B,x=0时,y=20,不符合题意.
C,x=5时,y=20,不符合题意.
D,x=﹣1,y=11,符合题意.
故选:D.
24.若a2﹣3b=1,则3a2﹣9b+2018= 2021 .
【解答】解:∵a2﹣3b=1,
∴3a2﹣9b+2018=3(a2﹣3b)+2018=3×1+2018=2021.
故答案为:2021
25.若m2+2m=2,则4m2+8m﹣3的值是
5 .
【解答】解:∵m2+2m=2,
∴4m2+8m=4(m2+2m)=4×2=8,
∴原式=8﹣3=5.
故答案为5.
26.已知a=1,则a2+4a+4= 9 .
【解答】解:∵a=1,
∴a2+4a+4=(a+2)2=(1+2)2=32=9.
故答案为:9.
27.如图是一个数字转换机的示意图,若x=3,则输出的结果为 7 .
【解答】解:根据题意可得,
输出结果为32﹣2=7.
故答案为:7.
28.已知代数式5x2﹣2x,请按照下列要求分别求值:
(1)当x=1时,代数式的值.
(2)当5x2﹣2x=0时,求x的值.
【解答】解:(1)当x=1时,5x2﹣2x=5﹣2=3;
(2)5x2﹣2x=0,
分解因式得:x(5x﹣2)=0,
可得x=0或5x﹣2=0,
解得:x=0或x=.
29.如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米)
(1)用含a,b的整式表示花坛的面积;
(2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元?
【解答】解:(1)(a+3b+a)(2a+b)﹣2a?3b
=4a2+8ab+3b2﹣6ab
=(4a2+2ab+3b2)(平方米).
答:花坛的面积是(4a2+2ab+3b2)平方米.
(2)当a=4,b=3时,
4a2+2ab+3b2
=4×42+4×2×3+3×32
=115(平方米),
115×500=57500(元).
答:建花坛的总工程费为57500元.
30.如图,已知长方形ABCD的宽AB=a,两个空白处圆的半径分别为a、b.
(1)用含字母的式子表示阴影部分的面积;
(2)当a=5,b=3时,阴影部分的面积是多少?
【解答】解:(1)阴影部分面积为:a(a+b)﹣﹣,
(2)当a=5,b=3时,阴影部分面积=5×(5+3)﹣﹣=40﹣.
31.如图,一个大长方形场地割出如图所示的“L”型阴影部分,请根据图中所给的数据,回答下列问题:
(1)用含x,y的代数式表示阴影部分的周长并化简.
(2)若x=3米,y=2米时,要给阴影部分场地围上价格每米7元的围栏作功能区,请计算围栏的造价.
【解答】解:(1)(2x+2y+x+2y)×2
=(3x+4y)×2
=(6x+8y).
(2)∵x=3米,y=2米,
∴(6x+8y)×7
=(6×3+8×2)×7
=(18+16)×7
=34×7
=238(元).
答:围栏的造价是238元
2
/
2
一.代数式(共7小题)
1.下列代数式符合书写要求的是( )
A.7xy
B.ab×9
C.
D.1÷a
2.代数式x﹣y2的意义为( )
A.x的平方与y的平方的差
B.x与y的相反数的平方差
C.x与y的差的平方
D.x减去y的平方的差
3.下列代数式符合规范书写要求的是( )
A.﹣1x
B.1xy
C.0.3÷x
D.﹣a
4.下列式子,代数式有( )
A.6个
B.5个
C.4个
D.3个
5.下列说法中,正确的是( )
A.表示x,y,3,的积的代数式为3xy
B.a是代数式,1不是代数式
C.的意义是a与3的差除b的商
D.m,n两数的差的平方与m,n两数积的2倍的和表示为(m﹣n)2+2mn
6.已知一个等边三角形的边长为a,则3a所表示的实际意义是
.
7.在下列各式:①π﹣3;②ab=ba;③x;④2m﹣1>0:⑤;⑥8(x2+y2)中,代数式的有
个.
二.列代数式(共12小题)
8.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是( )
A.x+y
B.10xy
C.10(x+y)
D.10x+y
9.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
10.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园增加的面积为( )
A.a(b+x)
B.b(a+x)
C.ax
D.bx
11.某产品的成本为A元,按成本加价四成作为定价销售,因季节原因按定价的六折出售,降价后的售价为( )元.
A.(60%﹣40%)A
B.60%×40%A
C.(1+40%)60%A
D.(1+40%)(1﹣60%)A
12.甲数是乙数的4倍少3,则下列说法正确的是( )
①设乙数为x,甲数为4x﹣3
②设甲数为x,乙数为x+3
③设甲数为x,乙数为(x+3)
④设甲数为x,乙数为(x﹣3)
A.①③
B.①②
C.②④
D.①④
13.一个三位数,百位上的数字为x,十位上的数字比百位上的数字少3,个位上的数字是百位上的数字的2倍,这个三位数用含有x的代数式表示为( )
A.112x﹣30
B.100x﹣30
C.112x+30
D.102x+30
14.如果三角形底边上的高是6,底边长为x,那么三角形的面积y可以表示为
.
15.现有5元面值人民币m张,10元面值人民币n张,共有人民币
元(用含m、n的代数式表示).
16.如图是一块长方形场地ABCD,长AB=am,宽AD=bm,从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为
m2.(用含a,b的代数式表示)
17.一条河的水流速度是3km/h,船在静水中的速度是vkm/h,则该船在这条河流中顺水行驶的速度为
km/h.
18.如图是一个娱乐场,其中半圆形休息区和长方形游泳池以外的地方都是绿地,已知娱乐场的长为3a,宽为2a,游泳池的长、宽分别是娱乐场长、宽的一半,且半圆形休息区的直径是娱乐场宽的一半,则绿地的面积为
.(用含a的代数式表示,将结果化为最简)
19.现有一块长方形菜地,长12米、宽10米.菜地中间欲铺设纵横两条路(图中空白部分)如图所示,横向道路的宽是纵向道路的宽的2倍,设纵向道路的宽是x米(x>0).
(1)填空:在图中,横向道路的宽是
米(用含x的代数式表示).
(2)试求图中种菜部分的面积(用含x的代数式表示).
三.代数式求值(共12小题)
20.已知a﹣b=4,则代数式1+2a﹣2b的值为( )
A.9
B.5
C.7
D.﹣7
21.若2y﹣3x=5,则代数式8+6x﹣4y的值是( )
A.﹣2
B.0
C.7
D.﹣3
22.若a2+3a=1,则代数式5a2+15a﹣2的值为( )
A.0
B.1
C.2
D.3
23.按如图所示的运算程序,输出y的值为11的是( )
A.x=﹣3
B.x=0
C.x=5
D.x=﹣1
24.若a2﹣3b=1,则3a2﹣9b+2018=
.
25.若m2+2m=2,则4m2+8m﹣3的值是
.
26.已知a=1,则a2+4a+4=
.
27.如图是一个数字转换机的示意图,若x=3,则输出的结果为
.
28.已知代数式5x2﹣2x,请按照下列要求分别求值:
(1)当x=1时,代数式的值.
(2)当5x2﹣2x=0时,求x的值.
29.如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米)
(1)用含a,b的整式表示花坛的面积;
(2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元?
30.如图,已知长方形ABCD的宽AB=a,两个空白处圆的半径分别为a、b.
(1)用含字母的式子表示阴影部分的面积;
(2)当a=5,b=3时,阴影部分的面积是多少?
31.如图,一个大长方形场地割出如图所示的“L”型阴影部分,请根据图中所给的数据,回答下列问题:
(1)用含x,y的代数式表示阴影部分的周长并化简.
(2)若x=3米,y=2米时,要给阴影部分场地围上价格每米7元的围栏作功能区,请计算围栏的造价.
3.2代数式同步练习
参考答案与试题解析
一.代数式(共7小题)
1.下列代数式符合书写要求的是( )
A.7xy
B.ab×9
C.
D.1÷a
【解答】解:A、系数应为假分数,原书写错误,故此选项不符合题意;
B、系数应写在字母的前面,原书写错误,故此选项不符合题意;
C、符合要求,故此选项符合题意;
D、应写成分式的形式,原书写错误,故此选项不符合题意;
故选:C.
2.代数式x﹣y2的意义为( )
A.x的平方与y的平方的差
B.x与y的相反数的平方差
C.x与y的差的平方
D.x减去y的平方的差
【解答】解:在含有幂的运算中,先算y的平方,再计算x和y2的差.
故选:D.
3.下列代数式符合规范书写要求的是( )
A.﹣1x
B.1xy
C.0.3÷x
D.﹣a
【解答】解:A、原书写错误,应该写成﹣x,故此选项不符合题意;
B、原书写错误,应写成xy,故此选项不符合题意;
C、原书写错误,应写成,故此选项不符合题意;
D、原书写正确,故此选项符合题意.
故选:D.
4.下列式子,代数式有( )
A.6个
B.5个
C.4个
D.3个
【解答】解:代数式有:+b,0,d,8+y,共有4个.
故选:C.
5.下列说法中,正确的是( )
A.表示x,y,3,的积的代数式为3xy
B.a是代数式,1不是代数式
C.的意义是a与3的差除b的商
D.m,n两数的差的平方与m,n两数积的2倍的和表示为(m﹣n)2+2mn
【解答】解:A、表示x,y,3,的积的代数式为xy,原说法错误,故此选项不符合题意;
B、a是代数式,1也是代数式,原说法错误,故此选项不符合题意;
C、的意义是:a与3的差除以b的商,原说法错误,故此选项不符合题意;
D、m,n两数的差的平方与m,n两数积的2倍的和表示为(m﹣n)2+2mn,原说法正确,故此选项符合题意.
故选:D.
6.已知一个等边三角形的边长为a,则3a所表示的实际意义是 这个等边三角形的周长 .
【解答】解:因为等边三角形的边长为a,
所以3a所表示的实际意义是这个三角形的周长.
故答案为这个等边三角形的周长.
7.在下列各式:①π﹣3;②ab=ba;③x;④2m﹣1>0:⑤;⑥8(x2+y2)中,代数式的有 4 个.
【解答】解:根据代数式的定义,可知①、③、⑤、⑥都是代数式.
故答案为:4.
二.列代数式(共12小题)
8.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是( )
A.x+y
B.10xy
C.10(x+y)
D.10x+y
【解答】解:一个两位数,它的十位数字是x,个位数字是y,这个两位数10x+y.
故选:D.
9.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
【解答】解:根据题意知:17a+(20﹣17)(a+1.2)=(20a+3.6)(元)。
故选:D.
10.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园增加的面积为( )
A.a(b+x)
B.b(a+x)
C.ax
D.bx
【解答】解:∵长方形的花园长增加x,宽为b,
∴新的花园增加的面积为bx.
故选:D.
11.某产品的成本为A元,按成本加价四成作为定价销售,因季节原因按定价的六折出售,降价后的售价为( )元.
A.(60%﹣40%)A
B.60%×40%A
C.(1+40%)60%A
D.(1+40%)(1﹣60%)A
【解答】解:成本为A元,按成本加价四成作为定价销售即,定价为:(1+40%)A,
而降价后的售价按定价的六折,故降价后的售价为:(1+40%)60%A,
故A、B、D错误,
故选:C.
12.甲数是乙数的4倍少3,则下列说法正确的是( )
①设乙数为x,甲数为4x﹣3
②设甲数为x,乙数为x+3
③设甲数为x,乙数为(x+3)
④设甲数为x,乙数为(x﹣3)
A.①③
B.①②
C.②④
D.①④
【解答】解:甲数是乙数的4倍少3,
若设乙数为x,甲数为4x﹣3;若设甲数为x,则乙数的4倍是(x+3),所以乙数为(x+3),
∴①、③正确,
故B、C、D错误,
故选:A.
13.一个三位数,百位上的数字为x,十位上的数字比百位上的数字少3,个位上的数字是百位上的数字的2倍,这个三位数用含有x的代数式表示为( )
A.112x﹣30
B.100x﹣30
C.112x+30
D.102x+30
【解答】解:百位上的数字为x,十位上的数字为(x﹣3),个位上的数字为2x,
这个三位数是100x+10(x﹣3)+2x=100x+10x﹣30+2x=112x﹣30.
故选:A.
14.如果三角形底边上的高是6,底边长为x,那么三角形的面积y可以表示为
y=3x .
【解答】解:由题意得:y==3x.
故答案为:y=3x.
15.现有5元面值人民币m张,10元面值人民币n张,共有人民币 (5m+10n) 元(用含m、n的代数式表示).
【解答】解:由题意得5m+10n.
故答案为:(5m+10n).
16.如图是一块长方形场地ABCD,长AB=am,宽AD=bm,从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为 (a﹣2)(b﹣1) m2.(用含a,b的代数式表示)
【解答】解:将小路进行拼接,如图,
则草坪的长为(a﹣2)m,宽为(b﹣1)m,
草坪的面积为(a﹣2)(b﹣1)m2;
17.一条河的水流速度是3km/h,船在静水中的速度是vkm/h,则该船在这条河流中顺水行驶的速度为 (3+v) km/h.
【解答】解:顺水速度=静水船速+水流速度,
∴顺水速度为:(3+v)km/h.
故答案为:(3+v).
18.如图是一个娱乐场,其中半圆形休息区和长方形游泳池以外的地方都是绿地,已知娱乐场的长为3a,宽为2a,游泳池的长、宽分别是娱乐场长、宽的一半,且半圆形休息区的直径是娱乐场宽的一半,则绿地的面积为 a2 .(用含a的代数式表示,将结果化为最简)
【解答】解:由题意知游泳池的面积为a?a=a2,半圆形休息区面积为?π?()2=a2,
则绿地面积为2a?3a﹣a2﹣a2=a2,
故答案为:a2.
19.现有一块长方形菜地,长12米、宽10米.菜地中间欲铺设纵横两条路(图中空白部分)如图所示,横向道路的宽是纵向道路的宽的2倍,设纵向道路的宽是x米(x>0).
(1)填空:在图中,横向道路的宽是 2x 米(用含x的代数式表示).
(2)试求图中种菜部分的面积(用含x的代数式表示).
【解答】解:(1)设纵向道路的宽是x米,
∵横向道路的宽是纵向道路的宽的2倍,
∴横向道路的宽为2x米;
故答案是:2x;
(2)图中种菜部分的面积=12×2x+10x﹣x?2x=34x﹣2x2(平方米).
答:图中种菜部分的面积为(34x﹣2x2)平方米.
三.代数式求值(共12小题)
20.已知a﹣b=4,则代数式1+2a﹣2b的值为( )
A.9
B.5
C.7
D.﹣7
【解答】解:∵a﹣b=4,
∴1+2a﹣2b=1+2(a﹣b)=1+2×4=9,
故选:A.
21.若2y﹣3x=5,则代数式8+6x﹣4y的值是( )
A.﹣2
B.0
C.7
D.﹣3
【解答】解:8+6x﹣4y=8﹣2(2y﹣3x),
把2y﹣3x=5代入上式得,
原式=8﹣2×5=﹣2.
故选:A.
22.若a2+3a=1,则代数式5a2+15a﹣2的值为( )
A.0
B.1
C.2
D.3
【解答】解:∵a2+3a=1,
∴5a2+15a﹣2=5(a2+3a)﹣2=5×1﹣2=3,
故选:D.
23.按如图所示的运算程序,输出y的值为11的是( )
A.x=﹣3
B.x=0
C.x=5
D.x=﹣1
【解答】解:A,x=﹣3时,y=4.不符合题意.
B,x=0时,y=20,不符合题意.
C,x=5时,y=20,不符合题意.
D,x=﹣1,y=11,符合题意.
故选:D.
24.若a2﹣3b=1,则3a2﹣9b+2018= 2021 .
【解答】解:∵a2﹣3b=1,
∴3a2﹣9b+2018=3(a2﹣3b)+2018=3×1+2018=2021.
故答案为:2021
25.若m2+2m=2,则4m2+8m﹣3的值是
5 .
【解答】解:∵m2+2m=2,
∴4m2+8m=4(m2+2m)=4×2=8,
∴原式=8﹣3=5.
故答案为5.
26.已知a=1,则a2+4a+4= 9 .
【解答】解:∵a=1,
∴a2+4a+4=(a+2)2=(1+2)2=32=9.
故答案为:9.
27.如图是一个数字转换机的示意图,若x=3,则输出的结果为 7 .
【解答】解:根据题意可得,
输出结果为32﹣2=7.
故答案为:7.
28.已知代数式5x2﹣2x,请按照下列要求分别求值:
(1)当x=1时,代数式的值.
(2)当5x2﹣2x=0时,求x的值.
【解答】解:(1)当x=1时,5x2﹣2x=5﹣2=3;
(2)5x2﹣2x=0,
分解因式得:x(5x﹣2)=0,
可得x=0或5x﹣2=0,
解得:x=0或x=.
29.如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米)
(1)用含a,b的整式表示花坛的面积;
(2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元?
【解答】解:(1)(a+3b+a)(2a+b)﹣2a?3b
=4a2+8ab+3b2﹣6ab
=(4a2+2ab+3b2)(平方米).
答:花坛的面积是(4a2+2ab+3b2)平方米.
(2)当a=4,b=3时,
4a2+2ab+3b2
=4×42+4×2×3+3×32
=115(平方米),
115×500=57500(元).
答:建花坛的总工程费为57500元.
30.如图,已知长方形ABCD的宽AB=a,两个空白处圆的半径分别为a、b.
(1)用含字母的式子表示阴影部分的面积;
(2)当a=5,b=3时,阴影部分的面积是多少?
【解答】解:(1)阴影部分面积为:a(a+b)﹣﹣,
(2)当a=5,b=3时,阴影部分面积=5×(5+3)﹣﹣=40﹣.
31.如图,一个大长方形场地割出如图所示的“L”型阴影部分,请根据图中所给的数据,回答下列问题:
(1)用含x,y的代数式表示阴影部分的周长并化简.
(2)若x=3米,y=2米时,要给阴影部分场地围上价格每米7元的围栏作功能区,请计算围栏的造价.
【解答】解:(1)(2x+2y+x+2y)×2
=(3x+4y)×2
=(6x+8y).
(2)∵x=3米,y=2米,
∴(6x+8y)×7
=(6×3+8×2)×7
=(18+16)×7
=34×7
=238(元).
答:围栏的造价是238元
2
/
2
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
