2021-2022学年九年级上册人教版数学25.2用列举法求概率教学课件(47张ppt)
文档属性
| 名称 | 2021-2022学年九年级上册人教版数学25.2用列举法求概率教学课件(47张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 18:54:39 | ||
图片预览










文档简介
第1课时
25.2 用列举法求概率
九年级上册 RJ
初中数学
知识回顾
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为:
概率的计算
P(A)=????????
?
1.知道“直接列举法”和“列表法”求随机事件的概率的适用条件.
2.会正确“列表”表示出所有可能出现的结果.
3.知道如何利用“列表法”求随机事件的概率.
学习目标
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1) 两枚硬币全部正面向上;
(2) 两枚硬币全部反面向上;
(3) 一枚硬币正面向上、一枚硬币反面向上.
分析:“掷两枚硬币”所有结果如下.
正正
反反
反正
正反
课堂导入
解:列举抛掷两枚硬币所能产生的所有结果,它们是:
(1)其中两枚硬币全部正面向上(记为事件A)的结果有1种,即“正正”,所以
(2) 两枚硬币全部反面向上(记为事件B)的结果有1种,即“正反”,所以
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C) 的结果共有两种,即“反正”“正反”所以
????????=14.
?
????(????)=14
?
????(????)=12.
?
技巧点拨:先列出硬币落地后所有可能出现的结果,再分别数出各种事件发生的结果数,最后带入概率公式求解。
正正,正反,反正,反反.
只需比较老师赢和学生赢的概率是否一样就可以了.
P(学生赢)= 24=12 .
?
一正一反的结果
P(老师赢) =24=12 .
?
同时向空中抛掷两枚质地均匀的硬币,若落地后一正一反,老师赢;若落地后两面一样,学生赢. 那么这个游戏公平吗?
所以这个游戏公平.
答:因为P(老师赢) =P(学生赢),
?
2种
两面一样的结果
2种
一共有结果
4种
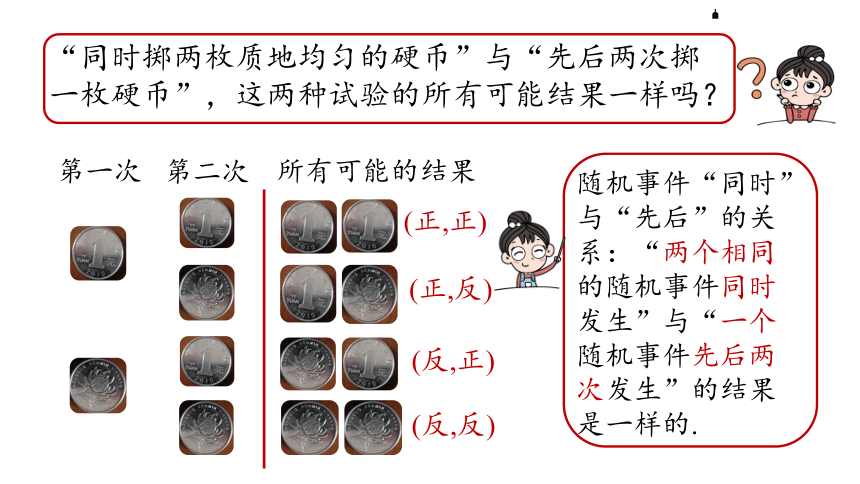
第一次
第二次
所有可能的结果
(正,正)
(正,反)
(反,正)
(反,反)
“同时掷两枚质地均匀的硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
当事件涉及的对象比较单一且出现的等可能结果数目较少时,就可以直接列举出所有等可能的结果,再利用概率公式P(A)=? (在一次试验中,有n种等可能的结果,事件A包含其中的m种结果)求事件发生的概率的方法,我们称为直接列举法.
?
知识点1
新知探究
注意:(1)为保证结果不重不漏,直接列举时,要有一定的顺序性.
(2)用列举法求概率的前提条件有两个:
①所有可能出现的结果是有限个;
②每个结果出现的可能性相等.
(3)所求概率是一个准确数,一般用分数表示.
????????
?
例1 若我们把十位上的数字比个位和百位上数字都小的三位数称为“V数”, 如756, 326 , 那么从2, 3, 4这三个数字组成的无重复数
字的三位数中任意抽取一个数, 则该数是“V数”的概率为 .
13
?
解:由2, 3, 4这三个数字组成的无重复数字的所有三位数为234, 243, 324, 342, 432, 423,共6种情况, 而“V”数有324和423,共2种情况,
故从2, 3, 4这三个数字组成的无重复数字的三位数中任意抽取一个数, 则该数是“V”数的概率为 26=13 .
?
跟踪训练
新知探究
分析:求解本题的关键是不重不漏地列举出由2,3,4组成的无重复数字的所有的三位数.
知识点2
新知探究
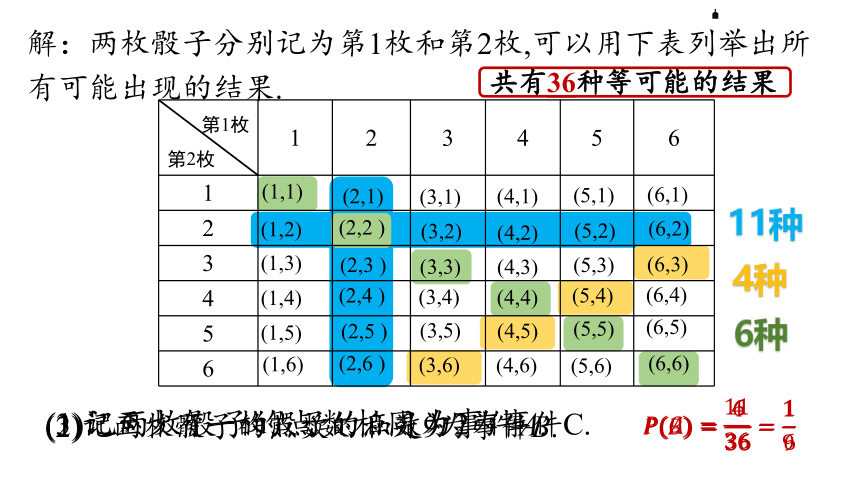
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
除了直接列举法,还有什么办法能不重不漏地列举出所有可能出现的结果呢?
第1枚
第2枚
1
2
3
4
5
6
1
2
3
4
5
6
解:两枚骰子分别记为第1枚和第2枚,可以用下表列举出所有可能出现的结果.
(1,3)
(1,5)
(1,1)
(1,2)
(1,4)
(1,6)
(2,1)
(2,3 )
(2,4 )
(2,5 )
(2,6 )
(2,2 )
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
(1)记两枚骰子的点数相同为事件A.
????(????)=636=16
?
(2)记两枚骰子的点数的和是9为事件B.
????(????)=1136
?
????(????)=436=19
?
(3)记至少有一枚骰子的点数为2为事件C.
共有36种等可能的结果
6种
4种
11种
当一次试验涉及两个因素,并且可能出现的等可能结果数目较多时,为不重不漏地列出所有等可能的结果,通常采用列表法。
包括两种情况:
(1)同时进行两种相同的操作;
(2)先后进行两次相同的操作.
①列表
②通过表格确定公式中m, n的值
③利用P(A)= 计算事件的概率
????????
?
运用列表法求概率的步骤
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况
列表法中表格构造特点:
列表时,列举顺序不能颠倒.
例2 利用如图所示的两个转盘玩配紫色游戏(红色和蓝色可以配成紫色),两个转盘各转一次,则指针所指区域可以配成紫色的概率为多少?
跟踪训练
新知探究
{5940675A-B579-460E-94D1-54222C63F5DA}
红
黄
蓝
蓝
(红,蓝)
(黄,蓝)
(蓝,蓝)
黄
(红,黄)
(黄,黄)
(蓝,黄)
红
(红,红)
(黄,红)
(蓝,红)
黄
(红,黄)
(黄,黄)
(蓝,黄)
红
(红,红)
(黄,红)
(蓝,红)
由上表可知,共有15种等可能的结果,其中可以配成紫色的结果有3种,所以P(可以配成紫色) = 315=15 .
?
解:列表如下.
转盘(2) 颜色
转盘(1) 颜色
第1次
第2次
1
2
3
4
1
2
3
4
(1,3)
(1,1)
(2,1)
(3,1)
(4,1)
(1,2)
(2,2 )
(3,2)
(4,2)
(2,3 )
(3,3)
(4,3)
(1,4)
(2,4 )
(3,4)
(4,4)
2.一个不透明的袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机地摸取一个小球然后放回,再随机地摸出一个小球.求下列事件的概率:
(1)两次取出的小球标号相同;
(2)两次取出的小球标号和等于4.
解:(1)记两次取出的小球标号 相同为事件A.
?(2)记两次取出的小球标号和等于4为事件B.
????(????)=416=14
?
????(????)=316
?
1.把一副普通扑克牌中的13张黑桃牌洗匀后正面向下放在桌子上,从中随机抽取一张,求下列事件的概率:
(1) 抽出的牌是黑桃6;
(2) 抽出的牌是黑桃10;
(3) 抽出的牌带有人像;
(4) 抽出的牌上的数小于5;
(5) 抽出的牌的花色是黑桃.
113
?
113
?
313
?
413
?
1
?
随堂练习
2.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别.随机摸出一个小球后,放回并摇匀,再随机摸出一个.求下列事件的概率:
(1) 第一次摸到红球,第二次摸到绿球;
(2) 两次都摸到相同颜色的小球;
(3) 两次摸到的小球中一个绿球、一个红球.
解:所有等可能的结果为红红、红绿、绿红、绿绿,共4种情况,
第一次摸到红球,第二次摸到绿球的情况有1种,则????(第一次摸到红球,第二次摸到绿球)=14 .
两次都摸到相同颜色的小球的情况有2种,则
????(两次都摸到相同颜色的小球)= 24=12 .
(3) 两次摸到的球中一个绿球、一个红球的情况共2种,则????(两次摸到的小球中一个绿球、一个红球)= 24=12 .
?
3.五张形状、大小、背面完全相同的卡片上分别标有数-3,
-1,0,1,2,将卡片洗匀后背面朝上放在桌面上,从中任意抽
取两张,则所抽卡片上的数的积是正数的概率是多少?
-3
-1
0
1
2
-3
3
0
-3
-6
-1
3
0
-3
6
0
0
0
0
0
1
-3
-1
0
2
2
-6
-2
0
2
积
解:列表如下
“不放回”试验反映在表格上就是去掉表格中一条对角线上的所有结果
为什么对角线上的数据没列出来呢?
隐含“不放回”.
第1次
第2次
共 种结果
20
积是正数: 种
4
P(所抽卡片上的数的积是正数) =
420
?
=15
?
易错警示:混淆“放回”与“不放回”致错
本题是不放回试验,不可能抽到两张数相同的卡片,所以列表格里要排除掉两张卡片上的数相同的情况.
列举法
关键
常用
方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验.
基本步骤
① 列表;② 确定m,n的值; ③代入概率公式计算.
正确列举出所有等
可能出现的结果.
确保试验中每种结果出现的可能性大小相等.
前提条件
课堂小结
A. B. C. D.
C
对接中考
1.(2020?北京中考)不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
解:列表如下:
{5940675A-B579-460E-94D1-54222C63F5DA}
1
2
1
2
3
2
3
4
由表可知,共有4种等可能的结果,
其中两次记录的数字之和为3的有2种结果,
所以两次记录的数字之和为3的概率为
14
?
13
?
23
?
12
?
24=12
?
故选:C
2.有6张看上去无差别的卡片,上面分别写着1, 2, 3, 4, 5, 6.随机抽取1张后,放回并混在一起,再随机抽取1张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
解:由题意得两次抽取共有36种等可能出现的结果,
第二次取出的数字能够整除第一次取出的数字的结果
有14种,即有(1,1), (2,1), (2,2), (3,1), (3,3), (4,1), (4,2), (4,4),(5,1),(5,5),(6,1),(6,2),(6,3),(6,6) ,
所以所求概率为 .
1436=718
?
3.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球然后放回,再随机摸出一个小球,求下列事件的概率.
两次摸出的小球的标号相同;
(2) 两次摸出的小球标号的和等于4.
(2) 两次取出的小球标号的和等于4的情况有三种,即(3,1),(1,3),(2,2) ,所以
P(两次摸出的小球标号的和等于4)=的概率为 316 .
?
解:由题意得随机地摸出一个小球,然后放回,再随机地摸出一个小球,共有16种等可能的结果,
(1) 其中两次摸出的小球标号相同的有(1,1),(2,2),(3,3),(4,4),共4种,所以
P(两次摸出的小球标号相同)= 416=14 .
?
第2课时
25.2 用列举法求概率
九年级上册 RJ
初中数学
上节课我们学习了哪些求概率的方法?
1.直接列举法.
2.列表法.
知识回顾
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.
学习目标
课堂导入
小红上学要经过三个十字路口,每个路口遇到红绿灯,红、黄、绿三色灯亮的的可能性都相等,小红希望上学时经过的每个路口都是绿灯,此事件发生的概率是多少?
这个问题能用直接列表法和列表法解决吗?有什么简单的解决办法吗?
第2路口
第1路口
红
绿
黄
红
绿
黄
第3路口
一共有27种情况,每种情况发生的可能性相等,
其中三个路口都为绿灯的情况只有 种,
所以3个路口都为绿灯的概率为
127
?
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
红
红
红
红
黄
红
红
绿
黄
红
绿
红
绿
绿
红
绿
红
绿
黄
红
绿
黄
黄
绿
黄
绿
黄
红
黄
黄
红
红
红
黄
红
红
黄
黄
红
黄
绿
红
绿
黄
绿
绿
红
绿
绿
黄
绿
绿
绿
绿
黄
红
绿
黄
黄
绿
黄
绿
黄
绿
红
黄
绿
黄
黄
绿
绿
黄
黄
红
黄
黄
黄
黄
黄
绿
解:根据题意画树状图如下:
1
以上用树状图的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法叫做画树状图法.
画树状图法求概率的适用条件是什么呢?
当一次试验涉及两个或更多个因素时,为了不重不漏地列出所有等可能的结果,通常采用画树状图法.
知识点
新知探究
数出所有事件出现的结果数n和A事件出现的结果数m.
代入公式P(A)= 计算概率
用树状图法求概率的“四个步骤”
????????
?
①定
②画
③数
④算
确定该试验的几个步骤、顺序、每一步可能产生的结果.
列举每一步可能出现的结果,得到树状图.
例1 甲口袋中有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1) 取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2) 取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
跟踪训练
新知探究
甲
乙
丙
A
B
C
E
D
C
E
D
H I
H I
H I
H I
H I
H I
解:根据题意,可以画出如下的树状图:
A
C
H
A
C
I
A
E
I
B
C
H
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
A
D
H
A
D
I
A
E
H
由树状图可以看出,所有可能出现的结果共有12种,
即ACH,ACI,ADH,ADI,AEH,AEI,BCH,BCI,BDH,BDI,BEH, BEI,
这些结果出现的可能性相等.
(2)全是辅音字母的结果共有 种,
全部为元音字母的结果只有 种,
(1)只有1个元音字母的结果有 种,
所以P(1个元音)= 512 .
?
有2个元音字母的结果有 种,
所以P(2个元音)= 412=13 .
?
所以P(3个元音)= 112 .
?
所以P(3个辅音)= 212=16.
?
5
1
4
2
用列举法求事件的概率的方法:
直接列举法;
列表法;
画树状图法.
注意:用列举法求概率时,各种结果出现的可能性必须相同,并要不重不漏地列举出所有等可能的结果.
什么时候该用列表法什么时候该用画树状图法呢?
当试验包含两步时,既可以用列表法有又可以用画树状图法;当试验包含三步或三步以上时,不能用列表法,用画树状图法比较方便.
例2 现有A,B,C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包、一个糖包和一个韭菜包, C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那么老师选的包子全部是酸菜包的概率是多少?
解:根据题意,画出树状图如下
由树状图得,所有等可能出现的结果有 ,
P(老师选的包子全部是酸菜包)= 218=19 .
?
A盘
B盘
C盘
酸
糖
韭
酸
酸
糖
酸
酸
酸
酸
糖
韭
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
糖
韭
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
韭
酸
糖
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
韭
酸
糖
糖
酸
酸
糖
酸
糖
糖
糖
酸
糖
糖
糖
韭
糖
糖
酸
酸
酸
2种
所以
选的包子全部是酸菜包的结果有 ,
18种
1.如图(1)是一电路AB的开关控制,任意闭合两个开关,可能会使电路形成通路.
(1) 补全如图(2)所示的树状图;
(2) 求使电路形成通路的概率.
随堂练习
分析:此电路形成通路的条件是开关a,b闭合其中的一个,开关c,d,e闭合其中的一个,因此,当同时闭合的两个开关中一个是a或b,另一个是c或d或e时,电路才形成通路。
解:(1) 补全树状图如图所示.
所以P(电路形成通路)= .
a
不通
通
通
通
b
不通
通
通
通
c
通
通
不通
不通
e
通
通
不通
不通
d
通
通
不通
不通
c
b
d
e
b
a
c
e
b
a
d
e
c
a
d
e
b
a
c
d
1220=35
?
(2)由树状图可知,所有等可能出现的结果有 种,
其中能使电路形成通路的结果有 种,
12
20
2.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1) 三辆车全部继续直行;
(2) 两车向右,一车向左;
(3) 至少两车向左.
分析:包括两车向左、三车向左,其中两车向左又可分为两车向左一车向右、两车向左一车直行两种情况.
第一辆
左
右
第二辆
第三辆
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
(1) P(全部继续直行) = 127 ;
?
(2) P(两车向右,一车向左) = 327=19 ;
?
(3) P(至少两车向左) = 727 .
?
左
右
直
左
右
直
左直右
左直右
左直右
解:根据题意,画树状图如下:
左
直
直
左
左
左
直
左
左
右
左
直
左
左
左
左
直
右
左
右
左
左
右
右
左
右
直
直
左
左
直
直
左
直
直
直
直
直
右
直
右
直
左
直
左
直
右
直
直
右
右
右
左
左
直
左
右
右
左
右
右
直
左
右
直
直
右
直
左
右
右
左
右
右
直
右
右
右
右
右
直
树状图
步骤
适用条件
试验涉及两个或更多个因素时用此方法.
注意
①弄清试验涉及的因素个数或试验步骤分几步;
③利用概率公式进行计算.
①确定试验的步骤、每一步产生的结果;
②在树状图下面写出所有等可能的结果;
②在摸球试验中一定要弄清“放回”还是“不放回”.
课堂小结
③数出所有事件出现的结果数n和A事件出现的结果数m.
对接中考
1.(2020?玉林中考)经过人民中路十字路口红绿灯处的两辆汽车,可能直行,也可能向左转,如果这两种可能性大小相同,则至少有一辆向左转的概率是 .
解析:画树状图如下:
由树状图知,共有4种等可能的结果,
34
?
第一辆
直行
左转
直行
左转
直行
左转
第二辆
34
?
所以至少有一辆向左转的概为 .
其中至少有一辆向左转的结果有3种,
2.小颖和小明用如图所示的两个转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可配成紫色,此时小颖得2分,否则小明得1分,这个游戏公平吗?若你认为不公平,如何修改规则才能使游戏对双方公平?
解:画出树状图如图所示:
游戏规则可改为:若配成紫色,则小颖得2分;若两次转到相同颜色,则小明得2分;配成其他颜色两人均不得分.(修改方式不唯一)
红
黄
黄
红
红
黄
黄
蓝
A转盘
B转盘
由树状图可知,一共有6种等可能的结果,
其中能配成紫色的有1种,
所以能配成紫色的概率是 16 ,
?
不能配成紫色的概率是 56.
?
因为 16×2 < 56 ,
?
所以这个游戏不公平.
技巧点拨:保证游戏规则公平的两种途径①使用参与游戏各方获胜的概率相同;②参与游戏的各方获胜的概率不同时,可以通过控制分值使各方获胜概率与分值的乘积相等.
易错警示:本题易因忽略等可能性出错.B转盘虽然只有两种颜色,但因为红色和黄色所占的比例不一样,所以要使可能性相同,黄色应分成两份.
3.(2020.南州)某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是 .
解:画出树状图得,
其中出场顺序恰好是甲、
乙、丙的只有1种结果,
甲
丙
乙
丙
乙
丙
甲
乙
甲
丙
乙
甲
丙
甲
乙
16
?
16
?
第1个
第2个
第3个
共有6种等可能的结果,
∴出场顺序恰好是甲、乙、丙的概率为 .
25.2 用列举法求概率
九年级上册 RJ
初中数学
知识回顾
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为:
概率的计算
P(A)=????????
?
1.知道“直接列举法”和“列表法”求随机事件的概率的适用条件.
2.会正确“列表”表示出所有可能出现的结果.
3.知道如何利用“列表法”求随机事件的概率.
学习目标
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1) 两枚硬币全部正面向上;
(2) 两枚硬币全部反面向上;
(3) 一枚硬币正面向上、一枚硬币反面向上.
分析:“掷两枚硬币”所有结果如下.
正正
反反
反正
正反
课堂导入
解:列举抛掷两枚硬币所能产生的所有结果,它们是:
(1)其中两枚硬币全部正面向上(记为事件A)的结果有1种,即“正正”,所以
(2) 两枚硬币全部反面向上(记为事件B)的结果有1种,即“正反”,所以
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C) 的结果共有两种,即“反正”“正反”所以
????????=14.
?
????(????)=14
?
????(????)=12.
?
技巧点拨:先列出硬币落地后所有可能出现的结果,再分别数出各种事件发生的结果数,最后带入概率公式求解。
正正,正反,反正,反反.
只需比较老师赢和学生赢的概率是否一样就可以了.
P(学生赢)= 24=12 .
?
一正一反的结果
P(老师赢) =24=12 .
?
同时向空中抛掷两枚质地均匀的硬币,若落地后一正一反,老师赢;若落地后两面一样,学生赢. 那么这个游戏公平吗?
所以这个游戏公平.
答:因为P(老师赢) =P(学生赢),
?
2种
两面一样的结果
2种
一共有结果
4种
第一次
第二次
所有可能的结果
(正,正)
(正,反)
(反,正)
(反,反)
“同时掷两枚质地均匀的硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
当事件涉及的对象比较单一且出现的等可能结果数目较少时,就可以直接列举出所有等可能的结果,再利用概率公式P(A)=? (在一次试验中,有n种等可能的结果,事件A包含其中的m种结果)求事件发生的概率的方法,我们称为直接列举法.
?
知识点1
新知探究
注意:(1)为保证结果不重不漏,直接列举时,要有一定的顺序性.
(2)用列举法求概率的前提条件有两个:
①所有可能出现的结果是有限个;
②每个结果出现的可能性相等.
(3)所求概率是一个准确数,一般用分数表示.
????????
?
例1 若我们把十位上的数字比个位和百位上数字都小的三位数称为“V数”, 如756, 326 , 那么从2, 3, 4这三个数字组成的无重复数
字的三位数中任意抽取一个数, 则该数是“V数”的概率为 .
13
?
解:由2, 3, 4这三个数字组成的无重复数字的所有三位数为234, 243, 324, 342, 432, 423,共6种情况, 而“V”数有324和423,共2种情况,
故从2, 3, 4这三个数字组成的无重复数字的三位数中任意抽取一个数, 则该数是“V”数的概率为 26=13 .
?
跟踪训练
新知探究
分析:求解本题的关键是不重不漏地列举出由2,3,4组成的无重复数字的所有的三位数.
知识点2
新知探究
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
除了直接列举法,还有什么办法能不重不漏地列举出所有可能出现的结果呢?
第1枚
第2枚
1
2
3
4
5
6
1
2
3
4
5
6
解:两枚骰子分别记为第1枚和第2枚,可以用下表列举出所有可能出现的结果.
(1,3)
(1,5)
(1,1)
(1,2)
(1,4)
(1,6)
(2,1)
(2,3 )
(2,4 )
(2,5 )
(2,6 )
(2,2 )
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
(1)记两枚骰子的点数相同为事件A.
????(????)=636=16
?
(2)记两枚骰子的点数的和是9为事件B.
????(????)=1136
?
????(????)=436=19
?
(3)记至少有一枚骰子的点数为2为事件C.
共有36种等可能的结果
6种
4种
11种
当一次试验涉及两个因素,并且可能出现的等可能结果数目较多时,为不重不漏地列出所有等可能的结果,通常采用列表法。
包括两种情况:
(1)同时进行两种相同的操作;
(2)先后进行两次相同的操作.
①列表
②通过表格确定公式中m, n的值
③利用P(A)= 计算事件的概率
????????
?
运用列表法求概率的步骤
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况
列表法中表格构造特点:
列表时,列举顺序不能颠倒.
例2 利用如图所示的两个转盘玩配紫色游戏(红色和蓝色可以配成紫色),两个转盘各转一次,则指针所指区域可以配成紫色的概率为多少?
跟踪训练
新知探究
{5940675A-B579-460E-94D1-54222C63F5DA}
红
黄
蓝
蓝
(红,蓝)
(黄,蓝)
(蓝,蓝)
黄
(红,黄)
(黄,黄)
(蓝,黄)
红
(红,红)
(黄,红)
(蓝,红)
黄
(红,黄)
(黄,黄)
(蓝,黄)
红
(红,红)
(黄,红)
(蓝,红)
由上表可知,共有15种等可能的结果,其中可以配成紫色的结果有3种,所以P(可以配成紫色) = 315=15 .
?
解:列表如下.
转盘(2) 颜色
转盘(1) 颜色
第1次
第2次
1
2
3
4
1
2
3
4
(1,3)
(1,1)
(2,1)
(3,1)
(4,1)
(1,2)
(2,2 )
(3,2)
(4,2)
(2,3 )
(3,3)
(4,3)
(1,4)
(2,4 )
(3,4)
(4,4)
2.一个不透明的袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机地摸取一个小球然后放回,再随机地摸出一个小球.求下列事件的概率:
(1)两次取出的小球标号相同;
(2)两次取出的小球标号和等于4.
解:(1)记两次取出的小球标号 相同为事件A.
?(2)记两次取出的小球标号和等于4为事件B.
????(????)=416=14
?
????(????)=316
?
1.把一副普通扑克牌中的13张黑桃牌洗匀后正面向下放在桌子上,从中随机抽取一张,求下列事件的概率:
(1) 抽出的牌是黑桃6;
(2) 抽出的牌是黑桃10;
(3) 抽出的牌带有人像;
(4) 抽出的牌上的数小于5;
(5) 抽出的牌的花色是黑桃.
113
?
113
?
313
?
413
?
1
?
随堂练习
2.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别.随机摸出一个小球后,放回并摇匀,再随机摸出一个.求下列事件的概率:
(1) 第一次摸到红球,第二次摸到绿球;
(2) 两次都摸到相同颜色的小球;
(3) 两次摸到的小球中一个绿球、一个红球.
解:所有等可能的结果为红红、红绿、绿红、绿绿,共4种情况,
第一次摸到红球,第二次摸到绿球的情况有1种,则????(第一次摸到红球,第二次摸到绿球)=14 .
两次都摸到相同颜色的小球的情况有2种,则
????(两次都摸到相同颜色的小球)= 24=12 .
(3) 两次摸到的球中一个绿球、一个红球的情况共2种,则????(两次摸到的小球中一个绿球、一个红球)= 24=12 .
?
3.五张形状、大小、背面完全相同的卡片上分别标有数-3,
-1,0,1,2,将卡片洗匀后背面朝上放在桌面上,从中任意抽
取两张,则所抽卡片上的数的积是正数的概率是多少?
-3
-1
0
1
2
-3
3
0
-3
-6
-1
3
0
-3
6
0
0
0
0
0
1
-3
-1
0
2
2
-6
-2
0
2
积
解:列表如下
“不放回”试验反映在表格上就是去掉表格中一条对角线上的所有结果
为什么对角线上的数据没列出来呢?
隐含“不放回”.
第1次
第2次
共 种结果
20
积是正数: 种
4
P(所抽卡片上的数的积是正数) =
420
?
=15
?
易错警示:混淆“放回”与“不放回”致错
本题是不放回试验,不可能抽到两张数相同的卡片,所以列表格里要排除掉两张卡片上的数相同的情况.
列举法
关键
常用
方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验.
基本步骤
① 列表;② 确定m,n的值; ③代入概率公式计算.
正确列举出所有等
可能出现的结果.
确保试验中每种结果出现的可能性大小相等.
前提条件
课堂小结
A. B. C. D.
C
对接中考
1.(2020?北京中考)不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
解:列表如下:
{5940675A-B579-460E-94D1-54222C63F5DA}
1
2
1
2
3
2
3
4
由表可知,共有4种等可能的结果,
其中两次记录的数字之和为3的有2种结果,
所以两次记录的数字之和为3的概率为
14
?
13
?
23
?
12
?
24=12
?
故选:C
2.有6张看上去无差别的卡片,上面分别写着1, 2, 3, 4, 5, 6.随机抽取1张后,放回并混在一起,再随机抽取1张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
解:由题意得两次抽取共有36种等可能出现的结果,
第二次取出的数字能够整除第一次取出的数字的结果
有14种,即有(1,1), (2,1), (2,2), (3,1), (3,3), (4,1), (4,2), (4,4),(5,1),(5,5),(6,1),(6,2),(6,3),(6,6) ,
所以所求概率为 .
1436=718
?
3.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球然后放回,再随机摸出一个小球,求下列事件的概率.
两次摸出的小球的标号相同;
(2) 两次摸出的小球标号的和等于4.
(2) 两次取出的小球标号的和等于4的情况有三种,即(3,1),(1,3),(2,2) ,所以
P(两次摸出的小球标号的和等于4)=的概率为 316 .
?
解:由题意得随机地摸出一个小球,然后放回,再随机地摸出一个小球,共有16种等可能的结果,
(1) 其中两次摸出的小球标号相同的有(1,1),(2,2),(3,3),(4,4),共4种,所以
P(两次摸出的小球标号相同)= 416=14 .
?
第2课时
25.2 用列举法求概率
九年级上册 RJ
初中数学
上节课我们学习了哪些求概率的方法?
1.直接列举法.
2.列表法.
知识回顾
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.
3.进一步学习分类思想方法,掌握有关数学技能.
学习目标
课堂导入
小红上学要经过三个十字路口,每个路口遇到红绿灯,红、黄、绿三色灯亮的的可能性都相等,小红希望上学时经过的每个路口都是绿灯,此事件发生的概率是多少?
这个问题能用直接列表法和列表法解决吗?有什么简单的解决办法吗?
第2路口
第1路口
红
绿
黄
红
绿
黄
第3路口
一共有27种情况,每种情况发生的可能性相等,
其中三个路口都为绿灯的情况只有 种,
所以3个路口都为绿灯的概率为
127
?
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
绿
黄
红
红
红
红
红
黄
红
红
绿
黄
红
绿
红
绿
绿
红
绿
红
绿
黄
红
绿
黄
黄
绿
黄
绿
黄
红
黄
黄
红
红
红
黄
红
红
黄
黄
红
黄
绿
红
绿
黄
绿
绿
红
绿
绿
黄
绿
绿
绿
绿
黄
红
绿
黄
黄
绿
黄
绿
黄
绿
红
黄
绿
黄
黄
绿
绿
黄
黄
红
黄
黄
黄
黄
黄
绿
解:根据题意画树状图如下:
1
以上用树状图的形式反映事件发生的各种结果出现的次数和方式,以及某一事件发生的可能的次数和方式,并求出概率的方法叫做画树状图法.
画树状图法求概率的适用条件是什么呢?
当一次试验涉及两个或更多个因素时,为了不重不漏地列出所有等可能的结果,通常采用画树状图法.
知识点
新知探究
数出所有事件出现的结果数n和A事件出现的结果数m.
代入公式P(A)= 计算概率
用树状图法求概率的“四个步骤”
????????
?
①定
②画
③数
④算
确定该试验的几个步骤、顺序、每一步可能产生的结果.
列举每一步可能出现的结果,得到树状图.
例1 甲口袋中有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1) 取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2) 取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
跟踪训练
新知探究
甲
乙
丙
A
B
C
E
D
C
E
D
H I
H I
H I
H I
H I
H I
解:根据题意,可以画出如下的树状图:
A
C
H
A
C
I
A
E
I
B
C
H
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
A
D
H
A
D
I
A
E
H
由树状图可以看出,所有可能出现的结果共有12种,
即ACH,ACI,ADH,ADI,AEH,AEI,BCH,BCI,BDH,BDI,BEH, BEI,
这些结果出现的可能性相等.
(2)全是辅音字母的结果共有 种,
全部为元音字母的结果只有 种,
(1)只有1个元音字母的结果有 种,
所以P(1个元音)= 512 .
?
有2个元音字母的结果有 种,
所以P(2个元音)= 412=13 .
?
所以P(3个元音)= 112 .
?
所以P(3个辅音)= 212=16.
?
5
1
4
2
用列举法求事件的概率的方法:
直接列举法;
列表法;
画树状图法.
注意:用列举法求概率时,各种结果出现的可能性必须相同,并要不重不漏地列举出所有等可能的结果.
什么时候该用列表法什么时候该用画树状图法呢?
当试验包含两步时,既可以用列表法有又可以用画树状图法;当试验包含三步或三步以上时,不能用列表法,用画树状图法比较方便.
例2 现有A,B,C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包、一个糖包和一个韭菜包, C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那么老师选的包子全部是酸菜包的概率是多少?
解:根据题意,画出树状图如下
由树状图得,所有等可能出现的结果有 ,
P(老师选的包子全部是酸菜包)= 218=19 .
?
A盘
B盘
C盘
酸
糖
韭
酸
酸
糖
酸
酸
酸
酸
糖
韭
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
酸
糖
糖
韭
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
韭
酸
糖
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
韭
酸
糖
糖
酸
酸
糖
酸
糖
糖
糖
酸
糖
糖
糖
韭
糖
糖
酸
酸
酸
2种
所以
选的包子全部是酸菜包的结果有 ,
18种
1.如图(1)是一电路AB的开关控制,任意闭合两个开关,可能会使电路形成通路.
(1) 补全如图(2)所示的树状图;
(2) 求使电路形成通路的概率.
随堂练习
分析:此电路形成通路的条件是开关a,b闭合其中的一个,开关c,d,e闭合其中的一个,因此,当同时闭合的两个开关中一个是a或b,另一个是c或d或e时,电路才形成通路。
解:(1) 补全树状图如图所示.
所以P(电路形成通路)= .
a
不通
通
通
通
b
不通
通
通
通
c
通
通
不通
不通
e
通
通
不通
不通
d
通
通
不通
不通
c
b
d
e
b
a
c
e
b
a
d
e
c
a
d
e
b
a
c
d
1220=35
?
(2)由树状图可知,所有等可能出现的结果有 种,
其中能使电路形成通路的结果有 种,
12
20
2.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1) 三辆车全部继续直行;
(2) 两车向右,一车向左;
(3) 至少两车向左.
分析:包括两车向左、三车向左,其中两车向左又可分为两车向左一车向右、两车向左一车直行两种情况.
第一辆
左
右
第二辆
第三辆
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
(1) P(全部继续直行) = 127 ;
?
(2) P(两车向右,一车向左) = 327=19 ;
?
(3) P(至少两车向左) = 727 .
?
左
右
直
左
右
直
左直右
左直右
左直右
解:根据题意,画树状图如下:
左
直
直
左
左
左
直
左
左
右
左
直
左
左
左
左
直
右
左
右
左
左
右
右
左
右
直
直
左
左
直
直
左
直
直
直
直
直
右
直
右
直
左
直
左
直
右
直
直
右
右
右
左
左
直
左
右
右
左
右
右
直
左
右
直
直
右
直
左
右
右
左
右
右
直
右
右
右
右
右
直
树状图
步骤
适用条件
试验涉及两个或更多个因素时用此方法.
注意
①弄清试验涉及的因素个数或试验步骤分几步;
③利用概率公式进行计算.
①确定试验的步骤、每一步产生的结果;
②在树状图下面写出所有等可能的结果;
②在摸球试验中一定要弄清“放回”还是“不放回”.
课堂小结
③数出所有事件出现的结果数n和A事件出现的结果数m.
对接中考
1.(2020?玉林中考)经过人民中路十字路口红绿灯处的两辆汽车,可能直行,也可能向左转,如果这两种可能性大小相同,则至少有一辆向左转的概率是 .
解析:画树状图如下:
由树状图知,共有4种等可能的结果,
34
?
第一辆
直行
左转
直行
左转
直行
左转
第二辆
34
?
所以至少有一辆向左转的概为 .
其中至少有一辆向左转的结果有3种,
2.小颖和小明用如图所示的两个转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可配成紫色,此时小颖得2分,否则小明得1分,这个游戏公平吗?若你认为不公平,如何修改规则才能使游戏对双方公平?
解:画出树状图如图所示:
游戏规则可改为:若配成紫色,则小颖得2分;若两次转到相同颜色,则小明得2分;配成其他颜色两人均不得分.(修改方式不唯一)
红
黄
黄
红
红
黄
黄
蓝
A转盘
B转盘
由树状图可知,一共有6种等可能的结果,
其中能配成紫色的有1种,
所以能配成紫色的概率是 16 ,
?
不能配成紫色的概率是 56.
?
因为 16×2 < 56 ,
?
所以这个游戏不公平.
技巧点拨:保证游戏规则公平的两种途径①使用参与游戏各方获胜的概率相同;②参与游戏的各方获胜的概率不同时,可以通过控制分值使各方获胜概率与分值的乘积相等.
易错警示:本题易因忽略等可能性出错.B转盘虽然只有两种颜色,但因为红色和黄色所占的比例不一样,所以要使可能性相同,黄色应分成两份.
3.(2020.南州)某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是 .
解:画出树状图得,
其中出场顺序恰好是甲、
乙、丙的只有1种结果,
甲
丙
乙
丙
乙
丙
甲
乙
甲
丙
乙
甲
丙
甲
乙
16
?
16
?
第1个
第2个
第3个
共有6种等可能的结果,
∴出场顺序恰好是甲、乙、丙的概率为 .
同课章节目录
