2021-2022学年人教版数学七年级上册2.2 整式的加减(第1课时)课件(41张ppt)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册2.2 整式的加减(第1课时)课件(41张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 419.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 16:56:23 | ||
图片预览











文档简介
2.2 整式的加减
人教版· 数学· 七年级(上)
第二章 整式的加减
第1课时 合并同类项
1.知道同类项的概念,会识别同类项。(难点)
2.掌握合并同类项的法则,并能准确合并同类项。(重点)
3.能在合并同类项的基础上进行化简、求值运算。
学习目标
如果有一罐硬币(分别为一角、五角、一元),你会如何去数呢?
导入新知
① 8n,5n;
②3ab2,-ab2;
③6xy,-3xy;
④-7a2b,2a2b.
观察下列各组单项式有什么特点?
1.所含字母相同.
2.相同字母的指数也相同.
新知一 同类项
合作探究
注意:(1)是不是同类项有“两个无关”: ①与系数无关;
②与字母的排列顺序无关,如3mn与-nm是同类项.
(2)同类项都是单项式.
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
几个常数项也是同类项.
抓住“两个相同”:
一是所含的字母要完全相同,
二是相同字母的指数要相同,
这两个条件缺一不可.
同类项的判别方法:
下列各组单项式:①y与y2 ;②-a2b3与2a2b3 ;③2x2y与5yx2;④-2 019与0.其中是同类项的有( )
A.4组 B.3组 C.2组 D.1组
B
跟踪训练
新知探究
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明应该怎么说?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
面包
苹果
草莓
饮料
爸爸
2
1
2
1
妈妈
1
1
3
1
小明
1
1
3
1
新知二 合并同类项
____个面包____个苹果____个草莓_____瓶饮料
4
2个面包+1个面包+1个面包= 个面包
2个草莓+3个草莓+3个草莓= 个草莓
4
8
3
8
3
1个苹果+1个苹果+1个苹果= 个苹果
3
1瓶饮料+1瓶饮料+1瓶饮料= 瓶饮料
3
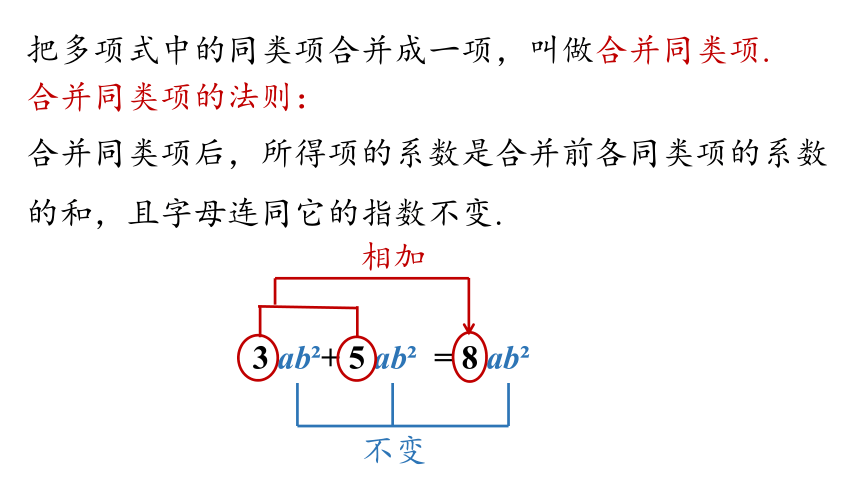
合并同类项的法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
把多项式中的同类项合并成一项,叫做合并同类项.
3 ab?+ 5 ab? = 8 ab?
相加
不变
合并同类项的一般步骤:
一找:找出同类项,当项数较多时,通常在同类项的下面做相同的标记;
二移:运用加法交换律、结合律将多项式中的同类项结合;
三合:利用合并同类项法则,合并同类项;
四排:合并后的结果按某一个字母的降幂(或升幂)排列.
注意:1.合并同类项时,只能把同类项合并成一项,不是同类项的不能合并,不能合并的项,在每一步运算中都要写出,不能漏掉.
2.所有的常数项都是同类项,合并时把它们结合在一起,运用有理数的运算法则进行合并.
3.若两个同类项的系数互为相反数,则合并这两个同类项的结果为0.
例1 合并下列各式的同类项:
(1)xy2-15xy2;(2)-3x2y+2x2y+3xy2 - 2xy2;
(3)4a2 + 3b2 +2ab-4a2 -4b2.
?
解:(1) xy2-15xy2 = (1- 15?)xy2 = 45xy2.
?
(2) -3x2y+2x2y+3xy2 - 2xy2
=(-3+2) x2y+(3-2) xy2
= -x2y+xy2.
(3) 4a2 + 3b2 +2ab-4a2 -4b2
= (4a2-4a2) + ( 3b2 -4b2) + 2ab
= (4-4)a2 + (3-4)b2 + 2ab
=-b2 + 2ab.
合并同类项时要注意“一相加,两不变”,“一相加”是指各同类项的系数相加;“两不变”是指字母连同它的指数不变.
例2 (1)求多项式 2x2-5x+x2+4x-3x2 -2 的值,其中x=?12;
(2)求多项式 3a+abc-13c2-3a+ 13c2 的值,其中 a=-16,b=2,c=-3.
?
分析:在求多项式的值时,可以先将多项式中的同类项合并,然后再求值,这样做往往可以简化计算.
解:(1) 2x2-5x+x2+4x-3x2 -2
= (2+1-3) x2 + (-5+4) x-2
= -x-2.
例2 (1)求多项式 2x2-5x+x2+4x-3x2 -2 的值,其中x=?12;
?
当 x = 12时,原式= ?12 - 2= - 52.
?
解: 3a+abc - 13c2 - 3a + 13c2
= (3-3) a +abc+ ( - 13?+ 13?) c2
= abc
?
例2 (2)求多项式 3a+abc - 13c2 - 3a + 13c2 的值,其中 a=-?16,b=2,c= -3.
?
当a= -16,b=2,c= -3时,原式= -16×2×(-3)=1.
?
计算:xy2-5y3-2xy2+5y3.
解:xy2-5y3-2xy2+5y3
=(xy2 -2xy2)+(-5y3 +5y3)
=(1-2)xy2 +(-5+5)y3
=-xy2.
巩固新知
1.计算3x2-x2的结果是( )
A.2 B.2x2 C.2x D.4x2
B
合并同类项时,只需要系数相加,其他都不用变
课堂练习
2.若单项式 2x2ym 与-13xny4可以合并成一项,则 nm = .
?
16
解析:根据题意,得 2x2ym 与-13xny4是同类项,
所以n=2,m=4,所以nm=24=16.
?
两个单项式能合并,说明这两个单项式是同类项.
3.水库中水位第一天连续下降了a小时,平均每小时下降2 cm;第二天连续上升了a小时,平均每小时上升
0.5 cm,这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正. 第一天水位的变化量是-2a cm,第二天水位的变化量是0.5a cm.
两天水位的总变化量是-2a+0.5a=(-2+0.5)a=-1.5a(cm).
所以这两天水位总的变化情况为下降了1.5a cm.
同 类 项
合并同类项
法则
(1)字母相同;
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三合、四排
(一相加两不变)
两无关
两相同
(2)相同字母的指数相同.
归纳新知
1.下列各式中,与-ab2是同类项的是( )
A.-3ab2 B.4a2b
C.3ab D.2a2b2
A
课后练习
A
B
4.写出单项式-3xy2的一个同类项:__________________.
xy2 (答案不唯一)
5.(2019·台州)计算2a-3a,结果正确的是( )
A.-1 B.1 C.-a D.A
6.下列合并同类项正确的是( )
A.5x2y-4x2y=x2y B.5x+2y=7xy
C.5x3-3x3=2 D.2x+4x=8x2
C
A
7.式子4x2+2y-3xy+7+3y-8x2-2合并同类项的结果有( )
A.一项 B.二项 C.三项 D.四项
8.(2019·怀化)合并同类项:4a2+6a2-a2=________.
9.把(a-b)看作一个整体,合并同类项:3(a-b)+4(a-b)-2(a-b)=_________.
D
9a2
5(a-b)
10.合并下列各式的同类项:
(1)5m+2n-m-3n;
(2)3a2-1-2a-5+3a-a2;
(3)-5m2n+4mn2-2mn+6m2n+3mn.
解:原式=(5-1)m+(2-3)n=4m-n.
解:原式=(3-1)a2+(-2+3)a+(-1-5)=2a2+a-6.
解:原式=(-5+6)m2n+4mn2+(-2+3)mn=m2n+4mn2+mn.
13.有三个连续偶数,若中间一个偶数为2n,则另两个偶数为
___________________,这三个连续偶数的和为________.
2n-2,2n+2
6n
14.三峡水库的水位第一天连续下降a小时,每小时平均下降3 cm,第二天连续上升2小时,每小时平均上升a cm,第三天水位又下降a cm,则这三天三峡水库的水位总的变化情况是__________.
下降2a cm
15.下列化简:①5xy-x=5y;②5ab-5ba=0;③2a2+3a2=5a4;④-5m2n+8nm2=3m2n.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
16.已知2amb+4a2bn=6a2b,则-2m+n的值为( )
A.-1 B.2 C.-3 D.4
17.若关于x的多项式3x3+k2x2-4x2+x-5中不含x2项,则k的值为( )
A.0 B.2 C.-2 D.2或-2
B
C
D
18.式子m-3m+5m-7m+…-2 019m合并同类项的结果为( )
A.0 B.-1 010m C.m D.1 010m
19.若xy<0,y>0,则化简5|x|+3x= ________.
20.已知多项式4x2-3mx+2+m的值与m的大小无关,则x的值为 .
B
-2x
21.先化简,再求值:
(1)3x-4x3+7-3x+2x3+1,其中x=-2;
解:原式=-2x3+8.当x=-2时,原式=-2×(-2)3+8=24.
22.某学校组织七、八年级全体学生参观革命老区西柏坡,七年级租用45座大巴车x辆,60座大巴车y辆,八年级租用60座大巴车x辆,30座中巴车y辆,每辆车恰好坐满.
(1)用含x,y的式子表示该学校七、八年级的总人数;
(2)当x=4,y=7时,该学校七、八年级共有多少学生?
解:(1)七、八年级的总人数为:45x+60y+60x+30y=105x+90y.
(2)当x=4,y=7时,105x+90y=105×4+90×7=1 050.所以该学校七、八年级共有1 050名学生.
23.有这样一道题:“当a=999,b=9 999时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”小明说:本题中a,b的值这么大,怎么好算呢?小强说:本题中a=999,b=9 999是多余的条件.小红马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意谁的观点?请说明理由.
解:我同意小强的观点.理由:因为7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3=(7+3-10)a3+(-6+6)a3b+(3-3)a2b=0.即化简后多项式的值与a,b无关,所以a=999,b=9 999是多余的条件,故小强的观点正确.
再
见
人教版· 数学· 七年级(上)
第二章 整式的加减
第1课时 合并同类项
1.知道同类项的概念,会识别同类项。(难点)
2.掌握合并同类项的法则,并能准确合并同类项。(重点)
3.能在合并同类项的基础上进行化简、求值运算。
学习目标
如果有一罐硬币(分别为一角、五角、一元),你会如何去数呢?
导入新知
① 8n,5n;
②3ab2,-ab2;
③6xy,-3xy;
④-7a2b,2a2b.
观察下列各组单项式有什么特点?
1.所含字母相同.
2.相同字母的指数也相同.
新知一 同类项
合作探究
注意:(1)是不是同类项有“两个无关”: ①与系数无关;
②与字母的排列顺序无关,如3mn与-nm是同类项.
(2)同类项都是单项式.
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
几个常数项也是同类项.
抓住“两个相同”:
一是所含的字母要完全相同,
二是相同字母的指数要相同,
这两个条件缺一不可.
同类项的判别方法:
下列各组单项式:①y与y2 ;②-a2b3与2a2b3 ;③2x2y与5yx2;④-2 019与0.其中是同类项的有( )
A.4组 B.3组 C.2组 D.1组
B
跟踪训练
新知探究
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明应该怎么说?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
面包
苹果
草莓
饮料
爸爸
2
1
2
1
妈妈
1
1
3
1
小明
1
1
3
1
新知二 合并同类项
____个面包____个苹果____个草莓_____瓶饮料
4
2个面包+1个面包+1个面包= 个面包
2个草莓+3个草莓+3个草莓= 个草莓
4
8
3
8
3
1个苹果+1个苹果+1个苹果= 个苹果
3
1瓶饮料+1瓶饮料+1瓶饮料= 瓶饮料
3
合并同类项的法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
把多项式中的同类项合并成一项,叫做合并同类项.
3 ab?+ 5 ab? = 8 ab?
相加
不变
合并同类项的一般步骤:
一找:找出同类项,当项数较多时,通常在同类项的下面做相同的标记;
二移:运用加法交换律、结合律将多项式中的同类项结合;
三合:利用合并同类项法则,合并同类项;
四排:合并后的结果按某一个字母的降幂(或升幂)排列.
注意:1.合并同类项时,只能把同类项合并成一项,不是同类项的不能合并,不能合并的项,在每一步运算中都要写出,不能漏掉.
2.所有的常数项都是同类项,合并时把它们结合在一起,运用有理数的运算法则进行合并.
3.若两个同类项的系数互为相反数,则合并这两个同类项的结果为0.
例1 合并下列各式的同类项:
(1)xy2-15xy2;(2)-3x2y+2x2y+3xy2 - 2xy2;
(3)4a2 + 3b2 +2ab-4a2 -4b2.
?
解:(1) xy2-15xy2 = (1- 15?)xy2 = 45xy2.
?
(2) -3x2y+2x2y+3xy2 - 2xy2
=(-3+2) x2y+(3-2) xy2
= -x2y+xy2.
(3) 4a2 + 3b2 +2ab-4a2 -4b2
= (4a2-4a2) + ( 3b2 -4b2) + 2ab
= (4-4)a2 + (3-4)b2 + 2ab
=-b2 + 2ab.
合并同类项时要注意“一相加,两不变”,“一相加”是指各同类项的系数相加;“两不变”是指字母连同它的指数不变.
例2 (1)求多项式 2x2-5x+x2+4x-3x2 -2 的值,其中x=?12;
(2)求多项式 3a+abc-13c2-3a+ 13c2 的值,其中 a=-16,b=2,c=-3.
?
分析:在求多项式的值时,可以先将多项式中的同类项合并,然后再求值,这样做往往可以简化计算.
解:(1) 2x2-5x+x2+4x-3x2 -2
= (2+1-3) x2 + (-5+4) x-2
= -x-2.
例2 (1)求多项式 2x2-5x+x2+4x-3x2 -2 的值,其中x=?12;
?
当 x = 12时,原式= ?12 - 2= - 52.
?
解: 3a+abc - 13c2 - 3a + 13c2
= (3-3) a +abc+ ( - 13?+ 13?) c2
= abc
?
例2 (2)求多项式 3a+abc - 13c2 - 3a + 13c2 的值,其中 a=-?16,b=2,c= -3.
?
当a= -16,b=2,c= -3时,原式= -16×2×(-3)=1.
?
计算:xy2-5y3-2xy2+5y3.
解:xy2-5y3-2xy2+5y3
=(xy2 -2xy2)+(-5y3 +5y3)
=(1-2)xy2 +(-5+5)y3
=-xy2.
巩固新知
1.计算3x2-x2的结果是( )
A.2 B.2x2 C.2x D.4x2
B
合并同类项时,只需要系数相加,其他都不用变
课堂练习
2.若单项式 2x2ym 与-13xny4可以合并成一项,则 nm = .
?
16
解析:根据题意,得 2x2ym 与-13xny4是同类项,
所以n=2,m=4,所以nm=24=16.
?
两个单项式能合并,说明这两个单项式是同类项.
3.水库中水位第一天连续下降了a小时,平均每小时下降2 cm;第二天连续上升了a小时,平均每小时上升
0.5 cm,这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正. 第一天水位的变化量是-2a cm,第二天水位的变化量是0.5a cm.
两天水位的总变化量是-2a+0.5a=(-2+0.5)a=-1.5a(cm).
所以这两天水位总的变化情况为下降了1.5a cm.
同 类 项
合并同类项
法则
(1)字母相同;
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三合、四排
(一相加两不变)
两无关
两相同
(2)相同字母的指数相同.
归纳新知
1.下列各式中,与-ab2是同类项的是( )
A.-3ab2 B.4a2b
C.3ab D.2a2b2
A
课后练习
A
B
4.写出单项式-3xy2的一个同类项:__________________.
xy2 (答案不唯一)
5.(2019·台州)计算2a-3a,结果正确的是( )
A.-1 B.1 C.-a D.A
6.下列合并同类项正确的是( )
A.5x2y-4x2y=x2y B.5x+2y=7xy
C.5x3-3x3=2 D.2x+4x=8x2
C
A
7.式子4x2+2y-3xy+7+3y-8x2-2合并同类项的结果有( )
A.一项 B.二项 C.三项 D.四项
8.(2019·怀化)合并同类项:4a2+6a2-a2=________.
9.把(a-b)看作一个整体,合并同类项:3(a-b)+4(a-b)-2(a-b)=_________.
D
9a2
5(a-b)
10.合并下列各式的同类项:
(1)5m+2n-m-3n;
(2)3a2-1-2a-5+3a-a2;
(3)-5m2n+4mn2-2mn+6m2n+3mn.
解:原式=(5-1)m+(2-3)n=4m-n.
解:原式=(3-1)a2+(-2+3)a+(-1-5)=2a2+a-6.
解:原式=(-5+6)m2n+4mn2+(-2+3)mn=m2n+4mn2+mn.
13.有三个连续偶数,若中间一个偶数为2n,则另两个偶数为
___________________,这三个连续偶数的和为________.
2n-2,2n+2
6n
14.三峡水库的水位第一天连续下降a小时,每小时平均下降3 cm,第二天连续上升2小时,每小时平均上升a cm,第三天水位又下降a cm,则这三天三峡水库的水位总的变化情况是__________.
下降2a cm
15.下列化简:①5xy-x=5y;②5ab-5ba=0;③2a2+3a2=5a4;④-5m2n+8nm2=3m2n.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
16.已知2amb+4a2bn=6a2b,则-2m+n的值为( )
A.-1 B.2 C.-3 D.4
17.若关于x的多项式3x3+k2x2-4x2+x-5中不含x2项,则k的值为( )
A.0 B.2 C.-2 D.2或-2
B
C
D
18.式子m-3m+5m-7m+…-2 019m合并同类项的结果为( )
A.0 B.-1 010m C.m D.1 010m
19.若xy<0,y>0,则化简5|x|+3x= ________.
20.已知多项式4x2-3mx+2+m的值与m的大小无关,则x的值为 .
B
-2x
21.先化简,再求值:
(1)3x-4x3+7-3x+2x3+1,其中x=-2;
解:原式=-2x3+8.当x=-2时,原式=-2×(-2)3+8=24.
22.某学校组织七、八年级全体学生参观革命老区西柏坡,七年级租用45座大巴车x辆,60座大巴车y辆,八年级租用60座大巴车x辆,30座中巴车y辆,每辆车恰好坐满.
(1)用含x,y的式子表示该学校七、八年级的总人数;
(2)当x=4,y=7时,该学校七、八年级共有多少学生?
解:(1)七、八年级的总人数为:45x+60y+60x+30y=105x+90y.
(2)当x=4,y=7时,105x+90y=105×4+90×7=1 050.所以该学校七、八年级共有1 050名学生.
23.有这样一道题:“当a=999,b=9 999时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”小明说:本题中a,b的值这么大,怎么好算呢?小强说:本题中a=999,b=9 999是多余的条件.小红马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意谁的观点?请说明理由.
解:我同意小强的观点.理由:因为7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3=(7+3-10)a3+(-6+6)a3b+(3-3)a2b=0.即化简后多项式的值与a,b无关,所以a=999,b=9 999是多余的条件,故小强的观点正确.
再
见
同课章节目录
