【数学】1-4《生活中的优化问题》课件(人教A版选修2-2)
文档属性
| 名称 | 【数学】1-4《生活中的优化问题》课件(人教A版选修2-2) |  | |
| 格式 | zip | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-11 16:40:25 | ||
图片预览


文档简介
(共8张PPT)
2、求最大(最小)值应用题的一般方法:
(1)分析实际问题中各量之间的关系,把实际问题化为数学问题,建立函数关系式,这是关键一步;
(2)确定函数定义域,并求出极值点;
(3)比较各极值与定义域端点函数的大小, 结合实际,确定最值或最值点.
1、实际应用问题的表现形式,常常不是以纯数学模式反映出来:
首先,通过审题,认识问题的背景,抽象出问题的实质;
其次,建立相应的数学模型, 将应用问题转化为数学问题,再解.
3.4生活中的优化问题
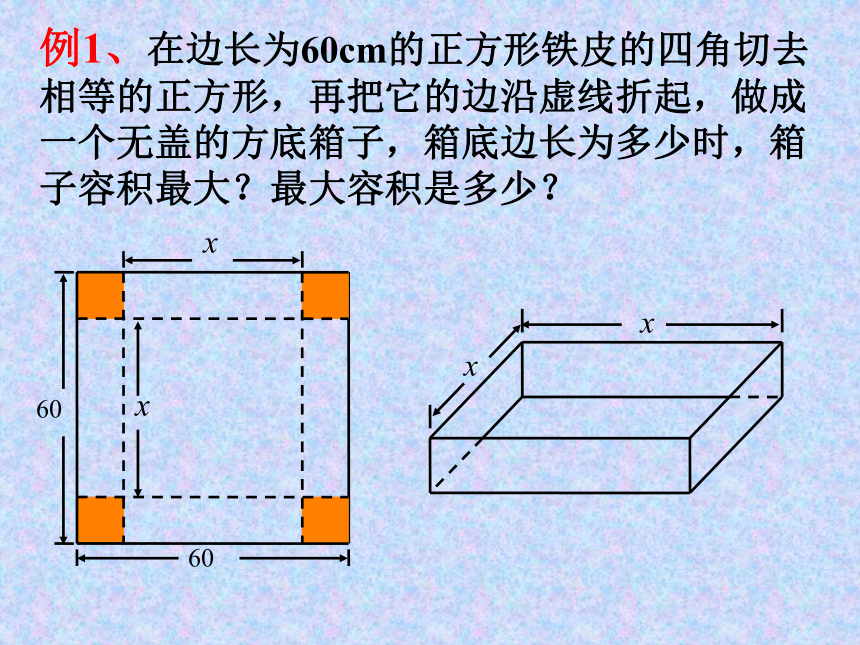
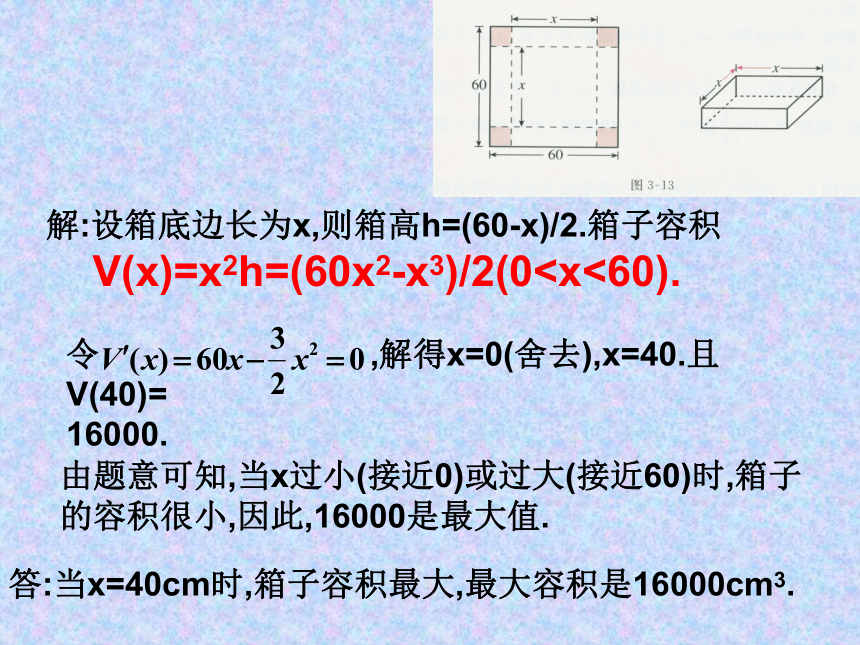
例1、在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(0令 ,解得x=0(舍去),x=40.且V(40)=
16000.
由题意可知,当x过小(接近0)或过大(接近60)时,箱子的容积很小,因此,16000是最大值.
答:当x=40cm时,箱子容积最大,最大容积是16000cm3.
2、若函数 f ( x )在定义域内只有一个极值点x0 ,则不需与端点比较, f ( x0 )即是所求的最大值或最小值.
说明
1、设出变量找出函数关系式;
(所说区间的也适用于开区间或无穷区间)
确定出定义域;
所得结果符合问题的实际意义
h
r
例2、要生产一批带盖的圆柱形铁桶,要求每个铁桶的容积为定值V,怎样设计桶的底面半径才能使材料最省?此时高与底面半径比为多少?
解:设圆柱的高为h,底半径为r,则表面积S=2πrh+2πr2.
由V=πr2h,得 ,则
令 ,解得 ,从而
,即h=2r.
由于S(r)只有一个极值,所以它是最小值.
答:当罐的高与底直径相等时,所用的材料最省.
x
y
例3: 如图,在二次函数f(x)=
4x-x2的图象与x轴所
围成的图形中有一个
内接矩形ABCD,求这
个矩形的最大面积.
解:设B(x,0)(0A(x, 4x-x2).
从而|AB|= 4x-x2,|BC|=2(2-x).故矩形ABCD的面积
为:S(x)=|AB||BC|=2x3-12x2+16x(0令 ,得
所以当 时,
因此当点B为 时,矩形的最大面积是
应用问题要引起重视.
(1)利用函数的导数求函数的最值在求函数的值域、
不等式的证明及解法中有广泛的作用。
(2)在实际问题中如果可以判定可导函数在定义域内
存在最大(小)值,而且函数在这个定义域内又只有
唯一的极值点,那么立即可以判定,这个极值点的函
数值就是最大(小)值,这一点在解决实际问题时很
有用.
课堂小结
2、求最大(最小)值应用题的一般方法:
(1)分析实际问题中各量之间的关系,把实际问题化为数学问题,建立函数关系式,这是关键一步;
(2)确定函数定义域,并求出极值点;
(3)比较各极值与定义域端点函数的大小, 结合实际,确定最值或最值点.
1、实际应用问题的表现形式,常常不是以纯数学模式反映出来:
首先,通过审题,认识问题的背景,抽象出问题的实质;
其次,建立相应的数学模型, 将应用问题转化为数学问题,再解.
3.4生活中的优化问题
例1、在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(0
16000.
由题意可知,当x过小(接近0)或过大(接近60)时,箱子的容积很小,因此,16000是最大值.
答:当x=40cm时,箱子容积最大,最大容积是16000cm3.
2、若函数 f ( x )在定义域内只有一个极值点x0 ,则不需与端点比较, f ( x0 )即是所求的最大值或最小值.
说明
1、设出变量找出函数关系式;
(所说区间的也适用于开区间或无穷区间)
确定出定义域;
所得结果符合问题的实际意义
h
r
例2、要生产一批带盖的圆柱形铁桶,要求每个铁桶的容积为定值V,怎样设计桶的底面半径才能使材料最省?此时高与底面半径比为多少?
解:设圆柱的高为h,底半径为r,则表面积S=2πrh+2πr2.
由V=πr2h,得 ,则
令 ,解得 ,从而
,即h=2r.
由于S(r)只有一个极值,所以它是最小值.
答:当罐的高与底直径相等时,所用的材料最省.
x
y
例3: 如图,在二次函数f(x)=
4x-x2的图象与x轴所
围成的图形中有一个
内接矩形ABCD,求这
个矩形的最大面积.
解:设B(x,0)(0
从而|AB|= 4x-x2,|BC|=2(2-x).故矩形ABCD的面积
为:S(x)=|AB||BC|=2x3-12x2+16x(0
所以当 时,
因此当点B为 时,矩形的最大面积是
应用问题要引起重视.
(1)利用函数的导数求函数的最值在求函数的值域、
不等式的证明及解法中有广泛的作用。
(2)在实际问题中如果可以判定可导函数在定义域内
存在最大(小)值,而且函数在这个定义域内又只有
唯一的极值点,那么立即可以判定,这个极值点的函
数值就是最大(小)值,这一点在解决实际问题时很
有用.
课堂小结
