【数学】1-5-1《曲边梯形的面积》课件(新人教A版选修2-2)
文档属性
| 名称 | 【数学】1-5-1《曲边梯形的面积》课件(新人教A版选修2-2) |

|
|
| 格式 | zip | ||
| 文件大小 | 472.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-11 16:40:25 | ||
图片预览



文档简介
(共13张PPT)
我们已经学会了正方形,三角形,梯形等面积的计算。
情景设计:
面积
但我们生活与工程实际中经常接触的大都是曲边图形,他们的面积怎么计算呢?
这些图形有一个共同的特征:
每条边都是直的线段。
课题:曲边梯形的面积
我行 我能 我要成功 我能成功
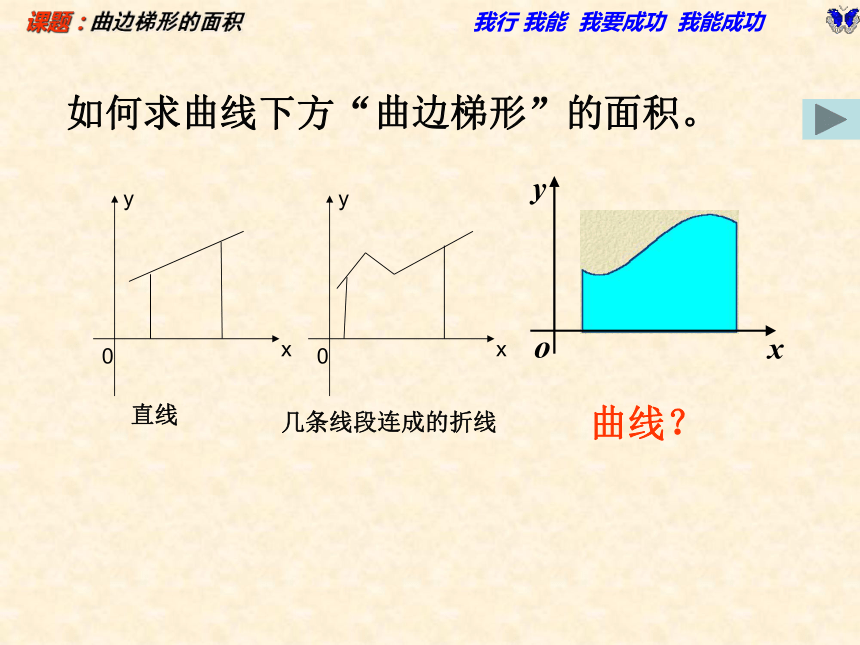
如何求曲线下方“曲边梯形”的面积。
x
y
0
x
y
0
x
y
o
直线
几条线段连成的折线
曲线?
课题:曲边梯形的面积
我行 我能 我要成功 我能成功
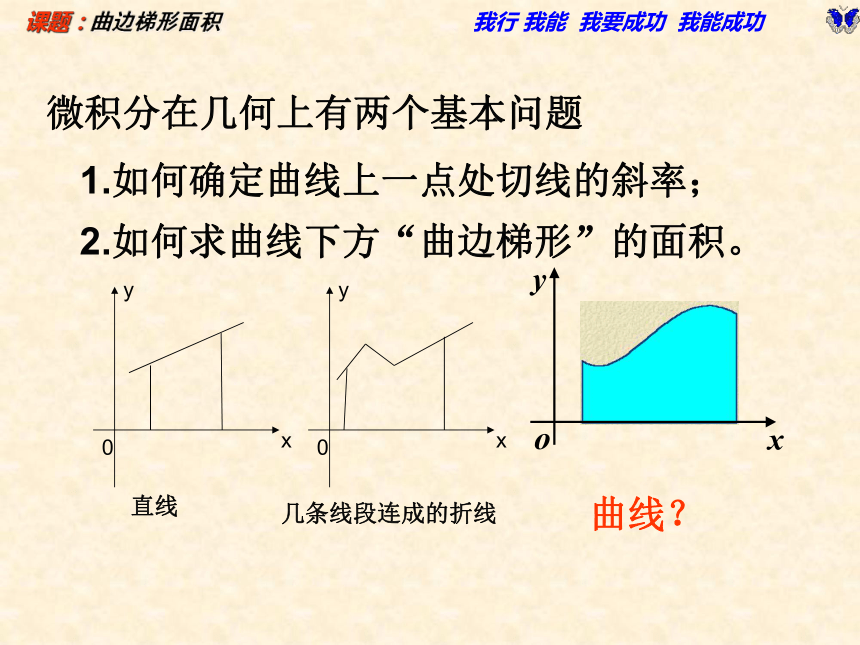
微积分在几何上有两个基本问题
1.如何确定曲线上一点处切线的斜率;
2.如何求曲线下方“曲边梯形”的面积。
x
y
0
x
y
0
x
y
o
直线
几条线段连成的折线
曲线?
课题:曲边梯形面积
我行 我能 我要成功 我能成功
曲边梯形的面积
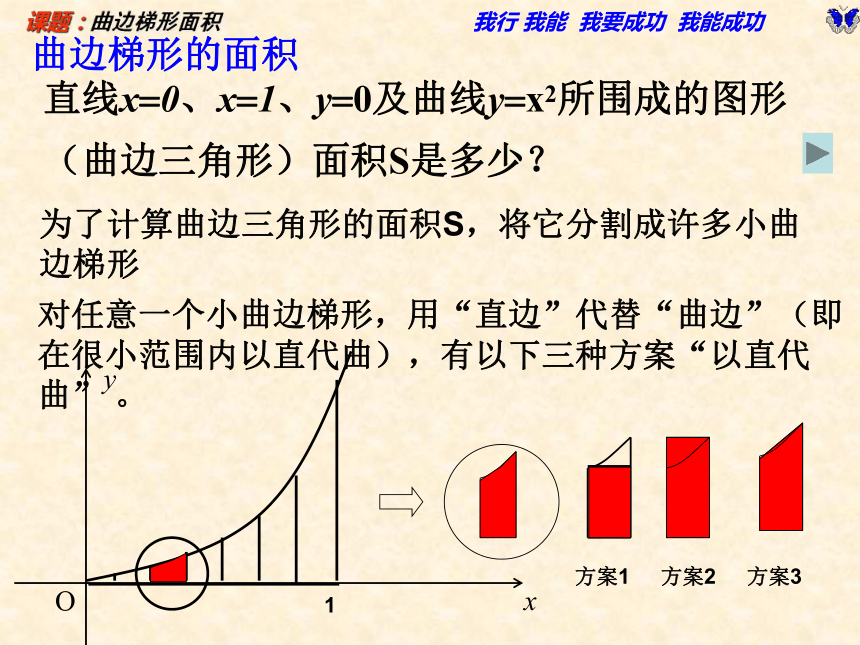
直线x 0、x 1、y 0及曲线y x2所围成的图形(曲边三角形)面积S是多少?
x
y
O
1
方案1
方案2
方案3
为了计算曲边三角形的面积S,将它分割成许多小曲边梯形
对任意一个小曲边梯形,用“直边”代替“曲边”(即在很小范围内以直代曲),有以下三种方案“以直代曲” 。
课题:曲边梯形面积
我行 我能 我要成功 我能成功
y = f(x)
b
a
x
y
O
S S1+ S2 + + Sn
将曲边梯形分成 n个小曲边梯形,并用小矩阵形的面积代替小曲边梯形的面积, 于是曲边梯形的面积S近似为
S1
Si
Sn
课题:曲边梯形面积
我行 我能 我要成功 我能成功
分割越细,面积的近似值就越精确。当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S。
下面用第一种方案“以直代曲”的具体操作过程
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(1)分割
把区间[0,1]等分成n个小区间:
过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(2) 以直代曲
(3)作和
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(4)逼近
分割
以直代曲
作和
逼近
课题:曲边梯形面积
我行 我能 我要成功 我能成功
当分点非常多(n非常大)时,可以认为f(x)在小区间上几乎没有变化(或变化非常小),从而可以取小区间内任意一点xi对应的函数值f(xi)作为小矩形一边的长,于是f(xi) △x来近似表示小曲边梯形的面积
表示了曲边梯形面积的近似值
课题:曲边梯形面积
我行 我能 我要成功 我能成功
例1:火箭发射后ts的速度为v(t)(单位:m/s),假定0≤t≤10,对函数v(t)按上式所作的和具有怎样的实际意义?
例2:如图,有两个点电荷A、B,电量分别为qA,qB,,固定电荷A,将电荷B从距A为a处移到距A为b 处,求库仑力对电荷B所做的功。
课题:曲边梯形面积
我行 我能 我要成功 我能成功
我们已经学会了正方形,三角形,梯形等面积的计算。
情景设计:
面积
但我们生活与工程实际中经常接触的大都是曲边图形,他们的面积怎么计算呢?
这些图形有一个共同的特征:
每条边都是直的线段。
课题:曲边梯形的面积
我行 我能 我要成功 我能成功
如何求曲线下方“曲边梯形”的面积。
x
y
0
x
y
0
x
y
o
直线
几条线段连成的折线
曲线?
课题:曲边梯形的面积
我行 我能 我要成功 我能成功
微积分在几何上有两个基本问题
1.如何确定曲线上一点处切线的斜率;
2.如何求曲线下方“曲边梯形”的面积。
x
y
0
x
y
0
x
y
o
直线
几条线段连成的折线
曲线?
课题:曲边梯形面积
我行 我能 我要成功 我能成功
曲边梯形的面积
直线x 0、x 1、y 0及曲线y x2所围成的图形(曲边三角形)面积S是多少?
x
y
O
1
方案1
方案2
方案3
为了计算曲边三角形的面积S,将它分割成许多小曲边梯形
对任意一个小曲边梯形,用“直边”代替“曲边”(即在很小范围内以直代曲),有以下三种方案“以直代曲” 。
课题:曲边梯形面积
我行 我能 我要成功 我能成功
y = f(x)
b
a
x
y
O
S S1+ S2 + + Sn
将曲边梯形分成 n个小曲边梯形,并用小矩阵形的面积代替小曲边梯形的面积, 于是曲边梯形的面积S近似为
S1
Si
Sn
课题:曲边梯形面积
我行 我能 我要成功 我能成功
分割越细,面积的近似值就越精确。当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S。
下面用第一种方案“以直代曲”的具体操作过程
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(1)分割
把区间[0,1]等分成n个小区间:
过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(2) 以直代曲
(3)作和
课题:曲边梯形面积
我行 我能 我要成功 我能成功
(4)逼近
分割
以直代曲
作和
逼近
课题:曲边梯形面积
我行 我能 我要成功 我能成功
当分点非常多(n非常大)时,可以认为f(x)在小区间上几乎没有变化(或变化非常小),从而可以取小区间内任意一点xi对应的函数值f(xi)作为小矩形一边的长,于是f(xi) △x来近似表示小曲边梯形的面积
表示了曲边梯形面积的近似值
课题:曲边梯形面积
我行 我能 我要成功 我能成功
例1:火箭发射后ts的速度为v(t)(单位:m/s),假定0≤t≤10,对函数v(t)按上式所作的和具有怎样的实际意义?
例2:如图,有两个点电荷A、B,电量分别为qA,qB,,固定电荷A,将电荷B从距A为a处移到距A为b 处,求库仑力对电荷B所做的功。
课题:曲边梯形面积
我行 我能 我要成功 我能成功
