【数学】1.3.2《函数的极值与导数》课件(人教A版选修2-2)
文档属性
| 名称 | 【数学】1.3.2《函数的极值与导数》课件(人教A版选修2-2) |  | |
| 格式 | zip | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-11 16:40:25 | ||
图片预览




文档简介
(共13张PPT)
1.3.2函数的极值与导数
a
b
x
y
O
定义
一般地, 设函数 f (x) 在点x0附近有定义, 如果对x0附近的所有的点, 都有
我们就说 f (x0)是 f (x)
的一个极大值, 点x0叫做函数 y = f (x)的极大值点.
反之, 若 , 则称 f (x0) 是 f (x) 的一个极小值, 点x0叫做函数 y = f (x)的极小值点.
极小值点、极大值点统称为极值点, 极大值和极小值统称为极值.
y
a
b
x1
x2
x3
x4
O
x
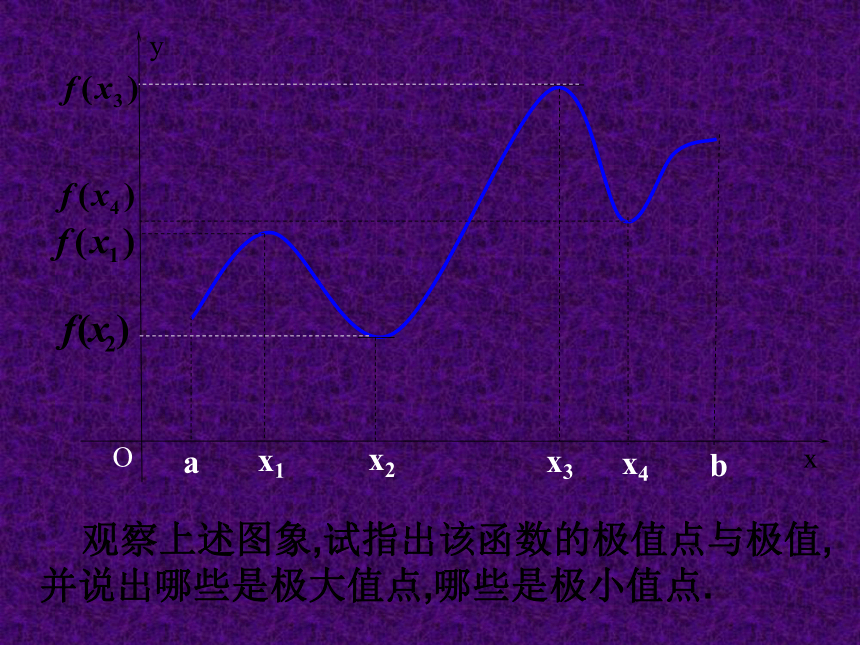
观察上述图象,试指出该函数的极值点与极值,并说出哪些是极大值点,哪些是极小值点.
(1)函数的极值是就函数在某一点附近的小区间而言的,在函数的整个定义区间内可能有多个极大值或极小值
(2)极大值不一定比极小值大
(3)可导函数f(x),点是极值点的必要条件是在该
点的导数为0
例:y=x3
练习1
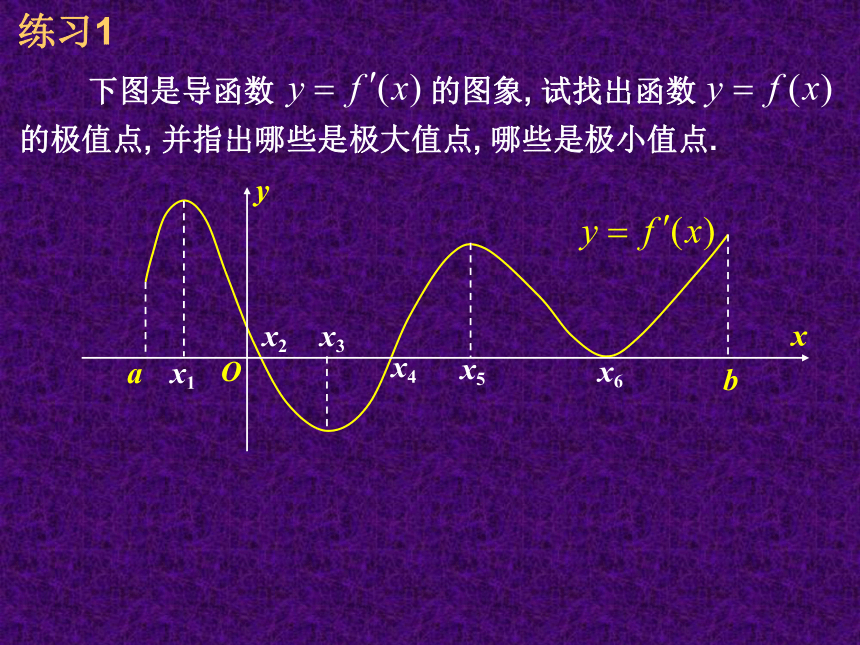
下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.
a
b
x
y
x1
O
x2
x3
x4
x5
x6
因为 所以
例1 求函数 的极值.
解:
令 解得 或
当 , 即 , 或 ;
当 , 即 .
当 x 变化时, f (x) 的变化情况如下表:
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –2 时, f (x)有极大值 28 / 3 ;
当 x = 2 时, f (x)有极小值 – 4 / 3 .
求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
练习2
求下列函数的极值:
解:
令 解得 列表:
x
0
f (x)
+
单调递增
单调递减
–
所以, 当 时, f (x)有极小值
练习2
求下列函数的极值:
解:
解得 列表:
x (–∞, –3) –3 (–3, 3) 3 ( 3, +∞)
0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –3 时, f (x)有极大值 54 ;
当 x = 3 时, f (x)有极小值 – 54 .
练习2
求下列函数的极值:
解:
解得
所以, 当 x = –2 时, f (x)有极小值 – 10 ;
当 x = 2 时, f (x)有极大值 22 .
解得
所以, 当 x = –1 时, f (x)有极小值 – 2 ;
当 x = 1 时, f (x)有极大值 2 .
习题 A组 #4
下图是导函数 的图象, 在标记的点中, 在哪一点处
(1)导函数 有极大值
(2)导函数 有极小值
(3)函数 有极大值
(4)函数 有极小值
或
1.3.2函数的极值与导数
a
b
x
y
O
定义
一般地, 设函数 f (x) 在点x0附近有定义, 如果对x0附近的所有的点, 都有
我们就说 f (x0)是 f (x)
的一个极大值, 点x0叫做函数 y = f (x)的极大值点.
反之, 若 , 则称 f (x0) 是 f (x) 的一个极小值, 点x0叫做函数 y = f (x)的极小值点.
极小值点、极大值点统称为极值点, 极大值和极小值统称为极值.
y
a
b
x1
x2
x3
x4
O
x
观察上述图象,试指出该函数的极值点与极值,并说出哪些是极大值点,哪些是极小值点.
(1)函数的极值是就函数在某一点附近的小区间而言的,在函数的整个定义区间内可能有多个极大值或极小值
(2)极大值不一定比极小值大
(3)可导函数f(x),点是极值点的必要条件是在该
点的导数为0
例:y=x3
练习1
下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.
a
b
x
y
x1
O
x2
x3
x4
x5
x6
因为 所以
例1 求函数 的极值.
解:
令 解得 或
当 , 即 , 或 ;
当 , 即 .
当 x 变化时, f (x) 的变化情况如下表:
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –2 时, f (x)有极大值 28 / 3 ;
当 x = 2 时, f (x)有极小值 – 4 / 3 .
求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
练习2
求下列函数的极值:
解:
令 解得 列表:
x
0
f (x)
+
单调递增
单调递减
–
所以, 当 时, f (x)有极小值
练习2
求下列函数的极值:
解:
解得 列表:
x (–∞, –3) –3 (–3, 3) 3 ( 3, +∞)
0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –3 时, f (x)有极大值 54 ;
当 x = 3 时, f (x)有极小值 – 54 .
练习2
求下列函数的极值:
解:
解得
所以, 当 x = –2 时, f (x)有极小值 – 10 ;
当 x = 2 时, f (x)有极大值 22 .
解得
所以, 当 x = –1 时, f (x)有极小值 – 2 ;
当 x = 1 时, f (x)有极大值 2 .
习题 A组 #4
下图是导函数 的图象, 在标记的点中, 在哪一点处
(1)导函数 有极大值
(2)导函数 有极小值
(3)函数 有极大值
(4)函数 有极小值
或
