【数学】1.3.3《函数的最值》课件(人教A版选修2-2)
文档属性
| 名称 | 【数学】1.3.3《函数的最值》课件(人教A版选修2-2) |  | |
| 格式 | zip | ||
| 文件大小 | 36.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-11 16:40:25 | ||
图片预览




文档简介
(共11张PPT)
一、复习与引入
1.当函数f(x)在x0处连续时,判别f(x0)是极大(小)值的方
法是:
①如果在x0附近的左侧 右侧 ,那么,f(x0)
是极大值;
②如果在x0附近的左侧 右侧 ,那么,f(x0)
是极小值.
2.导数为零的点是该点为极值点的必要条件,而不是充
分条件.极值只能在函数不可导的点或导数为零的点
取到.
3.在某些问题中,往往关心的是函数在一个定义区间上,
哪个值最大,哪个值最小,而不是极值.
二、新课——函数的最值
x
X2
o
a
X3
b
x1
y
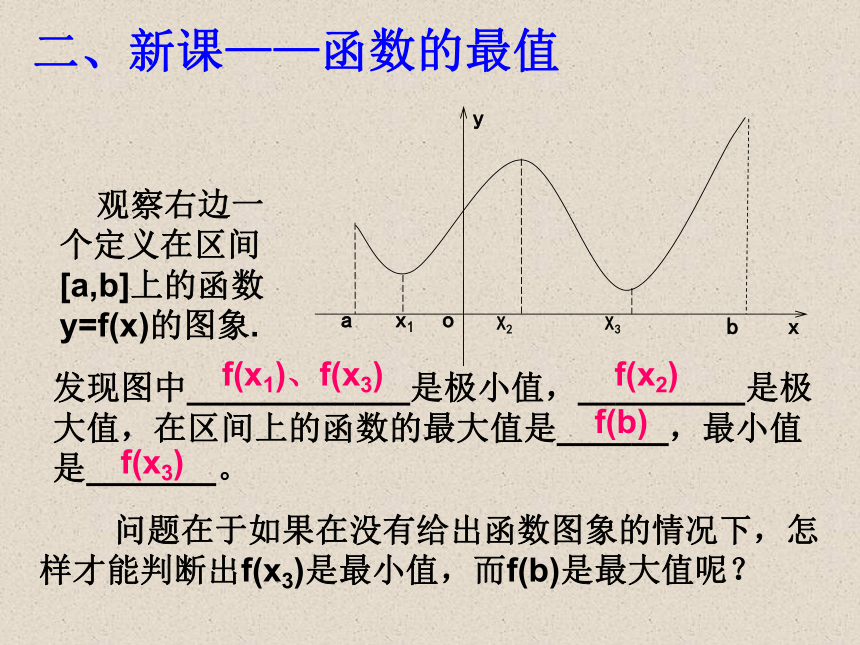
观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.
发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______。
f(x1)、f(x3)
f(x2)
f(b)
f(x3)
问题在于如果在没有给出函数图象的情况下,怎样才能判断出f(x3)是最小值,而f(b)是最大值呢?
导数的应用-----求函数最值.
(2)将y=f(x)的各极值与f(a)、f(b)(端点处)比较,其中最大的一个为最大值,最小的一个为最小值.
求f(x)在闭区间[a,b]上的最值的步骤
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
求函数的最值时,应注意以下几点:
(1)函数的极值是在局部范围内讨论问题,是一个局部概念,而函数的最值是对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.
(3)函数在其定义域上的最大值与最小值至多各有一个, 而函数的极值则可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值).
三、例题选讲
例1:求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.
解:
令 ,解得x=-1,0,1.
当x变化时, 的变化情况如下表:
x -2 (-2,-1) -1 (-1,0) 0 (0,1) 1 (1,2) 2
y’ - 0 + 0 - 0 +
y 13 ↘ 4 ↗ 5 ↘ 4 ↗ 13
从上表可知,最大值是13,最小值是4.
例2、函数 y = x + 3 x -9x在 [-4 , 4 ]上的最大值为 ,最小值为 .
分析: (1) 由 f (x)=3x +6x-9=0,
(2) 区间[-4 , 4 ]端点处的函数值为
f (-4) =20 , f (4) =76
得x1=-3,x2=1
函数值为f (-3)=27, f (1)=-5
当x变化时,y′ 、 y的变化情况如下表:
x -4 (-4,-3) -3 (-3,1) 1 (1,4) 4
y′ + 0 - 0 + 0
y 20 27 -5 76
比较以上各函数值,
可知函数在[-4 , 4 ]上的最大值为 f (4) =76,
最小值为 f (1)=-5
求下列函数在指定区间内的最大值和最小值:
练习:
最大值 f (-1)=3,最小值 f (3)= -61
(04浙江文21)(本题满分12分)
已知a为实数,
(Ⅰ)求导数 ;
(Ⅱ)若 ,求 在[-2,2]上的最大值和最小值;
(Ⅲ)若 在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
例3
五、小结
1.求在[a,b]上连续,(a,b)上可导的函数f(x)在[a,b]上的
最值的步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a)、f(b)比较,其中最大的一个
是最大值,最小的一个是最小值.
2.求函数的最值时,应注意以下几点:
(1)要正确区分极值与最值这两个概念.
(2)在[a,b]上连续,(a,b)上可导的函数f(x)在(a,b)内未
必有最大值与最小值.
(3)一旦给出的函数在(a,b)上有个别不可导点的话,不
要忘记在步骤(2)中,要把这些点的函数值与各极值
和f(a)、f(b)放在一起比较.
一、复习与引入
1.当函数f(x)在x0处连续时,判别f(x0)是极大(小)值的方
法是:
①如果在x0附近的左侧 右侧 ,那么,f(x0)
是极大值;
②如果在x0附近的左侧 右侧 ,那么,f(x0)
是极小值.
2.导数为零的点是该点为极值点的必要条件,而不是充
分条件.极值只能在函数不可导的点或导数为零的点
取到.
3.在某些问题中,往往关心的是函数在一个定义区间上,
哪个值最大,哪个值最小,而不是极值.
二、新课——函数的最值
x
X2
o
a
X3
b
x1
y
观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.
发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______。
f(x1)、f(x3)
f(x2)
f(b)
f(x3)
问题在于如果在没有给出函数图象的情况下,怎样才能判断出f(x3)是最小值,而f(b)是最大值呢?
导数的应用-----求函数最值.
(2)将y=f(x)的各极值与f(a)、f(b)(端点处)比较,其中最大的一个为最大值,最小的一个为最小值.
求f(x)在闭区间[a,b]上的最值的步骤
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
求函数的最值时,应注意以下几点:
(1)函数的极值是在局部范围内讨论问题,是一个局部概念,而函数的最值是对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.
(3)函数在其定义域上的最大值与最小值至多各有一个, 而函数的极值则可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值).
三、例题选讲
例1:求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.
解:
令 ,解得x=-1,0,1.
当x变化时, 的变化情况如下表:
x -2 (-2,-1) -1 (-1,0) 0 (0,1) 1 (1,2) 2
y’ - 0 + 0 - 0 +
y 13 ↘ 4 ↗ 5 ↘ 4 ↗ 13
从上表可知,最大值是13,最小值是4.
例2、函数 y = x + 3 x -9x在 [-4 , 4 ]上的最大值为 ,最小值为 .
分析: (1) 由 f (x)=3x +6x-9=0,
(2) 区间[-4 , 4 ]端点处的函数值为
f (-4) =20 , f (4) =76
得x1=-3,x2=1
函数值为f (-3)=27, f (1)=-5
当x变化时,y′ 、 y的变化情况如下表:
x -4 (-4,-3) -3 (-3,1) 1 (1,4) 4
y′ + 0 - 0 + 0
y 20 27 -5 76
比较以上各函数值,
可知函数在[-4 , 4 ]上的最大值为 f (4) =76,
最小值为 f (1)=-5
求下列函数在指定区间内的最大值和最小值:
练习:
最大值 f (-1)=3,最小值 f (3)= -61
(04浙江文21)(本题满分12分)
已知a为实数,
(Ⅰ)求导数 ;
(Ⅱ)若 ,求 在[-2,2]上的最大值和最小值;
(Ⅲ)若 在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
例3
五、小结
1.求在[a,b]上连续,(a,b)上可导的函数f(x)在[a,b]上的
最值的步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a)、f(b)比较,其中最大的一个
是最大值,最小的一个是最小值.
2.求函数的最值时,应注意以下几点:
(1)要正确区分极值与最值这两个概念.
(2)在[a,b]上连续,(a,b)上可导的函数f(x)在(a,b)内未
必有最大值与最小值.
(3)一旦给出的函数在(a,b)上有个别不可导点的话,不
要忘记在步骤(2)中,要把这些点的函数值与各极值
和f(a)、f(b)放在一起比较.
