【数学】1.7.1《定积分在几何中的简单应用》课件(人教A版选修2-2)
文档属性
| 名称 | 【数学】1.7.1《定积分在几何中的简单应用》课件(人教A版选修2-2) |

|
|
| 格式 | zip | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-11 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
1.7.1定积分在几何中的简单应用
定积分的简单应用
1、定积分的几何意义:
O
x
y
a
b
y f (x)
x=a、x=b与 x轴所围成的曲边梯形的面积。
x
y
O
a
b
y f (x)
=-S
当f(x) 0时,由y f (x)、x a、x b 与 x 轴所围成的曲边梯形位于 x 轴的下方,
一、复习回顾
定理 (微积分基本定理)
2、牛顿—莱布尼茨公式
如果f(x)是区间[a,b]上的连续函数,
并且F’(x)=f(x),则
一、复习回顾
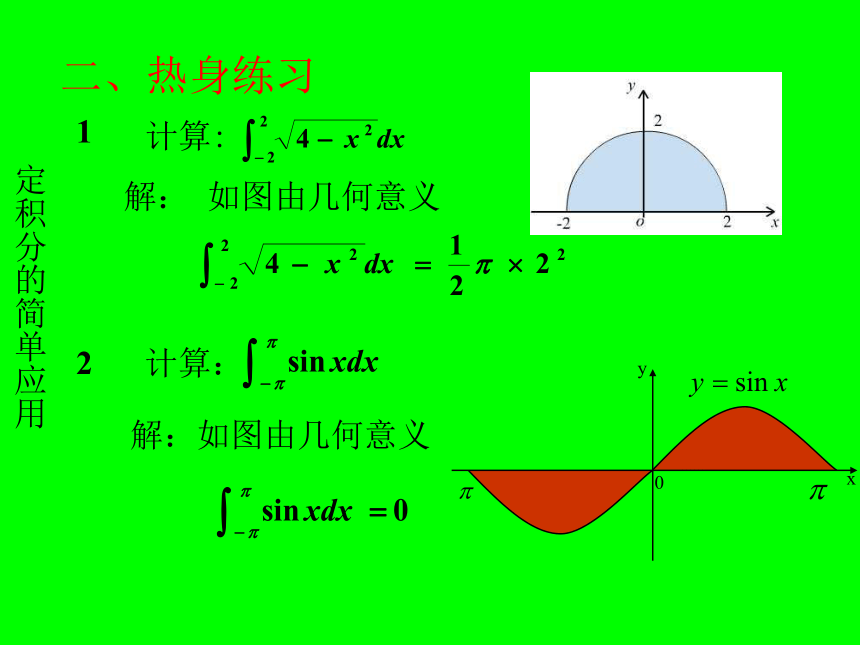
二、热身练习
1
解: 如图由几何意义
2
计算:
计算:
解:如图由几何意义
定积分的简单应用
0
y
x
定积分的简单应用
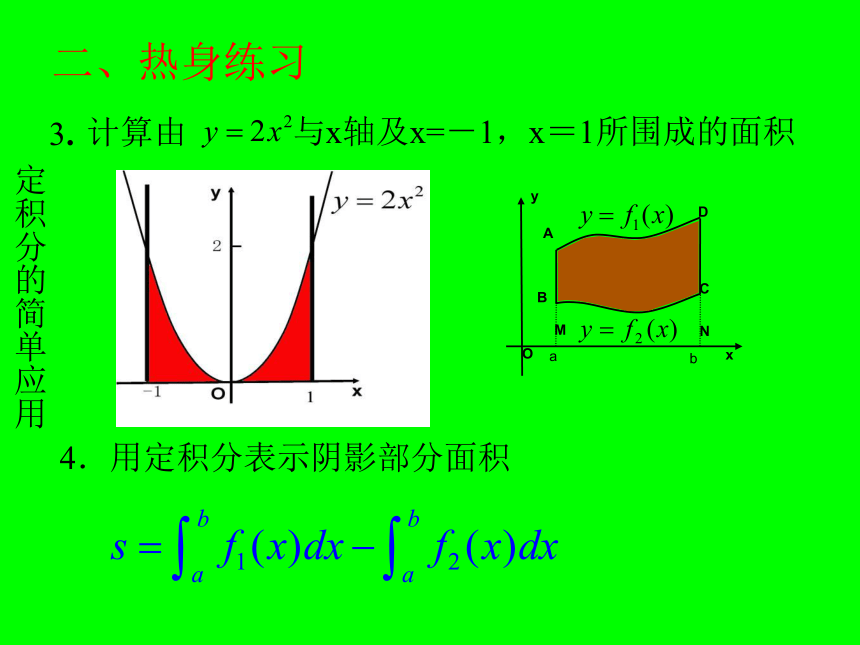
3.
计算由
与x轴及x=-1,x=1所围成的面积
x
y
N
M
O
a
b
A
B
C
D
4.用定积分表示阴影部分面积
二、热身练习
A2
a
b
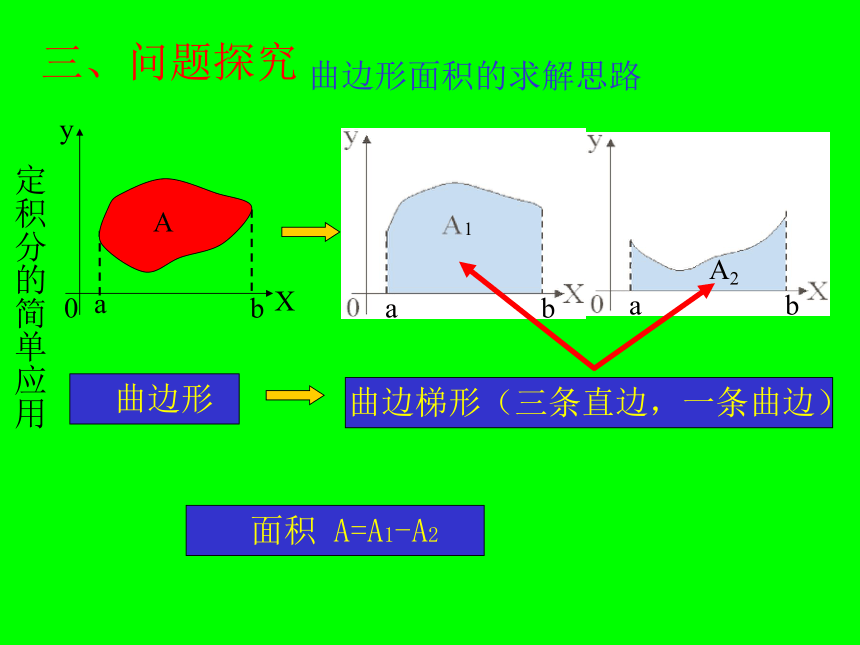
曲边梯形(三条直边,一条曲边)
a
b
X
A
0
y
曲边形
面积 A=A1-A2
a
b
1
三、问题探究
曲边形面积的求解思路
定积分的简单应用
四、例题实践求曲边形面积
例1.计算由曲线
与
所围图形的面积
解:作出草图,所求面积为阴影部分的面积
解方程组
得交点横坐标为
及
S=S曲边梯形OABC-S曲边梯形OABD
=
=
=
=
定积分的简单应用
A
B
C
D
x
y
O
1
1
-1
-1
归纳
求由曲线围成的平面图形面积的解题步骤:
(1)画草图,求出曲线的交点坐标
(3)确定被积函数及积分区间
(4)计算定积分,求出面积
定积分的简单应用
(2)将曲边形面积转化为曲边梯形面积
4
x
y
O
8
4
2
2
B
S1
S2
A:
4
y
O
8
4
2
2
A
S1
S2
例2.计算由曲线
直线
以及x轴
所围图形的面积S
定积分的简单应用
四、例题实践求曲边形面积
B:
x
y
O
1
五、巩固练习书本P58练习
提高:书本P66复习参考题A组16题
定积分的简单应用
求曲线
与直线
所围成平面图形的面积
S1
解题要点:
S2
有其他方法吗?
S1=S2
七、作业
1、书本P60 习题A组1 B组3
2、全优设计P48-49
3、思考B组1,2
六、小结
1.本节课我们做了什么探究活动呢?
2.如何用定积分解决曲边形面积问题呢?
3.解题时应注意些什么呢?
4.体会到什么样的数学研究思路及方法呢?
思考
h
b
如图, 一桥拱的形状为抛 物线, 已知该抛物线拱的高为 常数h, 宽为常数b.
求证: 抛物线拱的面积
定积分的简单应用
建立平面直角坐标系 确定抛物线方程
求由曲线围成的平面图形面积的解题步骤
课本P60 习题B组2
x
h
b
y
0
证明:如图建立平面直角坐标系,可设抛物线方程为
则有
得
所以抛物线方程为
于是,抛物线拱的面积为
代抛物线上一点入方程
S
2S
定积分的简单应用
1.7.1定积分在几何中的简单应用
定积分的简单应用
1、定积分的几何意义:
O
x
y
a
b
y f (x)
x=a、x=b与 x轴所围成的曲边梯形的面积。
x
y
O
a
b
y f (x)
=-S
当f(x) 0时,由y f (x)、x a、x b 与 x 轴所围成的曲边梯形位于 x 轴的下方,
一、复习回顾
定理 (微积分基本定理)
2、牛顿—莱布尼茨公式
如果f(x)是区间[a,b]上的连续函数,
并且F’(x)=f(x),则
一、复习回顾
二、热身练习
1
解: 如图由几何意义
2
计算:
计算:
解:如图由几何意义
定积分的简单应用
0
y
x
定积分的简单应用
3.
计算由
与x轴及x=-1,x=1所围成的面积
x
y
N
M
O
a
b
A
B
C
D
4.用定积分表示阴影部分面积
二、热身练习
A2
a
b
曲边梯形(三条直边,一条曲边)
a
b
X
A
0
y
曲边形
面积 A=A1-A2
a
b
1
三、问题探究
曲边形面积的求解思路
定积分的简单应用
四、例题实践求曲边形面积
例1.计算由曲线
与
所围图形的面积
解:作出草图,所求面积为阴影部分的面积
解方程组
得交点横坐标为
及
S=S曲边梯形OABC-S曲边梯形OABD
=
=
=
=
定积分的简单应用
A
B
C
D
x
y
O
1
1
-1
-1
归纳
求由曲线围成的平面图形面积的解题步骤:
(1)画草图,求出曲线的交点坐标
(3)确定被积函数及积分区间
(4)计算定积分,求出面积
定积分的简单应用
(2)将曲边形面积转化为曲边梯形面积
4
x
y
O
8
4
2
2
B
S1
S2
A:
4
y
O
8
4
2
2
A
S1
S2
例2.计算由曲线
直线
以及x轴
所围图形的面积S
定积分的简单应用
四、例题实践求曲边形面积
B:
x
y
O
1
五、巩固练习书本P58练习
提高:书本P66复习参考题A组16题
定积分的简单应用
求曲线
与直线
所围成平面图形的面积
S1
解题要点:
S2
有其他方法吗?
S1=S2
七、作业
1、书本P60 习题A组1 B组3
2、全优设计P48-49
3、思考B组1,2
六、小结
1.本节课我们做了什么探究活动呢?
2.如何用定积分解决曲边形面积问题呢?
3.解题时应注意些什么呢?
4.体会到什么样的数学研究思路及方法呢?
思考
h
b
如图, 一桥拱的形状为抛 物线, 已知该抛物线拱的高为 常数h, 宽为常数b.
求证: 抛物线拱的面积
定积分的简单应用
建立平面直角坐标系 确定抛物线方程
求由曲线围成的平面图形面积的解题步骤
课本P60 习题B组2
x
h
b
y
0
证明:如图建立平面直角坐标系,可设抛物线方程为
则有
得
所以抛物线方程为
于是,抛物线拱的面积为
代抛物线上一点入方程
S
2S
定积分的简单应用
