中考数学:和值复习之直线型问题
图片预览



文档简介
李中池
直线型问题
直线型问题是几何部分的重要内容,它包括三角形问题,四边形问题。图形的全等与相似问题,解直角三角形问题等内容。在几何的知识结构里处于基础地位,而且能较好的考察学生的空间想象能力及思维能力,是最近几年的中考的必考内容。这部分对学生推理能力要求的不是很高,但对学生的观察、比较、归纳、猜想和动手操作等方面要求较高。
第一、三角形问题
例1、2010年福建晋江)如图,在等边中,线段为边上的中线. 动点在直线上时,以为一边且在的下方作等边,连结.
(1) 填空:度;
(2) 当点在线段上(点不运动到点)时,试求出的值;
(3)若,以点为圆心,以5为半径作⊙与直线相交于点、两点,在点运动的过程中(点与点重合除外),试求的长.
注意
本题中的第三问,图形比较复杂,首先要考虑从复杂的几何图形中分离出简单的基本图形,同时要考虑点D所在的三种位置时对问题带来的影响。
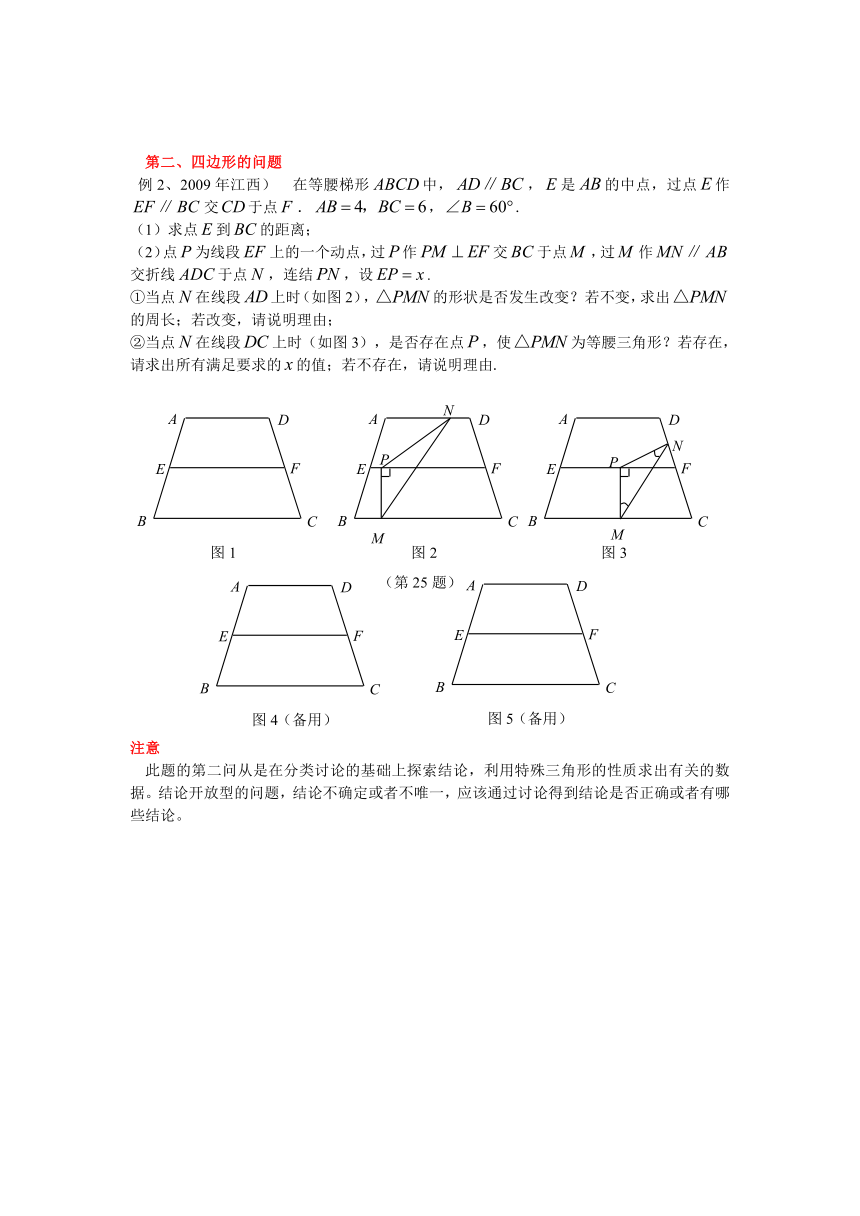
第二、四边形的问题
例2、2009年江西) 在等腰梯形中,,是的中点,过点作交于点.,.
(1)求点到的距离;
(2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设.
①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的周长;若改变,请说明理由;
②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由.
注意
此题的第二问从是在分类讨论的基础上探索结论,利用特殊三角形的性质求出有关的数据。结论开放型的问题,结论不确定或者不唯一,应该通过讨论得到结论是否正确或者有哪些结论。
相似型的问题
例3、 2010年江苏淮安)如题28(a)图,在平面直角坐标系中,点A坐标为(12,0),点B坐标为(6,8),点C为OB的中点,点D从点O出发,沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周.
(1)点C坐标是( , ),当点D运动8.5秒时所在位置的坐标是( , );
(2)设点D运动的时间为t秒,试用含t的代数式表示△OCD的面积S,并指出t为何值
时,S最大;
(3)点E在线段AB上以同样速度由点A向点B运动,如题28(b)图,若点E与点D同时
出发,问在运动5秒钟内,以点D,A,E为顶点的三角形何时与△OCD相似(只考虑以
点A.O为对应顶点的情况):
题28(a)图 题28(b)图
注意
此题第二问的做题方法,有多个,比如用同一锐角间的正弦余弦的平方和等于1,求的角OBA的正弦值,从而可求的三角形OC边上的高,直接求的S
再如常规的方法,转化成几个可求面积之和或差。
直线型图形与抛物线问题
例4、2010年甘肃嘉峪关)如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与相似?若存在,请确定符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
练习
1.如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动) .
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立 若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立 若成立 请直接写出结论,不必证明或说明理由.
2如图,在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P、Q分别从A、C两点同时出发,其中点P以1cm/s的速度沿AC向终点C移动;点Q以cm/s的速度沿CB向终点B移动.过P作PE∥CB交AD于点E,设动点的运动时间为x秒.
(1)用含 x的代数式表示EP;
(2)当Q在线段CD上运动几秒时,四边形PEDQ是平行四边形;
(3)当Q在线段BD(不包括点B、点D)上运动时,求四边形EPDQ面积的最大值.
3正方形边长为4,、分别是、上的两个动点,当点在上运动时,保持和垂直,
(1)证明:;
(2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积;
(3)当点运动到什么位置时,求的值.
4如图,抛物线y=ax2+bx+c经过点A(4,0)、B(2,2),连结OB、AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此抛物线上,并说明理由.
1(1)判断:EN与MF相等 (或EN=MF),点F在直线NE上, 3分
(说明:答对一个给2分)
(2)成立. 4分
证明:
法一:连结DE,DF. 5分
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点,
∴DE,DF,EF为三角形的中位线.∴DE=DF=EF,∠ FDE=60°.
又∠MDF+∠FDN=60°, ∠NDE+∠FDN=60°,
∴∠MDF=∠NDE. 7分
在△DMF和△DNE中,DF=DE,DM=DN, ∠MDF=∠NDE,
∴△DMF≌△DNE. 8分
∴MF=NE. 9分
法二:
延长EN,则EN过点F. 5分
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点, ∴EF=DF=BF.
∵∠BDM+∠MDF=60°, ∠FDN+∠MDF=60°,
∴∠BDM=∠FDN. 7分
又∵DM=DN, ∠ABM=∠DFN=60°,
∴△DBM≌△DFN. 8分
∴BM=FN.
∵BF=EF, ∴MF=EN. 9分
法三:
连结DF,NF. 5分
∵△ABC是等边三角形,
∴AC=BC=AC.
又∵D,E,F是三边的中点,
∴DF为三角形的中位线,∴DF=AC=AB=DB.
又∠BDM+∠MDF=60°, ∠NDF+∠MDF=60°,
∴∠BDM=∠FDN. 7分
在△DBM和△DFN中,DF=DB,
DM=DN, ∠BDM=∠NDF,∴△DBM≌△DFN.
∴∠B=∠DFN=60°. 8分
又∵△DEF是△ABC各边中点所构成的三角形,
∴∠DFE=60°.
∴可得点N在EF上,
∴MF=EN. 9分
(3)画出图形(连出线段NE), 11分
MF与EN相等的结论仍然成立(或MF=NE成立). 12分
2解:(1)∵PE∥CB,∴∠AEP=∠ADC
又∵∠EAP=∠DAC,∴△AEP∽△ADC
……………………………………2分
∴,∴…………3分
∴.…………………………4分
(2)由四边形PEDQ1是平行四边形,
可得EP=DQ1.………………………5分
即,
所以.…………………………6分
∵0 < x < 2.4……………………………7分
∴当Q在线段CD上运动1.5秒时,四边形PEDQ是平行四边形.……8分
(3)……………………9分
………………………………10分
又∵2.4 < x < 4,………………………………………………12分
∴当时,S取得最大值,最大值为.………
3解:(1)在正方形中,,
,
,
.
在中,,
,
. 2分
(2),
,
, 4分
,
当时,取最大值,最大值为10. 6分
(3),
要使,必须有, 7分
由(1)知,
,
当点运动到的中点时,,此时. 9分
(其它正确的解法,参照评分建议按步给分)
4
A
B
C
备用图(1)
A
B
C
备用图(2)
A
D
E
B
F
C
图4(备用)
A
D
E
B
F
C
图5(备用)
A
D
E
B
F
C
图1
图2
A
D
E
B
F
C
P
N
M
图3
A
D
E
B
F
C
P
N
M
(第25题)
图①
图②
图③
第25题图
A
·
B
C
D
E
F
·
·
·
N
D
A
CD
B
M
第22题图
第22题
A
B
x
O
y
N
C
A
B
F
M
D
E
N
C
A
B
F
M
D
E
N
D
A
CD
B
M
答案22题图
直线型问题
直线型问题是几何部分的重要内容,它包括三角形问题,四边形问题。图形的全等与相似问题,解直角三角形问题等内容。在几何的知识结构里处于基础地位,而且能较好的考察学生的空间想象能力及思维能力,是最近几年的中考的必考内容。这部分对学生推理能力要求的不是很高,但对学生的观察、比较、归纳、猜想和动手操作等方面要求较高。
第一、三角形问题
例1、2010年福建晋江)如图,在等边中,线段为边上的中线. 动点在直线上时,以为一边且在的下方作等边,连结.
(1) 填空:度;
(2) 当点在线段上(点不运动到点)时,试求出的值;
(3)若,以点为圆心,以5为半径作⊙与直线相交于点、两点,在点运动的过程中(点与点重合除外),试求的长.
注意
本题中的第三问,图形比较复杂,首先要考虑从复杂的几何图形中分离出简单的基本图形,同时要考虑点D所在的三种位置时对问题带来的影响。
第二、四边形的问题
例2、2009年江西) 在等腰梯形中,,是的中点,过点作交于点.,.
(1)求点到的距离;
(2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设.
①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的周长;若改变,请说明理由;
②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由.
注意
此题的第二问从是在分类讨论的基础上探索结论,利用特殊三角形的性质求出有关的数据。结论开放型的问题,结论不确定或者不唯一,应该通过讨论得到结论是否正确或者有哪些结论。
相似型的问题
例3、 2010年江苏淮安)如题28(a)图,在平面直角坐标系中,点A坐标为(12,0),点B坐标为(6,8),点C为OB的中点,点D从点O出发,沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周.
(1)点C坐标是( , ),当点D运动8.5秒时所在位置的坐标是( , );
(2)设点D运动的时间为t秒,试用含t的代数式表示△OCD的面积S,并指出t为何值
时,S最大;
(3)点E在线段AB上以同样速度由点A向点B运动,如题28(b)图,若点E与点D同时
出发,问在运动5秒钟内,以点D,A,E为顶点的三角形何时与△OCD相似(只考虑以
点A.O为对应顶点的情况):
题28(a)图 题28(b)图
注意
此题第二问的做题方法,有多个,比如用同一锐角间的正弦余弦的平方和等于1,求的角OBA的正弦值,从而可求的三角形OC边上的高,直接求的S
再如常规的方法,转化成几个可求面积之和或差。
直线型图形与抛物线问题
例4、2010年甘肃嘉峪关)如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与相似?若存在,请确定符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
练习
1.如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动) .
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立 若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立 若成立 请直接写出结论,不必证明或说明理由.
2如图,在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P、Q分别从A、C两点同时出发,其中点P以1cm/s的速度沿AC向终点C移动;点Q以cm/s的速度沿CB向终点B移动.过P作PE∥CB交AD于点E,设动点的运动时间为x秒.
(1)用含 x的代数式表示EP;
(2)当Q在线段CD上运动几秒时,四边形PEDQ是平行四边形;
(3)当Q在线段BD(不包括点B、点D)上运动时,求四边形EPDQ面积的最大值.
3正方形边长为4,、分别是、上的两个动点,当点在上运动时,保持和垂直,
(1)证明:;
(2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积;
(3)当点运动到什么位置时,求的值.
4如图,抛物线y=ax2+bx+c经过点A(4,0)、B(2,2),连结OB、AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此抛物线上,并说明理由.
1(1)判断:EN与MF相等 (或EN=MF),点F在直线NE上, 3分
(说明:答对一个给2分)
(2)成立. 4分
证明:
法一:连结DE,DF. 5分
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点,
∴DE,DF,EF为三角形的中位线.∴DE=DF=EF,∠ FDE=60°.
又∠MDF+∠FDN=60°, ∠NDE+∠FDN=60°,
∴∠MDF=∠NDE. 7分
在△DMF和△DNE中,DF=DE,DM=DN, ∠MDF=∠NDE,
∴△DMF≌△DNE. 8分
∴MF=NE. 9分
法二:
延长EN,则EN过点F. 5分
∵△ABC是等边三角形, ∴AB=AC=BC.
又∵D,E,F是三边的中点, ∴EF=DF=BF.
∵∠BDM+∠MDF=60°, ∠FDN+∠MDF=60°,
∴∠BDM=∠FDN. 7分
又∵DM=DN, ∠ABM=∠DFN=60°,
∴△DBM≌△DFN. 8分
∴BM=FN.
∵BF=EF, ∴MF=EN. 9分
法三:
连结DF,NF. 5分
∵△ABC是等边三角形,
∴AC=BC=AC.
又∵D,E,F是三边的中点,
∴DF为三角形的中位线,∴DF=AC=AB=DB.
又∠BDM+∠MDF=60°, ∠NDF+∠MDF=60°,
∴∠BDM=∠FDN. 7分
在△DBM和△DFN中,DF=DB,
DM=DN, ∠BDM=∠NDF,∴△DBM≌△DFN.
∴∠B=∠DFN=60°. 8分
又∵△DEF是△ABC各边中点所构成的三角形,
∴∠DFE=60°.
∴可得点N在EF上,
∴MF=EN. 9分
(3)画出图形(连出线段NE), 11分
MF与EN相等的结论仍然成立(或MF=NE成立). 12分
2解:(1)∵PE∥CB,∴∠AEP=∠ADC
又∵∠EAP=∠DAC,∴△AEP∽△ADC
……………………………………2分
∴,∴…………3分
∴.…………………………4分
(2)由四边形PEDQ1是平行四边形,
可得EP=DQ1.………………………5分
即,
所以.…………………………6分
∵0 < x < 2.4……………………………7分
∴当Q在线段CD上运动1.5秒时,四边形PEDQ是平行四边形.……8分
(3)……………………9分
………………………………10分
又∵2.4 < x < 4,………………………………………………12分
∴当时,S取得最大值,最大值为.………
3解:(1)在正方形中,,
,
,
.
在中,,
,
. 2分
(2),
,
, 4分
,
当时,取最大值,最大值为10. 6分
(3),
要使,必须有, 7分
由(1)知,
,
当点运动到的中点时,,此时. 9分
(其它正确的解法,参照评分建议按步给分)
4
A
B
C
备用图(1)
A
B
C
备用图(2)
A
D
E
B
F
C
图4(备用)
A
D
E
B
F
C
图5(备用)
A
D
E
B
F
C
图1
图2
A
D
E
B
F
C
P
N
M
图3
A
D
E
B
F
C
P
N
M
(第25题)
图①
图②
图③
第25题图
A
·
B
C
D
E
F
·
·
·
N
D
A
CD
B
M
第22题图
第22题
A
B
x
O
y
N
C
A
B
F
M
D
E
N
C
A
B
F
M
D
E
N
D
A
CD
B
M
答案22题图
同课章节目录
