人教版八年级上册12.2 三角形全等的判定暑期练习(word含答案)
文档属性
| 名称 | 人教版八年级上册12.2 三角形全等的判定暑期练习(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 20:34:20 | ||
图片预览

文档简介
12.2
三角形全等的判定暑期练习
一、选择题
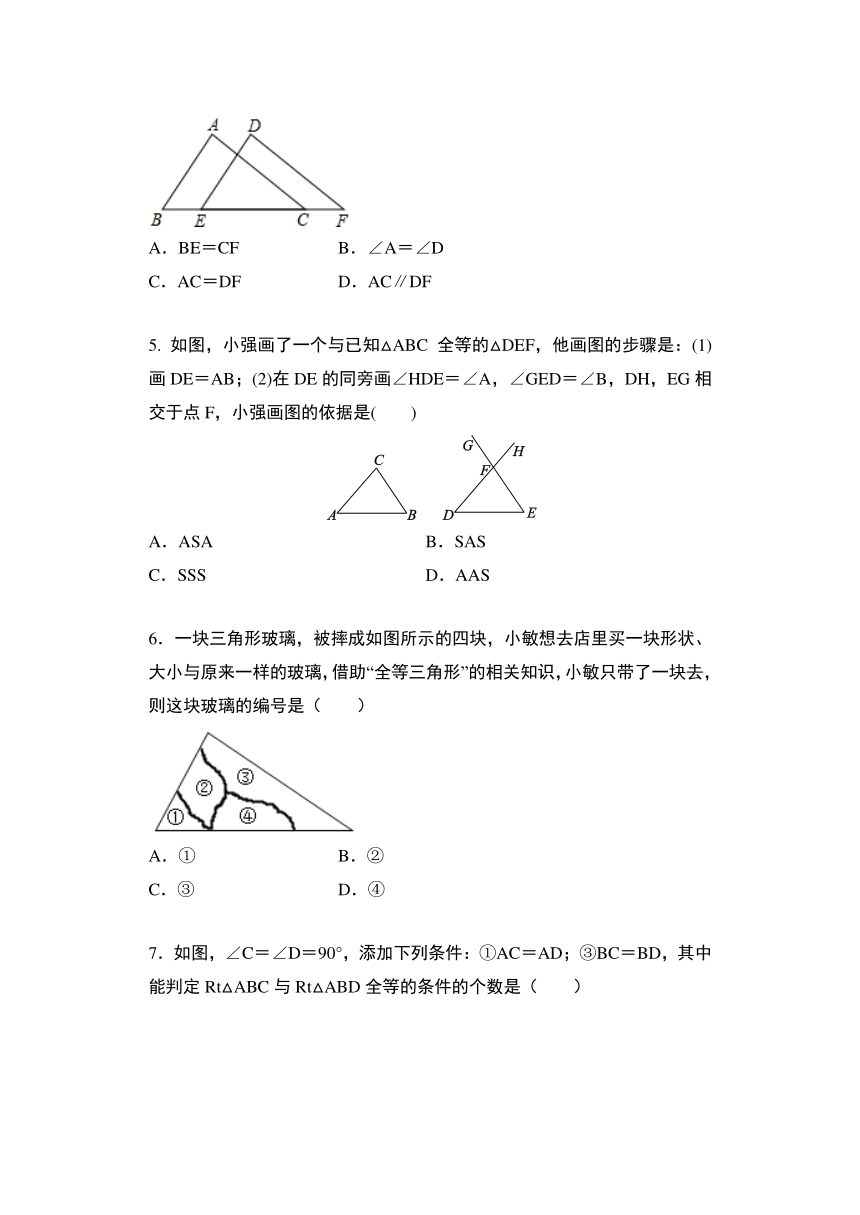
1.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是(
)
A.△ADC≌△BCD
B.△ABD≌△BAC
C.△AOB≌△COD
D.△AOD≌△BOC
2.如图,在△ABC中,∠B=40°,AF=CD,AE=CF( )
A.50°
B.60°
C.70°
D.80°
3.
如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是
( )
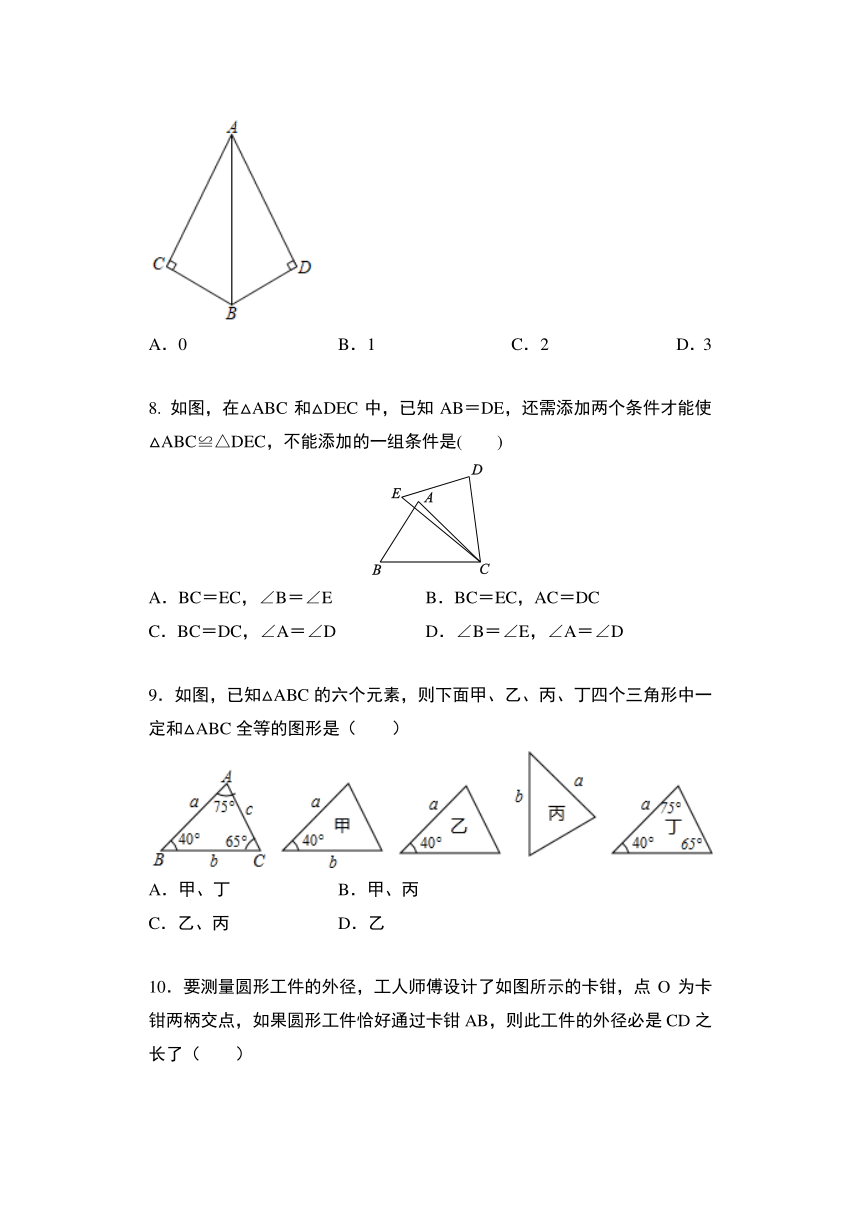
4.如图,△ABC和△DEF中,AB=DE,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF
B.∠A=∠D
C.AC=DF
D.AC∥DF
5.
如图,小强画了一个与已知△ABC全等的△DEF,他画图的步骤是:(1)画DE=AB;(2)在DE的同旁画∠HDE=∠A,∠GED=∠B,DH,EG相交于点F,小强画图的依据是( )
A.ASA
B.SAS
C.SSS
D.AAS
6.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A.①
B.②
C.③
D.④
7.如图,∠C=∠D=90°,添加下列条件:①AC=AD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.0
B.1
C.2
D.3
8.
如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
9.如图,已知△ABC的六个元素,则下面甲、乙、丙、丁四个三角形中一定和△ABC全等的图形是( )
A.甲、丁
B.甲、丙
C.乙、丙
D.乙
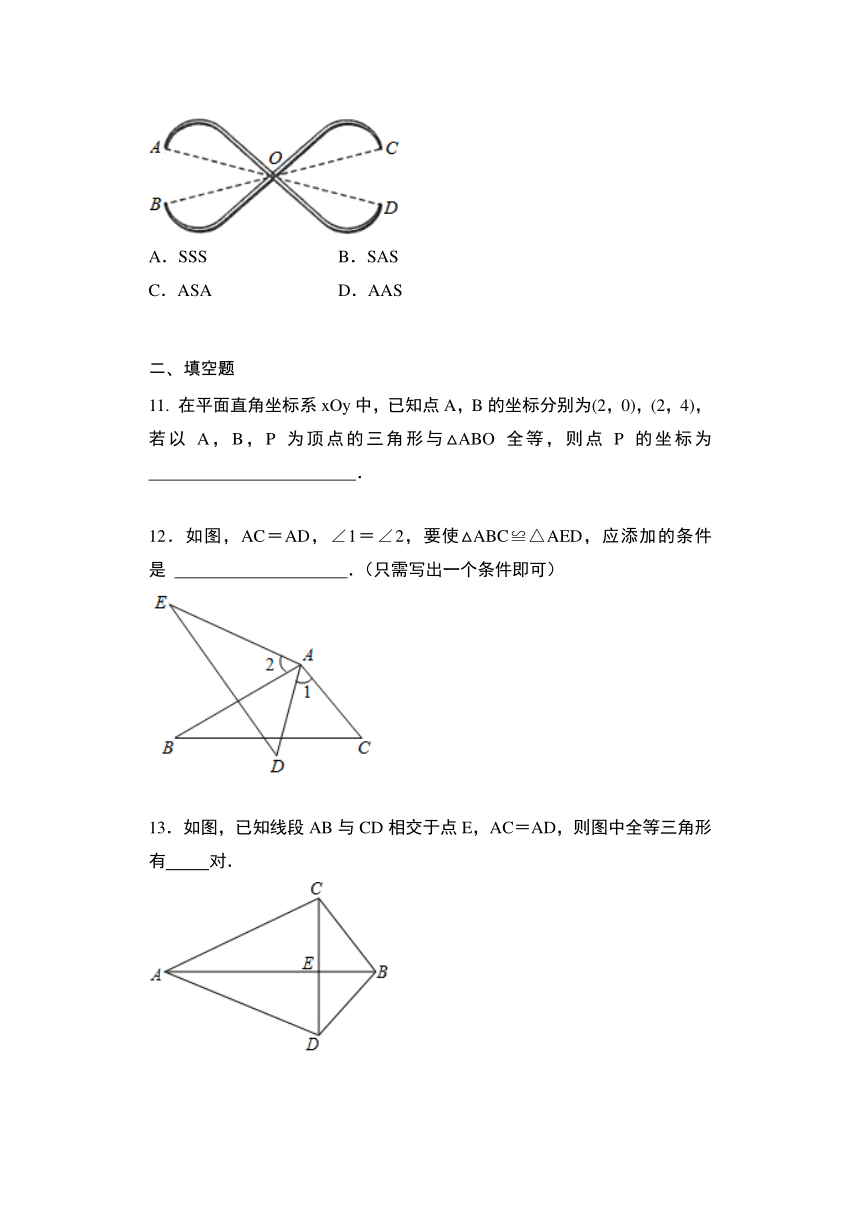
10.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了( )
A.SSS
B.SAS
C.ASA
D.AAS
二、填空题
11.
在平面直角坐标系xOy中,已知点A,B的坐标分别为(2,0),(2,4),若以A,B,P为顶点的三角形与△ABO全等,则点P的坐标为________________________.
12.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是
.(只需写出一个条件即可)
13.如图,已知线段AB与CD相交于点E,AC=AD,则图中全等三角形有
对.
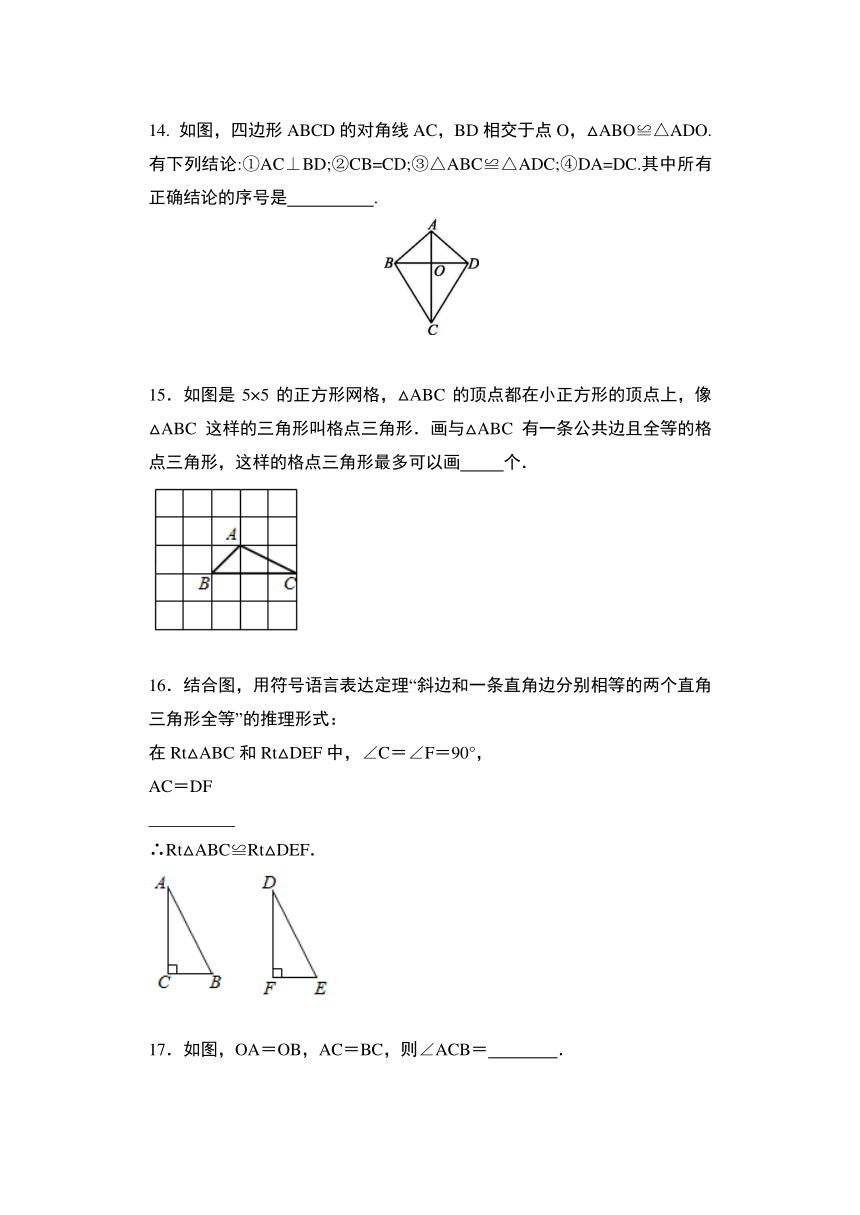
14.
如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是 .?
15.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画
个.
16.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
17.如图,OA=OB,AC=BC,则∠ACB=
.
18.如图,AD、BC表示两根长度相同的木条,若O是AD、BC的中点,则容器的内径CD为
cm.
三、解答题
19.
如图,在△ABE和△ACD中,给出以下四个论断:
(1)AB=AC;(2)AD=AE;
(3)AM=AN;(4)AD⊥DC,AE⊥BE.
请你以其中三个论断为题设,余下的一个论断为结论,使之组成一个真命题,并写出证明过程.
20.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
21.如图,AB=BC,∠BAD=∠BCD=90°,AE⊥EF于E,CF⊥EF于F,求证:Rt△ADE≌Rt△CDF.
22.如图,AB=AD,BC=CD
答案
一、选择题
1.
C
2.
C
3.
C
4.
C
5.
A
6.
C
7.
D
8.
C
9.
A
10.
B
二、填空题
11.
(4,0)或(4,4)或(0,4)
12.
∠B=∠E或∠C=∠D或AB=AE.
13.
3
14.
①②③
15.
6
16.
AB=DE
17.
60°
18.
9
三、解答题
19.
解:若要组成真命题,则论断(4)必须作为条件.因此可组成以下三个真命题:
命题①:若(1)(2)(4),则(3);命题②:若(1)(3)(4),则(2);命题③:若(2)(3)(4),则(1).
下面以命题①为例进行证明:
∵AD⊥DC,AE⊥BE,∴∠D=∠E=90°.
在Rt△ABE和Rt△ACD中,
∴Rt△ABE≌Rt△ACD(HL).
∴∠BAE=∠CAD.
∴∠BAE-∠BAC=∠CAD-∠BAC,
即∠EAN=∠DAM.
在△ADM和△AEN中,
∴△ADM≌△AEN(ASA).
∴AM=AN.
20.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
21.
解:连接BD,
∵∠BAD=∠BCD=90°,
在Rt△ABD和Rt△CBD中,
,
∴Rt△ABD≌Rt△CBD(HL),
∴AD=CD,
∵AE⊥EF于E,CF⊥EF于F,
∴∠E=∠F=90°,
在Rt△ADE和Rt△CDF中,
,
∴Rt△ADE≌Rt△CDF(HL).
22.
证明:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
又∵AD=AB,
∴BO=DO.
试卷第8页,总8页
三角形全等的判定暑期练习
一、选择题
1.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是(
)
A.△ADC≌△BCD
B.△ABD≌△BAC
C.△AOB≌△COD
D.△AOD≌△BOC
2.如图,在△ABC中,∠B=40°,AF=CD,AE=CF( )
A.50°
B.60°
C.70°
D.80°
3.
如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是
( )
4.如图,△ABC和△DEF中,AB=DE,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF
B.∠A=∠D
C.AC=DF
D.AC∥DF
5.
如图,小强画了一个与已知△ABC全等的△DEF,他画图的步骤是:(1)画DE=AB;(2)在DE的同旁画∠HDE=∠A,∠GED=∠B,DH,EG相交于点F,小强画图的依据是( )
A.ASA
B.SAS
C.SSS
D.AAS
6.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A.①
B.②
C.③
D.④
7.如图,∠C=∠D=90°,添加下列条件:①AC=AD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.0
B.1
C.2
D.3
8.
如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
9.如图,已知△ABC的六个元素,则下面甲、乙、丙、丁四个三角形中一定和△ABC全等的图形是( )
A.甲、丁
B.甲、丙
C.乙、丙
D.乙
10.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了( )
A.SSS
B.SAS
C.ASA
D.AAS
二、填空题
11.
在平面直角坐标系xOy中,已知点A,B的坐标分别为(2,0),(2,4),若以A,B,P为顶点的三角形与△ABO全等,则点P的坐标为________________________.
12.如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件是
.(只需写出一个条件即可)
13.如图,已知线段AB与CD相交于点E,AC=AD,则图中全等三角形有
对.
14.
如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是 .?
15.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画
个.
16.结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
AC=DF
∴Rt△ABC≌Rt△DEF.
17.如图,OA=OB,AC=BC,则∠ACB=
.
18.如图,AD、BC表示两根长度相同的木条,若O是AD、BC的中点,则容器的内径CD为
cm.
三、解答题
19.
如图,在△ABE和△ACD中,给出以下四个论断:
(1)AB=AC;(2)AD=AE;
(3)AM=AN;(4)AD⊥DC,AE⊥BE.
请你以其中三个论断为题设,余下的一个论断为结论,使之组成一个真命题,并写出证明过程.
20.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.
(1)求证:AE=AF;
(2)求∠EAF的度数.
21.如图,AB=BC,∠BAD=∠BCD=90°,AE⊥EF于E,CF⊥EF于F,求证:Rt△ADE≌Rt△CDF.
22.如图,AB=AD,BC=CD
答案
一、选择题
1.
C
2.
C
3.
C
4.
C
5.
A
6.
C
7.
D
8.
C
9.
A
10.
B
二、填空题
11.
(4,0)或(4,4)或(0,4)
12.
∠B=∠E或∠C=∠D或AB=AE.
13.
3
14.
①②③
15.
6
16.
AB=DE
17.
60°
18.
9
三、解答题
19.
解:若要组成真命题,则论断(4)必须作为条件.因此可组成以下三个真命题:
命题①:若(1)(2)(4),则(3);命题②:若(1)(3)(4),则(2);命题③:若(2)(3)(4),则(1).
下面以命题①为例进行证明:
∵AD⊥DC,AE⊥BE,∴∠D=∠E=90°.
在Rt△ABE和Rt△ACD中,
∴Rt△ABE≌Rt△ACD(HL).
∴∠BAE=∠CAD.
∴∠BAE-∠BAC=∠CAD-∠BAC,
即∠EAN=∠DAM.
在△ADM和△AEN中,
∴△ADM≌△AEN(ASA).
∴AM=AN.
20.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠CAD+∠ACD=∠CAD+∠EBA=90°,
∴∠ACD=∠EBA,
在△AEB和△FAC中,
,
∴△AEB≌△FAC(SAS),
∴AE=FA;
(2)解:∵△AEB≌△FAC,
∴∠E=∠CAF,
∵∠E+∠EAG=90°,
∴∠CAF+∠EAG=90°,
即∠EAF=90°.
21.
解:连接BD,
∵∠BAD=∠BCD=90°,
在Rt△ABD和Rt△CBD中,
,
∴Rt△ABD≌Rt△CBD(HL),
∴AD=CD,
∵AE⊥EF于E,CF⊥EF于F,
∴∠E=∠F=90°,
在Rt△ADE和Rt△CDF中,
,
∴Rt△ADE≌Rt△CDF(HL).
22.
证明:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
又∵AD=AB,
∴BO=DO.
试卷第8页,总8页
