基本不等式(陈艳)
图片预览




文档简介
(共16张PPT)
授课教师:
安庆一中 陈艳
(第一课时)
今有一台天平,两臂长不等,其余均精确. 有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次称量的结果的和的一半就是物体的真实重量,这种说法对吗?如果不对,是比真实重量重还是轻?
生活中的数学问题
ICM 2002
Beijing
August 20-28, 2002
International Congress of Mathemacticians
问题1:这个图案里有哪些我们学过的几何图形?
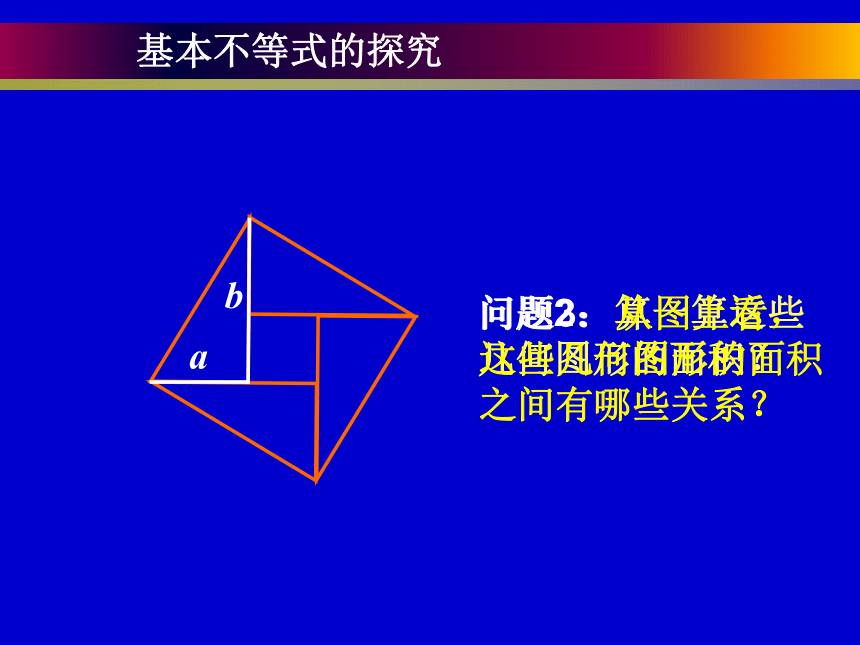
基本不等式的探究
b
a
问题2:算一算这些几何图形的面积?
问题3:从图上看,这些几何图形的面积之间有哪些关系?
基本不等式的探究
b
a
b
a
b
a
b
a
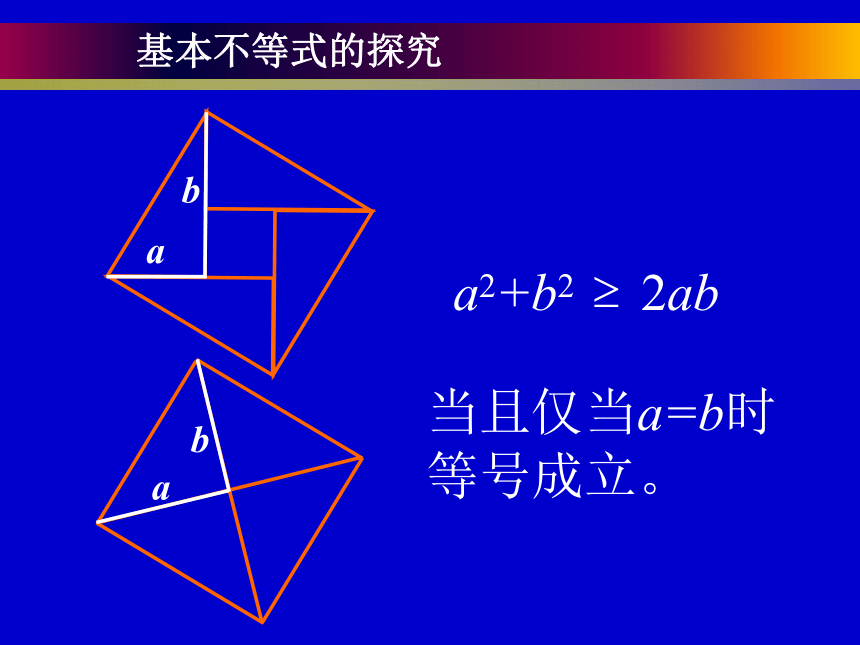
基本不等式的探究
b
a
b
a
当且仅当a=b时等号成立。
a2+b2 2ab
基本不等式的探究
(当且仅当a=b时,取“=”号)
若a,b∈R+,那么
a2+b2≥2ab
问题4:如果a,b∈R,那么以上的不等式是否仍然成立呢?
(当且仅当a=b时,取“=”号)
若a,b∈R,那么
a2+b2≥2ab
基本不等式的探究
基本不等式:
若a>0,b>0,
a2+b2≥2ab (当且仅当a=b时,取“=”号)
(当且仅当a=b时,取“=”号)
换b
换a
(当且仅当a=b时,取“=”号)
其中, 称为正数 的算术平均数, 称为它们的几何平均数.
基本不等式的探究
基本不等式的几何意义
A
B
C
D
O
.
a
b
E
.
半径不小于半弦
(当且仅当a=b时,取“=”号)
基本不等式
今有一台天平,两臂长不等,其余均精确. 有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次称量的结果的和的一半就是物体的真实重量,这种说法对吗?如果不对,是比真实重量重还是轻?
l1
l2
G
a
b
G
问题解决
基本不等式的初步应用
基本不等式的初步应用
课堂小结
这两个不等式都是重要的不等式,有着广泛的应用价值。
我们从形和数多角度共同探究了基本不等式
应用这两个不等式时一定要注意等号成立的条件,以及a、b的取值范围。
(当且仅当a=b时,取“=”号)
(当且仅当a=b时,
取“=”号)
1. P1OO 练习1
2.思考题:现有甲、乙两商场对单价相同的同类商品进行促销,甲商场采取的促销方式是在原价p折的基础上再打q折,乙商场的促销方式则是在原价 折的基础上再打 折,请问对顾客而言,哪种打折方式更合算?
作 业
授课教师:
安庆一中 陈艳
(第一课时)
今有一台天平,两臂长不等,其余均精确. 有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次称量的结果的和的一半就是物体的真实重量,这种说法对吗?如果不对,是比真实重量重还是轻?
生活中的数学问题
ICM 2002
Beijing
August 20-28, 2002
International Congress of Mathemacticians
问题1:这个图案里有哪些我们学过的几何图形?
基本不等式的探究
b
a
问题2:算一算这些几何图形的面积?
问题3:从图上看,这些几何图形的面积之间有哪些关系?
基本不等式的探究
b
a
b
a
b
a
b
a
基本不等式的探究
b
a
b
a
当且仅当a=b时等号成立。
a2+b2 2ab
基本不等式的探究
(当且仅当a=b时,取“=”号)
若a,b∈R+,那么
a2+b2≥2ab
问题4:如果a,b∈R,那么以上的不等式是否仍然成立呢?
(当且仅当a=b时,取“=”号)
若a,b∈R,那么
a2+b2≥2ab
基本不等式的探究
基本不等式:
若a>0,b>0,
a2+b2≥2ab (当且仅当a=b时,取“=”号)
(当且仅当a=b时,取“=”号)
换b
换a
(当且仅当a=b时,取“=”号)
其中, 称为正数 的算术平均数, 称为它们的几何平均数.
基本不等式的探究
基本不等式的几何意义
A
B
C
D
O
.
a
b
E
.
半径不小于半弦
(当且仅当a=b时,取“=”号)
基本不等式
今有一台天平,两臂长不等,其余均精确. 有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次称量的结果的和的一半就是物体的真实重量,这种说法对吗?如果不对,是比真实重量重还是轻?
l1
l2
G
a
b
G
问题解决
基本不等式的初步应用
基本不等式的初步应用
课堂小结
这两个不等式都是重要的不等式,有着广泛的应用价值。
我们从形和数多角度共同探究了基本不等式
应用这两个不等式时一定要注意等号成立的条件,以及a、b的取值范围。
(当且仅当a=b时,取“=”号)
(当且仅当a=b时,
取“=”号)
1. P1OO 练习1
2.思考题:现有甲、乙两商场对单价相同的同类商品进行促销,甲商场采取的促销方式是在原价p折的基础上再打q折,乙商场的促销方式则是在原价 折的基础上再打 折,请问对顾客而言,哪种打折方式更合算?
作 业
