抛物线的几何性质
图片预览

文档简介
(共15张PPT)
(第一课时)
授课教师:
安庆一中 陈艳
温故知新
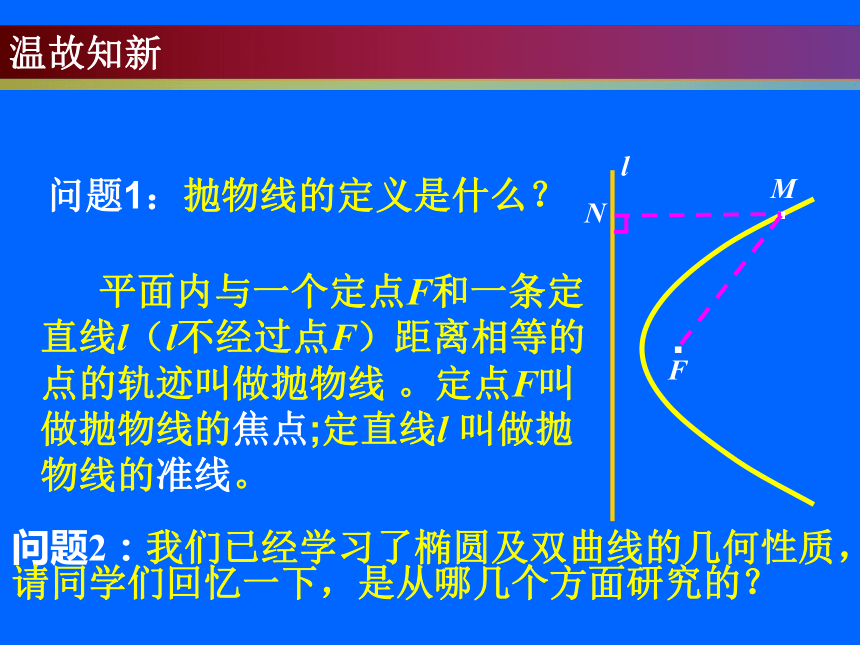
问题1:抛物线的定义是什么?
平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线 。定点F叫做抛物线的焦点;定直线l 叫做抛物线的准线。
.
F
l
M
.
N
问题2:我们已经学习了椭圆及双曲线的几何性质,请同学们回忆一下,是从哪几个方面研究的?
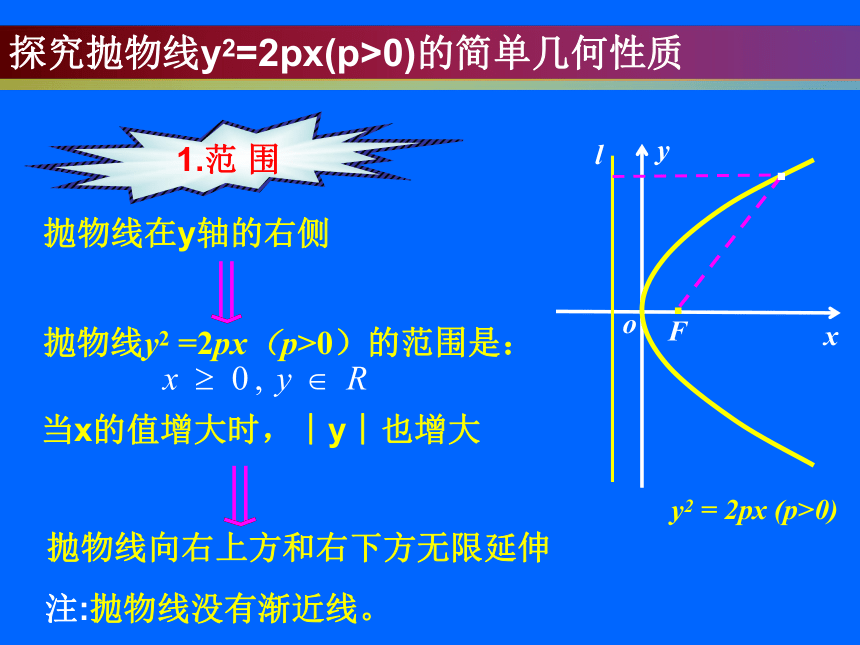
探究抛物线y2=2px(p>0)的简单几何性质
1.范 围
抛物线在y轴的右侧
抛物线y2 =2px(p>0)的范围是:
当x的值增大时,︱y︱也增大
抛物线向右上方和右下方无限延伸
注:抛物线没有渐近线。
y2 = 2px (p>0)
.
x
o
y
F
l
.
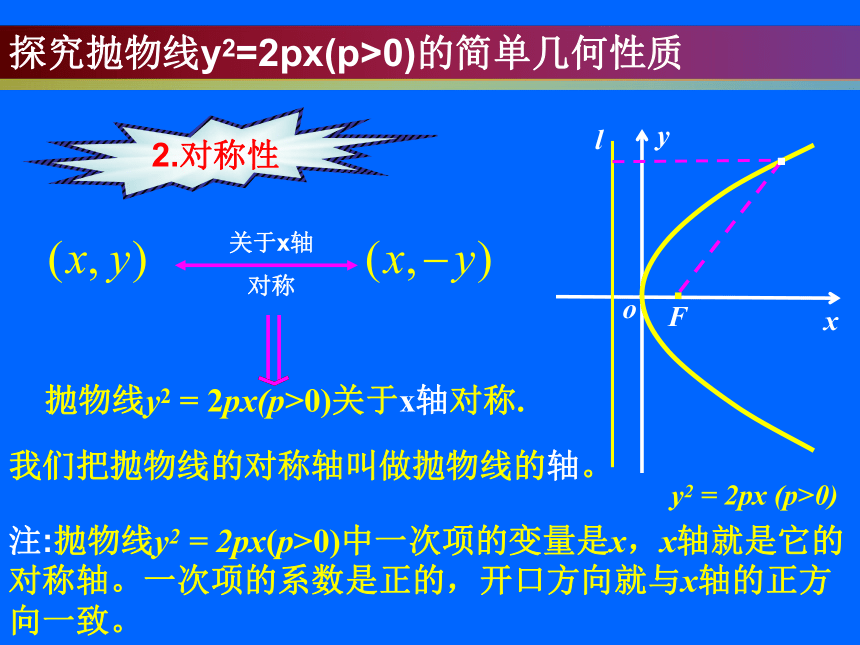
探究抛物线y2=2px(p>0)的简单几何性质
2.对称性
抛物线y2 = 2px(p>0)关于x轴对称.
关于x轴
对称
注:抛物线y2 = 2px(p>0)中一次项的变量是x,x轴就是它的对称轴。一次项的系数是正的,开口方向就与x轴的正方向一致。
我们把抛物线的对称轴叫做抛物线的轴。
y2 = 2px (p>0)
.
x
o
y
F
l
.
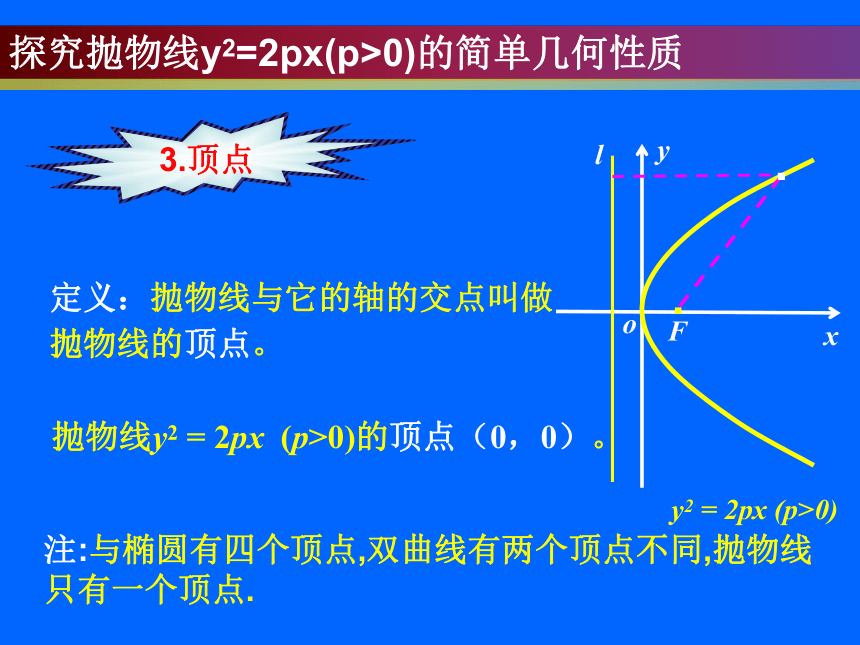
探究抛物线y2=2px(p>0)的简单几何性质
3.顶点
注:与椭圆有四个顶点,双曲线有两个顶点不同,抛物线只有一个顶点.
定义:抛物线与它的轴的交点叫做抛物线的顶点。
抛物线y2 = 2px (p>0)的顶点(0,0)。
y2 = 2px (p>0)
.
x
o
y
F
l
.
探究抛物线y2=2px(p>0)的简单几何性质
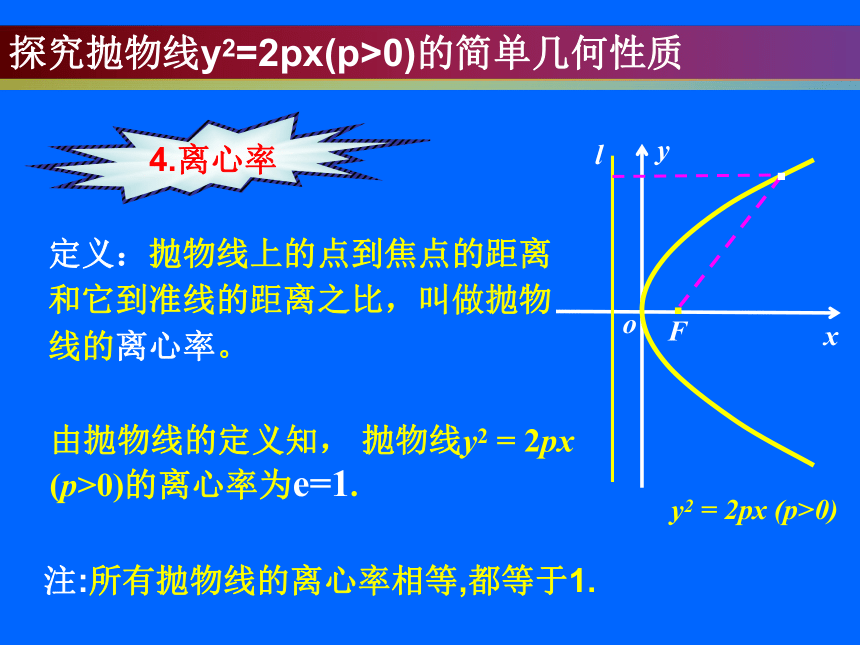
4.离心率
注:所有抛物线的离心率相等,都等于1.
定义:抛物线上的点到焦点的距离和它到准线的距离之比,叫做抛物线的离心率。
由抛物线的定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.
y2 = 2px (p>0)
.
x
o
y
F
l
.
探究抛物线y2=2px(p>0)的简单几何性质
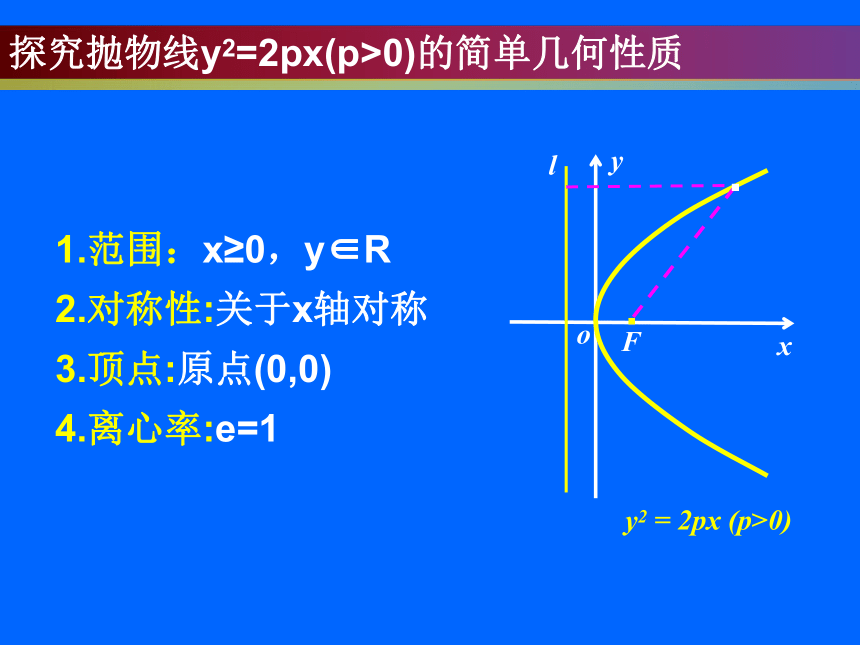
1.范围:x≥0,y∈R
2.对称性:关于x轴对称
3.顶点:原点(0,0)
4.离心率:e=1
y2 = 2px (p>0)
.
x
o
y
F
l
.
归纳四种形式的抛物线的简单几何性质
方程
图
形
范围
对称性
顶点
离心率
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
l
F
y
x
O
关于x轴对称
(0,0)
x≤0
y∈R
关于x轴对称
x∈R
y≥0
关于y轴对称
y≤0
x∈R
关于y轴对称
e=1
例1.已知抛物线关于 轴对称,它的顶点在坐标原点,并且经过点 ,求它的标准方程.
则将M点代入得: 2 = 2p×2 解得:p=2
因此所求抛物线的标准方程为:y2=4x
解:由已知可设抛物线的标准方程为y2=2px(p>0)
思考: 顶点在坐标原点,对称轴是坐标轴,并且经过
点 的抛物线有几条 求出它们的标准方程 。
抛物线的简单几何性质的应用
抛物线的简单几何性质的应用
A
.
x
O
y
F
B
(x1,y1)
(x2,y2)
(1,0)
y=x-1
l
在抛物线y2 = 2x上求一点P, 使P到焦点F与到点A ( 3,2 )的距离之和最小.
学以致用
P
Q
l
A
x
y
O
F
E
P0
抛物线的简单几何性质的应用
思考:观察它们开口的大小,并说明抛物线开口大小与什么有关?
练习:在同一坐标系中画出下列抛物线:
问题1:在同一坐标系中画出下列抛物线:
x
O
y
x0
p越大,抛物线开口越大.
课堂小结
类比椭圆、双曲线的几何性质,结合抛物线的图形和标准方程,研究了抛物线的简单几何性质。
利用抛物线的这些性质,解决了抛物线的有关问题。
在解决问题的过程中,我们深刻体会到利用曲线的几何特征常常能简化计算,使得解析几何问题迎刃而解。
再次应用并掌握了解析几何中的重要方法——待定系数法。
作业
1. P73 习题2.4 A组5,6
2. 请结合P62《探究与发现》“为什么
是双曲线 的渐近线?” 探究:为什
么抛物线没有渐近线?
(第一课时)
授课教师:
安庆一中 陈艳
温故知新
问题1:抛物线的定义是什么?
平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线 。定点F叫做抛物线的焦点;定直线l 叫做抛物线的准线。
.
F
l
M
.
N
问题2:我们已经学习了椭圆及双曲线的几何性质,请同学们回忆一下,是从哪几个方面研究的?
探究抛物线y2=2px(p>0)的简单几何性质
1.范 围
抛物线在y轴的右侧
抛物线y2 =2px(p>0)的范围是:
当x的值增大时,︱y︱也增大
抛物线向右上方和右下方无限延伸
注:抛物线没有渐近线。
y2 = 2px (p>0)
.
x
o
y
F
l
.
探究抛物线y2=2px(p>0)的简单几何性质
2.对称性
抛物线y2 = 2px(p>0)关于x轴对称.
关于x轴
对称
注:抛物线y2 = 2px(p>0)中一次项的变量是x,x轴就是它的对称轴。一次项的系数是正的,开口方向就与x轴的正方向一致。
我们把抛物线的对称轴叫做抛物线的轴。
y2 = 2px (p>0)
.
x
o
y
F
l
.
探究抛物线y2=2px(p>0)的简单几何性质
3.顶点
注:与椭圆有四个顶点,双曲线有两个顶点不同,抛物线只有一个顶点.
定义:抛物线与它的轴的交点叫做抛物线的顶点。
抛物线y2 = 2px (p>0)的顶点(0,0)。
y2 = 2px (p>0)
.
x
o
y
F
l
.
探究抛物线y2=2px(p>0)的简单几何性质
4.离心率
注:所有抛物线的离心率相等,都等于1.
定义:抛物线上的点到焦点的距离和它到准线的距离之比,叫做抛物线的离心率。
由抛物线的定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.
y2 = 2px (p>0)
.
x
o
y
F
l
.
探究抛物线y2=2px(p>0)的简单几何性质
1.范围:x≥0,y∈R
2.对称性:关于x轴对称
3.顶点:原点(0,0)
4.离心率:e=1
y2 = 2px (p>0)
.
x
o
y
F
l
.
归纳四种形式的抛物线的简单几何性质
方程
图
形
范围
对称性
顶点
离心率
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
l
F
y
x
O
关于x轴对称
(0,0)
x≤0
y∈R
关于x轴对称
x∈R
y≥0
关于y轴对称
y≤0
x∈R
关于y轴对称
e=1
例1.已知抛物线关于 轴对称,它的顶点在坐标原点,并且经过点 ,求它的标准方程.
则将M点代入得: 2 = 2p×2 解得:p=2
因此所求抛物线的标准方程为:y2=4x
解:由已知可设抛物线的标准方程为y2=2px(p>0)
思考: 顶点在坐标原点,对称轴是坐标轴,并且经过
点 的抛物线有几条 求出它们的标准方程 。
抛物线的简单几何性质的应用
抛物线的简单几何性质的应用
A
.
x
O
y
F
B
(x1,y1)
(x2,y2)
(1,0)
y=x-1
l
在抛物线y2 = 2x上求一点P, 使P到焦点F与到点A ( 3,2 )的距离之和最小.
学以致用
P
Q
l
A
x
y
O
F
E
P0
抛物线的简单几何性质的应用
思考:观察它们开口的大小,并说明抛物线开口大小与什么有关?
练习:在同一坐标系中画出下列抛物线:
问题1:在同一坐标系中画出下列抛物线:
x
O
y
x0
p越大,抛物线开口越大.
课堂小结
类比椭圆、双曲线的几何性质,结合抛物线的图形和标准方程,研究了抛物线的简单几何性质。
利用抛物线的这些性质,解决了抛物线的有关问题。
在解决问题的过程中,我们深刻体会到利用曲线的几何特征常常能简化计算,使得解析几何问题迎刃而解。
再次应用并掌握了解析几何中的重要方法——待定系数法。
作业
1. P73 习题2.4 A组5,6
2. 请结合P62《探究与发现》“为什么
是双曲线 的渐近线?” 探究:为什
么抛物线没有渐近线?
