双曲线几何性质
图片预览


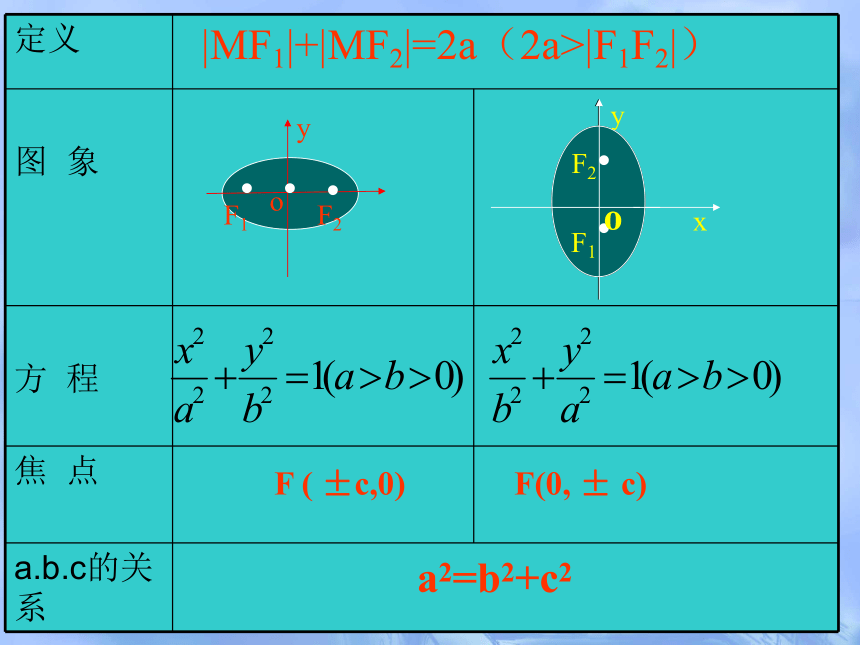





文档简介
(共25张PPT)
济宁高新区高级中学 熊德忠
1、椭圆定义是什么?
2、椭圆的标准方程是什么?
复习引入
定义
图 象
方 程
焦 点
a.b.c的关系
y
o
x
F1
F2
·
·
y
o
F1
F2
·
·
|MF1|+|MF2|=2a(2a>|F1F2|)
a2=b2+c2
F ( ±c,0) F(0, ± c)
o
F1
F2
·
·
·
o
平面内与两个定点F1,F2的距离的差的绝对值等于常数2a(小于| F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点
两焦点之间的距离2c叫做双曲线的焦距
F1
F2
M
形成概念
1、定义中为什么要强调“平面内”?
2、定义中为什么要强调“差的绝对值”?
3、说说定义中常数2a的取值范围?
深化认识
相关结论:
例1:指出下列方程所表示的曲线
1、
2、
3、
4、
典例讲评
总结:
单双看绝对值,类型看2a与2c
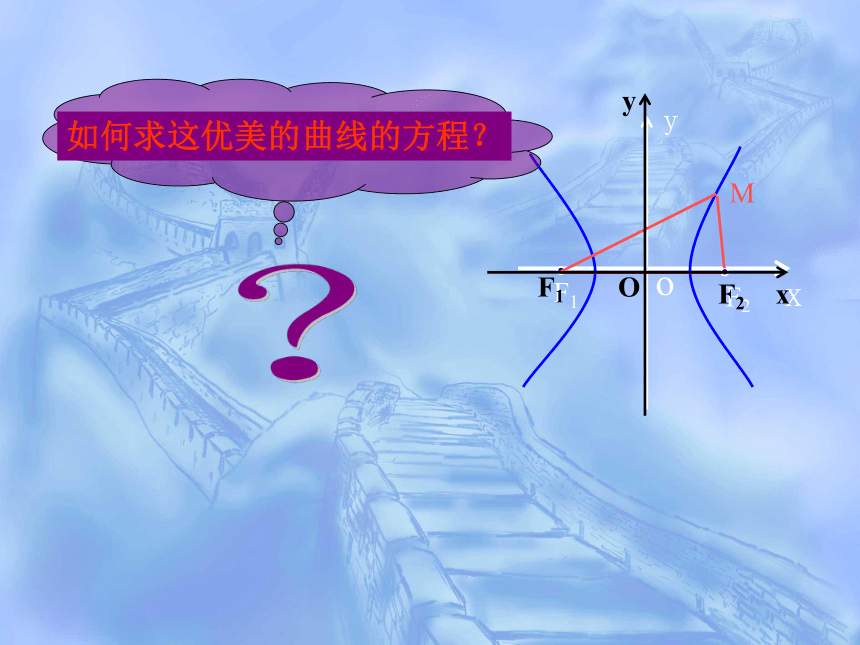
x
y
o
F1
F2
M
如何求这优美的曲线的方程?
F1
F2
x
O
y
焦点在y轴上的双曲线的标准方程
想一想
F2
F1
y
x
o
F1(0,-c), F2(0,c)
,
焦点在y轴上的双曲线的图象
是什么?标准方程怎样求?
与椭圆比较:
1.焦点位置椭圆看大小,双曲线看正负,与a、b大小无关,a〉0,b〉0。
2.椭圆a最大,双曲线c最大。
注:
例题 判断下列曲线焦点的位置
例题 关于标准方程
例1已知双曲线两个焦点的坐标为F1( - 5 , 0)、F2(5 , 0),双曲线上一点P到F1、F2的距离的差
的绝对值等于6,求双曲线的标准方程。
解:因为双曲线的焦点在x轴上,所以设它的
∵ 2a=6 2c=10
∴ a=3 c=5
∴ b2= 52- 32= 16
∴ 所求双曲线的标准方程为
标准方程为
(2)双曲线的一个焦点坐标为(0,-6),经过点
A(-5,6)
例2 若方程 表示的曲线
是双曲线,求k的取值范围.
例3:
若椭圆 与双曲线
的焦点相同,则 a =
3
例4. 相距2000m的两个哨所A、B,听到远处传来的炮弹的爆炸声。已知当时的声速是330m/s,在A哨所听到爆炸声的时间比在B哨所听到时迟4s,试判断爆炸点在什么样的曲线上,并求出曲线的方程。
解(1)设爆炸点P,由已知可得
|PA|—|PB|=330 4=1320
因为|AB|=2000>1320,又|PA|>|PB|,所以点P在以A、B为焦点的双曲线的靠近B处的那支上。
(2)如图2—17,建立直角坐标系xOy,使 A、B两点在x轴上,并且点O与线段AB的中点重合.
设爆炸点P的坐标为(x,y),则
即2a=1320,a=660.2c=2000,c=1000
b2=c2-a2=564400
所求双曲线的方程为:
课堂练习:
1、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足
|PF1| - |PF2|= 10,则P点的轨迹是( )
A、双曲线 B、双曲线一支
C、直线 D、一条射线
D
变式1:已知双曲线的焦点为F1(0, -5),
F2(0, 5),双曲线上一点P到F1、F2的距
离的差的绝对值等于6,求双曲线的
标准方程;
变式练习
变式2:已知双曲线的焦距为10,双曲线
上一点P到F1、F2的距离的差的绝对值
等于6,求双曲线的标准方程;
变式练习
变式3:已知双曲线的焦点为F1( -5 , 0 ),
F2( 5 , 0 ),双曲线上一点P的坐标
为 ,求双曲线的标准方程.
变式练习
变式4:
已知双曲线的焦点在x轴上,且经过点 (3, 0)、 (0, 4), ,求曲线的标准方程;
变式练习
课堂小结:
1双曲线的定义
单双看绝对值,类型看2a与2c
2标准方程
与椭圆比较:
焦点位置椭圆看大小,双曲线看正负;
椭圆a最大,双曲线c最大。
作业:
必做:教材 P55练习1-3
选做:练习册
济宁高新区高级中学 熊德忠
1、椭圆定义是什么?
2、椭圆的标准方程是什么?
复习引入
定义
图 象
方 程
焦 点
a.b.c的关系
y
o
x
F1
F2
·
·
y
o
F1
F2
·
·
|MF1|+|MF2|=2a(2a>|F1F2|)
a2=b2+c2
F ( ±c,0) F(0, ± c)
o
F1
F2
·
·
·
o
平面内与两个定点F1,F2的距离的差的绝对值等于常数2a(小于| F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点
两焦点之间的距离2c叫做双曲线的焦距
F1
F2
M
形成概念
1、定义中为什么要强调“平面内”?
2、定义中为什么要强调“差的绝对值”?
3、说说定义中常数2a的取值范围?
深化认识
相关结论:
例1:指出下列方程所表示的曲线
1、
2、
3、
4、
典例讲评
总结:
单双看绝对值,类型看2a与2c
x
y
o
F1
F2
M
如何求这优美的曲线的方程?
F1
F2
x
O
y
焦点在y轴上的双曲线的标准方程
想一想
F2
F1
y
x
o
F1(0,-c), F2(0,c)
,
焦点在y轴上的双曲线的图象
是什么?标准方程怎样求?
与椭圆比较:
1.焦点位置椭圆看大小,双曲线看正负,与a、b大小无关,a〉0,b〉0。
2.椭圆a最大,双曲线c最大。
注:
例题 判断下列曲线焦点的位置
例题 关于标准方程
例1已知双曲线两个焦点的坐标为F1( - 5 , 0)、F2(5 , 0),双曲线上一点P到F1、F2的距离的差
的绝对值等于6,求双曲线的标准方程。
解:因为双曲线的焦点在x轴上,所以设它的
∵ 2a=6 2c=10
∴ a=3 c=5
∴ b2= 52- 32= 16
∴ 所求双曲线的标准方程为
标准方程为
(2)双曲线的一个焦点坐标为(0,-6),经过点
A(-5,6)
例2 若方程 表示的曲线
是双曲线,求k的取值范围.
例3:
若椭圆 与双曲线
的焦点相同,则 a =
3
例4. 相距2000m的两个哨所A、B,听到远处传来的炮弹的爆炸声。已知当时的声速是330m/s,在A哨所听到爆炸声的时间比在B哨所听到时迟4s,试判断爆炸点在什么样的曲线上,并求出曲线的方程。
解(1)设爆炸点P,由已知可得
|PA|—|PB|=330 4=1320
因为|AB|=2000>1320,又|PA|>|PB|,所以点P在以A、B为焦点的双曲线的靠近B处的那支上。
(2)如图2—17,建立直角坐标系xOy,使 A、B两点在x轴上,并且点O与线段AB的中点重合.
设爆炸点P的坐标为(x,y),则
即2a=1320,a=660.2c=2000,c=1000
b2=c2-a2=564400
所求双曲线的方程为:
课堂练习:
1、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足
|PF1| - |PF2|= 10,则P点的轨迹是( )
A、双曲线 B、双曲线一支
C、直线 D、一条射线
D
变式1:已知双曲线的焦点为F1(0, -5),
F2(0, 5),双曲线上一点P到F1、F2的距
离的差的绝对值等于6,求双曲线的
标准方程;
变式练习
变式2:已知双曲线的焦距为10,双曲线
上一点P到F1、F2的距离的差的绝对值
等于6,求双曲线的标准方程;
变式练习
变式3:已知双曲线的焦点为F1( -5 , 0 ),
F2( 5 , 0 ),双曲线上一点P的坐标
为 ,求双曲线的标准方程.
变式练习
变式4:
已知双曲线的焦点在x轴上,且经过点 (3, 0)、 (0, 4), ,求曲线的标准方程;
变式练习
课堂小结:
1双曲线的定义
单双看绝对值,类型看2a与2c
2标准方程
与椭圆比较:
焦点位置椭圆看大小,双曲线看正负;
椭圆a最大,双曲线c最大。
作业:
必做:教材 P55练习1-3
选做:练习册
