安徽省六安市舒城县2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 安徽省六安市舒城县2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 22:10:31 | ||
图片预览




文档简介
舒城县2020-2021学年度第二学期期末质检
高一数学试卷
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若复数z满足false,则false( )
A.1 B.2 C. false D.false
2.从6个篮球、2个排球中任选3个球,则下列事件中,是必然事件的是( )
A.3个都是篮球 B.至少有1个是排球
C.3个都是排球 D.至少有1个是篮球
3.已知在平行四边形ABCD中,点M、N分别是BC、CD的中点,如果false,那么向量false( )
A.false B.false C.false D.false
4.某学校对甲、乙两个班级的某次成绩进行统计分析,制成了如图的条形图与扇形图,则下列说法一定正确的是( )
A.甲班不及格率高于乙班不及格率 B.甲班平均成绩高于乙班平均成绩
C.甲班学生比乙班学生发挥稳定 D.甲班成绩优良人数超过了乙班成绩优良人数
5.口袋中有100个大小相同的红球、白球、黑球,其中红球32个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为( )
A.0.32 B.0.45 C.0.64 D.0.67
6.已知圆锥的表面积为3false,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A.false B.false C.false D.false
7.设m,n是两条不同直线,false,false是两个不同平面,则下列说法错误的是( )
A.若m⊥false,n⊥false,则m//n; B.若false//false,m⊥false,则m⊥false;
C.若m//false,n//false,则m//n; D.若m⊥false,m//false,则false⊥false.
8.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位舒城县居民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的80%分位数是( )
A.7.5 B.8 C.8.5 D.9
9.若(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,那么△ABC是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
10.如图,在正方形ABCD中,AB=2,E为BC的中点,点P是以AB为直径的圆弧上任一点.则false的最大值为( )
A.4 B.5 C.false D.2+false
11.【市示范选做】连掷一枚均匀的骰子两次,所得向上的点数分别为m,n,记t=m+n,当t=4时的概率是( )
A.false B.false C.false D.false
11.【省示范选做】连掷一枚均匀的骰子两次,所得向上的点数分别为m,n,记t=m+n,则下列说法正确的是( )
A.事件“t=12”的概率为false B.事件“t是奇数”与“m=n”互为对立事件
C.事件“t=2”与“t≠3”互为互斥事件 D.事件“t>8且mn<32”的概率为false
12.【市示范选做】如图,正方体false的棱长为1,则下列四个命题错误的是( )
A.若点M,N分别是线段false的中点,则false
B.点C到平面false的距离为false
C.直线BC与平面false所成的角等于false
D.三棱柱false的外接球的表面积为3false
12.【省示范选做】如图,ABCD是边长为2的正方形,点E,F分别为边BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,则下列结论错误的是( )
A.AP⊥EF
B.点P在平面AEF内的射影为△AEF的垂心
C.二面角A-EF-P的余弦值为false
D.若四面体P-AEF的四个顶点在同一个球面上,则该球的表面积是24false
二、填空题(本题共4小题,每小题5分,共20分)
13.天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
488 932 812 458 989 431 257 390 024 556
734 113 537 569 683 907 966 191 925 271
据此估计,这三天中恰有两天下雨的概率近似为 .
14.已知false,向量false与向量false的夹角为false,则向量false在向量false方向上的投影向量的坐标为 .
15.【市示范选做】一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当a>b,b<c时称为“凹数”(如213),若false,且a,b,c互不相同,则这个三位数为“凹数”的概率为 .
15.【省示范选做】一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当a>b,b<c时称为“凹数”如213),若false,且a,b,c互不相同,则这个三位数为“凹数”的概率为 .
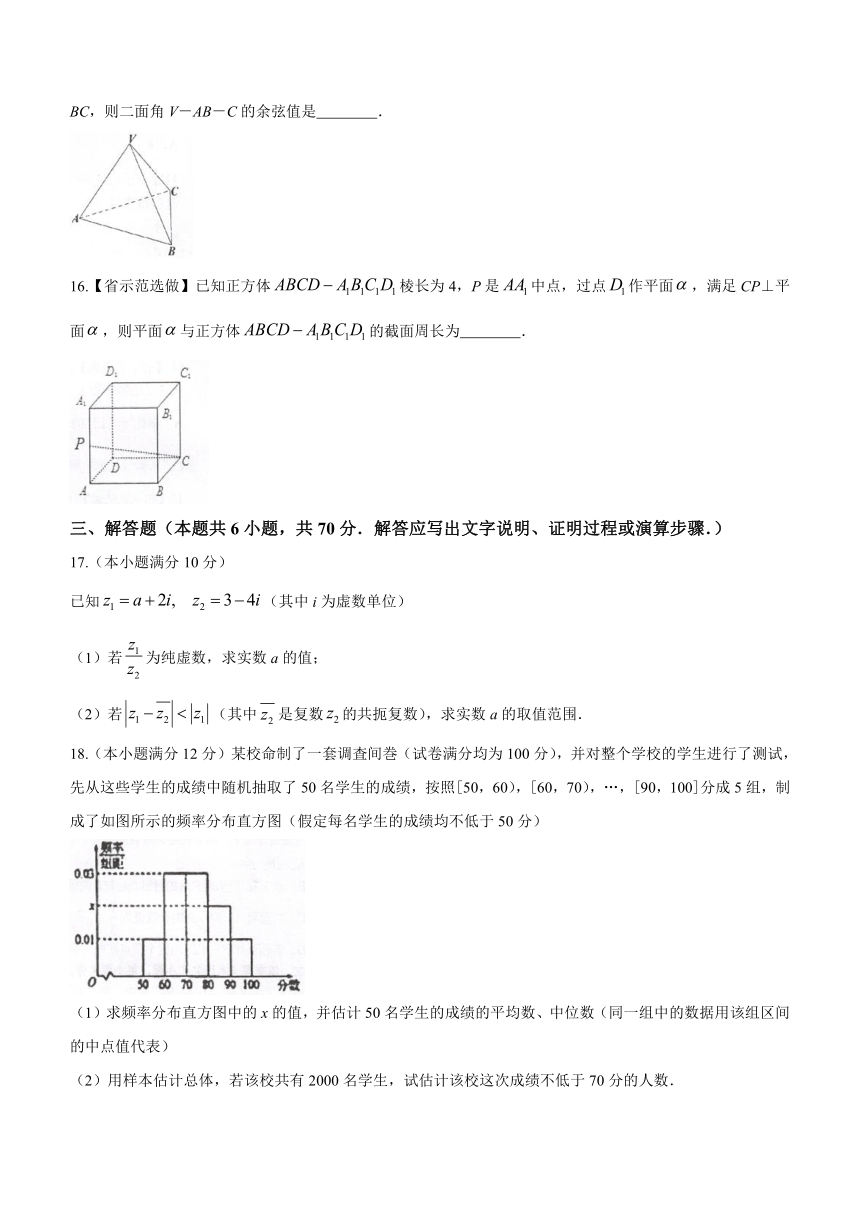
16.【市示范选做】如图,在三棱锥V-ABC中,AB=false,VA=VB,AC=BC,VC=1,且AV⊥BV,AC⊥BC,则二面角V-AB-C的余弦值是 .
16.【省示范选做】已知正方体false棱长为4,P是false中点,过点false作平面false,满足CP⊥平面false,则平面false与正方体false的截面周长为 .
三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知false(其中i为虚数单位)
(1)若false为纯虚数,求实数a的值;
(2)若false(其中false是复数false的共扼复数),求实数a的取值范围.
18.(本小题满分12分)某校命制了一套调査间巻(试卷满分均为100分),并对整个学校的学生进行了测试,先从这些学生的成绩中随机抽取了50名学生的成绩,按照[50,60),[60,70),…,[90,100]分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)
(1)求频率分布直方图中的x的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)
(2)用样本估计总体,若该校共有2000名学生,试估计该校这次成绩不低于70分的人数.
19.(本小题满分12分)如图,在平面直角坐标系xOy中,false.
(1)求点B,点C的坐标;
(2)求四边形OABC的面积.
20.(本小题满分12分)如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3
(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;
(2)求证:PA⊥平面PCD.
21.【市示范选做】(本小题满分12分)
甲、乙两射击运动员分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)两人都射中的概率;
(2)两人中至少有一人射中的概率.
21.【省示范选做】(本小题满分12分)进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土地资源的消耗,具有社会、经济、生态等多方面的效益,是关乎生态文明建设全局的大事.为了普及垃圾分类知识,某学校举行了垃圾分类知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为p,乙同学答对每题的概率都为q(p>q),且在考试中每人各题答题结果互不影响.已知每题甲,乙同时答对的概率为false,恰有一人答对的概率为false.
(1)求p和q的值;
(2)试求两人共答对3道题的概率.
22.【市示范选做】(本小题满分12分)
某社区规划在小区内建立一个如图所示的圆形休闲区,经调研确定,该圆内接四边形ABCD为儿童娛乐设施建筑用地,AB=AD=2CD=6,BC=9
(1)求儿童娱乐设施建筑用地的面积;
(2)若A,C,D不动,在圆弧false上取一点E,使得儿童娱乐设施的新建筑用地AECD的面积最大,并求出最大值.
22.【省示范选做】(本小题满分12分)
如图所示,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M,N在线段DE(含端点)上,且点M在点N的右下方,经测量得知,AD=6m,AE=6m,AP=2m,∠MPN=false.记∠EPM=false(rad),监控摄像头的可视区域△PMN的面积为Sfalse.
(1)求S关于false的函数关系式,并写出false的取值范围;(参考数据:false)
(2)求S的最小值.
参考答案
一、选择题
题
号
1
2
3
4
5
6
7
8
9
10
11市
11
省
12
市
12
省
答案
D
D
B
A
B
A
C
C
B
D
B
D
B
D
二、填空题
0.3 ; 14、false ; 15市、false ;
15省、false ; 16市、 false ; 16省、4false+6false.
三、解答题
17、【解析】(1)由false,false,
得false,------3分
falsefalse为纯虚数,falsefalse,且false,falsefalse.-------5分
(2)false,-------6分
falsefalse,falsefalse,即false,------8分
解得false.-------10分
18、(1)由频率分布直方图得,第4组的频率为为1﹣(0.01+0.03+0.03+0.01)×10=0.2,
所以x=0.02; - ------2分
所以抽到50名学生成绩的平均数为
false=(55×0.01+65×0.03+75×0.03+85×0.02+95×0.01)×10=74;
由于前两组的频率之和为0.1+0.3=0.4, -------5分
前三组的频率之和为0.1+0.3+0.3=0.7,所以中位数在第3组;
设中位数为t分,则有(t﹣70)×0.03=0.1,解得t=false;所以所求中位数是false.-------8分
(2)由(1)知50学生中不低于70分的的频率为0.3+0.2+0.1=0.6,
用样本估计总体,估计高三年级2000名学生中成绩不低于70分的人数为
2000×0.6=1200(人). -------12分
19、【解析】(1)在平面直角坐标系xOy中,设false,则
因为false,所以A(2,0). ---------2分
又false.所以false,false
所以点false. --------4分
又 false,所以false,
所以点false --------6分
由(1)可得false,false,-------8分
所以false 又false,所以四边形OABC为等腰梯形,-------10分
如图,延长CB交x轴于点D,则DC= DO,BD=AD.
又false,则false,false均为等边三角形.
∴四边形false的面积false--------12分
20、【解析】(1)证明:连接false,易知false,false.
又由false,故false.
又因为false平面false,false平面false,所以false平面false; --------6分
(2)证明:如图,取棱false的中点false,连接false. 依题意得false,
又因为平面false平面false,平面false平面false,false平面false,
所以false平面false,
又false平面false,故false.
又已知false,false,所以false平面false; -------12分
【市示范选做】
设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B.事件A与B是相互独立的.
(1)两人都射中的概率为P(AB)=P(A)P(B)=0.8×0.9=0.72. -------5分
(2)两人中至少有一人射中的概率等于1减去两个人都没有击中的概率,
∴所求的概率等于 1﹣P(false)=1﹣P(false)?P(false)=1﹣0.2×0.1=0.98. -------12分
21、【省示范选做】
【详解】(1)设false{甲同学答对第一题},false{乙同学答对第一题},则false,false.
设false{甲、乙二人均答对第一题},false{甲、乙二人中恰有一人答对第一题},
则false,false.
由于二人答题互不影响,且每人各题答题结果互不影响,所以false与false相互独立,false与false相互互斥,所以false,false
false.
由题意可得false
即false解得false或false
由于false,所以false,false.
(2)设false{甲同学答对了false道题},false{乙同学答对了false道题},false,1,2.
由题意得,false,false,
false,false.
设false{甲乙二人共答对3道题},则false.
由于false和false相互独立,false与false相互互斥,
所以false.
所以,甲乙二人共答对3道题的概率为false.
22、【市示范选做】
.【解析】(1)连接AC(图略),由题意可得false ,
则false.①
由余弦定理可得
false,
则false.②
由①②可得false,从而false.
故四边形ABCD的面积为
falsefalse.
(2)由余弦定理可得false.
由(1)可得false,
由余弦定理可得false,则false,
从而△AEC的面积false.
由(1)可知△ACD的面积为false ,
则儿童娱乐设施的新建筑用地AECD的面积为false.
22、【省示范选做】
【解析】(1)解法1:在false中,false,false,false,false,由正弦定理得false,
所以false. ------2分
同理,在false中,由正弦定理得false,
所以false. -------4分
所以false的面积
falsefalsefalse
falsefalse,
当false与false重合时,false;
当false与false重合时,false,即false,false,所以false.
综上,可得false,false.--------6分
解法2:在false中,false,false,false,false,由正弦定理可知,false,
所以false. -------2分
在false中,由正弦定理可知false,
所以false. ---------4分
所以false.
又点false到false的距离为false,
所以false的面积
falsefalsefalsefalse
false,
当false与false重合时,false;当false与false重合时,false,
即false,false,所以false.
综上,可得false,false. -------6分
(2)false -------8分
当false,即false时,false -------10分
false取得最小值为false.
所以可视区域false面积的最小值为false. ------12分
高一数学试卷
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若复数z满足false,则false( )
A.1 B.2 C. false D.false
2.从6个篮球、2个排球中任选3个球,则下列事件中,是必然事件的是( )
A.3个都是篮球 B.至少有1个是排球
C.3个都是排球 D.至少有1个是篮球
3.已知在平行四边形ABCD中,点M、N分别是BC、CD的中点,如果false,那么向量false( )
A.false B.false C.false D.false
4.某学校对甲、乙两个班级的某次成绩进行统计分析,制成了如图的条形图与扇形图,则下列说法一定正确的是( )
A.甲班不及格率高于乙班不及格率 B.甲班平均成绩高于乙班平均成绩
C.甲班学生比乙班学生发挥稳定 D.甲班成绩优良人数超过了乙班成绩优良人数
5.口袋中有100个大小相同的红球、白球、黑球,其中红球32个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为( )
A.0.32 B.0.45 C.0.64 D.0.67
6.已知圆锥的表面积为3false,它的侧面展开图是一个半圆,则此圆锥的体积为( )
A.false B.false C.false D.false
7.设m,n是两条不同直线,false,false是两个不同平面,则下列说法错误的是( )
A.若m⊥false,n⊥false,则m//n; B.若false//false,m⊥false,则m⊥false;
C.若m//false,n//false,则m//n; D.若m⊥false,m//false,则false⊥false.
8.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位舒城县居民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的80%分位数是( )
A.7.5 B.8 C.8.5 D.9
9.若(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,那么△ABC是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
10.如图,在正方形ABCD中,AB=2,E为BC的中点,点P是以AB为直径的圆弧上任一点.则false的最大值为( )
A.4 B.5 C.false D.2+false
11.【市示范选做】连掷一枚均匀的骰子两次,所得向上的点数分别为m,n,记t=m+n,当t=4时的概率是( )
A.false B.false C.false D.false
11.【省示范选做】连掷一枚均匀的骰子两次,所得向上的点数分别为m,n,记t=m+n,则下列说法正确的是( )
A.事件“t=12”的概率为false B.事件“t是奇数”与“m=n”互为对立事件
C.事件“t=2”与“t≠3”互为互斥事件 D.事件“t>8且mn<32”的概率为false
12.【市示范选做】如图,正方体false的棱长为1,则下列四个命题错误的是( )
A.若点M,N分别是线段false的中点,则false
B.点C到平面false的距离为false
C.直线BC与平面false所成的角等于false
D.三棱柱false的外接球的表面积为3false
12.【省示范选做】如图,ABCD是边长为2的正方形,点E,F分别为边BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,则下列结论错误的是( )
A.AP⊥EF
B.点P在平面AEF内的射影为△AEF的垂心
C.二面角A-EF-P的余弦值为false
D.若四面体P-AEF的四个顶点在同一个球面上,则该球的表面积是24false
二、填空题(本题共4小题,每小题5分,共20分)
13.天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
488 932 812 458 989 431 257 390 024 556
734 113 537 569 683 907 966 191 925 271
据此估计,这三天中恰有两天下雨的概率近似为 .
14.已知false,向量false与向量false的夹角为false,则向量false在向量false方向上的投影向量的坐标为 .
15.【市示范选做】一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当a>b,b<c时称为“凹数”(如213),若false,且a,b,c互不相同,则这个三位数为“凹数”的概率为 .
15.【省示范选做】一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当a>b,b<c时称为“凹数”如213),若false,且a,b,c互不相同,则这个三位数为“凹数”的概率为 .
16.【市示范选做】如图,在三棱锥V-ABC中,AB=false,VA=VB,AC=BC,VC=1,且AV⊥BV,AC⊥BC,则二面角V-AB-C的余弦值是 .
16.【省示范选做】已知正方体false棱长为4,P是false中点,过点false作平面false,满足CP⊥平面false,则平面false与正方体false的截面周长为 .
三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知false(其中i为虚数单位)
(1)若false为纯虚数,求实数a的值;
(2)若false(其中false是复数false的共扼复数),求实数a的取值范围.
18.(本小题满分12分)某校命制了一套调査间巻(试卷满分均为100分),并对整个学校的学生进行了测试,先从这些学生的成绩中随机抽取了50名学生的成绩,按照[50,60),[60,70),…,[90,100]分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)
(1)求频率分布直方图中的x的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)
(2)用样本估计总体,若该校共有2000名学生,试估计该校这次成绩不低于70分的人数.
19.(本小题满分12分)如图,在平面直角坐标系xOy中,false.
(1)求点B,点C的坐标;
(2)求四边形OABC的面积.
20.(本小题满分12分)如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3
(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;
(2)求证:PA⊥平面PCD.
21.【市示范选做】(本小题满分12分)
甲、乙两射击运动员分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)两人都射中的概率;
(2)两人中至少有一人射中的概率.
21.【省示范选做】(本小题满分12分)进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土地资源的消耗,具有社会、经济、生态等多方面的效益,是关乎生态文明建设全局的大事.为了普及垃圾分类知识,某学校举行了垃圾分类知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为p,乙同学答对每题的概率都为q(p>q),且在考试中每人各题答题结果互不影响.已知每题甲,乙同时答对的概率为false,恰有一人答对的概率为false.
(1)求p和q的值;
(2)试求两人共答对3道题的概率.
22.【市示范选做】(本小题满分12分)
某社区规划在小区内建立一个如图所示的圆形休闲区,经调研确定,该圆内接四边形ABCD为儿童娛乐设施建筑用地,AB=AD=2CD=6,BC=9
(1)求儿童娱乐设施建筑用地的面积;
(2)若A,C,D不动,在圆弧false上取一点E,使得儿童娱乐设施的新建筑用地AECD的面积最大,并求出最大值.
22.【省示范选做】(本小题满分12分)
如图所示,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M,N在线段DE(含端点)上,且点M在点N的右下方,经测量得知,AD=6m,AE=6m,AP=2m,∠MPN=false.记∠EPM=false(rad),监控摄像头的可视区域△PMN的面积为Sfalse.
(1)求S关于false的函数关系式,并写出false的取值范围;(参考数据:false)
(2)求S的最小值.
参考答案
一、选择题
题
号
1
2
3
4
5
6
7
8
9
10
11市
11
省
12
市
12
省
答案
D
D
B
A
B
A
C
C
B
D
B
D
B
D
二、填空题
0.3 ; 14、false ; 15市、false ;
15省、false ; 16市、 false ; 16省、4false+6false.
三、解答题
17、【解析】(1)由false,false,
得false,------3分
falsefalse为纯虚数,falsefalse,且false,falsefalse.-------5分
(2)false,-------6分
falsefalse,falsefalse,即false,------8分
解得false.-------10分
18、(1)由频率分布直方图得,第4组的频率为为1﹣(0.01+0.03+0.03+0.01)×10=0.2,
所以x=0.02; - ------2分
所以抽到50名学生成绩的平均数为
false=(55×0.01+65×0.03+75×0.03+85×0.02+95×0.01)×10=74;
由于前两组的频率之和为0.1+0.3=0.4, -------5分
前三组的频率之和为0.1+0.3+0.3=0.7,所以中位数在第3组;
设中位数为t分,则有(t﹣70)×0.03=0.1,解得t=false;所以所求中位数是false.-------8分
(2)由(1)知50学生中不低于70分的的频率为0.3+0.2+0.1=0.6,
用样本估计总体,估计高三年级2000名学生中成绩不低于70分的人数为
2000×0.6=1200(人). -------12分
19、【解析】(1)在平面直角坐标系xOy中,设false,则
因为false,所以A(2,0). ---------2分
又false.所以false,false
所以点false. --------4分
又 false,所以false,
所以点false --------6分
由(1)可得false,false,-------8分
所以false 又false,所以四边形OABC为等腰梯形,-------10分
如图,延长CB交x轴于点D,则DC= DO,BD=AD.
又false,则false,false均为等边三角形.
∴四边形false的面积false--------12分
20、【解析】(1)证明:连接false,易知false,false.
又由false,故false.
又因为false平面false,false平面false,所以false平面false; --------6分
(2)证明:如图,取棱false的中点false,连接false. 依题意得false,
又因为平面false平面false,平面false平面false,false平面false,
所以false平面false,
又false平面false,故false.
又已知false,false,所以false平面false; -------12分
【市示范选做】
设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B.事件A与B是相互独立的.
(1)两人都射中的概率为P(AB)=P(A)P(B)=0.8×0.9=0.72. -------5分
(2)两人中至少有一人射中的概率等于1减去两个人都没有击中的概率,
∴所求的概率等于 1﹣P(false)=1﹣P(false)?P(false)=1﹣0.2×0.1=0.98. -------12分
21、【省示范选做】
【详解】(1)设false{甲同学答对第一题},false{乙同学答对第一题},则false,false.
设false{甲、乙二人均答对第一题},false{甲、乙二人中恰有一人答对第一题},
则false,false.
由于二人答题互不影响,且每人各题答题结果互不影响,所以false与false相互独立,false与false相互互斥,所以false,false
false.
由题意可得false
即false解得false或false
由于false,所以false,false.
(2)设false{甲同学答对了false道题},false{乙同学答对了false道题},false,1,2.
由题意得,false,false,
false,false.
设false{甲乙二人共答对3道题},则false.
由于false和false相互独立,false与false相互互斥,
所以false.
所以,甲乙二人共答对3道题的概率为false.
22、【市示范选做】
.【解析】(1)连接AC(图略),由题意可得false ,
则false.①
由余弦定理可得
false,
则false.②
由①②可得false,从而false.
故四边形ABCD的面积为
falsefalse.
(2)由余弦定理可得false.
由(1)可得false,
由余弦定理可得false,则false,
从而△AEC的面积false.
由(1)可知△ACD的面积为false ,
则儿童娱乐设施的新建筑用地AECD的面积为false.
22、【省示范选做】
【解析】(1)解法1:在false中,false,false,false,false,由正弦定理得false,
所以false. ------2分
同理,在false中,由正弦定理得false,
所以false. -------4分
所以false的面积
falsefalsefalse
falsefalse,
当false与false重合时,false;
当false与false重合时,false,即false,false,所以false.
综上,可得false,false.--------6分
解法2:在false中,false,false,false,false,由正弦定理可知,false,
所以false. -------2分
在false中,由正弦定理可知false,
所以false. ---------4分
所以false.
又点false到false的距离为false,
所以false的面积
falsefalsefalsefalse
false,
当false与false重合时,false;当false与false重合时,false,
即false,false,所以false.
综上,可得false,false. -------6分
(2)false -------8分
当false,即false时,false -------10分
false取得最小值为false.
所以可视区域false面积的最小值为false. ------12分
同课章节目录
