江苏省张家港市后塍高中11-12学年高一下学期5月综合练习数学试题
文档属性
| 名称 | 江苏省张家港市后塍高中11-12学年高一下学期5月综合练习数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 166.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-12 19:14:15 | ||
图片预览


文档简介
江苏省张家港市后塍高中11-12学年高一下学期5月综合练习数学试题
2012.5
一、填空题:(每题5分,共70分)
1.函数的最小正周期为 ▲ .
2.是第四象限角,,则 ▲ .
3.下面是一个算法的伪代码.如果输入的值是2,
则输出的值是 ▲ .
4.某学校共有师生2400人,现用分层抽样的方法,从所有
师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的学生人数是 ▲ .
5.在100的水中有一个草履虫,现从中随机取出20水样放到显微镜下观察,则发现草履虫的概率是 ▲ .
6.右图是甲乙两名运动员某赛季一些场次得分的茎叶图,
则平均得分高的是 ▲ 运动员.
7.已知,,,则与夹角的
度数为 ▲ .
8.在平面直角坐标系中,正方形的对角线的两端点
分别为,,则 ▲ .
9.某同学五次考试的数学成绩分别是120, 129, 121,125,130,则这五次考试成绩
的方差是 ▲ .(方差公式:)
10.某种产品的广告费支出与销售额之间有如下对应数据:
∕元 2 4 5 6 8
y∕元 30 40 60 50 70
根据散点图分析,与具有线性相关关系,且线性回归方程为,
则的值为 ▲ .
11.已知两个正变量满足,则使不等式恒成立的实数的取值范围是 .
12.已知,则 ▲ .
13.如图,有以下命题:设点,是线段的
三等分点,则有,把此命题推
广,设点,,....,是的等
分点(),则有 ▲ .
14.2002年在北京召开的国际数学家大会,会标是以我国古代数学家
赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小
正方形拼成的一个大正方形(如图).如果小正方形的面积为1,
大正方形的面积为25,直角三角形中较大的锐角为,
那么的值等于 ▲ .
二、解答题:(解答时要有证明过程或必要的文字说明)
15.已知,与的夹角是.⑴求的值;⑵求的值.
16.已知,,且∥,
⑴求的值;⑵求的值.
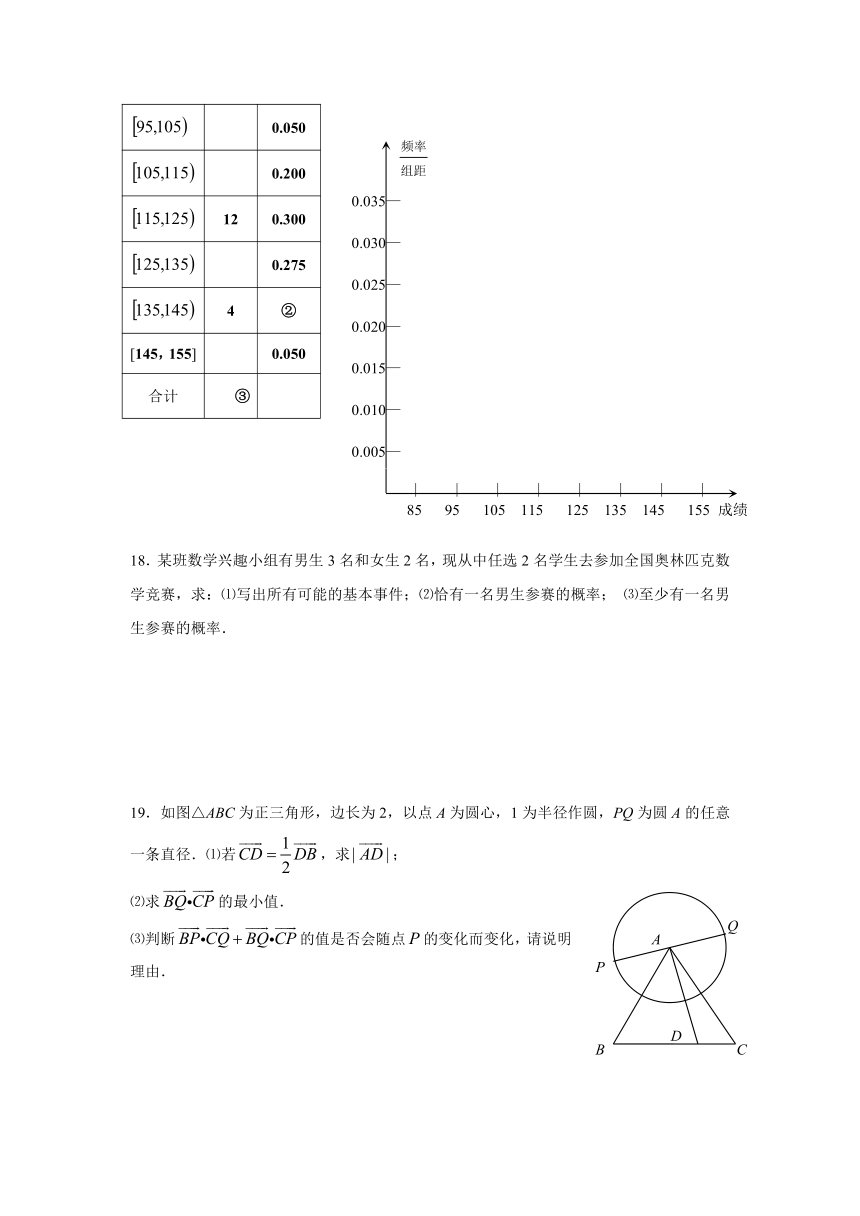
17.高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
⑴根据下面图表,①②③处的数值分别为 、 、 ;
⑵在所给的坐标系中画出[85,155]的频率分布直方图;
⑶根据题中信息估计总体平均数.
分组 频数 频率
① 0.025
0.050
0.200
12 0.300
0.275
4 ②
[145,155] 0.050
合计 ③
18.某班数学兴趣小组有男生3名和女生2名,现从中任选2名学生去参加全国奥林匹克数学竞赛,求:⑴写出所有可能的基本事件;⑵恰有一名男生参赛的概率; ⑶至少有一名男生参赛的概率.
19.如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.⑴若,求;
⑵求的最小值.
⑶判断的值是否会随点的变化而变化,请说明理由.
20.如图,直角三角形中,,,.点分别在边和上(点和点不重合),将△沿翻折,△变为△,使顶点落在边上(点和点不重合).设.
⑴用表示线段的长度,并写出的取值范围;
⑵在△中,若,
求线段长度的最小值.
高一数学参考答案
一、填空题:(每题5分,共70分)
1、 2、 3、20 4、2250 5、 6、甲 7、 8、1
9、16.4 10、17.5 11、 12、 13、 14、
二、解答题:(解答时要有证明过程或必要的文字说明)
15、解:⑴根据下面图表,①②③处的数值分别为1,0.100,40.
⑵在所给的坐标系中画出[85,155]的频率分布直方图;
⑶根据题中信息估计总体平均数.
利用组中值得平均数
=900.025+1000.05+1100.2+1200.3+1300.275+1400.1+1500.05=122.5
所以估计总体平均数为122.5.
16.解:,的夹角是
⑴
⑵
17.解:⑴
⑵原式
18.解:⑴记男生3名和女生2名分别为从中任选2名共有10种情况,
即为 ,,,,,
,,,,.
⑵记“恰有一名男生参赛”为事件,事件包含基本事件共有6个,即为,
,,,,.
所以.
⑶记“至少有一名男生参赛”为事件,事件包含基本事件共有9个,即为
,,,,,
,,,.
所以.
答:从中任选2名共有10种情况,恰有一名男生参赛的概率为,至少有一名男生参赛的概率为.
19.⑴,
,
⑵设,则
当时,即时,有最小值,
⑶的值不随点的变化而变化
由⑵知,,所以的值不随点的变化而变化.
20.解:(1)设,则.
在Rt△MB中,,
∴.
∵点M在线段AB上,M点和B点不重合,点和B点不重合,
∴.
(2),在△AMN中,
∠ANM=,,
=.
令
==.
∵, ∴.
当且仅当,时,有最大值,
∴时,有最小值.
Read x
If x≤5 Then
y←10x
Else
y←2.5x+5
End If
Print y
(第3题)
甲 乙
0 8
50 1 247
32 2 199
875421 3 36
944 4
1 5 2
(第6题)
O
A
P
Q
B
(第13题)
(第14题)
0.035—
0.005—
0.010—
0.015—
0.020—
0.025—
0.025—
0.030—
| | | | | | | |
85 95 105 115 125 135 145 155 成绩
A
C
B
Q
P
D
A'
A
C
N
M
B
0.035—
0.005—
0.010—
0.015—
0.020—
0.025—
0.025—
0.030—
| | | | | | | |
85 95 105 115 125 135 145 155 成绩
A'
C
N
M
A
B
2012.5
一、填空题:(每题5分,共70分)
1.函数的最小正周期为 ▲ .
2.是第四象限角,,则 ▲ .
3.下面是一个算法的伪代码.如果输入的值是2,
则输出的值是 ▲ .
4.某学校共有师生2400人,现用分层抽样的方法,从所有
师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的学生人数是 ▲ .
5.在100的水中有一个草履虫,现从中随机取出20水样放到显微镜下观察,则发现草履虫的概率是 ▲ .
6.右图是甲乙两名运动员某赛季一些场次得分的茎叶图,
则平均得分高的是 ▲ 运动员.
7.已知,,,则与夹角的
度数为 ▲ .
8.在平面直角坐标系中,正方形的对角线的两端点
分别为,,则 ▲ .
9.某同学五次考试的数学成绩分别是120, 129, 121,125,130,则这五次考试成绩
的方差是 ▲ .(方差公式:)
10.某种产品的广告费支出与销售额之间有如下对应数据:
∕元 2 4 5 6 8
y∕元 30 40 60 50 70
根据散点图分析,与具有线性相关关系,且线性回归方程为,
则的值为 ▲ .
11.已知两个正变量满足,则使不等式恒成立的实数的取值范围是 .
12.已知,则 ▲ .
13.如图,有以下命题:设点,是线段的
三等分点,则有,把此命题推
广,设点,,....,是的等
分点(),则有 ▲ .
14.2002年在北京召开的国际数学家大会,会标是以我国古代数学家
赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小
正方形拼成的一个大正方形(如图).如果小正方形的面积为1,
大正方形的面积为25,直角三角形中较大的锐角为,
那么的值等于 ▲ .
二、解答题:(解答时要有证明过程或必要的文字说明)
15.已知,与的夹角是.⑴求的值;⑵求的值.
16.已知,,且∥,
⑴求的值;⑵求的值.
17.高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
⑴根据下面图表,①②③处的数值分别为 、 、 ;
⑵在所给的坐标系中画出[85,155]的频率分布直方图;
⑶根据题中信息估计总体平均数.
分组 频数 频率
① 0.025
0.050
0.200
12 0.300
0.275
4 ②
[145,155] 0.050
合计 ③
18.某班数学兴趣小组有男生3名和女生2名,现从中任选2名学生去参加全国奥林匹克数学竞赛,求:⑴写出所有可能的基本事件;⑵恰有一名男生参赛的概率; ⑶至少有一名男生参赛的概率.
19.如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.⑴若,求;
⑵求的最小值.
⑶判断的值是否会随点的变化而变化,请说明理由.
20.如图,直角三角形中,,,.点分别在边和上(点和点不重合),将△沿翻折,△变为△,使顶点落在边上(点和点不重合).设.
⑴用表示线段的长度,并写出的取值范围;
⑵在△中,若,
求线段长度的最小值.
高一数学参考答案
一、填空题:(每题5分,共70分)
1、 2、 3、20 4、2250 5、 6、甲 7、 8、1
9、16.4 10、17.5 11、 12、 13、 14、
二、解答题:(解答时要有证明过程或必要的文字说明)
15、解:⑴根据下面图表,①②③处的数值分别为1,0.100,40.
⑵在所给的坐标系中画出[85,155]的频率分布直方图;
⑶根据题中信息估计总体平均数.
利用组中值得平均数
=900.025+1000.05+1100.2+1200.3+1300.275+1400.1+1500.05=122.5
所以估计总体平均数为122.5.
16.解:,的夹角是
⑴
⑵
17.解:⑴
⑵原式
18.解:⑴记男生3名和女生2名分别为从中任选2名共有10种情况,
即为 ,,,,,
,,,,.
⑵记“恰有一名男生参赛”为事件,事件包含基本事件共有6个,即为,
,,,,.
所以.
⑶记“至少有一名男生参赛”为事件,事件包含基本事件共有9个,即为
,,,,,
,,,.
所以.
答:从中任选2名共有10种情况,恰有一名男生参赛的概率为,至少有一名男生参赛的概率为.
19.⑴,
,
⑵设,则
当时,即时,有最小值,
⑶的值不随点的变化而变化
由⑵知,,所以的值不随点的变化而变化.
20.解:(1)设,则.
在Rt△MB中,,
∴.
∵点M在线段AB上,M点和B点不重合,点和B点不重合,
∴.
(2),在△AMN中,
∠ANM=,,
=.
令
==.
∵, ∴.
当且仅当,时,有最大值,
∴时,有最小值.
Read x
If x≤5 Then
y←10x
Else
y←2.5x+5
End If
Print y
(第3题)
甲 乙
0 8
50 1 247
32 2 199
875421 3 36
944 4
1 5 2
(第6题)
O
A
P
Q
B
(第13题)
(第14题)
0.035—
0.005—
0.010—
0.015—
0.020—
0.025—
0.025—
0.030—
| | | | | | | |
85 95 105 115 125 135 145 155 成绩
A
C
B
Q
P
D
A'
A
C
N
M
B
0.035—
0.005—
0.010—
0.015—
0.020—
0.025—
0.025—
0.030—
| | | | | | | |
85 95 105 115 125 135 145 155 成绩
A'
C
N
M
A
B
同课章节目录
