江苏省徐州七中11-12学年高一下学期第十四周学情调研数学试题
文档属性
| 名称 | 江苏省徐州七中11-12学年高一下学期第十四周学情调研数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 190.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-12 19:13:38 | ||
图片预览


文档简介
江苏省徐州七中11-12学年高一下学期第十四周学情调研数学试题
一.填空题(本大题共18小题,每小题5分,共90分)
1. 下列赋值语句中正确的是________.
①x←3; ②3←x;
③x-3←0; ④3-x←0.
解析:赋值语句一般是把值赋给左边的变量,只是一个字母,故只有①正确.
2.以下伪代码执行后,变量a,b的值分别为________.
a←15b←20a←a+bb←a-ba←a-bPrint a,b
解析:a的初始值为15,第3步a的值为35,第4步b的值为15,第5步a=35-15=20,故输出a=20,b=15.
3. 该伪代码运行后,输出的值y为________.
x←3If x>3 Then y←x×xElse y←2×xEnd IfPrint y
解析:y=∵x=3,∴y=6.
4.阅读下面的伪代码:
Read xIf x>1 Theny←x2+1Else y←2x+1End IfPrint y
若执行上述伪代码时没有执行y←x2+1,则输入的x的取值范围是________.
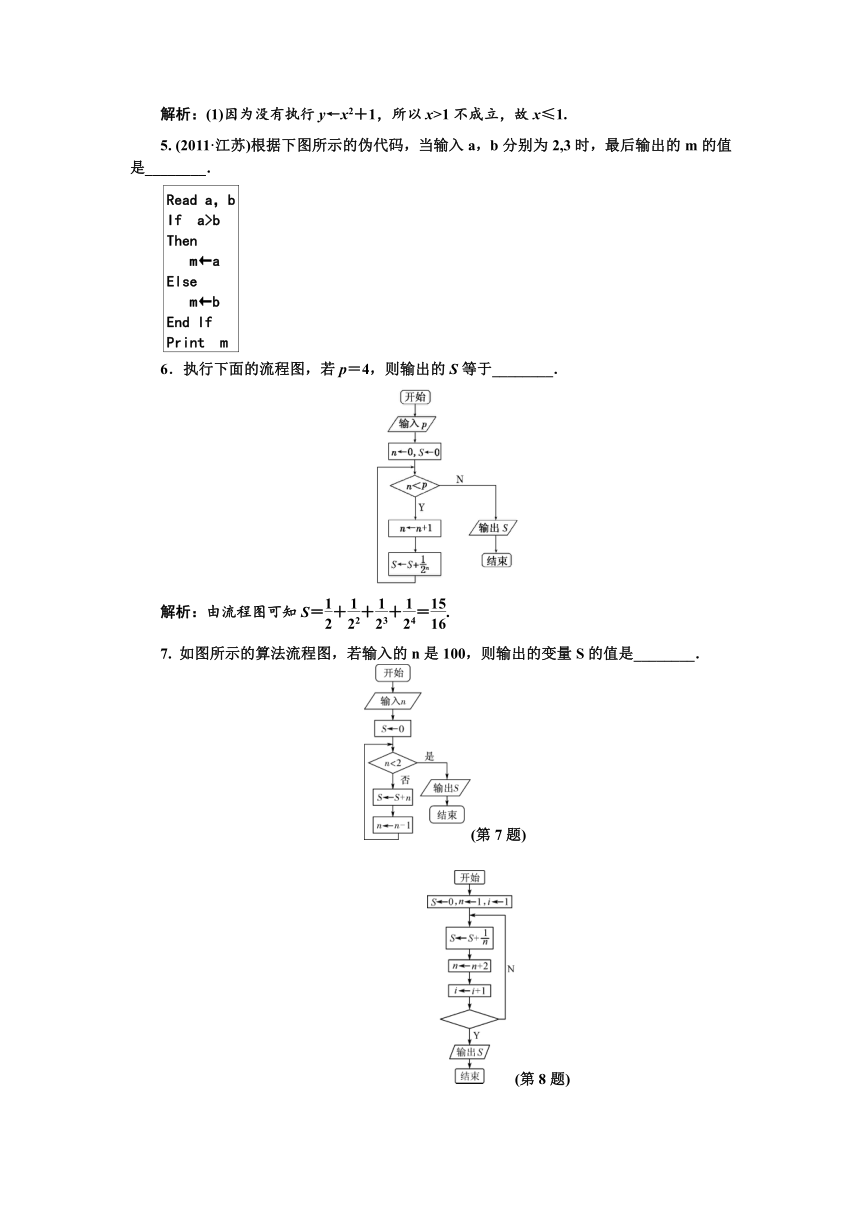
解析:(1)因为没有执行y←x2+1,所以x>1不成立,故x≤1.
5. (2011·江苏)根据下图所示的伪代码,当输入a,b分别为2,3时,最后输出的m的值是________.
6.执行下面的流程图,若p=4,则输出的S等于________.
解析:由流程图可知S=+++=.
7. 如图所示的算法流程图,若输入的n是100,则输出的变量S的值是________.
(第7题)
(第8题)
8. 如图给出的是计算1+++…+的值的一个程序框图,其中判断框内应填入的条件是i>________.
9. 阅读下面的伪代码:
若要使这个算法执行的结果是计算1+2+3+…+1000,则S的初始值x=________.
答案:0
10. 已知伪代码如下,则输出结果S=________.
I←0S←0While I<6 I←I+2 S←S+I 2End WhilePrint S
解析:根据伪代码可知:第一次循环:I=2,S=22=4;第二次循环:I=4,S=4+42=20;第三次循环:I=6,S=20+62=56;因I=6,所以循环结束,S=56.
11.下列伪代码执行后输出的结果是________.
解析:该程序的功能是计算S=5+4+…+n到首次不小于14的n-1的值,可得n=1.
12.写出表示下列伪代码运算功能的算术表达式________.
解析:用“追踪”法:S=,i=2→S=+,i=3,…,S=++…+,i=10.
答案:S=++…+
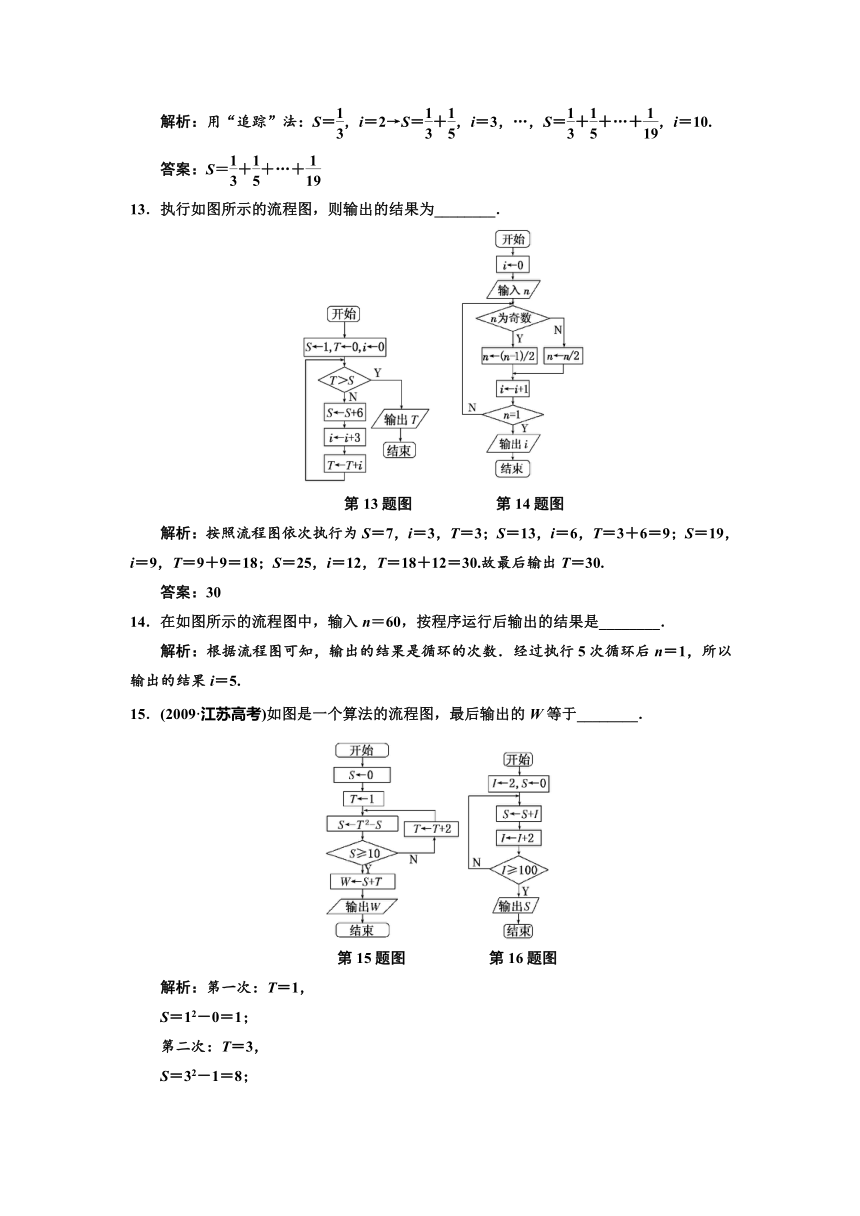
13.执行如图所示的流程图,则输出的结果为________.
第13题图 第14题图
解析:按照流程图依次执行为S=7,i=3,T=3;S=13,i=6,T=3+6=9;S=19,i=9,T=9+9=18;S=25,i=12,T=18+12=30.故最后输出T=30.
答案:30
14.在如图所示的流程图中,输入n=60,按程序运行后输出的结果是________.
解析:根据流程图可知,输出的结果是循环的次数.经过执行5次循环后n=1,所以输出的结果i=5.
15.(2009·江苏高考)如图是一个算法的流程图,最后输出的W等于________.
第15题图 第16题图
解析:第一次:T=1,
S=12-0=1;
第二次:T=3,
S=32-1=8;
第三次:T=5,
S=52-8=17.
此时满足S≥10.
所以W=S+T=17+5=22.
答案:22
16.如图所示流程图中,循环体执行的次数是________.
解析:从流程图反映的算法是S=2+4+6+8+…,I的初始值为2,由I=I+2知,执行了49次时,I=100,满足I≥100,退出循环.答案:49
17.下图是一个算法的流程图,则输出S的值是 ▲ .
18.执行如图所示的流程图,则输出的结果是________.
解析:如果把i<2010时的各个a值记作数列{an},那么这个程序第1次运行计算的是a2=,第2次运行计算的是a3=,…,第n次运行计算的是an+1=,故这个程序的功能是计算数列{an}的第2010项的值.将an+1=变形为=+1,故数列{}是首项为1,公差为1的等差数列,故=n,即an=,故输出结果是.
二.解答题(本大题共3小题,共30分)
19.如图,在边长为4的正方形ABCD的边上有一点P,它沿折线BCDA由B向A运动,设运动路程为x,△APB的面积为y,
(1)求y关于x的函数解析式,并指出其定义域.
(2)用伪代码写出根据输入的x的值计算y值的一个算法.
20.甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的流程图分别如图1和图2.
(1)根据图1和图2,当n=20时分别求出它们输出的结果;试判断甲、乙两位同学编写的流程图输出的结果是否一致?
(2)若希望通过对图2虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的流程图.
图1 图2
解:(1)图1中程序的功能是求2+4+6+8+…+2n的和,当n=20时,S=2+4+6+…+40=420.
图2中程序的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.
所以甲、乙两位同学编写的程序输出的结果是一致的.
(2)修改后部分流程图为:
21.已知数列{an}的各项均为正数,观察程序框图,当k=4时, ,当k=9时,
(1)试求数列{an}的通项;
(2)令bn=2nan,求b1+b2+…+bn的值.
(1)由框图知:
∵{an}为等差数列,设公差为d,
(2)设Tn=b1+b2+…+bn
=2×1+22×4+23×7+…+(3n-2)×2n
则2Tn=22×1+23×4+24×7+…+2n+1×(3n-2)
两式相减得:
Tn=(3n-2)×2n+1-3×22-3×23-…-3×2n-2
=(3n-5)×2n+1+10.
一.填空题(本大题共18小题,每小题5分,共90分)
1. 下列赋值语句中正确的是________.
①x←3; ②3←x;
③x-3←0; ④3-x←0.
解析:赋值语句一般是把值赋给左边的变量,只是一个字母,故只有①正确.
2.以下伪代码执行后,变量a,b的值分别为________.
a←15b←20a←a+bb←a-ba←a-bPrint a,b
解析:a的初始值为15,第3步a的值为35,第4步b的值为15,第5步a=35-15=20,故输出a=20,b=15.
3. 该伪代码运行后,输出的值y为________.
x←3If x>3 Then y←x×xElse y←2×xEnd IfPrint y
解析:y=∵x=3,∴y=6.
4.阅读下面的伪代码:
Read xIf x>1 Theny←x2+1Else y←2x+1End IfPrint y
若执行上述伪代码时没有执行y←x2+1,则输入的x的取值范围是________.
解析:(1)因为没有执行y←x2+1,所以x>1不成立,故x≤1.
5. (2011·江苏)根据下图所示的伪代码,当输入a,b分别为2,3时,最后输出的m的值是________.
6.执行下面的流程图,若p=4,则输出的S等于________.
解析:由流程图可知S=+++=.
7. 如图所示的算法流程图,若输入的n是100,则输出的变量S的值是________.
(第7题)
(第8题)
8. 如图给出的是计算1+++…+的值的一个程序框图,其中判断框内应填入的条件是i>________.
9. 阅读下面的伪代码:
若要使这个算法执行的结果是计算1+2+3+…+1000,则S的初始值x=________.
答案:0
10. 已知伪代码如下,则输出结果S=________.
I←0S←0While I<6 I←I+2 S←S+I 2End WhilePrint S
解析:根据伪代码可知:第一次循环:I=2,S=22=4;第二次循环:I=4,S=4+42=20;第三次循环:I=6,S=20+62=56;因I=6,所以循环结束,S=56.
11.下列伪代码执行后输出的结果是________.
解析:该程序的功能是计算S=5+4+…+n到首次不小于14的n-1的值,可得n=1.
12.写出表示下列伪代码运算功能的算术表达式________.
解析:用“追踪”法:S=,i=2→S=+,i=3,…,S=++…+,i=10.
答案:S=++…+
13.执行如图所示的流程图,则输出的结果为________.
第13题图 第14题图
解析:按照流程图依次执行为S=7,i=3,T=3;S=13,i=6,T=3+6=9;S=19,i=9,T=9+9=18;S=25,i=12,T=18+12=30.故最后输出T=30.
答案:30
14.在如图所示的流程图中,输入n=60,按程序运行后输出的结果是________.
解析:根据流程图可知,输出的结果是循环的次数.经过执行5次循环后n=1,所以输出的结果i=5.
15.(2009·江苏高考)如图是一个算法的流程图,最后输出的W等于________.
第15题图 第16题图
解析:第一次:T=1,
S=12-0=1;
第二次:T=3,
S=32-1=8;
第三次:T=5,
S=52-8=17.
此时满足S≥10.
所以W=S+T=17+5=22.
答案:22
16.如图所示流程图中,循环体执行的次数是________.
解析:从流程图反映的算法是S=2+4+6+8+…,I的初始值为2,由I=I+2知,执行了49次时,I=100,满足I≥100,退出循环.答案:49
17.下图是一个算法的流程图,则输出S的值是 ▲ .
18.执行如图所示的流程图,则输出的结果是________.
解析:如果把i<2010时的各个a值记作数列{an},那么这个程序第1次运行计算的是a2=,第2次运行计算的是a3=,…,第n次运行计算的是an+1=,故这个程序的功能是计算数列{an}的第2010项的值.将an+1=变形为=+1,故数列{}是首项为1,公差为1的等差数列,故=n,即an=,故输出结果是.
二.解答题(本大题共3小题,共30分)
19.如图,在边长为4的正方形ABCD的边上有一点P,它沿折线BCDA由B向A运动,设运动路程为x,△APB的面积为y,
(1)求y关于x的函数解析式,并指出其定义域.
(2)用伪代码写出根据输入的x的值计算y值的一个算法.
20.甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的流程图分别如图1和图2.
(1)根据图1和图2,当n=20时分别求出它们输出的结果;试判断甲、乙两位同学编写的流程图输出的结果是否一致?
(2)若希望通过对图2虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的流程图.
图1 图2
解:(1)图1中程序的功能是求2+4+6+8+…+2n的和,当n=20时,S=2+4+6+…+40=420.
图2中程序的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.
所以甲、乙两位同学编写的程序输出的结果是一致的.
(2)修改后部分流程图为:
21.已知数列{an}的各项均为正数,观察程序框图,当k=4时, ,当k=9时,
(1)试求数列{an}的通项;
(2)令bn=2nan,求b1+b2+…+bn的值.
(1)由框图知:
∵{an}为等差数列,设公差为d,
(2)设Tn=b1+b2+…+bn
=2×1+22×4+23×7+…+(3n-2)×2n
则2Tn=22×1+23×4+24×7+…+2n+1×(3n-2)
两式相减得:
Tn=(3n-2)×2n+1-3×22-3×23-…-3×2n-2
=(3n-5)×2n+1+10.
同课章节目录
