广东省中大附中2011-2012学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 广东省中大附中2011-2012学年高二下学期期中考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-12 00:00:00 | ||
图片预览


文档简介
考生注意事项:
⒈本试卷分第Ⅰ卷和第Ⅱ卷,用黑色钢笔、签字笔在答题卷上作答;
⒉考试时间 120分钟,全卷满分150分;
第Ⅰ卷 选择题(50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数等于
A. B. C. D.
2. “a>0” 是 “>0” 的
A.充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3.已知x与y之间的一组数据:
x 0 1 2 3
y 1 3 5 7
则y与x的线性回归方程为y=bx+a必过点
A . (2 , 2) B. (1 , 2) C. (1.5 , 4) D (1.5 , 0)
4.函数,已知f (x) 在x=-3时取得极值,则a=
A.2 B. 3 C. 4 D. 5
5. 抛物线的准线方程是
A. B. ( http: / / www. / ) C. D. ( http: / / www. / )
6.下列说法错误的是:
A.命题“”的逆否命题是:“”.
B.“ x>1 ” 是 “” 的充分不必要条件.
C.若且为假命题,则均为假命题.
D.命题 ,则
7.设,那么
A. ( http: / / www. / ) B.
C. ( http: / / www. / ) D.
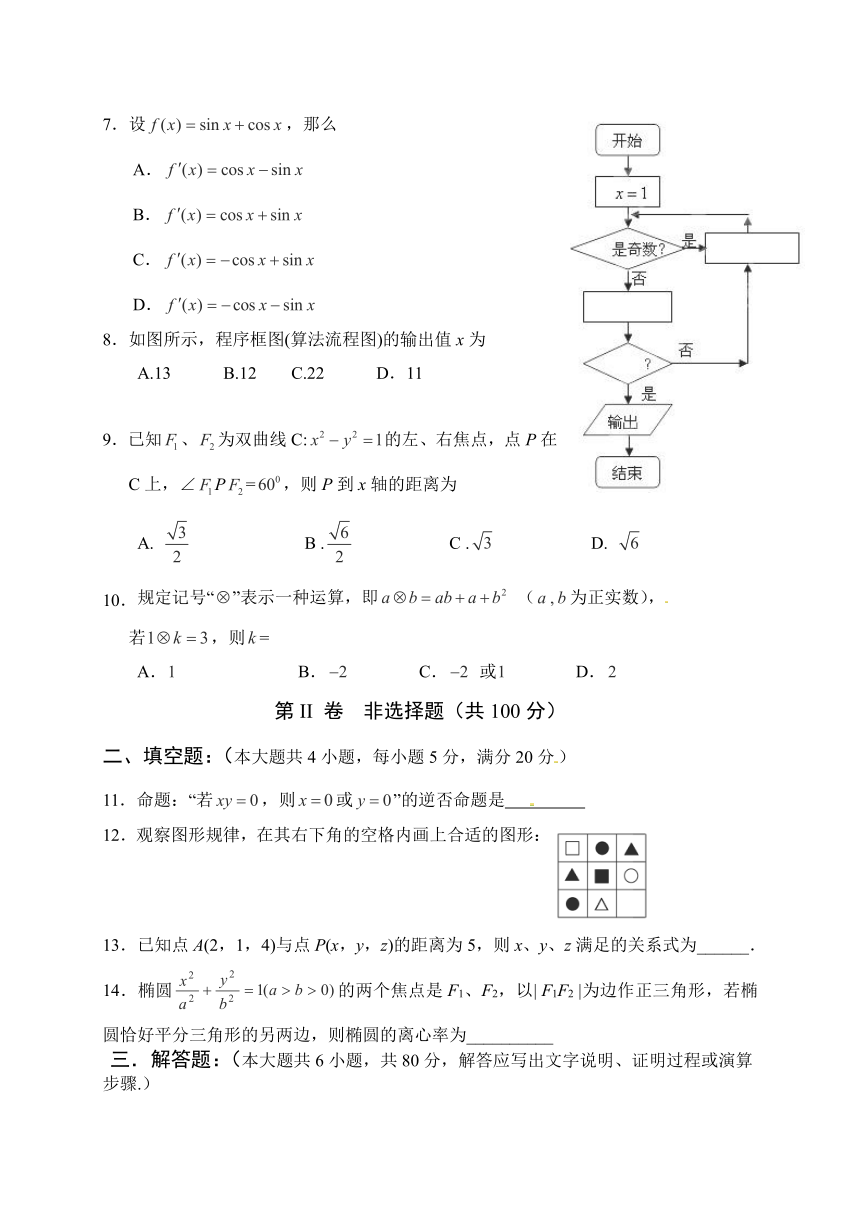
8.如图所示,程序框图(算法流程图)的输出值x为
A.13 B.12 C.22 D.11
9.已知、为双曲线C:的左、右焦点,点P在C上,∠P=,则P到x轴的距离为
A. B . C . D.
10.规定记号“”表示一种运算,即 (为正实数),
若,则=
A. B. C. 或 D.
第II 卷 非选择题(共100分)
二、填空题:(本大题共4小题,每小题5分,满分20分)
11.命题:“若,则或”的逆否命题是
12.观察图形规律,在其右下角的空格内画上合适的图形:
13.已知点A(2,1,4)与点P(x,y,z)的距离为5,则x、y、z满足的关系式为______.
14.椭圆的两个焦点是F1、F2,以| F1F2 |为边作正三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为__________
三.解答题:(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.)
15.(本题满分12分)
已知复数满足: 求的值.
16.(本小题满分12分)
已知双曲线的离心率等于2,且与椭圆 ( http: / / www. / )有相同的焦点,求此双曲线方程.
17、(本小题满分14分)
若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+.
请用反证法证明:a,b,c中至少有一个大于0.
18.(本小题满分14分)
如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求的长;
(2)求cos< >的值;
(3)求证:A1B⊥C1M.
19.(本小题满分14分)
已知顶点在原点,准线方程是的抛物线与过点的直线交于,两点,若直线和直线的斜率之和为1
(Ⅰ)求此抛物线的标准方程; (Ⅱ)求直线的方程。
20.(本小题满分14分)
已知函数f (x)=x 4-2ax2, aR.
(1)当a ≤ 0时,求函数f (x)的单调区间;
(2)当a <x<2a时,函数f (x)存在极小值,求a的取值范围;
(3)若x (0,1]时, 函数f (x)图象上任一点处的切线斜率均小于4, 求a的取值范围.
中大附中2011~2012学年度第二学期期中检测
高二数学答案(文科)
三、解答题:
15.解:设,而即
则--------------8分
------------------12分
16.解:∵ 椭圆的焦点坐标为(-4,0)和(4,0),……………………4分
则可设双曲线方程为 ( http: / / www. / )(a>0,b>0),………………6分
∵ c=4,又双曲线的离心率等于2,即,∴ a=2.……………………………8分
∴ ( http: / / www. / )=12. ………10分;故所求双曲线方程为. …………12分
17.证明: 假设a、b、c都不大于0---------------------------------------------2分
即a≤0,b≤0,c≤0---------------------------------------------------------------4分
所以a+b+c≤0---------------------------------------------------------------------6分
而a+b+c
=++----------------------------------8分
=(x2-2x)+(y2-2y)+(z2-2z)+π
=(x-1)2+(y-1)2+(z-1)2+π-3----------------------------------------------10分
所以a+b+c>0
这与a+b+c≤0矛盾--------------------------------------------------------------12分
故a、b、c中至少有一个大于0-------------------------------------------------14分
18.解:如图,建立空间直角坐标系O—xyz.
(1)依题意得B(0,1,0)、N(1,0,1)
∴| |=…………4分
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴={-1,-1,2},={0,1,2,},·=3,||=,||=
∴cos<,>=…………..10分
(3)证明:依题意,得C1(0,0,2)、M(,2),={-1,1,2},={,0}.∴·=-+0=0,∴⊥,∴A1B⊥C1M…………….14 分。
19.解:(Ⅰ)由题意可知抛物线焦点在轴正半轴,设抛物线的标准方程为
由准线方程是,可得
所以抛物线的标准方程为 6分
(Ⅱ)设直线的方程为:,
代人抛物线的标准方程消整理得
设,,则 ①
因为,,代人①,得 ②
因为,,代人②得
所以直线的方程为: 14分
20.解:(1)由题设知f '(x)=4x3-4ax,
令 f '(x)=0,得4x(x2-a)=0,
当a≤0时,得x=0, x<0时,f '(x)< 0;x>0时,f '(x)>0,
∴函数f(x)的单调递减区间是(-∞,0);单调递增区间是(0,+∞).---4分
(2)∵a<x<2a,∴a>0.
当a>0时,令f '(x)=0,得x=0或x=, ……………………..6分
列表如下:
x (-∞,-) (-,0) (0,) (,+∞)
f '(x) - + - +
f(x) 递减 递增 递减 递增
得x=-或x=时,f(x)极小= f(±)=-a2.
取x=-,由条件得 a<-<2a ,无解.
取x=, 由条件得 a<<2a ,解得<a<1.
综合上述:<a <1. -----------------------10分
图
⒈本试卷分第Ⅰ卷和第Ⅱ卷,用黑色钢笔、签字笔在答题卷上作答;
⒉考试时间 120分钟,全卷满分150分;
第Ⅰ卷 选择题(50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数等于
A. B. C. D.
2. “a>0” 是 “>0” 的
A.充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3.已知x与y之间的一组数据:
x 0 1 2 3
y 1 3 5 7
则y与x的线性回归方程为y=bx+a必过点
A . (2 , 2) B. (1 , 2) C. (1.5 , 4) D (1.5 , 0)
4.函数,已知f (x) 在x=-3时取得极值,则a=
A.2 B. 3 C. 4 D. 5
5. 抛物线的准线方程是
A. B. ( http: / / www. / ) C. D. ( http: / / www. / )
6.下列说法错误的是:
A.命题“”的逆否命题是:“”.
B.“ x>1 ” 是 “” 的充分不必要条件.
C.若且为假命题,则均为假命题.
D.命题 ,则
7.设,那么
A. ( http: / / www. / ) B.
C. ( http: / / www. / ) D.
8.如图所示,程序框图(算法流程图)的输出值x为
A.13 B.12 C.22 D.11
9.已知、为双曲线C:的左、右焦点,点P在C上,∠P=,则P到x轴的距离为
A. B . C . D.
10.规定记号“”表示一种运算,即 (为正实数),
若,则=
A. B. C. 或 D.
第II 卷 非选择题(共100分)
二、填空题:(本大题共4小题,每小题5分,满分20分)
11.命题:“若,则或”的逆否命题是
12.观察图形规律,在其右下角的空格内画上合适的图形:
13.已知点A(2,1,4)与点P(x,y,z)的距离为5,则x、y、z满足的关系式为______.
14.椭圆的两个焦点是F1、F2,以| F1F2 |为边作正三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为__________
三.解答题:(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.)
15.(本题满分12分)
已知复数满足: 求的值.
16.(本小题满分12分)
已知双曲线的离心率等于2,且与椭圆 ( http: / / www. / )有相同的焦点,求此双曲线方程.
17、(本小题满分14分)
若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+.
请用反证法证明:a,b,c中至少有一个大于0.
18.(本小题满分14分)
如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求的长;
(2)求cos< >的值;
(3)求证:A1B⊥C1M.
19.(本小题满分14分)
已知顶点在原点,准线方程是的抛物线与过点的直线交于,两点,若直线和直线的斜率之和为1
(Ⅰ)求此抛物线的标准方程; (Ⅱ)求直线的方程。
20.(本小题满分14分)
已知函数f (x)=x 4-2ax2, aR.
(1)当a ≤ 0时,求函数f (x)的单调区间;
(2)当a <x<2a时,函数f (x)存在极小值,求a的取值范围;
(3)若x (0,1]时, 函数f (x)图象上任一点处的切线斜率均小于4, 求a的取值范围.
中大附中2011~2012学年度第二学期期中检测
高二数学答案(文科)
三、解答题:
15.解:设,而即
则--------------8分
------------------12分
16.解:∵ 椭圆的焦点坐标为(-4,0)和(4,0),……………………4分
则可设双曲线方程为 ( http: / / www. / )(a>0,b>0),………………6分
∵ c=4,又双曲线的离心率等于2,即,∴ a=2.……………………………8分
∴ ( http: / / www. / )=12. ………10分;故所求双曲线方程为. …………12分
17.证明: 假设a、b、c都不大于0---------------------------------------------2分
即a≤0,b≤0,c≤0---------------------------------------------------------------4分
所以a+b+c≤0---------------------------------------------------------------------6分
而a+b+c
=++----------------------------------8分
=(x2-2x)+(y2-2y)+(z2-2z)+π
=(x-1)2+(y-1)2+(z-1)2+π-3----------------------------------------------10分
所以a+b+c>0
这与a+b+c≤0矛盾--------------------------------------------------------------12分
故a、b、c中至少有一个大于0-------------------------------------------------14分
18.解:如图,建立空间直角坐标系O—xyz.
(1)依题意得B(0,1,0)、N(1,0,1)
∴| |=…………4分
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴={-1,-1,2},={0,1,2,},·=3,||=,||=
∴cos<,>=…………..10分
(3)证明:依题意,得C1(0,0,2)、M(,2),={-1,1,2},={,0}.∴·=-+0=0,∴⊥,∴A1B⊥C1M…………….14 分。
19.解:(Ⅰ)由题意可知抛物线焦点在轴正半轴,设抛物线的标准方程为
由准线方程是,可得
所以抛物线的标准方程为 6分
(Ⅱ)设直线的方程为:,
代人抛物线的标准方程消整理得
设,,则 ①
因为,,代人①,得 ②
因为,,代人②得
所以直线的方程为: 14分
20.解:(1)由题设知f '(x)=4x3-4ax,
令 f '(x)=0,得4x(x2-a)=0,
当a≤0时,得x=0, x<0时,f '(x)< 0;x>0时,f '(x)>0,
∴函数f(x)的单调递减区间是(-∞,0);单调递增区间是(0,+∞).---4分
(2)∵a<x<2a,∴a>0.
当a>0时,令f '(x)=0,得x=0或x=, ……………………..6分
列表如下:
x (-∞,-) (-,0) (0,) (,+∞)
f '(x) - + - +
f(x) 递减 递增 递减 递增
得x=-或x=时,f(x)极小= f(±)=-a2.
取x=-,由条件得 a<-<2a ,无解.
取x=, 由条件得 a<<2a ,解得<a<1.
综合上述:<a <1. -----------------------10分
图
同课章节目录
