2020--2021学年北师大版八年级下册数学6.2 平行四边形的判定同步检测(word含答案)
文档属性
| 名称 | 2020--2021学年北师大版八年级下册数学6.2 平行四边形的判定同步检测(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 464.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 05:32:03 | ||
图片预览



文档简介
第六章第二节 平行四边形的判定
一、选择题(共9小题;共27分)
1. 如图,4×4 的方格中每个小正方形的边长都是 1,则 S四边形ABCD 与 S四边形ECDF 的大小关系是 ??
A. S四边形ABCD=S四边形ECDF B. S四边形ABCD C. S四边形ABCD=S四边形ECDF+1 D. S四边形ABCD=S四边形ECDF+2
2. 在四边形 ABCD 中,∠A,∠B,∠C,∠D 的度数之比如下,其中能判断四边形 ABCD 是平行四边形的是 ??
A. 1:2:3:4 B. 2:3:4:5 C. 3:2:3:2 D. 3:3:5:5
3. 若以 A?0.5,0,B2,0,C0,1 三点为顶点画平行四边形,则第四个顶点不可能在 ??
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 如图所示,在平行四边形 ABCD 中,E,F 分别为一组对边的中点,则图中平行四边形有 ??
A. 4 个 B. 6 个 C. 7 个 D. 8 个
5. 如图所示,AB∥CD∥EF,BC∥AD,AC 为 ∠BAD 的平分线,图中与 ∠AOE 相等(不含 ∠AOE)的角有 ??
A. 2 个 B. 3 个 C. 4 个 D. 5 个
6. 下列说法不正确的有 ??
①如果一个四边形的任意相邻的两个内角都互补,那么这个四边形是平行四边形
②一组对边平行,另一组对边相等的四边形是平行四边形
③如果 AC,BD 为四边形 ABCD 的对角线,且 AC 平分 BD,那么四边形 ABCD 是平行四边形
④两组对角分别相等的四边形是平行四边形
A. 1 个 B. 2 个 C. 3 个 D. 4 个
7. 在同一平面内,直线 a∥c,且直线 a 到直线 c 的距离是 2.直线 b∥c,直线 b 到直线 c 的距离为 5,则直线 a 到直线 b 的距离为 ??
A. 3 B. 7 C. 3 或 7 D. 无法确定
8. 如图所示,在一块平地上,雨后中间有一条积水沟,沟的两边是平行的,一只蚂蚁在 A 点,想越过水沟到 B 点取食,几位学生在沟上沿与沟边垂直的方向放了 4 根小木棍,这只蚂蚁通过几号木棍时,才能使从 A 到 B 的路径最短 ??
A. 1 号 B. 2 号 C. 3 号 D. 4 号
9. 如图所示,直线 m∥n,A,B 为直线 n 上两点,C,D 为直线 m 上两点,BC 与 AD 交于点 O,则图中面积相等的三角形有 ??
A. 1 对 B. 2 对 C. 3 对 D. 4 对
二、填空题(共13小题;共39分)
10. 如图,方格纸中每个最小正方形的边长为 1 ,则两平行直线 AB 、 CD 之间的距离是 ?.
11. 在四边形 ABCD 中,AB=CD,再添加一个条件 ?(写出一个即可),则四边形 ABCD 是平行四边形.
12. 如图,DE∥BC,AE=EC,延长 DE 到 F,使 EF=DE,连接 AF,FC,CD,则图中四边形 ADCF 是 ?.
13. 已知 AB∥CD∥EF,BC∥AD,AC 为 ∠BAD 的平分线,图中与 ∠COF 相等(不含 ∠COF)的角有 ? 个.
14. 如图所示,点 E,F 分别在长方形 ABCD 的边 AB,CD 上,且 AF∥CE,AB=3,AD=5,那么 AE 与 CF 的距离是 ?.
15. 如图所示,在平行四边形 ABCD 中,E,F 分别为边 AB,CD 的中点,则图中共有 ? 个平行四边形.
16. 如图所示,已知正三角形的边长为 8,M 为三角形内一点,过点 M 分别作三边的平行线,则 MD+ME+MF= ?.
17. 一个四边形的边长依次为 a,b,c,d,且满足 a2+b2+c2+d2=2ac+2bd,则这个四边形的形状为 ?.
18. 在四边形 ABCD 中,AD=BC,BD 为对角线,∠ADB=∠CBD,则 AB 与 CD 的关系是 ?.
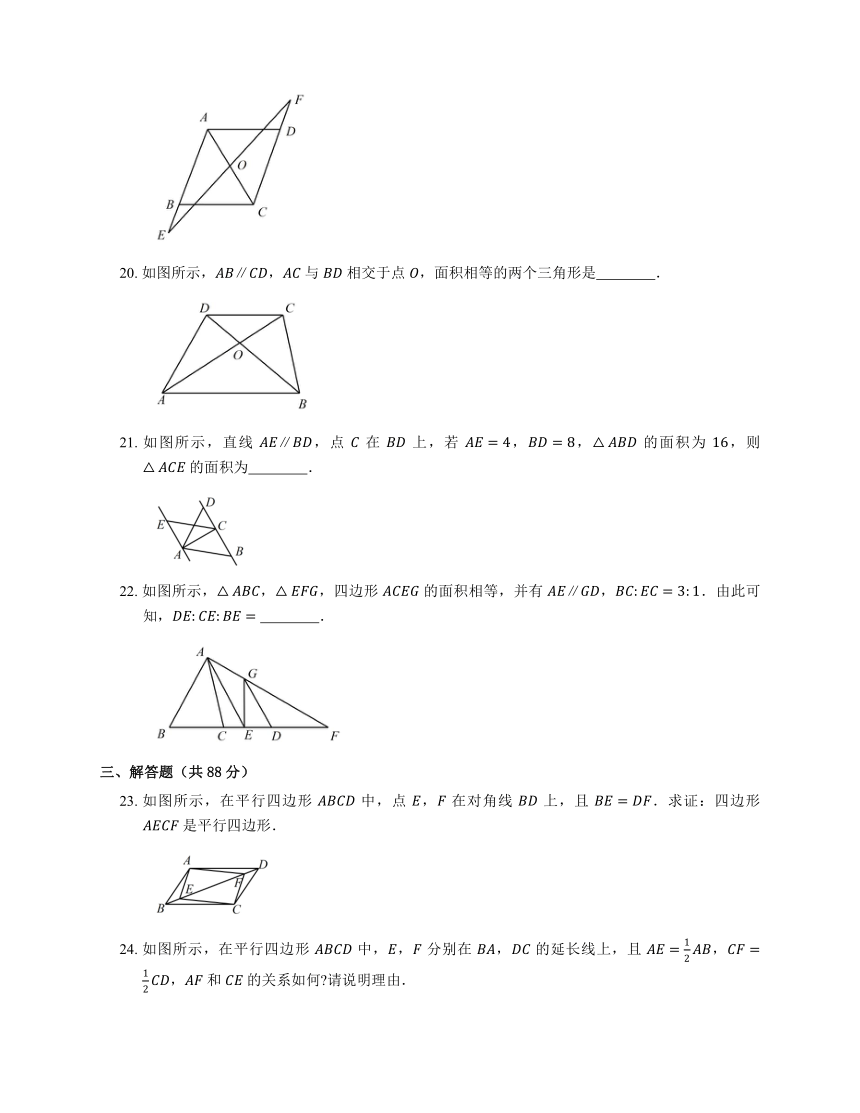
19. 如图所示,在平行四边形 ABCD 中,延长 AB 到 E,延长 CD 到 F,使 BE=DF,则线段 AC 与 EF 的关系是 ?.
20. 如图所示,AB∥CD,AC 与 BD 相交于点 O,面积相等的两个三角形是 ?.
21. 如图所示,直线 AE∥BD,点 C 在 BD 上,若 AE=4,BD=8,△ABD 的面积为 16,则 △ACE 的面积为 ?.
22. 如图所示,△ABC,△EFG,四边形 ACEG 的面积相等,并有 AE∥GD,BC:EC=3:1.由此可知,DE:CE:BE= ?.
三、解答题(共88分)
23. 如图所示,在平行四边形 ABCD 中,点 E,F 在对角线 BD 上,且 BE=DF.求证:四边形 AECF 是平行四边形.
24. 如图所示,在平行四边形 ABCD 中,E,F 分别在 BA,DC 的延长线上,且 AE=12AB,CF=12CD,AF 和 CE 的关系如何?请说明理由.
25. 如图所示,AC 是平行四边形 ABCD 的对角线.
(1)请按如下步骤在图中完成作图(保留作图痕迹).
①分别以点 A,C 为圆心,以大于 12AC 长为半径画弧,弧在 AC 两侧的交点分别为 P,Q;
②连接 PQ,PQ 分别与 AB,AC,CD 交于点 E,O,F.
(2)求证:AE=CF.
26. 如图所示,在 △ABC 中,点 D,E 分别是 AB,AC 边的中点.若把 △ADE 绕着点 E 按顺时针方向旋转 180? ,得到 △CFE .
(1)请指出图中哪些线段与线段 CF 相等;
(2)试判断四边形 DBCF 是怎样的四边形,并证明你的结论.
27. 如图,E,F 是四边形 ABCD 的对角线 AC 上两点,AF=CE,DF=BE,DF∥BE.求证:
(1)△AFD≌△CEB;
(2)四边形 ABCD 是平行四边形.
28. 如图所示,在四边形 ABCD 中,OE=OF,OA=OC,且 AD∥BC.求证:AD=BC.
29. 如图所示,在平行四边形 ABCD 中,M,N 分别为 AD,BC 的中点,连接 AN,DN,BM,CM,且 AN,BM 交于点 P,CM,DN 交于点 Q.四边形 MQNP 是平行四边形吗?为什么?
30. 如图,已知 BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形 DEBF 是平行四边形.
答案
1. A 【解析】S四边形ABCD=CD?AC=1×4=4,S四边形ECDF=CD?AC=1×4=4.
2. C
3. C
4. B
5. D
6. B
7. C
8. B
9. C
10. 3
11. AD=BC
12. 平行四边形
13. 5
14. 5
15. 4
16. 8
17. 平行四边形
18. AB=CD 且 AB∥CD
19. 互相平分
20. △ABD 和 △ABC,△AOD 和 △BOC,△ACD 和 △BCD
21. 8
22. 2:1:4
23. 连接 AC,与 BD 交于点 O.
通过证明 △AOE≌△COF,
得 AE=CF,∠AEF=∠CFE,AE∥CF,
从而可证四边形 AECF 是平行四边形.
24. AF∥CE,AF=CE.
证明:∵ 四边形 ABCD 是平行四边形,
∴AB=CD,AB∥CD.
∵AE=12AB,CF=12CD,
∴AE=CF,AE∥CF.
∴ 四边形 AECF 是平行四边形,
∴AF∥CE,AF=CE.
25. (1) 如图所示.
??????(2) 由(1)知,PQ 垂直平分 AC .
∵ 平行四边形 ABCD ,
∴∠DCA=∠BAC ,
∴△OCF≌△OAE,得出 AE=CF.
26. (1) AD=CF,DB=CF .
??????(2) 四边形 DBCF 是平行四边形.
证明:将 △ADE 绕点 E 顺时针旋转 180? ,得到 △CFE,∵△ADE≌△CFE .
∴AD=CF,∠A=∠ECF . ∴AB∥CF .
又 ∵D 是 AB 的中点,∴AD=DB=CF ,
∴ 四边形 DBCF 是平行四边形.
27. (1) ∵DF∥BE,
∴∠DFE=∠BEF.
∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
??????(2) 由(1)知 △AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC.
∴AD∥BC.
∴ 四边形 ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形).
28. 连接 AE,CF,
∵OE=OF,OA=OC,
∴ 四边形 AFCE 是平行四边形.
∴DC∥AB.
∵AD∥BC,
∴ 四边形 ABCD 是平行四边形.
∴AD=BC.
29. 四边形 MQNP 是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴AD∥BC,AD=BC.
∵M,N 分别是 AD,BC 的中点,
∴MD∥BN,MD=BN,AM=CN,AM∥CN.
∴ 四边形 BNDM 与四边形 ANCM 是平行四边形.
∴AN∥CM,BM∥DN.
∴ 四边形 MQNP 是平行四边形.
30. ∵BE∥DF,
∴∠BEC=∠DFA,
在 △ADF 和 △CBE 中,
∠ADF=∠CBE,∠AFD=∠CEB,AF=CE,
∴△ADF≌△CBE AAS.
∴BE=DF.
又 BE∥DF,
∴ 四边形 DEBF 是平行四边形.
一、选择题(共9小题;共27分)
1. 如图,4×4 的方格中每个小正方形的边长都是 1,则 S四边形ABCD 与 S四边形ECDF 的大小关系是 ??
A. S四边形ABCD=S四边形ECDF B. S四边形ABCD
2. 在四边形 ABCD 中,∠A,∠B,∠C,∠D 的度数之比如下,其中能判断四边形 ABCD 是平行四边形的是 ??
A. 1:2:3:4 B. 2:3:4:5 C. 3:2:3:2 D. 3:3:5:5
3. 若以 A?0.5,0,B2,0,C0,1 三点为顶点画平行四边形,则第四个顶点不可能在 ??
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 如图所示,在平行四边形 ABCD 中,E,F 分别为一组对边的中点,则图中平行四边形有 ??
A. 4 个 B. 6 个 C. 7 个 D. 8 个
5. 如图所示,AB∥CD∥EF,BC∥AD,AC 为 ∠BAD 的平分线,图中与 ∠AOE 相等(不含 ∠AOE)的角有 ??
A. 2 个 B. 3 个 C. 4 个 D. 5 个
6. 下列说法不正确的有 ??
①如果一个四边形的任意相邻的两个内角都互补,那么这个四边形是平行四边形
②一组对边平行,另一组对边相等的四边形是平行四边形
③如果 AC,BD 为四边形 ABCD 的对角线,且 AC 平分 BD,那么四边形 ABCD 是平行四边形
④两组对角分别相等的四边形是平行四边形
A. 1 个 B. 2 个 C. 3 个 D. 4 个
7. 在同一平面内,直线 a∥c,且直线 a 到直线 c 的距离是 2.直线 b∥c,直线 b 到直线 c 的距离为 5,则直线 a 到直线 b 的距离为 ??
A. 3 B. 7 C. 3 或 7 D. 无法确定
8. 如图所示,在一块平地上,雨后中间有一条积水沟,沟的两边是平行的,一只蚂蚁在 A 点,想越过水沟到 B 点取食,几位学生在沟上沿与沟边垂直的方向放了 4 根小木棍,这只蚂蚁通过几号木棍时,才能使从 A 到 B 的路径最短 ??
A. 1 号 B. 2 号 C. 3 号 D. 4 号
9. 如图所示,直线 m∥n,A,B 为直线 n 上两点,C,D 为直线 m 上两点,BC 与 AD 交于点 O,则图中面积相等的三角形有 ??
A. 1 对 B. 2 对 C. 3 对 D. 4 对
二、填空题(共13小题;共39分)
10. 如图,方格纸中每个最小正方形的边长为 1 ,则两平行直线 AB 、 CD 之间的距离是 ?.
11. 在四边形 ABCD 中,AB=CD,再添加一个条件 ?(写出一个即可),则四边形 ABCD 是平行四边形.
12. 如图,DE∥BC,AE=EC,延长 DE 到 F,使 EF=DE,连接 AF,FC,CD,则图中四边形 ADCF 是 ?.
13. 已知 AB∥CD∥EF,BC∥AD,AC 为 ∠BAD 的平分线,图中与 ∠COF 相等(不含 ∠COF)的角有 ? 个.
14. 如图所示,点 E,F 分别在长方形 ABCD 的边 AB,CD 上,且 AF∥CE,AB=3,AD=5,那么 AE 与 CF 的距离是 ?.
15. 如图所示,在平行四边形 ABCD 中,E,F 分别为边 AB,CD 的中点,则图中共有 ? 个平行四边形.
16. 如图所示,已知正三角形的边长为 8,M 为三角形内一点,过点 M 分别作三边的平行线,则 MD+ME+MF= ?.
17. 一个四边形的边长依次为 a,b,c,d,且满足 a2+b2+c2+d2=2ac+2bd,则这个四边形的形状为 ?.
18. 在四边形 ABCD 中,AD=BC,BD 为对角线,∠ADB=∠CBD,则 AB 与 CD 的关系是 ?.
19. 如图所示,在平行四边形 ABCD 中,延长 AB 到 E,延长 CD 到 F,使 BE=DF,则线段 AC 与 EF 的关系是 ?.
20. 如图所示,AB∥CD,AC 与 BD 相交于点 O,面积相等的两个三角形是 ?.
21. 如图所示,直线 AE∥BD,点 C 在 BD 上,若 AE=4,BD=8,△ABD 的面积为 16,则 △ACE 的面积为 ?.
22. 如图所示,△ABC,△EFG,四边形 ACEG 的面积相等,并有 AE∥GD,BC:EC=3:1.由此可知,DE:CE:BE= ?.
三、解答题(共88分)
23. 如图所示,在平行四边形 ABCD 中,点 E,F 在对角线 BD 上,且 BE=DF.求证:四边形 AECF 是平行四边形.
24. 如图所示,在平行四边形 ABCD 中,E,F 分别在 BA,DC 的延长线上,且 AE=12AB,CF=12CD,AF 和 CE 的关系如何?请说明理由.
25. 如图所示,AC 是平行四边形 ABCD 的对角线.
(1)请按如下步骤在图中完成作图(保留作图痕迹).
①分别以点 A,C 为圆心,以大于 12AC 长为半径画弧,弧在 AC 两侧的交点分别为 P,Q;
②连接 PQ,PQ 分别与 AB,AC,CD 交于点 E,O,F.
(2)求证:AE=CF.
26. 如图所示,在 △ABC 中,点 D,E 分别是 AB,AC 边的中点.若把 △ADE 绕着点 E 按顺时针方向旋转 180? ,得到 △CFE .
(1)请指出图中哪些线段与线段 CF 相等;
(2)试判断四边形 DBCF 是怎样的四边形,并证明你的结论.
27. 如图,E,F 是四边形 ABCD 的对角线 AC 上两点,AF=CE,DF=BE,DF∥BE.求证:
(1)△AFD≌△CEB;
(2)四边形 ABCD 是平行四边形.
28. 如图所示,在四边形 ABCD 中,OE=OF,OA=OC,且 AD∥BC.求证:AD=BC.
29. 如图所示,在平行四边形 ABCD 中,M,N 分别为 AD,BC 的中点,连接 AN,DN,BM,CM,且 AN,BM 交于点 P,CM,DN 交于点 Q.四边形 MQNP 是平行四边形吗?为什么?
30. 如图,已知 BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形 DEBF 是平行四边形.
答案
1. A 【解析】S四边形ABCD=CD?AC=1×4=4,S四边形ECDF=CD?AC=1×4=4.
2. C
3. C
4. B
5. D
6. B
7. C
8. B
9. C
10. 3
11. AD=BC
12. 平行四边形
13. 5
14. 5
15. 4
16. 8
17. 平行四边形
18. AB=CD 且 AB∥CD
19. 互相平分
20. △ABD 和 △ABC,△AOD 和 △BOC,△ACD 和 △BCD
21. 8
22. 2:1:4
23. 连接 AC,与 BD 交于点 O.
通过证明 △AOE≌△COF,
得 AE=CF,∠AEF=∠CFE,AE∥CF,
从而可证四边形 AECF 是平行四边形.
24. AF∥CE,AF=CE.
证明:∵ 四边形 ABCD 是平行四边形,
∴AB=CD,AB∥CD.
∵AE=12AB,CF=12CD,
∴AE=CF,AE∥CF.
∴ 四边形 AECF 是平行四边形,
∴AF∥CE,AF=CE.
25. (1) 如图所示.
??????(2) 由(1)知,PQ 垂直平分 AC .
∵ 平行四边形 ABCD ,
∴∠DCA=∠BAC ,
∴△OCF≌△OAE,得出 AE=CF.
26. (1) AD=CF,DB=CF .
??????(2) 四边形 DBCF 是平行四边形.
证明:将 △ADE 绕点 E 顺时针旋转 180? ,得到 △CFE,∵△ADE≌△CFE .
∴AD=CF,∠A=∠ECF . ∴AB∥CF .
又 ∵D 是 AB 的中点,∴AD=DB=CF ,
∴ 四边形 DBCF 是平行四边形.
27. (1) ∵DF∥BE,
∴∠DFE=∠BEF.
∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
??????(2) 由(1)知 △AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC.
∴AD∥BC.
∴ 四边形 ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形).
28. 连接 AE,CF,
∵OE=OF,OA=OC,
∴ 四边形 AFCE 是平行四边形.
∴DC∥AB.
∵AD∥BC,
∴ 四边形 ABCD 是平行四边形.
∴AD=BC.
29. 四边形 MQNP 是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴AD∥BC,AD=BC.
∵M,N 分别是 AD,BC 的中点,
∴MD∥BN,MD=BN,AM=CN,AM∥CN.
∴ 四边形 BNDM 与四边形 ANCM 是平行四边形.
∴AN∥CM,BM∥DN.
∴ 四边形 MQNP 是平行四边形.
30. ∵BE∥DF,
∴∠BEC=∠DFA,
在 △ADF 和 △CBE 中,
∠ADF=∠CBE,∠AFD=∠CEB,AF=CE,
∴△ADF≌△CBE AAS.
∴BE=DF.
又 BE∥DF,
∴ 四边形 DEBF 是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
