2021-2022学年 北师大新版 七年级上册数学 第1章 丰富的图形世界 单元测试卷 (Word版 含解析)
文档属性
| 名称 | 2021-2022学年 北师大新版 七年级上册数学 第1章 丰富的图形世界 单元测试卷 (Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 05:58:33 | ||
图片预览

文档简介
2021-2022学年北师大新版七年级上册数学《第1章
丰富的图形世界》单元测试卷
一.选择题
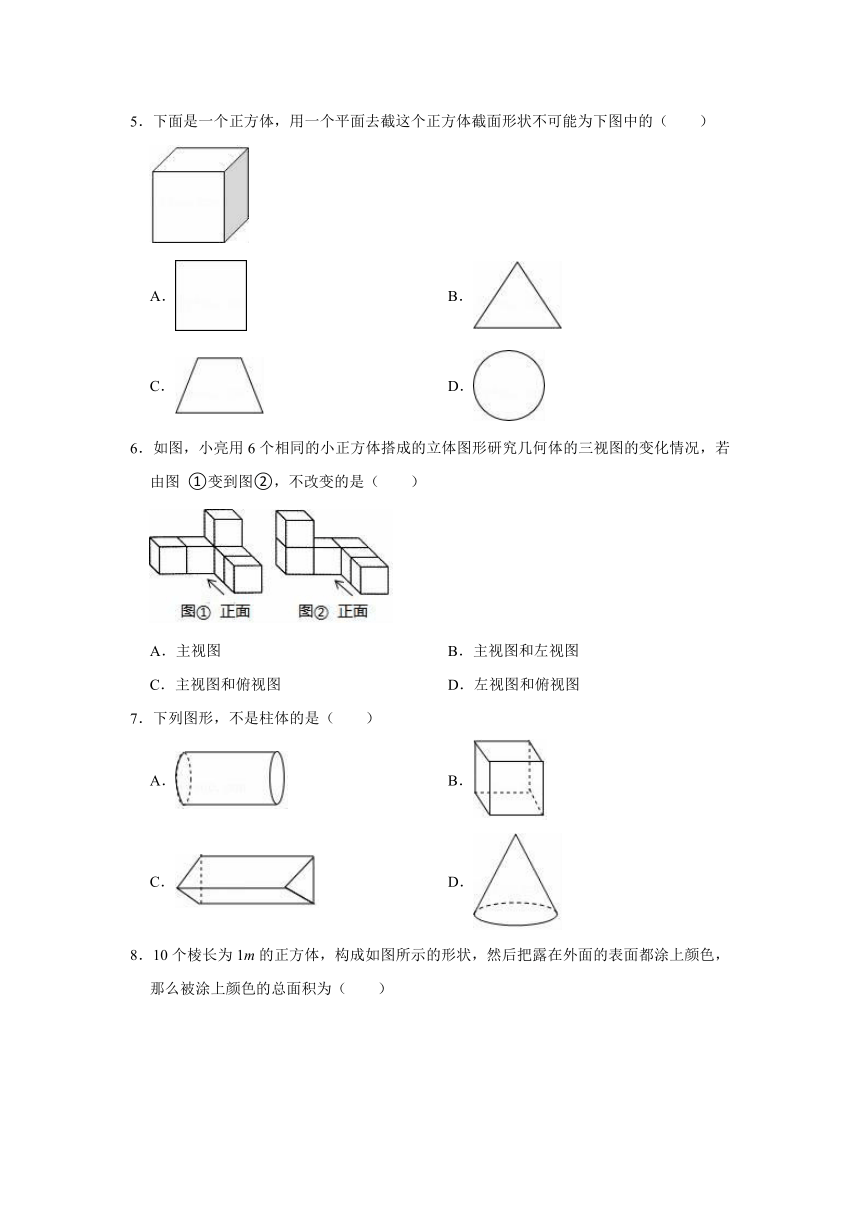
1.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A.
B.
C.
D.
2.如图是一个正方体的表面展开图,在这个正方体中,与点A重合的点为( )
A.点C和点N
B.点B和点M
C.点C和点M
D.点B和点N
3.下列图形(如图所示)经过折叠不能围成正方体的是( )
A.
B.
C.
D.
4.小刚同学在一个正方体盒子的每个面都写了一个字,分别是:我、喜、欢、数、学、课.其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )
A.课
B.欢
C.数
D.学
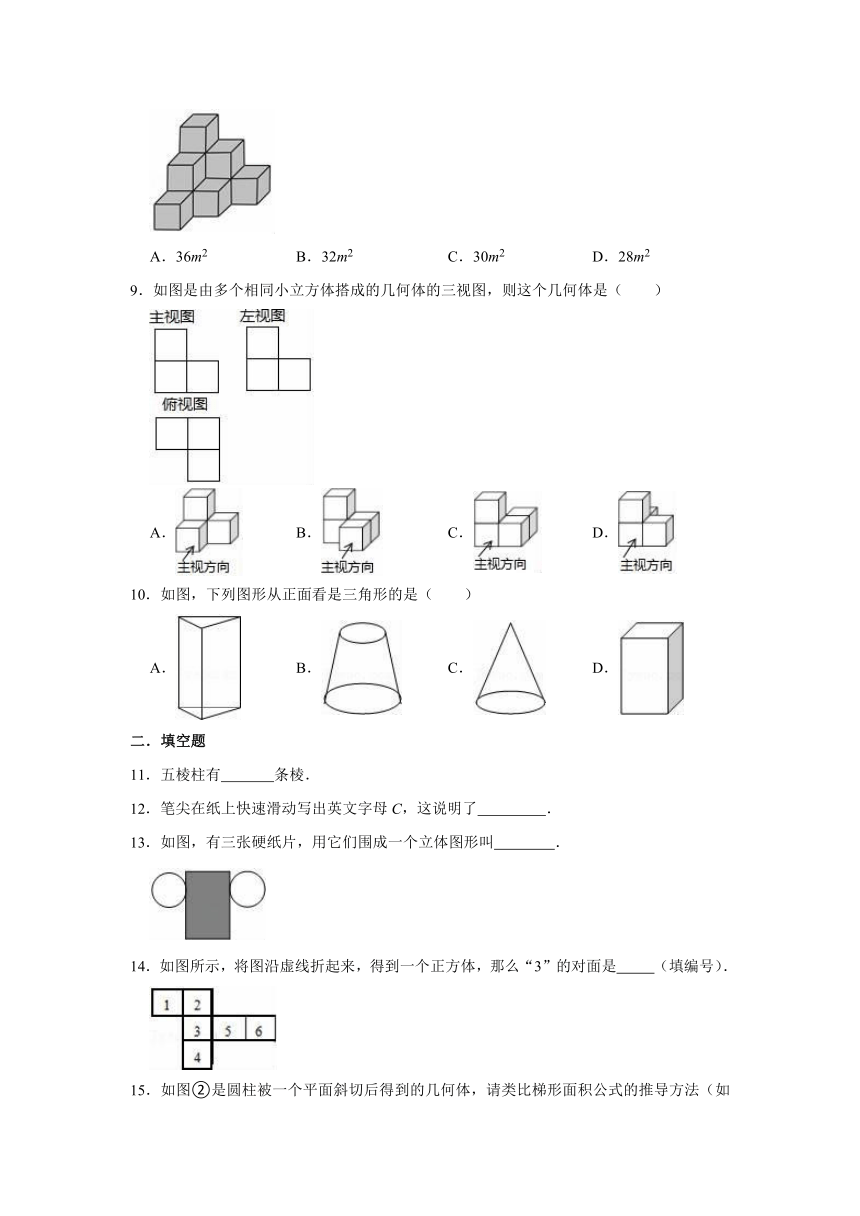
5.下面是一个正方体,用一个平面去截这个正方体截面形状不可能为下图中的( )
A.
B.
C.
D.
6.如图,小亮用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图
①变到图②,不改变的是( )
A.主视图
B.主视图和左视图
C.主视图和俯视图
D.左视图和俯视图
7.下列图形,不是柱体的是( )
A.
B.
C.
D.
8.10个棱长为1m的正方体,构成如图所示的形状,然后把露在外面的表面都涂上颜色,那么被涂上颜色的总面积为( )
A.36m2
B.32m2
C.30m2
D.28m2
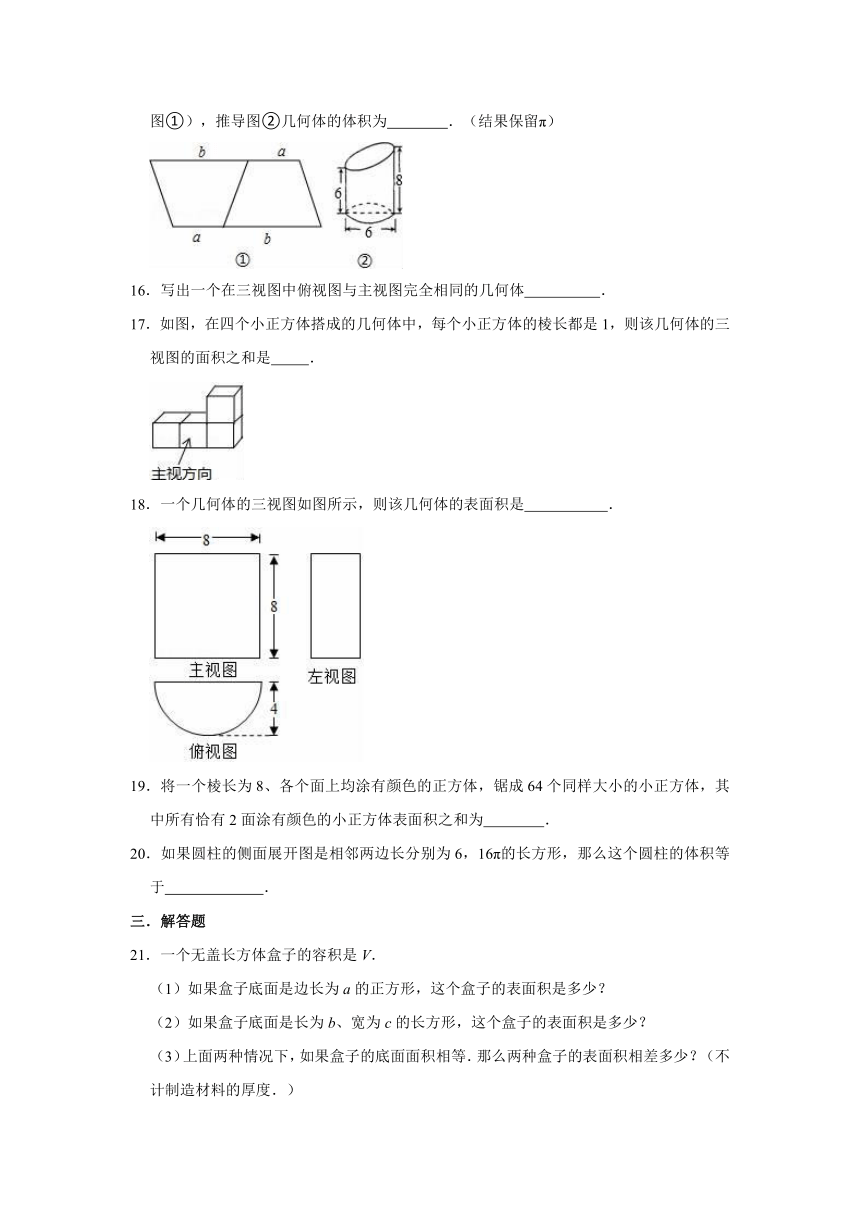
9.如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( )
A.
B.
C.
D.
10.如图,下列图形从正面看是三角形的是( )
A.
B.
C.
D.
二.填空题
11.五棱柱有
条棱.
12.笔尖在纸上快速滑动写出英文字母C,这说明了
.
13.如图,有三张硬纸片,用它们围成一个立体图形叫
.
14.如图所示,将图沿虚线折起来,得到一个正方体,那么“3”的对面是
(填编号).
15.如图②是圆柱被一个平面斜切后得到的几何体,请类比梯形面积公式的推导方法(如图①),推导图②几何体的体积为
.(结果保留π)
16.写出一个在三视图中俯视图与主视图完全相同的几何体
.
17.如图,在四个小正方体搭成的几何体中,每个小正方体的棱长都是1,则该几何体的三视图的面积之和是
.
18.一个几何体的三视图如图所示,则该几何体的表面积是
.
19.将一个棱长为8、各个面上均涂有颜色的正方体,锯成64个同样大小的小正方体,其中所有恰有2面涂有颜色的小正方体表面积之和为
.
20.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于
.
三.解答题
21.一个无盖长方体盒子的容积是V.
(1)如果盒子底面是边长为a的正方形,这个盒子的表面积是多少?
(2)如果盒子底面是长为b、宽为c的长方形,这个盒子的表面积是多少?
(3)上面两种情况下,如果盒子的底面面积相等.那么两种盒子的表面积相差多少?(不计制造材料的厚度.)
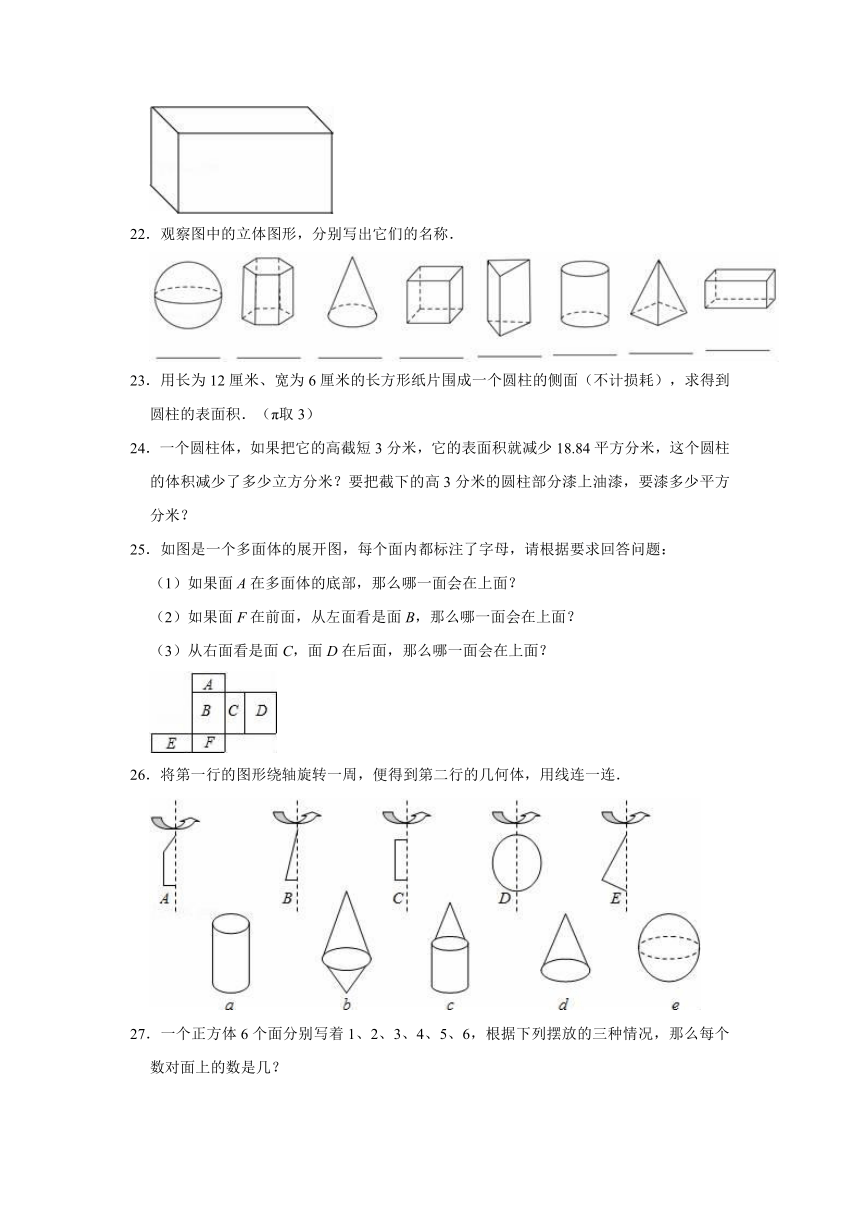
22.观察图中的立体图形,分别写出它们的名称.
23.用长为12厘米、宽为6厘米的长方形纸片围成一个圆柱的侧面(不计损耗),求得到圆柱的表面积.(π取3)
24.一个圆柱体,如果把它的高截短3分米,它的表面积就减少18.84平方分米,这个圆柱的体积减少了多少立方分米?要把截下的高3分米的圆柱部分漆上油漆,要漆多少平方分米?
25.如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
26.将第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
27.一个正方体6个面分别写着1、2、3、4、5、6,根据下列摆放的三种情况,那么每个数对面上的数是几?
参考答案与试题解析
一.选择题
1.解:A、是两个圆台,故A错误;
B、上面小下面大,侧面是曲面,故B正确;
C、是一个圆台,故C错误;
D、下面小上面大侧面是曲面,故D错误;
故选:B.
2.解:折叠成正方体时,与点A重合的点为C、N.
故选:A.
3.解:A、C、D经过折叠均能围成正方体,
B折叠后第一行两个面无法折起来,而且下边没有面,不能折成正方体.
故选:B.
4.解:正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,
所以该正方体盒子上,“我”相对的面上所写的文字是“课”;
故选:A.
5.解:无论如何去截,截面也不可能有弧度,因此截面不可能是圆.
故选:D.
6.解:从左面看第一层都是三个小正方形,第二层左边一个小正方形,①②的左视图相同;
从上面看第一列都是一个小正方形,第二列都是一个小正方形,第三列都是三个小正方形,故①②的俯视图相同,
故选:D.
7.解:长方体是四棱柱,三棱柱是柱体,圆锥是锥体,圆柱是柱体,
故选:D.
8.解:∵要染色的上底面有6个,侧面有24个,
∴被染色的图形的面积是:(24+6)×(1×1)=30(m2),
故选:C.
9.解:从主视图看第一列两个正方体,说明俯视图中的左边一列有两个正方体,主视图右边的一列只有一行,说明俯视图中的右边一列两行都只有一个正方体,所以此几何体如图所示:.
故选:B.
10.解:A、三棱柱从正面看到的是长方形,不合题意;
B、圆台从正面看到的是梯形,不合题意;
C、圆锥从正面看到的是三角形,符合题意;
D、长方体从正面看到的是长方形,不合题意.
故选:C.
二.填空题
11.解:五棱柱有侧棱5条,
底面上的棱5×2=10条,
所以,共有5+10=15条.
故答案为:15.
12.解:笔尖在纸上快速滑动写出英文字母C,这说明了点动成线;
故答案为:点动成线
13.解:利用三视图有关知识,矩形只能组成圆柱形,两个圆正好组成圆柱的上底与下底.
故填:圆柱体
14.解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,
∴在此正方体上与“3”相对的面上的数字是“6”.
故答案为:6.
15.解:π()2×(8﹣6)×+π()2×6,
=9π+54π
=63π.
故答案为:63π.
16.解:球的俯视图与主视图都为圆;
正方体的俯视图与主视图都为正方形.
故答案为:球或正方体(答案不唯一).
17.解:主视图是第一层是三个小正方形,第二层右边一个小正方形,主视图的面积是4,
俯视图是三个小正方形,俯视图的面积是3,
左视图是下边一个小正方形,第二层一个小正方形,左视图的面积是2,
几何体的三视图的面积之和是4+3+2=9,
故答案为:9.
18.解:由三视图可知:原几何体为圆柱的一半,(沿中轴线切开),
由题意可知,圆柱的高为8,底面圆的半径为4,
故其表面积为S=42π+4π×8+8×8=48π+64.
故答案为:48π+64.
19.解:根据以上分析:小正方体的棱长是2,表面积是2×2×6=24,恰有2面涂有颜色的小正方体共有24个.则这样的小正方体表面积的和是24×24=576.
故答案为576.
20.解:①底面周长为6,高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π,高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
三.解答题
21.解:(1)∵一个无盖长方体盒子的容积是V,盒子地面边长为a的正方形,
∴长方体盒子的高为:h=,
∴这个盒子的外表面积S1=a2+×4a=a2+;
(2)∵一个无盖长方体盒子的容积是V,盒子底面是长为b,宽为c的长方形,
∴长方体盒子的高为:h=,
∴这个盒子的外表面积S2=bc+×2(b+c)=bc+;
(3)∵盒子的底面积相等,
∴a2=bc,
∴这两个盒子的外表面积之差:
S2﹣S1=bc+﹣(a2+)=a2+﹣a2﹣==.
22.解:它们的名称分别为:球体,直六棱柱,圆锥体,正方体,直三棱柱,圆柱体,四棱锥,长方体.
23.解:底面周长是12cm,高6cm时,圆柱的表面积为:12×6+=72+≈96(cm2);
底面周长是6cm,高12cm时,圆柱的表面积为:12×6+=72+≈78(cm2).
24.解:18.84÷3=6.28(分米),
6.28÷3.14÷2=1(分米),
3.14×12×3=9.42(立方分米);
3.14×12×2+18.84=25.12(平方分米).
答:这个圆柱的体积减少了9.42立方分米,要漆25.12平方分米.
25.解:这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
(1)面F会在上面;
(2)面C会在上面;
(3)面A会在上面.
26.解:如图所示,
A旋转后得出图形c,B旋转后得出图形d,C旋转后得出图形a,D旋转后得出图形e,E旋转后得出图形b.
27.解:根据正方体的特征知,相邻的面一定不是对面,
∵面“3”与面“1、2、4、5”相邻,
∴面“3”与面“6”相对,
∵面“2”和面“1、3、4”相邻,
∴面“2”与面“4”或面“5”相对,
面“2”与面“4”相对时,3对6,2对4,1对5;
面“2”与面“5”相对时,3对6,2对5,1对4;
丰富的图形世界》单元测试卷
一.选择题
1.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A.
B.
C.
D.
2.如图是一个正方体的表面展开图,在这个正方体中,与点A重合的点为( )
A.点C和点N
B.点B和点M
C.点C和点M
D.点B和点N
3.下列图形(如图所示)经过折叠不能围成正方体的是( )
A.
B.
C.
D.
4.小刚同学在一个正方体盒子的每个面都写了一个字,分别是:我、喜、欢、数、学、课.其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )
A.课
B.欢
C.数
D.学
5.下面是一个正方体,用一个平面去截这个正方体截面形状不可能为下图中的( )
A.
B.
C.
D.
6.如图,小亮用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图
①变到图②,不改变的是( )
A.主视图
B.主视图和左视图
C.主视图和俯视图
D.左视图和俯视图
7.下列图形,不是柱体的是( )
A.
B.
C.
D.
8.10个棱长为1m的正方体,构成如图所示的形状,然后把露在外面的表面都涂上颜色,那么被涂上颜色的总面积为( )
A.36m2
B.32m2
C.30m2
D.28m2
9.如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( )
A.
B.
C.
D.
10.如图,下列图形从正面看是三角形的是( )
A.
B.
C.
D.
二.填空题
11.五棱柱有
条棱.
12.笔尖在纸上快速滑动写出英文字母C,这说明了
.
13.如图,有三张硬纸片,用它们围成一个立体图形叫
.
14.如图所示,将图沿虚线折起来,得到一个正方体,那么“3”的对面是
(填编号).
15.如图②是圆柱被一个平面斜切后得到的几何体,请类比梯形面积公式的推导方法(如图①),推导图②几何体的体积为
.(结果保留π)
16.写出一个在三视图中俯视图与主视图完全相同的几何体
.
17.如图,在四个小正方体搭成的几何体中,每个小正方体的棱长都是1,则该几何体的三视图的面积之和是
.
18.一个几何体的三视图如图所示,则该几何体的表面积是
.
19.将一个棱长为8、各个面上均涂有颜色的正方体,锯成64个同样大小的小正方体,其中所有恰有2面涂有颜色的小正方体表面积之和为
.
20.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于
.
三.解答题
21.一个无盖长方体盒子的容积是V.
(1)如果盒子底面是边长为a的正方形,这个盒子的表面积是多少?
(2)如果盒子底面是长为b、宽为c的长方形,这个盒子的表面积是多少?
(3)上面两种情况下,如果盒子的底面面积相等.那么两种盒子的表面积相差多少?(不计制造材料的厚度.)
22.观察图中的立体图形,分别写出它们的名称.
23.用长为12厘米、宽为6厘米的长方形纸片围成一个圆柱的侧面(不计损耗),求得到圆柱的表面积.(π取3)
24.一个圆柱体,如果把它的高截短3分米,它的表面积就减少18.84平方分米,这个圆柱的体积减少了多少立方分米?要把截下的高3分米的圆柱部分漆上油漆,要漆多少平方分米?
25.如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
26.将第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
27.一个正方体6个面分别写着1、2、3、4、5、6,根据下列摆放的三种情况,那么每个数对面上的数是几?
参考答案与试题解析
一.选择题
1.解:A、是两个圆台,故A错误;
B、上面小下面大,侧面是曲面,故B正确;
C、是一个圆台,故C错误;
D、下面小上面大侧面是曲面,故D错误;
故选:B.
2.解:折叠成正方体时,与点A重合的点为C、N.
故选:A.
3.解:A、C、D经过折叠均能围成正方体,
B折叠后第一行两个面无法折起来,而且下边没有面,不能折成正方体.
故选:B.
4.解:正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,
所以该正方体盒子上,“我”相对的面上所写的文字是“课”;
故选:A.
5.解:无论如何去截,截面也不可能有弧度,因此截面不可能是圆.
故选:D.
6.解:从左面看第一层都是三个小正方形,第二层左边一个小正方形,①②的左视图相同;
从上面看第一列都是一个小正方形,第二列都是一个小正方形,第三列都是三个小正方形,故①②的俯视图相同,
故选:D.
7.解:长方体是四棱柱,三棱柱是柱体,圆锥是锥体,圆柱是柱体,
故选:D.
8.解:∵要染色的上底面有6个,侧面有24个,
∴被染色的图形的面积是:(24+6)×(1×1)=30(m2),
故选:C.
9.解:从主视图看第一列两个正方体,说明俯视图中的左边一列有两个正方体,主视图右边的一列只有一行,说明俯视图中的右边一列两行都只有一个正方体,所以此几何体如图所示:.
故选:B.
10.解:A、三棱柱从正面看到的是长方形,不合题意;
B、圆台从正面看到的是梯形,不合题意;
C、圆锥从正面看到的是三角形,符合题意;
D、长方体从正面看到的是长方形,不合题意.
故选:C.
二.填空题
11.解:五棱柱有侧棱5条,
底面上的棱5×2=10条,
所以,共有5+10=15条.
故答案为:15.
12.解:笔尖在纸上快速滑动写出英文字母C,这说明了点动成线;
故答案为:点动成线
13.解:利用三视图有关知识,矩形只能组成圆柱形,两个圆正好组成圆柱的上底与下底.
故填:圆柱体
14.解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,
∴在此正方体上与“3”相对的面上的数字是“6”.
故答案为:6.
15.解:π()2×(8﹣6)×+π()2×6,
=9π+54π
=63π.
故答案为:63π.
16.解:球的俯视图与主视图都为圆;
正方体的俯视图与主视图都为正方形.
故答案为:球或正方体(答案不唯一).
17.解:主视图是第一层是三个小正方形,第二层右边一个小正方形,主视图的面积是4,
俯视图是三个小正方形,俯视图的面积是3,
左视图是下边一个小正方形,第二层一个小正方形,左视图的面积是2,
几何体的三视图的面积之和是4+3+2=9,
故答案为:9.
18.解:由三视图可知:原几何体为圆柱的一半,(沿中轴线切开),
由题意可知,圆柱的高为8,底面圆的半径为4,
故其表面积为S=42π+4π×8+8×8=48π+64.
故答案为:48π+64.
19.解:根据以上分析:小正方体的棱长是2,表面积是2×2×6=24,恰有2面涂有颜色的小正方体共有24个.则这样的小正方体表面积的和是24×24=576.
故答案为576.
20.解:①底面周长为6,高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π,高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
三.解答题
21.解:(1)∵一个无盖长方体盒子的容积是V,盒子地面边长为a的正方形,
∴长方体盒子的高为:h=,
∴这个盒子的外表面积S1=a2+×4a=a2+;
(2)∵一个无盖长方体盒子的容积是V,盒子底面是长为b,宽为c的长方形,
∴长方体盒子的高为:h=,
∴这个盒子的外表面积S2=bc+×2(b+c)=bc+;
(3)∵盒子的底面积相等,
∴a2=bc,
∴这两个盒子的外表面积之差:
S2﹣S1=bc+﹣(a2+)=a2+﹣a2﹣==.
22.解:它们的名称分别为:球体,直六棱柱,圆锥体,正方体,直三棱柱,圆柱体,四棱锥,长方体.
23.解:底面周长是12cm,高6cm时,圆柱的表面积为:12×6+=72+≈96(cm2);
底面周长是6cm,高12cm时,圆柱的表面积为:12×6+=72+≈78(cm2).
24.解:18.84÷3=6.28(分米),
6.28÷3.14÷2=1(分米),
3.14×12×3=9.42(立方分米);
3.14×12×2+18.84=25.12(平方分米).
答:这个圆柱的体积减少了9.42立方分米,要漆25.12平方分米.
25.解:这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
(1)面F会在上面;
(2)面C会在上面;
(3)面A会在上面.
26.解:如图所示,
A旋转后得出图形c,B旋转后得出图形d,C旋转后得出图形a,D旋转后得出图形e,E旋转后得出图形b.
27.解:根据正方体的特征知,相邻的面一定不是对面,
∵面“3”与面“1、2、4、5”相邻,
∴面“3”与面“6”相对,
∵面“2”和面“1、3、4”相邻,
∴面“2”与面“4”或面“5”相对,
面“2”与面“4”相对时,3对6,2对4,1对5;
面“2”与面“5”相对时,3对6,2对5,1对4;
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
