上海市闵行区2020-2021学年七年级下学期期末质量调研考试数学试卷(PDF版,附答案)
文档属性
| 名称 | 上海市闵行区2020-2021学年七年级下学期期末质量调研考试数学试卷(PDF版,附答案) |  | |
| 格式 | |||
| 文件大小 | 221.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 23:12:38 | ||
图片预览



文档简介
闵行区 2020 学年第二学期七年级质量监控考试
数 学 试 卷
(考试时间90分钟,满分100分)
考生注意:
1. 本试卷含四个大题, 共27题.
2.
225= ±15; (D) -8
A
D
F G
B C E
(第6题图)
第 1 页 共4页
二、填空题:(本大题共12题,每题2分,满分24分)
7.计算: 0
2= ▲ .
8.比较大小:3 5 ▲ 5 3(填“>”或“<”).
9.点A和点B是数轴上的两点,点A表示的数为 2,点B表示的数为1,那么A、B
两点间的距离为 ▲ .
10.利用计算器计算: 3
4 3? = ▲ (保留两位有效数字).
11.计算: 2 2
6 8? = ▲ .
12.在平面直角坐标系xOy中,已知点A(2,n)在第四象限,点B(m,1)在第二象
限,那么点C(m,n)在第 ▲ 象限.
13.在平面直角坐标系xOy中,已知点A(4,3)向左移动3个单位后得到点B,那么
点B的坐标是 ▲ .
14.已知等腰三角形的两边长分别为1和2,那么这个三角形的周长为 ▲ .
15.在△ABC中,如果AB=AC,∠A=∠C,那么△ABC的形状为 ▲ .
16.如图,已知AB//CD,直线EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD
的平分线与EP相交于点P,且∠BEP=30°,那么∠EFP的度数为 ▲ .
A
A E B
P
E D
C F D O
B C
(第16~v. (第17题图)
17.如图,已知∠B=∠C,从下列条件中选择一个,则可以证明△OEB全等于△ODC.
①AD=AE,②OB=OC,③BD=CE,④∠BEO=∠CDO,那么这个条件可以是 ▲ (写出
所有符合条件的序号).
18.点A位于点B的北偏东方向15°,若将点B以点A为旋转中心旋转90°落在点C
处,则点A在点C的 ▲ 方向.
三、解答题(本大题共8题,满分64分)
19.(本题满分6分)
? ?1
计算:? ?? ?8 2? ? .
? ?2
20.(本题满分6分)
2 2
计算:? ?3 2 3 2? ? ?? ? .
第 2 页 共4页
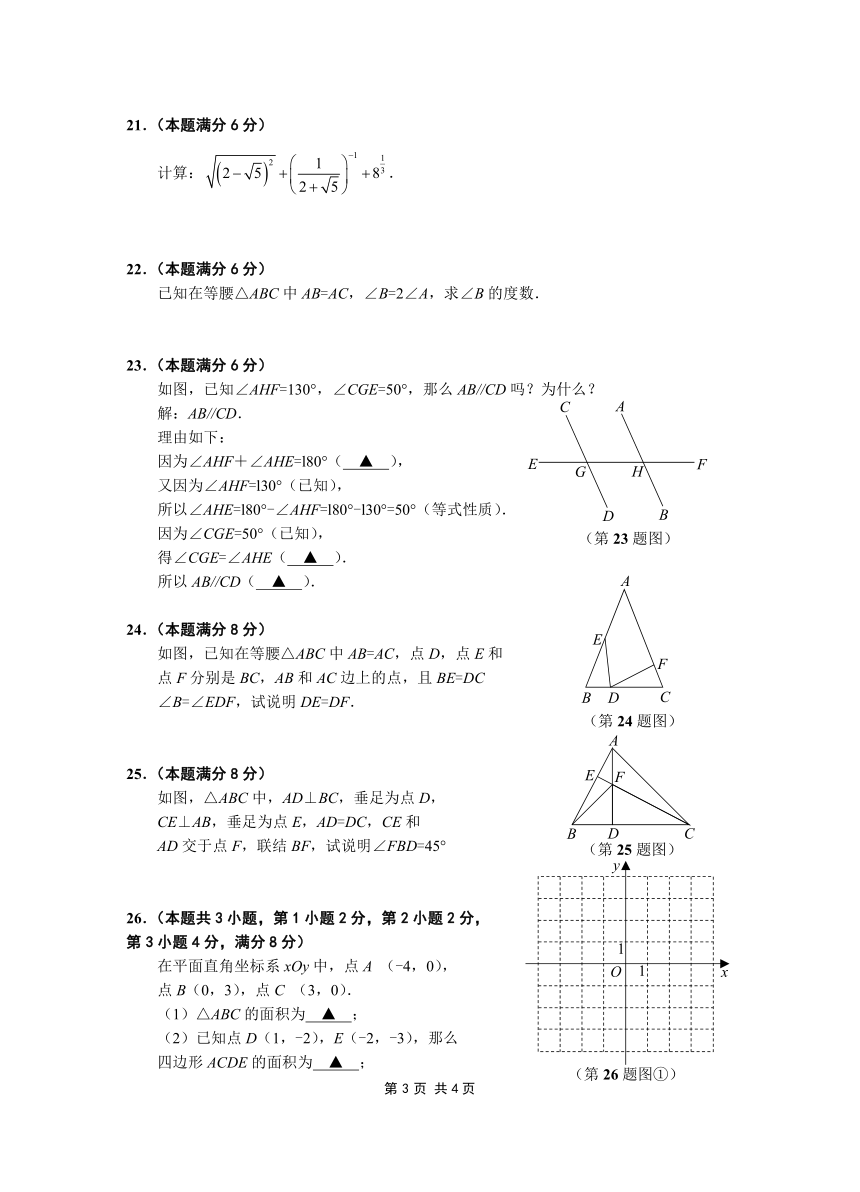
21.(本题满分6分)
2 ?1 1
? ?1
计算: 3
? ?2? 5 ? ?? ? 8 .
?2 5? ?
22.(本题满分6分)
已知在等腰△ABC中AB=AC,∠B=2∠A,求∠B的度数.
23.(本题满分6分)
如图,已知∠AHF=130°,∠CGE=50°,那么AB//CD吗?为什么?
解:AB//CD. C A
理由如下:
因为∠AHF+∠AHE=l80°( ▲ ), E G H F
又因为∠AHF=l30°(已知),
所以∠AHE=l80°-∠AHF=l80°-l30°=50°(等式性质). D B
因为∠CGE=50°(已知), (第23题图)
得∠CGE=∠AHE( ▲ ).
所以AB//CD( ▲ ). A
24.(本题满分8分) E
如图,已知在等腰△ABC中AB=AC,点D,点E和 F
点F分别是BC,AB和AC边上的点,且BE=DC
∠B=∠EDF,试说明DE=DF. B D C
(第24题图)
A
25.(本题满分8分) E F
如图,△ABC中,AD⊥BC,垂足为点D,
CE⊥AB,垂足为点E,AD=DC,CE和 B D C
AD交于点F,联结BF,试说明∠FBD=45° (第25题图)
y
26.(本题共3小题,第1小题2分,第2小题2分,
第3小题4分,满分8分) 1
在平面直角坐标系xOy中,点A (-4,0), O 1 x
点B(0,3),点C (3,0).
(1)△ABC的面积为 ▲ ;
(2)已知点D(1,-2),E(-2,-3),那么
四边形ACDE的面积为 ▲ ;
(第26~v①)
第 3 页 共4页
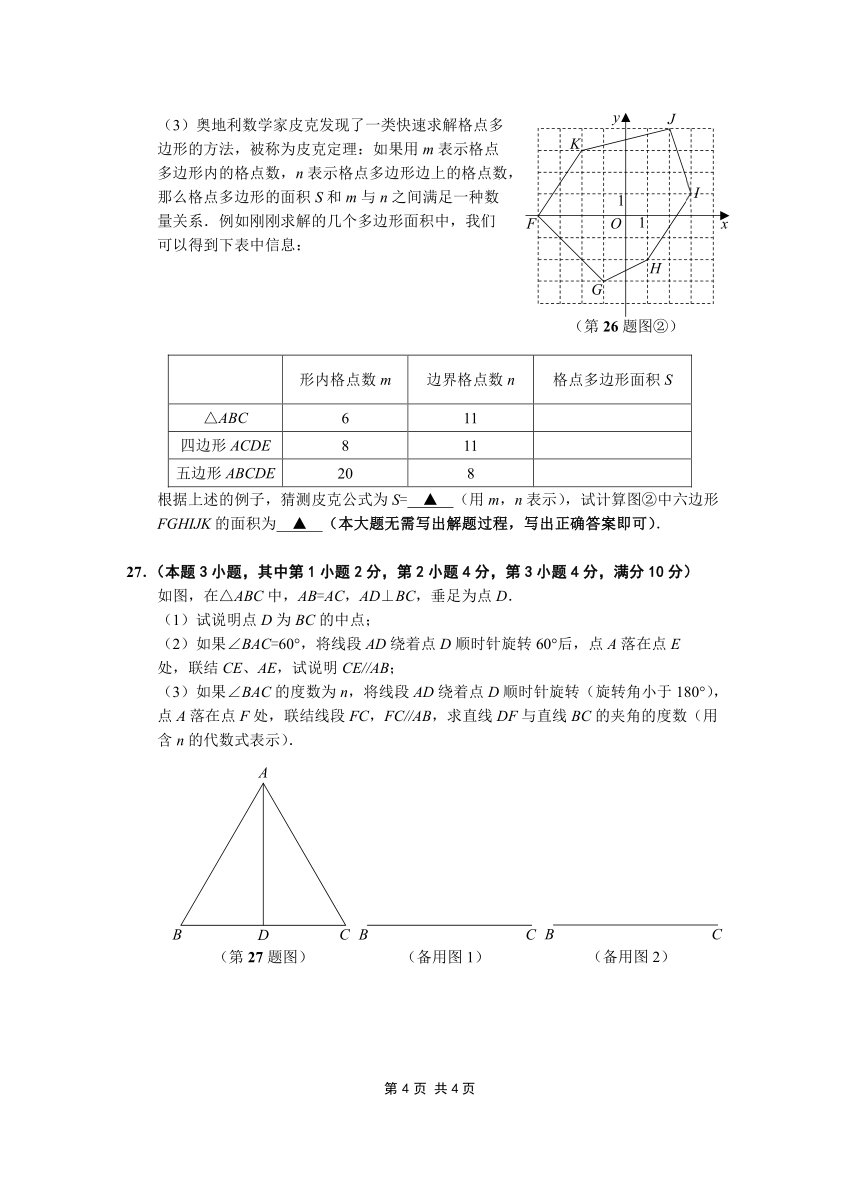
(3)奥地利数学家皮克发现了一类快速求解格点多 y J
边形的方法,被称为皮克定理:如果用m表示格点 K
多边形内的格点数,n表示格点多边形边上的格点数,
那么格点多边形的面积S和m与n之间满足一种数 1 I
量关系.例如刚刚求解的几个多边形面积中,我们 F O 1 x
可以得到下表中信息:
H
G
(第26~v②)
形内格点数m 边界格点数n 格点多边形面积S
△ABC 6 11
四边形ACDE 8 11
五边形ABCDE 20 8
根据上述的例子,猜测皮克公式为S= ▲ (用m,n表示),试计算图②中六边形
FGHIJK的面积为 ▲ (本大题无需写出解题过程,写出正确答案即可).
27.(本题3小题,其中第1小题2分,第2小题4分,第3小题4分,满分10分)
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D.
(1)试说明点D为BC的中点;
(2)如果∠BAC=60°,将线段AD绕着点D顺时针旋转60°后,点A落在点E
处,联结CE、AE,试说明CE//AB;
(3)如果∠BAC的度数为n,将线段AD绕着点D顺时针旋转(旋转角小于180°),
点A落在点F处,联结线段FC,FC//AB,求直线DF与直线BC的夹角的度数(用
含n的代数式表示).
A
B D C B C B C
(第27~v. (备用图1. (备用图2.
第 4 页 共4页
闵行区 2020 学年第二学期七年级质量监控考试
数 学 答题纸
注 意 事 项 学校 %& '(
1.答题前,考生先将自己的姓名、 )*+
#$?)*+@ABCD/0)*E
F,-.G
2.选择题部分必须使用2B铅笔填
涂;非选择题部分使用黑色字迹的
钢笔、圆珠笔或签字笔书写,字体工
整、笔迹清楚.
3.请按照题号顺序在各题目的答题 条形码粘贴处
区域内作答,超出答题区域书写的
答案无效;在草稿纸、试题卷上答题
无效.
4.保持卡面清洁,不折叠,不破损.
一、选择题
1. [A] [B] [C] [D] 2. [A] [B] [C] [D] 3. [A] [B] [C] [D]
4. [A] [B] [C] [D] 5. [A] [B] [C] [D] 6. [A] [B] [C] [D]
二、填空题
7. 8. 9.
10. 11. 12.
13. 14. 15.
16. 17. 18.
三、解答题
19.解:
第 5 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效
20.解:
21.解:
22.解:
第 6 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效
23.解:AB//CD.
理由如下:
因为∠AHF+∠AHE=l80°( ),
又因为∠AHF=l30°(已知), C A
所以∠AHE=l80°-∠AHF=l80°-l30°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE( ). E G H F
所以AB//CD( ).
D B
(第23题图)
24.解:
A
E
F
B D C
(第24题图)
第 7 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效 不
25.解:
A 许
E F 折
B D C
(第25题图) 叠
请
在
各
题
目
的
答
题
26.(1)△ABC的面积为 ; y 区
(2)四边形ACDE的面积为 ; 域
(3)皮克公式为S= ,六边形FGHIJK的面积为 . 内
作
1
答
O 1 x
,
超
出
黑
(第26~v①) 色
矩
形
边
框
限
定
区
域
的
答
第 8 页 共4页 案
无
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效 效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效
27.解:(1) A
( B C
2) D
(第27~v.
B C
(备用图1.
(3)
B C
(备用图2.
第 9 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
闵行区 2020 学年第二学期七年级质量监控考试数学试卷
参考答案及评分标准
一、选择题:(本大题共6题,每题2分,满分12分)
1.A
解析:通过数轴的概念即可解答.
2.C
解析:C项中应只有平行直线被第三条直线所载,同位角才相等,A、B、D项正确,故选C.
3.C
解析:本题主要考查方根的概念,C项中 225指225的算术平方根,应该等于15,A、B、D项正确,故
选C.
4.D
解析:本题主要考查平面直角坐标系相关概念,由点A与点B关于x轴对称可知,点A与点B的纵坐标互
为相反数,故选D.
5.B
解析:本题主要考查全等三角形的判定,A项的判定方法为S.S.S,正确,B项的判断方法为S.S.A,不能判定
两三角形全等,错误,C项的判定方法为S.A.S,正确,D项的判定方法为A.A.S,正确,故选B.
6.B
解析:本题主要考查等边三角形与全等三角形有关概念,A项可由AC=BC,∠ACE=∠BCD,CE=CD得
△ACE≌△BCD得到,C、D项可由∠ECG=∠FCD,CE=CD,∠CEG=∠CDF得△CEG≌△CDF得到,
而B项不能由已知条件得到,故选B.
二、填空题:(本大题共12题,每题2分,满分24分)
7.1
解析:通过“任意非零数的零次幂为1”即可解答.
8.<
解析:本题主要考查无理数的比较,3 5= 45,5 3= 75, 45< 75,所以3 5<5 3.
9. 2 1?
解析:本题主要考查数轴上两点间的距离,点A和点B间的距离是| 2 1? |= 2 1? .
10.0.56
解析:利用计算器可算出 4 3?3 ≈ 0.557750429692591617678361689219041160813074650064942245358380
545831124031700026601452445202943547433131649191455104500335745760538897402851310498428147627
729096679761524015549389144599727399118545011272486326446475321339252843115607766810817982961
0017617766787,第一位0不是有效数字,其从左至右第三个有效数字是7,所以四舍五入得0.56.
11.10
11.解析:62=36,82=64,36+64=100, 100=10.
12.三
解析:本题主要考查直角坐标平面中点的象限的判定,由题意可知m<0,n<0,所以点C在第三象限.
13.(1,3)
解析:本题主要考查直角坐标平面中点的移动,点A向左移动3个单位,即点A的横坐标减3,所以点B的
坐标是(1,3).
14.5
解析:本题主要考查三角形的三边关系,题中等腰三角形的三边长有两种情况:2、2、1或1、1、2,后一种
不符合三角形的三边关系,舍去,所以三角形周长为2+2+1=5.
15.等边三角形
解析:本题主要考查“等边对等角”及等边三角形判定,在△ABC中,由AB=AC得∠B=∠C,又因为
∠A=∠C,所以∠A=∠B=∠C,得△ABC是等边三角形.
16.30°
解析:本题主要考查平行线的性质,由∠BEP=30°,EP⊥EF,得∠BEF=∠BEP+∠FEP=120°,由
AB//CD得∠BEF+∠DFE=180°,所以∠DFE=60°,由EP平分∠DFE得∠EFP=30°.
17.①或②或③
解析:选择①和②均可与∠B=∠C一起得到△ABD≌△ACE,得AB=AC,AD=AE,进而得到BE=CD,
第 10 页 共4页
再与∠B=∠C一起得到△OEB≌△ODC,选择③可直接与∠B=∠C一起得到△OEB≌△ODC,选择④
择没有已知的边,不能得到△OEB≌△ODC.
18.北偏西75°或南偏东75°
解析:本题主要考查旋转与方向,题目中的旋转有两种可能:顺时针旋转与逆时针旋转,若是顺时针旋转,
则点A在点C的南偏东90°-15°=75°方向,若是逆时针旋转,则点A在点C的北偏西90°-15°=75°方
向,可以画图帮助理解.
三、解答题(本大题共8题,满分64分)
1
19.解:原式= 8 2 2? ? ? ……………………………………………………(2分)
2
1
= 4?
4
1
=2? ……………………………………………………………………(2分)
2
5
= …………………………………………………………………………(2分)
2
解析:本题主要考查乘法分配律,解题过程如上.
20.解:原式=? 3 2 3 2 3 2 3 2? ? ? ? ? ? ?? ? ? …………………………(2分)
=2 2 2 3? ………………………………………………………………(2分)
=4 6 ……………………………………………………………………(2分)
解析:本题主要考查平方差公式运用,解题过程如上.
1
3
21.解:原式= 2 5 2 5 2? ? ? ? 3
? ? ? ?
= 5 2 2 5 2? ? ? ? ……………………………………………………(4分)
=2 2 5? …………………………………………………………………(2分)
解析:解题过程如上.
22.解:因为AB=AC(已知),
所以∠B=∠C(等边对等角). ………………………………………………(2分)
因为∠B=2∠A(已知),
1
所以∠A= ∠B(等式性质).
2
因为∠A+∠B+∠C=180°(三角形的内角和等于180°),
1
所以 ∠B+∠B+∠B=180°(等式性质), …………………………………(2分)
2
5
所以 ∠B=180°(等式性质),
2
所以∠B=72°(等式性质). …………………………………………………(2分)
解析:本题主要考查三角形的内角和,利用三角形内角和与已知条件列出方程即可解答,解题过
程如上.
23.解:AB//CD.
理由如下:
因为∠AHF+∠AHE=l80°(邻补角的意义), ………………………………(2分)
又因为∠AHF=l30°(已知),
所以∠AHE=l80°-∠AHF=l80°-l30°=50°(等式性质).
因为∠CGE=50°(已知),
第 11 页 共4页
得∠CGE=∠AHE(等量代换). ……………………………………………(2分)
所以AB//CD(同位角相等,两直线平行). ………………………………(2分)
解析:第一空∠AHF与∠AHE互为邻补角,这里利用邻补角互补的性质,所以填“邻补角的意义”,第二
空∠CGE与∠AHE都等于50°,所以填“等量代换”,第三空∠CGE与∠AHE为相等的同位角,由此
得AB//CD,所以填“同位角相等,两直线平行”.
24.解:因为AB=AC(已知),
所以∠B=∠C(等边对等角). ………………………………………………(2分)
因为∠B+∠BED=∠CDE(三角形的一个外角等于与它不相邻的两个内角的和),
∠EDF+∠CDF=∠CDE(已知),
所以∠B+∠BED=∠EDF+∠CDF(等量代换). ……………………………(1分)
因为∠B=∠EDF(已知),
所以∠BED=∠CDF(等式性质). …………………………………………(1分)
在△BDE与△CFD中,
?? ? ?B C(已证),
??B DCE ? (已知),
??? ? ?BED CDF(已证),
所以△BDE≌△CFD(A.S.A), ……………………………………………(1分)
所以DE=DF(全等三角形的对应边相等). ………………………………(1分)
解析:本题主要考查三角形外角性质与三角形全等,解题过程如上.
25.解:因为AD⊥BC,CE⊥AB(已知),
所以∠AOB=90°,∠ADC=90°,∠BEC=90°(垂直的意义),
所以∠AOB=∠ADC=∠BEC(等量代换). …………………………………(2分)
因为∠BEC=∠EAF+∠AFE,∠ADB=∠DCF+∠CFD
(三角形的一个外角等于与它不相邻的两个内角的和),
所以∠EAF+∠AFE=∠DCF+∠CFD(等量代换).
因为∠AFE=∠CFD(对顶角相等),
所以∠EAF=∠DCF(等式性质). …………………………………………(2分)
在△ABD与△CFD中,
?? ? ?BAD DCF(已证),
??AD DC? (已知),
??? ? ?ADB CDF(已证),
所以△ABD≌△CFD(A.S.A), ……………………………………………(1分)
所以BD=FD(全等三角形的对应边相等),
所以∠DBF=∠BFD(等边对等角). ………………………………………(1分)
因为∠ADC=∠DBF+∠BFD
(三角形的一个外角等于与它不相邻的两个内角的和),
所以∠DBF+∠BFD=90°(等量代换),
所以∠FBD=45°(等式性质). ………………………………………………(2分)
解析:本题主要考查全等三角形与等腰直角三角形的概念,解题过程如上.
26.(1)10.5
解析:△ABC的底为7,高为3,所以面积为0.5×7×3=10.5.
(2)12.5
解析:四边形ACDE的面积可以通过多种方法求出,以下为其中一种:S=0.5×2×3+3×2+0.5×3×1
+0.5×2×2=3+6+1.5+2=12.5.
n
(3)皮克公式为S=m? ?1,六边形FGHIJK的面积为30.
2
解析:第一空通过表中信息即可解答,第二空六边形FGHIJK的形内格点数m为27,边界格点数n
为8,根据皮克公式即可求解.
27.(1)解:因为AB=AC,AD⊥BC(已知),
第 12 页 共4页
所以点D为BC的中点.
(等腰三角形底边上的中线与底边上的高互相重合) …………(2分)
解析:本题主要考查等腰三角形的三线合一性质,利用“等腰三角形底边上的中线与底边上的高互相
重合”即可解答,解题过程如上.
(2)解:因为AB=AC,∠BAC=60°(已知),
所以△ABC是等边三角形
(有一个内角等于60°的等腰三角形是等边三角形),
所以∠B=∠ACB=60°(等边三角形的三内角等于60°).
因为AD⊥BC(已知),
1
所以∠CAD= ∠BAC
2
(等腰三角形底边上的中线与顶角的平分线互相重合),
所以∠CAD=30°(等式性质).
因为AD=DE,∠ADE=60°(旋转的意义),
所以△ADE是等边三角形
(有一个内角等于60°的等腰三角形是等边三角形),
所以AD=AE(等边三角形的三边相等),
∠DAE=60°(等边三角形的三内角等于60°). …………………(1分)
所以∠DAE-∠CAD=30°(等式性质),
即∠CAE=30°,
所以∠CAD=∠CAE(等量代换). ……………………………………(1分)
在△ACD与△ACE中,
?AC AC? (公共边),
??? ? ?CAD CAE(已证),
??AD AE? (已证),
所以△ACD≌△ACE(S.A.S). ………………………………………(1分)
所以∠ACD=∠ACE(全等三角形的对应边相等),
所以∠ACE=60°(等量代换),
所以∠ACD+∠ACE=120°(等式性质),
即∠DCE=120°,
所以∠B+∠DCE=180°(等式性质),
所以CE//AB(同旁内角互补,两直线平行). ………………………(1分)
解析:本题主要考查等边三角形与全等三角形有关概念,解题过程如上.
(3)解:因为AB=AC(已知),
所以∠ABC=∠ACB(等边对等角),
因为∠BAC=n(已知),
∠BAC+∠ABC+∠ACB=180°(三角形的内角和等于180°),
所以∠ABC+∠ACB=180°-n(等式性质),
1
所以∠ABC=∠ACB=90? ? n(等式性质).
2
因为AD⊥BC(已知),
所以BD=CD(等腰三角形底边上的中线与底边上的高互相重合),
1
∠BAD= ∠BAC(等腰三角形底边上的中线与顶角的平分线互相重合).
2
当∠BAC的度数为n,n有三种可能情况:n<90°,n>90°,n=90°.
(i) 当n<90°时:
延长AB、FD交于点G.
因为FC//AB(已知),
所以∠CBG=∠BCF(两直线平行,内错角相等),
第 13 页 共4页
∠ABC+∠BCF=180°(两直线平行,同旁内角互补),
1
所以∠BCF=90? ? n(等式性质),
2
1
所以∠CBG=90? ? n(等量代换).
2
在△BDG与△CDF中,
?? ? ?DBG DCF(已证),
??BD CD? (已证),
??? ? ?BDG CDF(对顶角相等),
所以△BDG≌△CDF(A.S.A),
所以DG=DF(全等三角形的对应边相等),
∠G=∠F(全等三角形的对应角相等).
因为AD=DF(旋转的意义),
所以DG=AD(等量代换),
所以∠BAD=∠G(等边对等角),
1
所以∠G= n(等量代换).
2
因为∠BAC=∠G+∠BDG
(三角形的一个外角等于与它不相邻的两个内角的和),
1 1
所以∠BDG=90? ? ?n n(等式性质),
2 2
所以∠BDG=90°-n(等式性质).
因为∠CDF=∠BDG(对顶角相等),
所以∠CDF=90°-n(等量代换),
所以直线DF与直线BC的夹角的度数是90°-n. …………(1分)
(ii)当n>90时:
延长FD交AB于点G.
因为FC//AB(已知),
所以∠CBG=∠BCF(两直线平行,内错角相等).
在△BDG与△CDF中,
?? ? ?DBG DCF(已证),
??BD CD? (已证),
??? ? ?BDG CDF(对顶角相等),
所以△BDG≌△CDF(A.S.A),
所以DG=DF(全等三角形的对应边相等),
∠B=∠DCF(全等三角形的对应角相等).
因为AD=DF(旋转的意义),
所以DG=AD(等量代换),
所以∠DAG=∠AGD(等边对等角),
1
所以∠AGD= n(等量代换).
2
因为∠AGD=∠B+∠BDG
(三角形的一个外角等于与它不相邻的两个内角的和),
1 1
所以∠BDG= n n? ? ?90 (等式性质),
2 2
所以∠BDG=n-90°(等式性质).
第 14 页 共4页
因为∠CDF=∠BDG(对顶角相等),
所以∠CDF=90°-n(等量代换),
所以直线DF与直线BC的夹角的度数是n-90°. …………(1分)
(iii)当n=90°时:
因为n=90°(已知),
所以∠ACD=45°,∠DAC=45°(等式性质),
所以∠ACD=∠DAC(等量代换),
所以AD=CD(等边对等角),
因为AD=DF(旋转的意义),
所以CD=DF(等量代换),
所以点C与点F重合,
即∠CDF=0°,
所以不符合题意,舍去. ………………………………………(1分)
所以直线DF与直线BC的夹角的度数是90°-n或n-90°. …………(1分)
解析:本题主要考查平行线、等腰三角形与全等三角形的有关概念,辅助线的添加、方程思想,以及
问题的多样性,解题过程中要注意考虑完整,正确添加辅助线,解题过程如上.
第 15 页 共4页
数 学 试 卷
(考试时间90分钟,满分100分)
考生注意:
1. 本试卷含四个大题, 共27题.
2.
225= ±15; (D) -8
A
D
F G
B C E
(第6题图)
第 1 页 共4页
二、填空题:(本大题共12题,每题2分,满分24分)
7.计算: 0
2= ▲ .
8.比较大小:3 5 ▲ 5 3(填“>”或“<”).
9.点A和点B是数轴上的两点,点A表示的数为 2,点B表示的数为1,那么A、B
两点间的距离为 ▲ .
10.利用计算器计算: 3
4 3? = ▲ (保留两位有效数字).
11.计算: 2 2
6 8? = ▲ .
12.在平面直角坐标系xOy中,已知点A(2,n)在第四象限,点B(m,1)在第二象
限,那么点C(m,n)在第 ▲ 象限.
13.在平面直角坐标系xOy中,已知点A(4,3)向左移动3个单位后得到点B,那么
点B的坐标是 ▲ .
14.已知等腰三角形的两边长分别为1和2,那么这个三角形的周长为 ▲ .
15.在△ABC中,如果AB=AC,∠A=∠C,那么△ABC的形状为 ▲ .
16.如图,已知AB//CD,直线EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD
的平分线与EP相交于点P,且∠BEP=30°,那么∠EFP的度数为 ▲ .
A
A E B
P
E D
C F D O
B C
(第16~v. (第17题图)
17.如图,已知∠B=∠C,从下列条件中选择一个,则可以证明△OEB全等于△ODC.
①AD=AE,②OB=OC,③BD=CE,④∠BEO=∠CDO,那么这个条件可以是 ▲ (写出
所有符合条件的序号).
18.点A位于点B的北偏东方向15°,若将点B以点A为旋转中心旋转90°落在点C
处,则点A在点C的 ▲ 方向.
三、解答题(本大题共8题,满分64分)
19.(本题满分6分)
? ?1
计算:? ?? ?8 2? ? .
? ?2
20.(本题满分6分)
2 2
计算:? ?3 2 3 2? ? ?? ? .
第 2 页 共4页
21.(本题满分6分)
2 ?1 1
? ?1
计算: 3
? ?2? 5 ? ?? ? 8 .
?2 5? ?
22.(本题满分6分)
已知在等腰△ABC中AB=AC,∠B=2∠A,求∠B的度数.
23.(本题满分6分)
如图,已知∠AHF=130°,∠CGE=50°,那么AB//CD吗?为什么?
解:AB//CD. C A
理由如下:
因为∠AHF+∠AHE=l80°( ▲ ), E G H F
又因为∠AHF=l30°(已知),
所以∠AHE=l80°-∠AHF=l80°-l30°=50°(等式性质). D B
因为∠CGE=50°(已知), (第23题图)
得∠CGE=∠AHE( ▲ ).
所以AB//CD( ▲ ). A
24.(本题满分8分) E
如图,已知在等腰△ABC中AB=AC,点D,点E和 F
点F分别是BC,AB和AC边上的点,且BE=DC
∠B=∠EDF,试说明DE=DF. B D C
(第24题图)
A
25.(本题满分8分) E F
如图,△ABC中,AD⊥BC,垂足为点D,
CE⊥AB,垂足为点E,AD=DC,CE和 B D C
AD交于点F,联结BF,试说明∠FBD=45° (第25题图)
y
26.(本题共3小题,第1小题2分,第2小题2分,
第3小题4分,满分8分) 1
在平面直角坐标系xOy中,点A (-4,0), O 1 x
点B(0,3),点C (3,0).
(1)△ABC的面积为 ▲ ;
(2)已知点D(1,-2),E(-2,-3),那么
四边形ACDE的面积为 ▲ ;
(第26~v①)
第 3 页 共4页
(3)奥地利数学家皮克发现了一类快速求解格点多 y J
边形的方法,被称为皮克定理:如果用m表示格点 K
多边形内的格点数,n表示格点多边形边上的格点数,
那么格点多边形的面积S和m与n之间满足一种数 1 I
量关系.例如刚刚求解的几个多边形面积中,我们 F O 1 x
可以得到下表中信息:
H
G
(第26~v②)
形内格点数m 边界格点数n 格点多边形面积S
△ABC 6 11
四边形ACDE 8 11
五边形ABCDE 20 8
根据上述的例子,猜测皮克公式为S= ▲ (用m,n表示),试计算图②中六边形
FGHIJK的面积为 ▲ (本大题无需写出解题过程,写出正确答案即可).
27.(本题3小题,其中第1小题2分,第2小题4分,第3小题4分,满分10分)
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D.
(1)试说明点D为BC的中点;
(2)如果∠BAC=60°,将线段AD绕着点D顺时针旋转60°后,点A落在点E
处,联结CE、AE,试说明CE//AB;
(3)如果∠BAC的度数为n,将线段AD绕着点D顺时针旋转(旋转角小于180°),
点A落在点F处,联结线段FC,FC//AB,求直线DF与直线BC的夹角的度数(用
含n的代数式表示).
A
B D C B C B C
(第27~v. (备用图1. (备用图2.
第 4 页 共4页
闵行区 2020 学年第二学期七年级质量监控考试
数 学 答题纸
注 意 事 项 学校 %& '(
1.答题前,考生先将自己的姓名、 )*+
#$?)*+@ABCD/0)*E
F,-.G
2.选择题部分必须使用2B铅笔填
涂;非选择题部分使用黑色字迹的
钢笔、圆珠笔或签字笔书写,字体工
整、笔迹清楚.
3.请按照题号顺序在各题目的答题 条形码粘贴处
区域内作答,超出答题区域书写的
答案无效;在草稿纸、试题卷上答题
无效.
4.保持卡面清洁,不折叠,不破损.
一、选择题
1. [A] [B] [C] [D] 2. [A] [B] [C] [D] 3. [A] [B] [C] [D]
4. [A] [B] [C] [D] 5. [A] [B] [C] [D] 6. [A] [B] [C] [D]
二、填空题
7. 8. 9.
10. 11. 12.
13. 14. 15.
16. 17. 18.
三、解答题
19.解:
第 5 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效
20.解:
21.解:
22.解:
第 6 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效
23.解:AB//CD.
理由如下:
因为∠AHF+∠AHE=l80°( ),
又因为∠AHF=l30°(已知), C A
所以∠AHE=l80°-∠AHF=l80°-l30°=50°(等式性质).
因为∠CGE=50°(已知),
得∠CGE=∠AHE( ). E G H F
所以AB//CD( ).
D B
(第23题图)
24.解:
A
E
F
B D C
(第24题图)
第 7 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效 不
25.解:
A 许
E F 折
B D C
(第25题图) 叠
请
在
各
题
目
的
答
题
26.(1)△ABC的面积为 ; y 区
(2)四边形ACDE的面积为 ; 域
(3)皮克公式为S= ,六边形FGHIJK的面积为 . 内
作
1
答
O 1 x
,
超
出
黑
(第26~v①) 色
矩
形
边
框
限
定
区
域
的
答
第 8 页 共4页 案
无
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效 效
请在各题的答题区域内作答,超出黑色矩形边框限定区域的答案无效
27.解:(1) A
( B C
2) D
(第27~v.
B C
(备用图1.
(3)
B C
(备用图2.
第 9 页 共4页
请在各题的答题区域内作答,超出黑色 矩形边框限定区域的答案无效
闵行区 2020 学年第二学期七年级质量监控考试数学试卷
参考答案及评分标准
一、选择题:(本大题共6题,每题2分,满分12分)
1.A
解析:通过数轴的概念即可解答.
2.C
解析:C项中应只有平行直线被第三条直线所载,同位角才相等,A、B、D项正确,故选C.
3.C
解析:本题主要考查方根的概念,C项中 225指225的算术平方根,应该等于15,A、B、D项正确,故
选C.
4.D
解析:本题主要考查平面直角坐标系相关概念,由点A与点B关于x轴对称可知,点A与点B的纵坐标互
为相反数,故选D.
5.B
解析:本题主要考查全等三角形的判定,A项的判定方法为S.S.S,正确,B项的判断方法为S.S.A,不能判定
两三角形全等,错误,C项的判定方法为S.A.S,正确,D项的判定方法为A.A.S,正确,故选B.
6.B
解析:本题主要考查等边三角形与全等三角形有关概念,A项可由AC=BC,∠ACE=∠BCD,CE=CD得
△ACE≌△BCD得到,C、D项可由∠ECG=∠FCD,CE=CD,∠CEG=∠CDF得△CEG≌△CDF得到,
而B项不能由已知条件得到,故选B.
二、填空题:(本大题共12题,每题2分,满分24分)
7.1
解析:通过“任意非零数的零次幂为1”即可解答.
8.<
解析:本题主要考查无理数的比较,3 5= 45,5 3= 75, 45< 75,所以3 5<5 3.
9. 2 1?
解析:本题主要考查数轴上两点间的距离,点A和点B间的距离是| 2 1? |= 2 1? .
10.0.56
解析:利用计算器可算出 4 3?3 ≈ 0.557750429692591617678361689219041160813074650064942245358380
545831124031700026601452445202943547433131649191455104500335745760538897402851310498428147627
729096679761524015549389144599727399118545011272486326446475321339252843115607766810817982961
0017617766787,第一位0不是有效数字,其从左至右第三个有效数字是7,所以四舍五入得0.56.
11.10
11.解析:62=36,82=64,36+64=100, 100=10.
12.三
解析:本题主要考查直角坐标平面中点的象限的判定,由题意可知m<0,n<0,所以点C在第三象限.
13.(1,3)
解析:本题主要考查直角坐标平面中点的移动,点A向左移动3个单位,即点A的横坐标减3,所以点B的
坐标是(1,3).
14.5
解析:本题主要考查三角形的三边关系,题中等腰三角形的三边长有两种情况:2、2、1或1、1、2,后一种
不符合三角形的三边关系,舍去,所以三角形周长为2+2+1=5.
15.等边三角形
解析:本题主要考查“等边对等角”及等边三角形判定,在△ABC中,由AB=AC得∠B=∠C,又因为
∠A=∠C,所以∠A=∠B=∠C,得△ABC是等边三角形.
16.30°
解析:本题主要考查平行线的性质,由∠BEP=30°,EP⊥EF,得∠BEF=∠BEP+∠FEP=120°,由
AB//CD得∠BEF+∠DFE=180°,所以∠DFE=60°,由EP平分∠DFE得∠EFP=30°.
17.①或②或③
解析:选择①和②均可与∠B=∠C一起得到△ABD≌△ACE,得AB=AC,AD=AE,进而得到BE=CD,
第 10 页 共4页
再与∠B=∠C一起得到△OEB≌△ODC,选择③可直接与∠B=∠C一起得到△OEB≌△ODC,选择④
择没有已知的边,不能得到△OEB≌△ODC.
18.北偏西75°或南偏东75°
解析:本题主要考查旋转与方向,题目中的旋转有两种可能:顺时针旋转与逆时针旋转,若是顺时针旋转,
则点A在点C的南偏东90°-15°=75°方向,若是逆时针旋转,则点A在点C的北偏西90°-15°=75°方
向,可以画图帮助理解.
三、解答题(本大题共8题,满分64分)
1
19.解:原式= 8 2 2? ? ? ……………………………………………………(2分)
2
1
= 4?
4
1
=2? ……………………………………………………………………(2分)
2
5
= …………………………………………………………………………(2分)
2
解析:本题主要考查乘法分配律,解题过程如上.
20.解:原式=? 3 2 3 2 3 2 3 2? ? ? ? ? ? ?? ? ? …………………………(2分)
=2 2 2 3? ………………………………………………………………(2分)
=4 6 ……………………………………………………………………(2分)
解析:本题主要考查平方差公式运用,解题过程如上.
1
3
21.解:原式= 2 5 2 5 2? ? ? ? 3
? ? ? ?
= 5 2 2 5 2? ? ? ? ……………………………………………………(4分)
=2 2 5? …………………………………………………………………(2分)
解析:解题过程如上.
22.解:因为AB=AC(已知),
所以∠B=∠C(等边对等角). ………………………………………………(2分)
因为∠B=2∠A(已知),
1
所以∠A= ∠B(等式性质).
2
因为∠A+∠B+∠C=180°(三角形的内角和等于180°),
1
所以 ∠B+∠B+∠B=180°(等式性质), …………………………………(2分)
2
5
所以 ∠B=180°(等式性质),
2
所以∠B=72°(等式性质). …………………………………………………(2分)
解析:本题主要考查三角形的内角和,利用三角形内角和与已知条件列出方程即可解答,解题过
程如上.
23.解:AB//CD.
理由如下:
因为∠AHF+∠AHE=l80°(邻补角的意义), ………………………………(2分)
又因为∠AHF=l30°(已知),
所以∠AHE=l80°-∠AHF=l80°-l30°=50°(等式性质).
因为∠CGE=50°(已知),
第 11 页 共4页
得∠CGE=∠AHE(等量代换). ……………………………………………(2分)
所以AB//CD(同位角相等,两直线平行). ………………………………(2分)
解析:第一空∠AHF与∠AHE互为邻补角,这里利用邻补角互补的性质,所以填“邻补角的意义”,第二
空∠CGE与∠AHE都等于50°,所以填“等量代换”,第三空∠CGE与∠AHE为相等的同位角,由此
得AB//CD,所以填“同位角相等,两直线平行”.
24.解:因为AB=AC(已知),
所以∠B=∠C(等边对等角). ………………………………………………(2分)
因为∠B+∠BED=∠CDE(三角形的一个外角等于与它不相邻的两个内角的和),
∠EDF+∠CDF=∠CDE(已知),
所以∠B+∠BED=∠EDF+∠CDF(等量代换). ……………………………(1分)
因为∠B=∠EDF(已知),
所以∠BED=∠CDF(等式性质). …………………………………………(1分)
在△BDE与△CFD中,
?? ? ?B C(已证),
??B DCE ? (已知),
??? ? ?BED CDF(已证),
所以△BDE≌△CFD(A.S.A), ……………………………………………(1分)
所以DE=DF(全等三角形的对应边相等). ………………………………(1分)
解析:本题主要考查三角形外角性质与三角形全等,解题过程如上.
25.解:因为AD⊥BC,CE⊥AB(已知),
所以∠AOB=90°,∠ADC=90°,∠BEC=90°(垂直的意义),
所以∠AOB=∠ADC=∠BEC(等量代换). …………………………………(2分)
因为∠BEC=∠EAF+∠AFE,∠ADB=∠DCF+∠CFD
(三角形的一个外角等于与它不相邻的两个内角的和),
所以∠EAF+∠AFE=∠DCF+∠CFD(等量代换).
因为∠AFE=∠CFD(对顶角相等),
所以∠EAF=∠DCF(等式性质). …………………………………………(2分)
在△ABD与△CFD中,
?? ? ?BAD DCF(已证),
??AD DC? (已知),
??? ? ?ADB CDF(已证),
所以△ABD≌△CFD(A.S.A), ……………………………………………(1分)
所以BD=FD(全等三角形的对应边相等),
所以∠DBF=∠BFD(等边对等角). ………………………………………(1分)
因为∠ADC=∠DBF+∠BFD
(三角形的一个外角等于与它不相邻的两个内角的和),
所以∠DBF+∠BFD=90°(等量代换),
所以∠FBD=45°(等式性质). ………………………………………………(2分)
解析:本题主要考查全等三角形与等腰直角三角形的概念,解题过程如上.
26.(1)10.5
解析:△ABC的底为7,高为3,所以面积为0.5×7×3=10.5.
(2)12.5
解析:四边形ACDE的面积可以通过多种方法求出,以下为其中一种:S=0.5×2×3+3×2+0.5×3×1
+0.5×2×2=3+6+1.5+2=12.5.
n
(3)皮克公式为S=m? ?1,六边形FGHIJK的面积为30.
2
解析:第一空通过表中信息即可解答,第二空六边形FGHIJK的形内格点数m为27,边界格点数n
为8,根据皮克公式即可求解.
27.(1)解:因为AB=AC,AD⊥BC(已知),
第 12 页 共4页
所以点D为BC的中点.
(等腰三角形底边上的中线与底边上的高互相重合) …………(2分)
解析:本题主要考查等腰三角形的三线合一性质,利用“等腰三角形底边上的中线与底边上的高互相
重合”即可解答,解题过程如上.
(2)解:因为AB=AC,∠BAC=60°(已知),
所以△ABC是等边三角形
(有一个内角等于60°的等腰三角形是等边三角形),
所以∠B=∠ACB=60°(等边三角形的三内角等于60°).
因为AD⊥BC(已知),
1
所以∠CAD= ∠BAC
2
(等腰三角形底边上的中线与顶角的平分线互相重合),
所以∠CAD=30°(等式性质).
因为AD=DE,∠ADE=60°(旋转的意义),
所以△ADE是等边三角形
(有一个内角等于60°的等腰三角形是等边三角形),
所以AD=AE(等边三角形的三边相等),
∠DAE=60°(等边三角形的三内角等于60°). …………………(1分)
所以∠DAE-∠CAD=30°(等式性质),
即∠CAE=30°,
所以∠CAD=∠CAE(等量代换). ……………………………………(1分)
在△ACD与△ACE中,
?AC AC? (公共边),
??? ? ?CAD CAE(已证),
??AD AE? (已证),
所以△ACD≌△ACE(S.A.S). ………………………………………(1分)
所以∠ACD=∠ACE(全等三角形的对应边相等),
所以∠ACE=60°(等量代换),
所以∠ACD+∠ACE=120°(等式性质),
即∠DCE=120°,
所以∠B+∠DCE=180°(等式性质),
所以CE//AB(同旁内角互补,两直线平行). ………………………(1分)
解析:本题主要考查等边三角形与全等三角形有关概念,解题过程如上.
(3)解:因为AB=AC(已知),
所以∠ABC=∠ACB(等边对等角),
因为∠BAC=n(已知),
∠BAC+∠ABC+∠ACB=180°(三角形的内角和等于180°),
所以∠ABC+∠ACB=180°-n(等式性质),
1
所以∠ABC=∠ACB=90? ? n(等式性质).
2
因为AD⊥BC(已知),
所以BD=CD(等腰三角形底边上的中线与底边上的高互相重合),
1
∠BAD= ∠BAC(等腰三角形底边上的中线与顶角的平分线互相重合).
2
当∠BAC的度数为n,n有三种可能情况:n<90°,n>90°,n=90°.
(i) 当n<90°时:
延长AB、FD交于点G.
因为FC//AB(已知),
所以∠CBG=∠BCF(两直线平行,内错角相等),
第 13 页 共4页
∠ABC+∠BCF=180°(两直线平行,同旁内角互补),
1
所以∠BCF=90? ? n(等式性质),
2
1
所以∠CBG=90? ? n(等量代换).
2
在△BDG与△CDF中,
?? ? ?DBG DCF(已证),
??BD CD? (已证),
??? ? ?BDG CDF(对顶角相等),
所以△BDG≌△CDF(A.S.A),
所以DG=DF(全等三角形的对应边相等),
∠G=∠F(全等三角形的对应角相等).
因为AD=DF(旋转的意义),
所以DG=AD(等量代换),
所以∠BAD=∠G(等边对等角),
1
所以∠G= n(等量代换).
2
因为∠BAC=∠G+∠BDG
(三角形的一个外角等于与它不相邻的两个内角的和),
1 1
所以∠BDG=90? ? ?n n(等式性质),
2 2
所以∠BDG=90°-n(等式性质).
因为∠CDF=∠BDG(对顶角相等),
所以∠CDF=90°-n(等量代换),
所以直线DF与直线BC的夹角的度数是90°-n. …………(1分)
(ii)当n>90时:
延长FD交AB于点G.
因为FC//AB(已知),
所以∠CBG=∠BCF(两直线平行,内错角相等).
在△BDG与△CDF中,
?? ? ?DBG DCF(已证),
??BD CD? (已证),
??? ? ?BDG CDF(对顶角相等),
所以△BDG≌△CDF(A.S.A),
所以DG=DF(全等三角形的对应边相等),
∠B=∠DCF(全等三角形的对应角相等).
因为AD=DF(旋转的意义),
所以DG=AD(等量代换),
所以∠DAG=∠AGD(等边对等角),
1
所以∠AGD= n(等量代换).
2
因为∠AGD=∠B+∠BDG
(三角形的一个外角等于与它不相邻的两个内角的和),
1 1
所以∠BDG= n n? ? ?90 (等式性质),
2 2
所以∠BDG=n-90°(等式性质).
第 14 页 共4页
因为∠CDF=∠BDG(对顶角相等),
所以∠CDF=90°-n(等量代换),
所以直线DF与直线BC的夹角的度数是n-90°. …………(1分)
(iii)当n=90°时:
因为n=90°(已知),
所以∠ACD=45°,∠DAC=45°(等式性质),
所以∠ACD=∠DAC(等量代换),
所以AD=CD(等边对等角),
因为AD=DF(旋转的意义),
所以CD=DF(等量代换),
所以点C与点F重合,
即∠CDF=0°,
所以不符合题意,舍去. ………………………………………(1分)
所以直线DF与直线BC的夹角的度数是90°-n或n-90°. …………(1分)
解析:本题主要考查平行线、等腰三角形与全等三角形的有关概念,辅助线的添加、方程思想,以及
问题的多样性,解题过程中要注意考虑完整,正确添加辅助线,解题过程如上.
第 15 页 共4页
同课章节目录
