2.2 整式的加减 课件 2021-2022学年七年级数学人教版上册(第2课时 31张)
文档属性
| 名称 | 2.2 整式的加减 课件 2021-2022学年七年级数学人教版上册(第2课时 31张) |  | |
| 格式 | pptx | ||
| 文件大小 | 286.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 08:27:47 | ||
图片预览








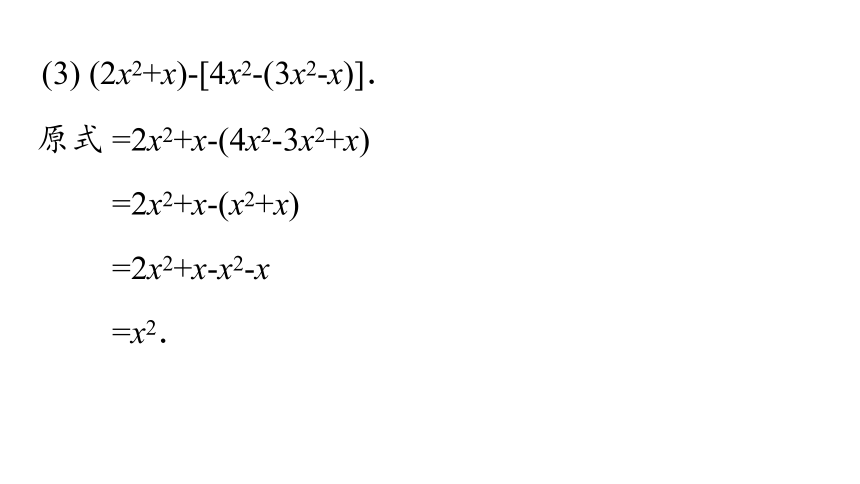



文档简介
2.2 整式的加减
人教版· 数学· 七年级(上)
第二章 整式的加减
第2课时 去括号
1.能运用运算律探究去括号法则。(重点)
2.会利用去括号法则将整式化简。(难点)
学习目标
请同学们观察下面的两个式子,你们知道该怎样化简吗?
100t+120(t-0.5)
100t-120(t-0.5)
导入新知
我们知道,化简带有括号的整式,应先去括号.上面两式去括号后分别为:
100t +120(t-0.5)= 100t +120t-60
100t -120(t-0.5)= 100t -120t+60
比较上面两个式子,你能发现去括号后符号变化的规律吗?
新知 去括号
合作探究
去括号法则:
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
注意:1.去括号时,要将括号连同它前面的符号一起去掉.
2.若括号前是“-”号,去括号时,括号内的各项都要变号,不能只改变括号内第一项或前几项的符号.
3.当括号前的因数不是±1时,要利用分配律将括号外的因数与括号内的每一项都相乘并去掉括号,不要漏乘括号内的任何一项.
比较 +(x-3) 与 -(x-3) 的区别.
+(x-3) 与 -(x-3) 可以分别看作 1 与 -1 分别乘 (x-3).
例 化简下列各式:
8a+2b+(5a-b); (2) (5a-3b)-3(a2-2b);
(3) (2x2+x)-[4x2-(3x2-x)].
解:(1) 原式=8a+2b+5a-b
=13a+b.
(2) 原式=(5a-3b)-(3a2-6b)
=5a-3b-3a2+6b
=-3a2+5a+3b.
利用分配律进行计算
原式 =2x2+x-(4x2-3x2+x)
=2x2+x-(x2+x)
=2x2+x-x2-x
=x2.
(3) (2x2+x)-[4x2-(3x2-x)].
去多重括号的方法
去多重括号时,一般由内向外,即先去小括号,再去中括号,最后去大括号;也可由外向内,即先去大括号,再去中括号,最后去小括号,且去大括号时,要将中括号看成一个整体,去中括号时,要将小括号看成一个整体.
例 两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1) 2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:顺水航速=船速+水速=(50+a)km/h,
逆水航速=船速 - 水速=(50-a)km/h.
解: (1) 2小时后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.
(2)2小时后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
例 两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1) 2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:(1) 2(0.5-2x)
=2×0.5-2×2x
=1-4x.
1.化简:
(1) 2(0.5-2x); (2) -4(1-12x).
?
(2) -4(1-12x).
=-4×1+(-4) ×(-12x)
=-4+2x.
?
课堂练习
2.长方形的周长为4a,一边长为(a-b) ,则另一边长为 .
a+b
2a-(a-b)=a+b.
去括号法则
括号外的因数是正数
符号相同
括号外的因数是负数
符号相反
去括号
去括号
归纳新知
1.将-2(a-b)去括号得到的结果是( )
A.-2a+b B.-2a-b
C.-2a+2b D.-2a-2b
2.-x+y-z的相反数是( )
A.-x-y+z B.x-y+z
C.x+y-z D.x+y+z
C
B
课后练习
3.下列等式中正确的是( )
A.2(a+1)=2a+1
B.-(a+b)=-a+b
C.-(a-b)=b-a
D.-(3-x)=3+x
4.下列各式中与a-b-c的值不相等的是( )
A.a-(b-c) B.a-(b+c)
C.(a-b)+(-c) D.(-c)-(b-a)
C
A
5.去掉下列各式中的括号:
(1)(x+y)-z=__________;
(2)x-(y+z)=____________;
(3)-1-2(x-y)= ________________;
(4)2(a-b)-3(x+y)= __________________.
x+y-z
x-y-z
-1-2x+2y
2a-2b-3x-3y
6.化简(a-b)-(a+b)的结果是( )
A.0 B.-2b C.2a D.2b
7.化简2(x-3)-3(2-3x)的结果为( )
A.11x-12 B.11x
C.-7x-12 D.-7x
B
A
a+1
0
10.化简:
(1)(x+2y)-(-2x+y);
解:原式=x+2y+2x-y=3x+y.
(2)(-b+3a)-2(a-b);
解:原式=-b+3a-2a+2b=a+b.
(3)3a2+2(a2-a)-4(a2-3a);
解:原式=3a2+2a2-2a-4a2+12a=a2+10a.
(4)2(-3a2+2a-1)-2(a2-3a-5).
解:原式=-6a2+4a-2-2a2+6a+10=-8a2+10a+8.
11.已知三个连续奇数,最小的一个奇数是2n+1(n为自然数),
则这三个连续奇数的和为( )
A.6n+6 B.2n+9
C.6n+9 D.6n+3
12.已知长方形的一边长为3m+2n,另一边比它短m-n,
则这个长方形的周长是( )
A.10m+10n B.5m+5n
C.2m+3n D.6n+3
C
A
13.轮船在静水中的航速为a km/h,水流速度为b km/h,
轮船顺水航行5 h的路程是 ___________km,
轮船逆水航行5 h的路程是 __________km,
该轮船顺水航行的路程比逆水航行的路程多____ km.
(5a+5b)
(5a-5b)
10b
D
C
16.当1≤m<3时,化简|m-1|-|m-3|=________.
17.已知a-2b=1,则3-2a+4b=___.
18.甲、乙、丙三人一起按如下步骤玩纸牌游戏:
第一步:每个人都发给x张牌(其中x≥2);
第二步:甲拿出两张牌给乙;
第三步:丙拿出一张牌给乙;
第四步:此时甲有几张牌,乙就拿几张牌给甲.
这时,甲准确地说出乙现有的牌的张数,你认为乙此时有___张牌.
2m-4
1
5
19.先化简,再求值:
(1)-3(3x2-2x+1)-3(-2x2-5x),其中x=-1;
解:原式=-9x2+6x-3+6x2+15x=-3x2+21x-3,
当x=-1时,原式=-3×(-1)2+21×(-1)-3=-3-21-3=-27.
(2)a-2[3a+b-2(a+b)],其中a=-20,b=10.
解:原式=a-2(3a+b-2a-2b)=a-2(a-b)=a-2a+2b=-a+2b.
当a=-20,b=10时,原式=-(-20)+2×10=40.
20.有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+
(-x3+3x2y-y3)的值,其中x=2,y=-1.甲同学把x=2误抄成x=-2,
但他计算的结果也是正确的,试说明理由,并求出这个结果.
解:原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3=-2y3.
因为化简的结果中不含x,所以原式的值与x的值无关,
所以甲同学计算的结果也是正确的.当y=-1时,原式=-2×(-1)3=2.
21.学校将组织学生参加元旦长跑活动.七年级二班班主任王老师对全班46名同学说:想参加的同学举手,如果举手的人数和没有举手的人数之差是奇数,我只派9个班干部参加;如果是偶数,让全班同学都参加.请用学过的整式的知识来说明老师的真实想法.
解:设举手的人数为x,那么没有举手的人数为(46-x),举手的人数和没有举手的人数之差为x-(46-x)=x-46+x=2x-46=2(x-23),因为x是整数,所以x-23是整数,所以2(x-23)是偶数,即无论有多少名学生举手,最后的结果一定是偶数,所以老师的真实想法是让全班同学都参加.
再
见
人教版· 数学· 七年级(上)
第二章 整式的加减
第2课时 去括号
1.能运用运算律探究去括号法则。(重点)
2.会利用去括号法则将整式化简。(难点)
学习目标
请同学们观察下面的两个式子,你们知道该怎样化简吗?
100t+120(t-0.5)
100t-120(t-0.5)
导入新知
我们知道,化简带有括号的整式,应先去括号.上面两式去括号后分别为:
100t +120(t-0.5)= 100t +120t-60
100t -120(t-0.5)= 100t -120t+60
比较上面两个式子,你能发现去括号后符号变化的规律吗?
新知 去括号
合作探究
去括号法则:
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
注意:1.去括号时,要将括号连同它前面的符号一起去掉.
2.若括号前是“-”号,去括号时,括号内的各项都要变号,不能只改变括号内第一项或前几项的符号.
3.当括号前的因数不是±1时,要利用分配律将括号外的因数与括号内的每一项都相乘并去掉括号,不要漏乘括号内的任何一项.
比较 +(x-3) 与 -(x-3) 的区别.
+(x-3) 与 -(x-3) 可以分别看作 1 与 -1 分别乘 (x-3).
例 化简下列各式:
8a+2b+(5a-b); (2) (5a-3b)-3(a2-2b);
(3) (2x2+x)-[4x2-(3x2-x)].
解:(1) 原式=8a+2b+5a-b
=13a+b.
(2) 原式=(5a-3b)-(3a2-6b)
=5a-3b-3a2+6b
=-3a2+5a+3b.
利用分配律进行计算
原式 =2x2+x-(4x2-3x2+x)
=2x2+x-(x2+x)
=2x2+x-x2-x
=x2.
(3) (2x2+x)-[4x2-(3x2-x)].
去多重括号的方法
去多重括号时,一般由内向外,即先去小括号,再去中括号,最后去大括号;也可由外向内,即先去大括号,再去中括号,最后去小括号,且去大括号时,要将中括号看成一个整体,去中括号时,要将小括号看成一个整体.
例 两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1) 2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:顺水航速=船速+水速=(50+a)km/h,
逆水航速=船速 - 水速=(50-a)km/h.
解: (1) 2小时后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.
(2)2小时后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
例 两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1) 2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:(1) 2(0.5-2x)
=2×0.5-2×2x
=1-4x.
1.化简:
(1) 2(0.5-2x); (2) -4(1-12x).
?
(2) -4(1-12x).
=-4×1+(-4) ×(-12x)
=-4+2x.
?
课堂练习
2.长方形的周长为4a,一边长为(a-b) ,则另一边长为 .
a+b
2a-(a-b)=a+b.
去括号法则
括号外的因数是正数
符号相同
括号外的因数是负数
符号相反
去括号
去括号
归纳新知
1.将-2(a-b)去括号得到的结果是( )
A.-2a+b B.-2a-b
C.-2a+2b D.-2a-2b
2.-x+y-z的相反数是( )
A.-x-y+z B.x-y+z
C.x+y-z D.x+y+z
C
B
课后练习
3.下列等式中正确的是( )
A.2(a+1)=2a+1
B.-(a+b)=-a+b
C.-(a-b)=b-a
D.-(3-x)=3+x
4.下列各式中与a-b-c的值不相等的是( )
A.a-(b-c) B.a-(b+c)
C.(a-b)+(-c) D.(-c)-(b-a)
C
A
5.去掉下列各式中的括号:
(1)(x+y)-z=__________;
(2)x-(y+z)=____________;
(3)-1-2(x-y)= ________________;
(4)2(a-b)-3(x+y)= __________________.
x+y-z
x-y-z
-1-2x+2y
2a-2b-3x-3y
6.化简(a-b)-(a+b)的结果是( )
A.0 B.-2b C.2a D.2b
7.化简2(x-3)-3(2-3x)的结果为( )
A.11x-12 B.11x
C.-7x-12 D.-7x
B
A
a+1
0
10.化简:
(1)(x+2y)-(-2x+y);
解:原式=x+2y+2x-y=3x+y.
(2)(-b+3a)-2(a-b);
解:原式=-b+3a-2a+2b=a+b.
(3)3a2+2(a2-a)-4(a2-3a);
解:原式=3a2+2a2-2a-4a2+12a=a2+10a.
(4)2(-3a2+2a-1)-2(a2-3a-5).
解:原式=-6a2+4a-2-2a2+6a+10=-8a2+10a+8.
11.已知三个连续奇数,最小的一个奇数是2n+1(n为自然数),
则这三个连续奇数的和为( )
A.6n+6 B.2n+9
C.6n+9 D.6n+3
12.已知长方形的一边长为3m+2n,另一边比它短m-n,
则这个长方形的周长是( )
A.10m+10n B.5m+5n
C.2m+3n D.6n+3
C
A
13.轮船在静水中的航速为a km/h,水流速度为b km/h,
轮船顺水航行5 h的路程是 ___________km,
轮船逆水航行5 h的路程是 __________km,
该轮船顺水航行的路程比逆水航行的路程多____ km.
(5a+5b)
(5a-5b)
10b
D
C
16.当1≤m<3时,化简|m-1|-|m-3|=________.
17.已知a-2b=1,则3-2a+4b=___.
18.甲、乙、丙三人一起按如下步骤玩纸牌游戏:
第一步:每个人都发给x张牌(其中x≥2);
第二步:甲拿出两张牌给乙;
第三步:丙拿出一张牌给乙;
第四步:此时甲有几张牌,乙就拿几张牌给甲.
这时,甲准确地说出乙现有的牌的张数,你认为乙此时有___张牌.
2m-4
1
5
19.先化简,再求值:
(1)-3(3x2-2x+1)-3(-2x2-5x),其中x=-1;
解:原式=-9x2+6x-3+6x2+15x=-3x2+21x-3,
当x=-1时,原式=-3×(-1)2+21×(-1)-3=-3-21-3=-27.
(2)a-2[3a+b-2(a+b)],其中a=-20,b=10.
解:原式=a-2(3a+b-2a-2b)=a-2(a-b)=a-2a+2b=-a+2b.
当a=-20,b=10时,原式=-(-20)+2×10=40.
20.有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+
(-x3+3x2y-y3)的值,其中x=2,y=-1.甲同学把x=2误抄成x=-2,
但他计算的结果也是正确的,试说明理由,并求出这个结果.
解:原式=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3=-2y3.
因为化简的结果中不含x,所以原式的值与x的值无关,
所以甲同学计算的结果也是正确的.当y=-1时,原式=-2×(-1)3=2.
21.学校将组织学生参加元旦长跑活动.七年级二班班主任王老师对全班46名同学说:想参加的同学举手,如果举手的人数和没有举手的人数之差是奇数,我只派9个班干部参加;如果是偶数,让全班同学都参加.请用学过的整式的知识来说明老师的真实想法.
解:设举手的人数为x,那么没有举手的人数为(46-x),举手的人数和没有举手的人数之差为x-(46-x)=x-46+x=2x-46=2(x-23),因为x是整数,所以x-23是整数,所以2(x-23)是偶数,即无论有多少名学生举手,最后的结果一定是偶数,所以老师的真实想法是让全班同学都参加.
再
见
同课章节目录
