平面直角坐标系中的图形
图片预览




文档简介
(共28张PPT)
直角坐标系
中的图形
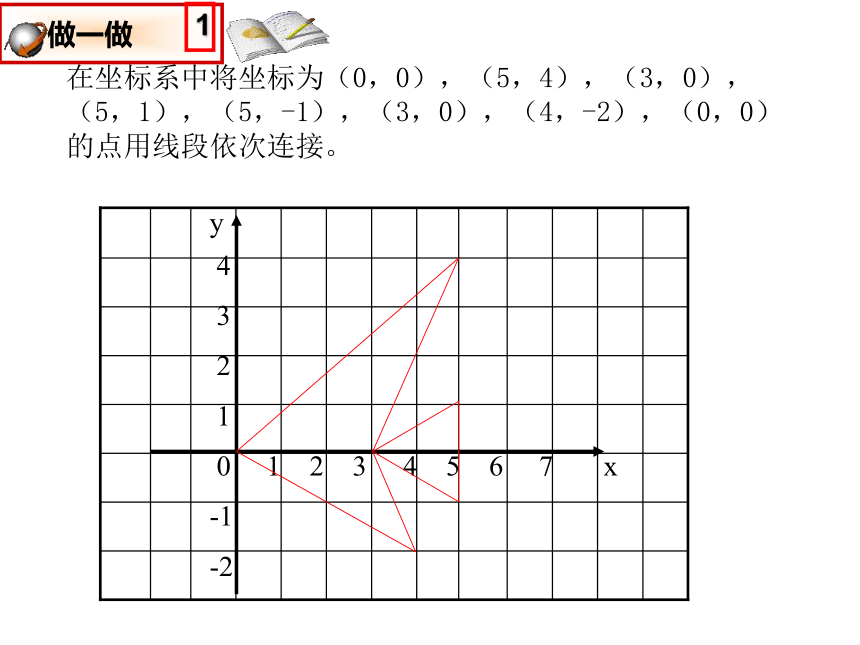
在坐标系中将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)的点用线段依次连接。
做一做
1
y
-2
1
2
3
4
1
2
3
4
5
6
7
0
-1
x
例题
2
例1 将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
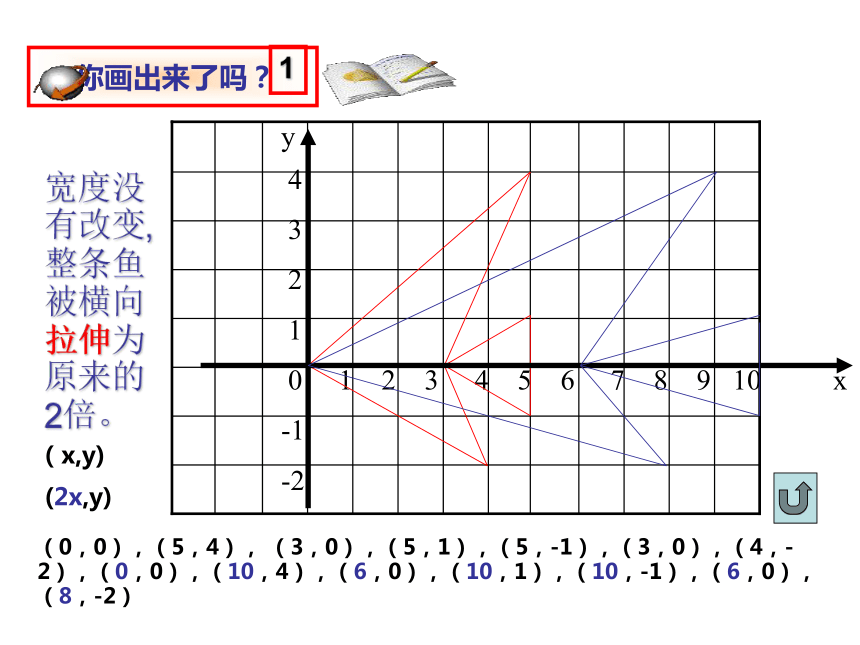
(1)纵坐标保持不变,横坐标分别变成原来的2倍,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
你画出来了吗?
1
y
-2
1
2
3
4
1
2
3
4
5
6
7
0
-1
x
8
9
10
(0,0),(5,4), (3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),(10,4),(6,0),(10,1),(10,-1),(6,0),(8,-2)
宽度没有改变,整条鱼被横向拉伸为原来的 2倍。
(x,y)
(2x,y)
例题
2
如果将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
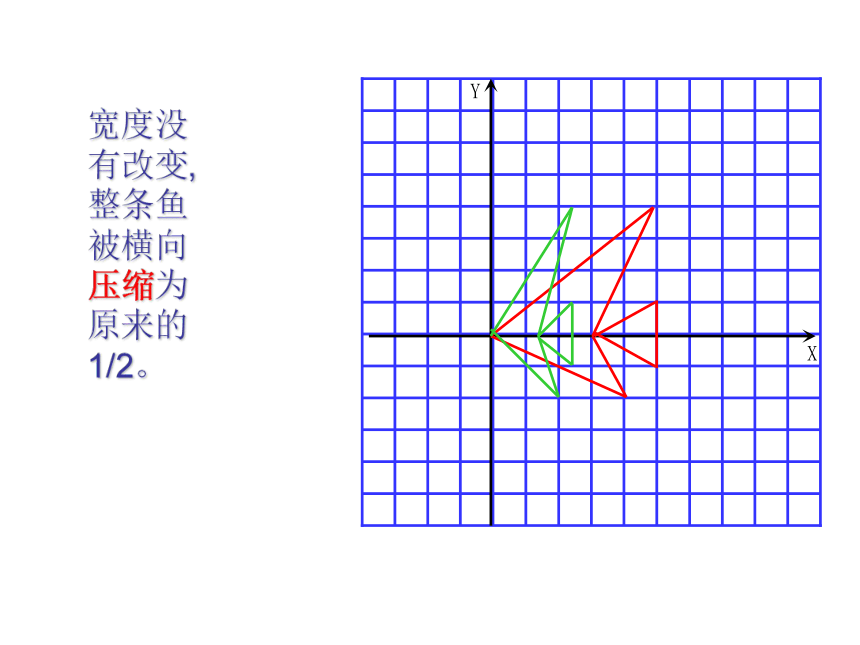
(2)纵坐标保持不变,横坐标分别变成原来的1/2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
宽度没有改变,整条鱼被横向压缩为原来的1/2。
想一想
2
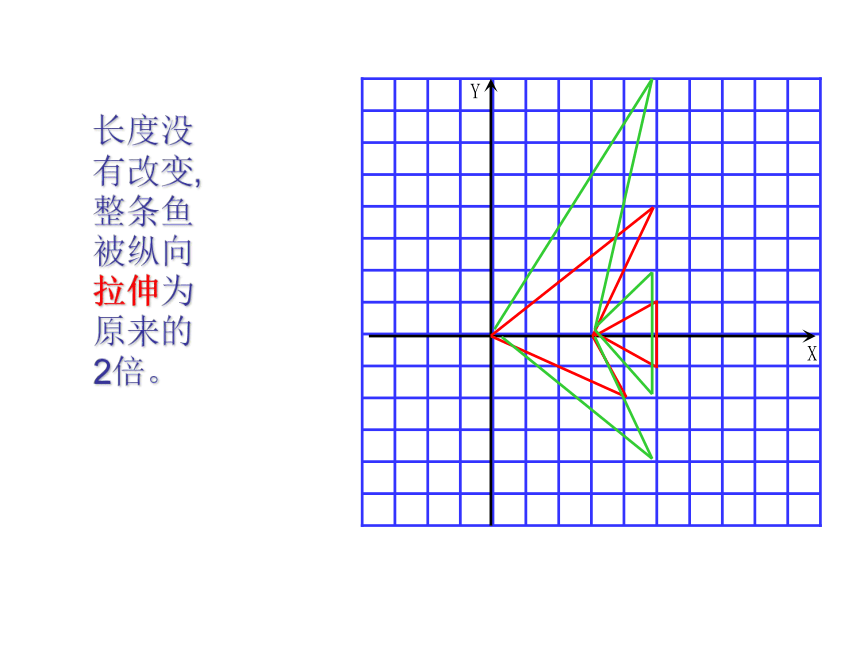
1. 横坐标保持不变,纵坐标分别变成原来的2倍,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化
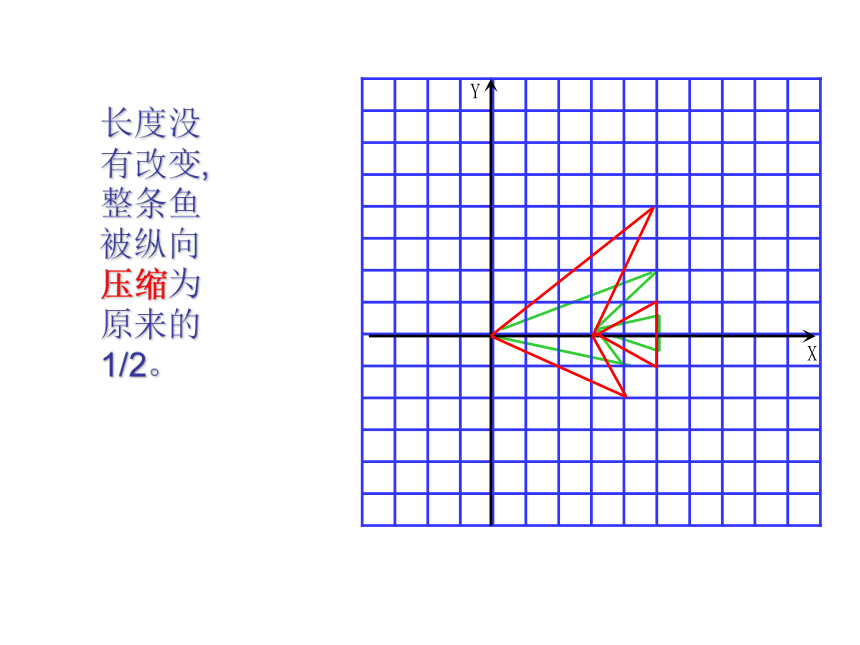
2. 横坐标保持不变,纵坐标分别变成原来的1/2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
长度没有改变,整条鱼被纵向拉伸为原来的 2倍。
X
Y
长度没有改变,整条鱼被纵向压缩为原来的1/2。
图案是如何拉伸或压缩的
☆纵坐标保持不变,横坐标分别变成原来的a倍( a为正整数 )或 ,则图案沿水平方向(横向)拉伸或压缩为原来的的a倍或 ;
☆横坐标保持不变,纵坐标分别变成原来的a倍 ( a为正整数 )或 ,则图案沿竖直方向(纵向)拉伸或压缩为原来的的a倍或 。
例题
2
例1 将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
(3)纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
y
-2
1
2
3
4
1
2
3
4
5
6
7
0
-1
x
8
9
10
(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(3,0),(8,4),(6,0),(8,1),(8,-1),(6,0),(7,-2)。
(x,y)
(x+3,y)
鱼的形状、大小不变,整条鱼向右平移了3个单位长度。
你画出来了吗?
2
例题
2
如果将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
(4)纵坐标保持不变,横坐标分别减2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
鱼的形状、大小不变,整条鱼向左平移了2个单位长度
1. 横坐标保持不变,纵坐标分别加3,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
2. 横坐标保持不变,纵坐标分别减2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
鱼的形状、大小不变,整条鱼向上平移了3个单位长度
X
Y
鱼的形状、大小不变,整条鱼向下平移了2个单位长度
图案是如何平移的
☆纵坐标保持不变,横坐标分别加或减a( a>0),则图案沿水平方向向右或向左平移;
☆横坐标保持不变,纵坐标分别加或减a( a>0),则图案沿竖直方向向上或向下平移;
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
②
如上图:
与①中的三角形相比,②中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
③
如上图:
与①中的三角形相比,③中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
④
如上图:
与①中的三角形相比,④中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
⑤
如上图:
与①中的三角形相比,⑤中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
⑥
如上图:
如何由①中的三角形变换为⑥中的三角形
今天你有什么收获
1、图案拉长(或压缩) :
☆纵坐标保持不变,横坐标分别变成原来的a( a为正整数 )或 倍,则图案沿水平方向拉长(或压缩)为原来的的a倍或 倍;
☆横坐标保持不变,纵坐标分别变成原来的a ( a为正整数 )或 倍,则图案沿竖直方向拉长(或压缩)为原来的的a倍或 倍。
今天你有什么收获
2、 图案平移:
☆纵坐标保持不变,横坐标分别加或减a( a>0),则图案沿水平方向向右或向左平移;
☆横坐标保持不变,纵坐标分别加或减a( a>0),则图案沿竖直方向向上或向下平移;
今天你有什么收获
横向:纵坐标不变,横坐标乘a或
在平面直角坐标系中,坐标的变化引起图形的变化;图形的变化也会引起坐标的变化。
平移
伸缩
横向:纵坐标不变,横坐标加减a
纵向:横坐标不变,纵坐标加减a
纵向:横坐标不变,纵坐标乘a或
( a>0)
最后考考你的想象能力
请你设计一个方案:将下图坐标系中的第一象限内的M变换成第三象限内的M。
X
Y
1:伴你学
2:预习 P92-93 在坐标纸上画出图5-20
布 置 作 业
直角坐标系
中的图形
在坐标系中将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)的点用线段依次连接。
做一做
1
y
-2
1
2
3
4
1
2
3
4
5
6
7
0
-1
x
例题
2
例1 将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
(1)纵坐标保持不变,横坐标分别变成原来的2倍,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
你画出来了吗?
1
y
-2
1
2
3
4
1
2
3
4
5
6
7
0
-1
x
8
9
10
(0,0),(5,4), (3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),(10,4),(6,0),(10,1),(10,-1),(6,0),(8,-2)
宽度没有改变,整条鱼被横向拉伸为原来的 2倍。
(x,y)
(2x,y)
例题
2
如果将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
(2)纵坐标保持不变,横坐标分别变成原来的1/2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
宽度没有改变,整条鱼被横向压缩为原来的1/2。
想一想
2
1. 横坐标保持不变,纵坐标分别变成原来的2倍,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化
2. 横坐标保持不变,纵坐标分别变成原来的1/2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
长度没有改变,整条鱼被纵向拉伸为原来的 2倍。
X
Y
长度没有改变,整条鱼被纵向压缩为原来的1/2。
图案是如何拉伸或压缩的
☆纵坐标保持不变,横坐标分别变成原来的a倍( a为正整数 )或 ,则图案沿水平方向(横向)拉伸或压缩为原来的的a倍或 ;
☆横坐标保持不变,纵坐标分别变成原来的a倍 ( a为正整数 )或 ,则图案沿竖直方向(纵向)拉伸或压缩为原来的的a倍或 。
例题
2
例1 将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
(3)纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
y
-2
1
2
3
4
1
2
3
4
5
6
7
0
-1
x
8
9
10
(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(3,0),(8,4),(6,0),(8,1),(8,-1),(6,0),(7,-2)。
(x,y)
(x+3,y)
鱼的形状、大小不变,整条鱼向右平移了3个单位长度。
你画出来了吗?
2
例题
2
如果将上图中的 点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做如下的变化:
(4)纵坐标保持不变,横坐标分别减2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
鱼的形状、大小不变,整条鱼向左平移了2个单位长度
1. 横坐标保持不变,纵坐标分别加3,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
2. 横坐标保持不变,纵坐标分别减2,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
X
Y
鱼的形状、大小不变,整条鱼向上平移了3个单位长度
X
Y
鱼的形状、大小不变,整条鱼向下平移了2个单位长度
图案是如何平移的
☆纵坐标保持不变,横坐标分别加或减a( a>0),则图案沿水平方向向右或向左平移;
☆横坐标保持不变,纵坐标分别加或减a( a>0),则图案沿竖直方向向上或向下平移;
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
②
如上图:
与①中的三角形相比,②中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
③
如上图:
与①中的三角形相比,③中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
④
如上图:
与①中的三角形相比,④中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
⑤
如上图:
与①中的三角形相比,⑤中的三角形发生哪些变化?直角三角形的顶点坐标发生了哪些变化?
考考你的反应能力
0
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
0
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
X
Y
①
⑥
如上图:
如何由①中的三角形变换为⑥中的三角形
今天你有什么收获
1、图案拉长(或压缩) :
☆纵坐标保持不变,横坐标分别变成原来的a( a为正整数 )或 倍,则图案沿水平方向拉长(或压缩)为原来的的a倍或 倍;
☆横坐标保持不变,纵坐标分别变成原来的a ( a为正整数 )或 倍,则图案沿竖直方向拉长(或压缩)为原来的的a倍或 倍。
今天你有什么收获
2、 图案平移:
☆纵坐标保持不变,横坐标分别加或减a( a>0),则图案沿水平方向向右或向左平移;
☆横坐标保持不变,纵坐标分别加或减a( a>0),则图案沿竖直方向向上或向下平移;
今天你有什么收获
横向:纵坐标不变,横坐标乘a或
在平面直角坐标系中,坐标的变化引起图形的变化;图形的变化也会引起坐标的变化。
平移
伸缩
横向:纵坐标不变,横坐标加减a
纵向:横坐标不变,纵坐标加减a
纵向:横坐标不变,纵坐标乘a或
( a>0)
最后考考你的想象能力
请你设计一个方案:将下图坐标系中的第一象限内的M变换成第三象限内的M。
X
Y
1:伴你学
2:预习 P92-93 在坐标纸上画出图5-20
布 置 作 业
