2020-2021学年上海市静安区七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市静安区七年级(下)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 703.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 05:30:13 | ||
图片预览



文档简介
2020-2021学年上海市静安区七年级(下)期末数学试卷
一、填空题(每题2分,满分30分).
1.0.01的平方根是 .
2.已知a3=216,那么a= .
3.已知实数a≤0≤b,化简:= .
4.计算:4= .
5.月球沿着一定的轨道围绕地球运动,它的半长轴约为385000千米,这个数据用科学记数法精确到万位表示,应记为 千米.
6.对于近似数0.0680,它有 个有效数字.
7.在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 .
8.在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= .
9.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 度.
10.如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是 .
11.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 度.
12.已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 cm.
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
14.已知△ABC中,AB=AC,∠B=50°,如果D是边BC的中点,那么∠CAD= 度.
15.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 .
二、选择题:(本大题共5题,每小题2分,满分10分)
16.如图,数轴上点P表示的数可能是( )
A.﹣ B. C.﹣3.7 D.﹣
17.下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
18.若∠A,∠B互为补角,且∠A<∠B,则∠A的余角是( )
A.(∠A+∠B) B.∠B C.(∠B﹣∠A) D.∠A
19.在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
20.早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
三、简答题:(本大题共6题,每小题5分,满分30分)
21.计算:(2﹣)0+()﹣1﹣.
22.计算:(﹣+3)×﹣÷.
23.用幂的性质计算:(5﹣17)?(5+17).
24.计算:×÷.
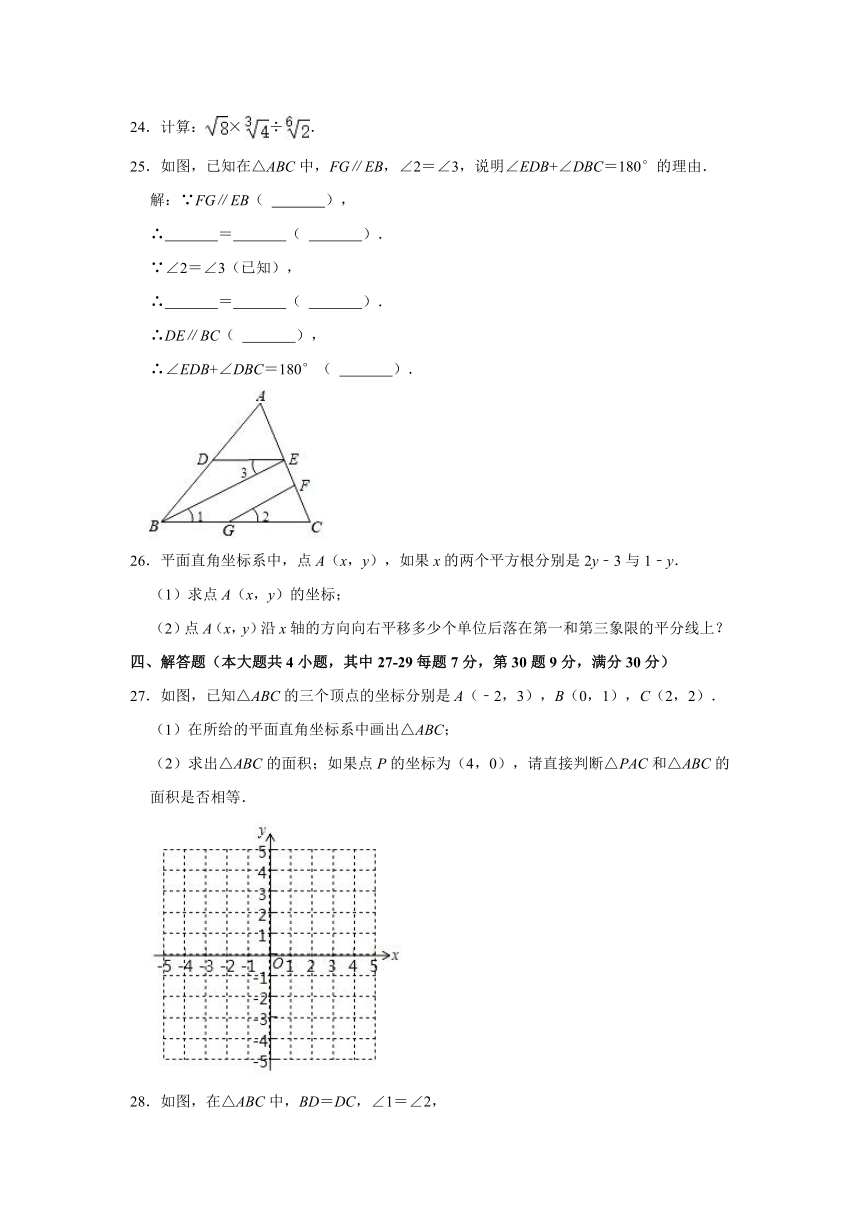
25.如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( ),
∴ = ( ).
∵∠2=∠3(已知),
∴ = ( ).
∴DE∥BC( ),
∴∠EDB+∠DBC=180°( ).
26.平面直角坐标系中,点A(x,y),如果x的两个平方根分别是2y﹣3与1﹣y.
(1)求点A(x,y)的坐标;
(2)点A(x,y)沿x轴的方向向右平移多少个单位后落在第一和第三象限的平分线上?
四、解答题(本大题共4小题,其中27-29每题7分,第30题9分,满分30分)
27.如图,已知△ABC的三个顶点的坐标分别是A(﹣2,3),B(0,1),C(2,2).
(1)在所给的平面直角坐标系中画出△ABC;
(2)求出△ABC的面积;如果点P的坐标为(4,0),请直接判断△PAC和△ABC的面积是否相等.
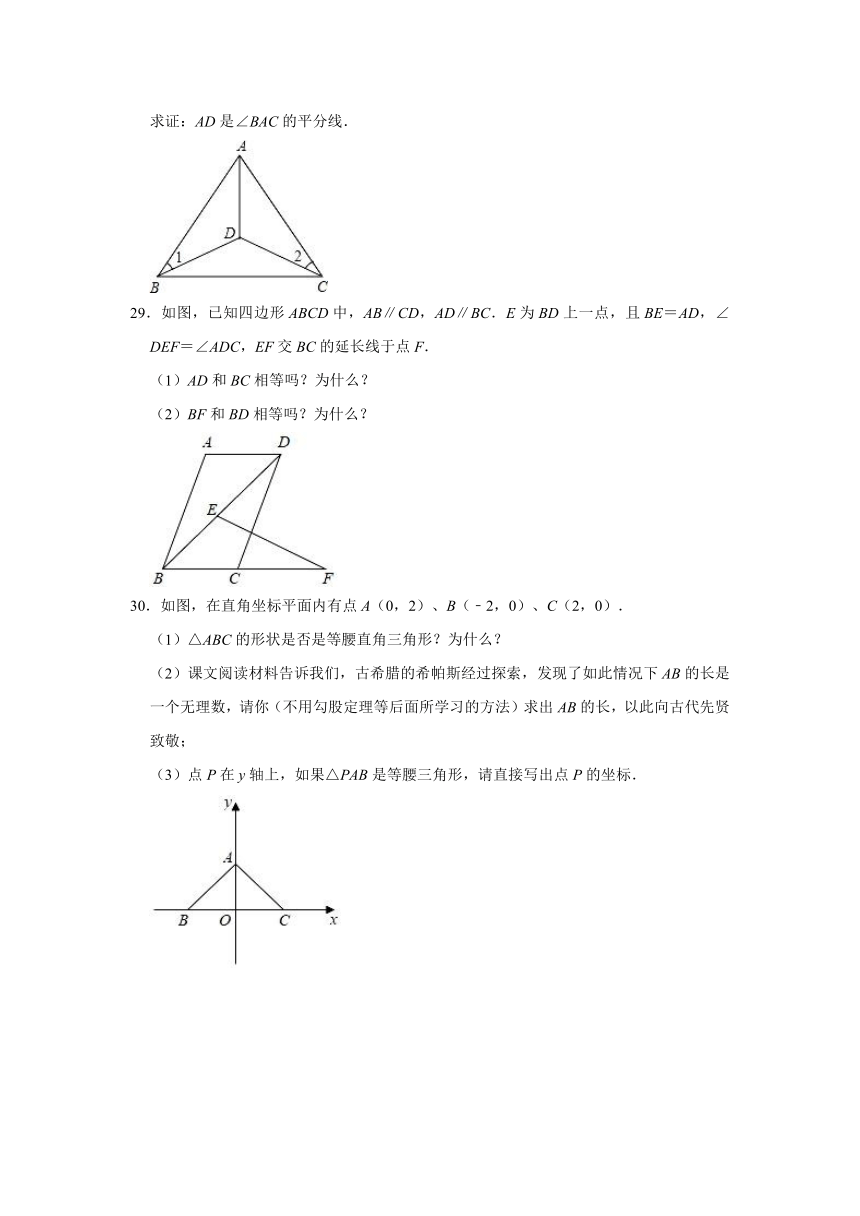
28.如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
29.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
30.如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
参考答案
一、填空题(每题2分,满分30分)
1.0.01的平方根是 ±0.1 .
【分析】根据平方根的定义即可求出答案.
解:0.01的平方根是±0.1,
故答案为:±0.1;
2.已知a3=216,那么a= 6 .
【分析】根据立方根的定义解答即可.
解:因为a3=216,
所以a==6.
故答案为:6.
3.已知实数a≤0≤b,化简:= b﹣a .
【分析】直接利用a,b的符号得出a﹣b<0,再利用二次根式的性质化简即可.
解:∵a≤0≤b,
∴a﹣b<0,
∴=|a﹣b|=b﹣a.
故答案为:b﹣a.
4.计算:4= .
【分析】幂的n次方公式:(am)n=amn,
解:因为4=22,所以
5.月球沿着一定的轨道围绕地球运动,它的半长轴约为385000千米,这个数据用科学记数法精确到万位表示,应记为 3.9×105 千米.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
解:将385000千米用科学记数法精确到万位表示,应记为3.9×105.
故答案是:3.9×105.
6.对于近似数0.0680,它有 3 个有效数字.
【分析】一个近似数的有效数字是从左边第一个不是0的数字起,后面所有的数字都是这个数的有效数字.
解:近似数0.0680的有效数字是6,8,0,共有3个.
故答案是:3.
7.在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 y=4 .
【分析】垂直于y轴的直线,纵坐标相等为4,所以为直线:y=4.
解:由题意得:经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线为:y=4,
故答案为:y=4.
8.在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= 2 .
【分析】直接利用x轴上点的坐标特点得出2﹣a=0,进而求出a的值.
解:∵点Q(a+1,2﹣a)在x轴上,
∴2﹣a=0,
解得:a=2.
故答案为:2.
9.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 25 度.
【分析】根据对顶角相等和角平分线的定义可得答案.
解:∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD,
又∵∠ACO=∠BOD,
∴∠BOE=∠AOC=×50°=25°,
故答案为:25.
10.如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是 同位角相等,两直线平行 .
【分析】根据同位角相等两直线平行判断即可.
解:如图,
∵∠BEF=∠DFG,
∴AB∥CD(同位角相等两直线平行),
故答案为:同位角相等两直线平行.
11.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 46 度.
【分析】根据平行线的性质及可得到答案.
解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=126°,∠2=80°,
∴∠3=∠1﹣∠2=46°,
故答案为:46.
12.已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 17 cm.
【分析】根据题意分两种情况:第一种是底边长为7时构不成三角形要排除,第二种情况是底边长为3,然后再将三边长相加即可求得答案.
解:∵等腰三角形的两条边长分别是3cm、7cm,
∴当此三角形的腰长为3cm时,3+3<7,不能构成三角形,故排除,
∴此三角形的腰长为7cm,底边长为3cm,
∴此等腰三角形的周长=7+7+3=17cm,
故答案为:17.
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 90 度.
【分析】连接BD,根据三角形内角和定理求出∠CBD+∠CDB,根据平行线的性质求出∠ABD+∠EDB,即可求出答案.
解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)
=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)
=360°﹣(90°+180°)
=90°,
故答案为:90.
14.已知△ABC中,AB=AC,∠B=50°,如果D是边BC的中点,那么∠CAD= 40 度.
【分析】首先利用等腰三角形的底角的度数求得另一个底角的度数,然后根据等腰三角形“三线合一”的性质求得答案即可.
解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∵D是边BC的中点,
∴AD⊥BC,
∴∠CAD=40°,
故答案为:40.
15.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 ﹣1或0 .
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.
解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
二、选择题:(本大题共5题,每小题2分,满分10分)
16.如图,数轴上点P表示的数可能是( )
A.﹣ B. C.﹣3.7 D.﹣
【分析】根据数轴上点的位置及无理数的估算进行判断.
解:设点P表示的数为a,
由题意可得:﹣3<a<﹣2,
∵﹣3.7<﹣3<﹣<﹣2<﹣<,
∴选项A符合题意,
故选:A.
17.下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
【分析】根据选项中的说法可以判断两个三角形是否全等,从而可以解答本题.
解:周长相等的锐角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项A错误;
周长相等的直角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项B错误;
周长相等的钝角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项C错误;
周长相等的等边三角形一定全等,因为周长相等,三条边一定对应相等,利用SSS,可以说明两个三角形全等,故选项D正确;
故选:D.
18.若∠A,∠B互为补角,且∠A<∠B,则∠A的余角是( )
A.(∠A+∠B) B.∠B C.(∠B﹣∠A) D.∠A
【分析】根据互为补角的和得到∠A,∠B的关系式,再根据互为余角的和等于90°表示出∠A的余角,然后把常数消掉整理即可得解.
解:根据题意得,∠A+∠B=180°,
∴∠A的余角为:90°﹣∠A=﹣∠A,
=(∠A+∠B)﹣∠A,
=(∠B﹣∠A).
故选:C.
19.在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
【分析】根据第四象限点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
解:∵点B在第四象限,且到x轴的距离为2,到y轴的距离为5,
∴点B的横坐标为5,纵坐标为﹣2,
∴点B的坐标为(5,﹣2).
故选:A.
20.早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
【分析】根据分针旋转的速度乘分针旋转的时间,可得分针的旋转角,根据秒针旋转的速度成秒针旋转的时间,可得秒针的旋转角,根据分针的旋转角减去秒针的旋转角,可得答案.
解:设t分后时钟的分针和时针第一次垂直,依题意有
6t﹣0.5t=360﹣120﹣90,
解得t=27.
故早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是8点27分.
故选:C.
三、简答题:(本大题共6题,每小题5分,满分30分)
21.计算:(2﹣)0+()﹣1﹣.
【分析】根据零指数幂的意义,二次根式的加减运算以及乘除运算即可求出答案.
解:原式=1+﹣|2﹣|
=1+﹣(2﹣)
=1+﹣2+
=2﹣1.
22.计算:(﹣+3)×﹣÷.
【分析】根据二次根式的加减运算以及乘除运算即可求出答案.
解:原式=﹣2+3×2﹣
=﹣2+6﹣2
=2.
23.用幂的性质计算:(5﹣17)?(5+17).
【分析】平方差公式:(a+b)(a﹣b)=a2﹣b2,题中数据与公式对应:a=5,b=,a2=52=25,b2=()2=17×=171=17
解:原式=[(5﹣)(5+)]
=(25﹣17)
=8
=
=2
24.计算:×÷.
【分析】直接利用分数指数幂的性质将原式变形计算得出答案.
解:原式=2×2÷2
=2
=22
=4.
25.如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( 已知 ),
∴ ∠1 = ∠2 ( 两直线平行,同位角相等 ).
∵∠2=∠3(已知),
∴ ∠1 = ∠3 ( 等量代换 ).
∴DE∥BC( 内错角相等,两直线平行 ),
∴∠EDB+∠DBC=180°( 两直线平行,同旁内角互补 ).
【分析】利用平行线的性质和判定解答即可
解:∵FG∥EB(已知),
∴∠1=∠2(两直线平行,同位角相等).
∵∠2=∠3(已知),
∴∠1=∠3(等量代换).
∴DE∥BC(内错角相等,两直线平行).
∴∠EDB+∠DBC=180°(两直线平行,同旁内角互补).
故答案为:已知;∠1;∠2;两直线平行,同位角相等;∠1;∠3;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补.
26.平面直角坐标系中,点A(x,y),如果x的两个平方根分别是2y﹣3与1﹣y.
(1)求点A(x,y)的坐标;
(2)点A(x,y)沿x轴的方向向右平移多少个单位后落在第一和第三象限的平分线上?
【分析】(1)根据平方根的概念得出y的方程,进而解答即可;
(2)根据平移的性质解答即可.
解:(1)根据题意得:(2y﹣3)+(1﹣y)=0,
解得:y=2,
可得:x=(2y﹣3)2=1,
所求的点A的坐标为A(1,2);
(2)根据题意得:(1,2)→(2,2),
点A(1,2)沿x轴的方向向右平移1个单位后落在第一和第三象限的平分线上.
四、解答题(本大题共4小题,其中27-29每题7分,第30题9分,满分30分)
27.如图,已知△ABC的三个顶点的坐标分别是A(﹣2,3),B(0,1),C(2,2).
(1)在所给的平面直角坐标系中画出△ABC;
(2)求出△ABC的面积;如果点P的坐标为(4,0),请直接判断△PAC和△ABC的面积是否相等.
【分析】(1)根据A,B,C的坐标作出A,B,C三点即可.
(2)利用分割法把三角形面积转化为矩形面积减去三个三角形面积即可,再利用等高模型解决问题.
解:(1)如图,△ABC即为所求.
(2)连接PB.
S△ABC=2×4﹣×2×2﹣×1×4﹣×1×2=3.
∵PB∥AC,
∴S△PAC=S△ABC.
28.如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
【分析】根据BD=DC得出∠DBC=∠DCB,进而利用全等三角形的判定和性质证明即可.
【解答】证明:∵BD=DC,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
29.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
【分析】(1)根据平行线的性质和全等三角形的判定和性质得出△ABD与△CDB全等,进而利用全等三角形的性质解答即可;
(2)根据平行线的性质和全等三角形的判定和性质得出△EFB与△CDB全等,进而解答即可.
解:(1)AD=CB,
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,
∵AD=CB,BE=AD,
∴BC=BE,
∵AD∥BC,
∴∠ADB=∠DBF,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
30.如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
【分析】(1)由等腰三角形的性质可求∠ABO=∠BAO=45°,∠ACO=∠CAO=45°,可得结论;
(2)由面积法可求AB的长;
(3)分三种情况讨论,由等腰三角形的性质可求解.
解:(1)△ABC是等腰直角三角形,
理由如下:∵点A(0,2)、B(﹣2,0)、C(2,0),
∴OA=OB=OC=2,
又∵∠AOB=∠AOC=90°,
∴∠ABO=∠BAO=45°,∠ACO=∠CAO=45°,
∴∠BAC=90°,∠ABO=∠ACO,
∴AB=AC,
∴△ABC是等腰直角三角形;
(2)∵S△ABC=×AB×AC=×BC×AO,
∴AB2=4×2=8,
∴AB=2,AB=﹣2(舍去),
∴AB的长为2;
(3)若PB=PA,则点P与点O重合,即点P坐标为(0,0);
若BA=BP=2,且OA⊥OB,
∴OA=OP=2,
∴点P(0,﹣2),
若AB=AP=2,且点A(0,2),
∴点P(0,2+2)或(0,2﹣2),
综上所述:点P的坐标为(0,0)或(0,﹣2)或(0,2+2)或(0,2﹣2).
一、填空题(每题2分,满分30分).
1.0.01的平方根是 .
2.已知a3=216,那么a= .
3.已知实数a≤0≤b,化简:= .
4.计算:4= .
5.月球沿着一定的轨道围绕地球运动,它的半长轴约为385000千米,这个数据用科学记数法精确到万位表示,应记为 千米.
6.对于近似数0.0680,它有 个有效数字.
7.在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 .
8.在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= .
9.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 度.
10.如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是 .
11.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 度.
12.已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 cm.
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
14.已知△ABC中,AB=AC,∠B=50°,如果D是边BC的中点,那么∠CAD= 度.
15.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 .
二、选择题:(本大题共5题,每小题2分,满分10分)
16.如图,数轴上点P表示的数可能是( )
A.﹣ B. C.﹣3.7 D.﹣
17.下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
18.若∠A,∠B互为补角,且∠A<∠B,则∠A的余角是( )
A.(∠A+∠B) B.∠B C.(∠B﹣∠A) D.∠A
19.在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
20.早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
三、简答题:(本大题共6题,每小题5分,满分30分)
21.计算:(2﹣)0+()﹣1﹣.
22.计算:(﹣+3)×﹣÷.
23.用幂的性质计算:(5﹣17)?(5+17).
24.计算:×÷.
25.如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( ),
∴ = ( ).
∵∠2=∠3(已知),
∴ = ( ).
∴DE∥BC( ),
∴∠EDB+∠DBC=180°( ).
26.平面直角坐标系中,点A(x,y),如果x的两个平方根分别是2y﹣3与1﹣y.
(1)求点A(x,y)的坐标;
(2)点A(x,y)沿x轴的方向向右平移多少个单位后落在第一和第三象限的平分线上?
四、解答题(本大题共4小题,其中27-29每题7分,第30题9分,满分30分)
27.如图,已知△ABC的三个顶点的坐标分别是A(﹣2,3),B(0,1),C(2,2).
(1)在所给的平面直角坐标系中画出△ABC;
(2)求出△ABC的面积;如果点P的坐标为(4,0),请直接判断△PAC和△ABC的面积是否相等.
28.如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
29.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
30.如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
参考答案
一、填空题(每题2分,满分30分)
1.0.01的平方根是 ±0.1 .
【分析】根据平方根的定义即可求出答案.
解:0.01的平方根是±0.1,
故答案为:±0.1;
2.已知a3=216,那么a= 6 .
【分析】根据立方根的定义解答即可.
解:因为a3=216,
所以a==6.
故答案为:6.
3.已知实数a≤0≤b,化简:= b﹣a .
【分析】直接利用a,b的符号得出a﹣b<0,再利用二次根式的性质化简即可.
解:∵a≤0≤b,
∴a﹣b<0,
∴=|a﹣b|=b﹣a.
故答案为:b﹣a.
4.计算:4= .
【分析】幂的n次方公式:(am)n=amn,
解:因为4=22,所以
5.月球沿着一定的轨道围绕地球运动,它的半长轴约为385000千米,这个数据用科学记数法精确到万位表示,应记为 3.9×105 千米.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
解:将385000千米用科学记数法精确到万位表示,应记为3.9×105.
故答案是:3.9×105.
6.对于近似数0.0680,它有 3 个有效数字.
【分析】一个近似数的有效数字是从左边第一个不是0的数字起,后面所有的数字都是这个数的有效数字.
解:近似数0.0680的有效数字是6,8,0,共有3个.
故答案是:3.
7.在平面直角坐标系中,经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线 y=4 .
【分析】垂直于y轴的直线,纵坐标相等为4,所以为直线:y=4.
解:由题意得:经过点A(﹣3,4)且垂直于y轴的直线可以表示为直线为:y=4,
故答案为:y=4.
8.在平面直角坐标系中,如果点Q(a+1,2﹣a)在x轴上,那么a= 2 .
【分析】直接利用x轴上点的坐标特点得出2﹣a=0,进而求出a的值.
解:∵点Q(a+1,2﹣a)在x轴上,
∴2﹣a=0,
解得:a=2.
故答案为:2.
9.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 25 度.
【分析】根据对顶角相等和角平分线的定义可得答案.
解:∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD,
又∵∠ACO=∠BOD,
∴∠BOE=∠AOC=×50°=25°,
故答案为:25.
10.如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是 同位角相等,两直线平行 .
【分析】根据同位角相等两直线平行判断即可.
解:如图,
∵∠BEF=∠DFG,
∴AB∥CD(同位角相等两直线平行),
故答案为:同位角相等两直线平行.
11.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 46 度.
【分析】根据平行线的性质及可得到答案.
解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=126°,∠2=80°,
∴∠3=∠1﹣∠2=46°,
故答案为:46.
12.已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 17 cm.
【分析】根据题意分两种情况:第一种是底边长为7时构不成三角形要排除,第二种情况是底边长为3,然后再将三边长相加即可求得答案.
解:∵等腰三角形的两条边长分别是3cm、7cm,
∴当此三角形的腰长为3cm时,3+3<7,不能构成三角形,故排除,
∴此三角形的腰长为7cm,底边长为3cm,
∴此等腰三角形的周长=7+7+3=17cm,
故答案为:17.
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 90 度.
【分析】连接BD,根据三角形内角和定理求出∠CBD+∠CDB,根据平行线的性质求出∠ABD+∠EDB,即可求出答案.
解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)
=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)
=360°﹣(90°+180°)
=90°,
故答案为:90.
14.已知△ABC中,AB=AC,∠B=50°,如果D是边BC的中点,那么∠CAD= 40 度.
【分析】首先利用等腰三角形的底角的度数求得另一个底角的度数,然后根据等腰三角形“三线合一”的性质求得答案即可.
解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∵D是边BC的中点,
∴AD⊥BC,
∴∠CAD=40°,
故答案为:40.
15.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为 ﹣1或0 .
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.
解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
二、选择题:(本大题共5题,每小题2分,满分10分)
16.如图,数轴上点P表示的数可能是( )
A.﹣ B. C.﹣3.7 D.﹣
【分析】根据数轴上点的位置及无理数的估算进行判断.
解:设点P表示的数为a,
由题意可得:﹣3<a<﹣2,
∵﹣3.7<﹣3<﹣<﹣2<﹣<,
∴选项A符合题意,
故选:A.
17.下列说法正确的是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等边三角形都全等
【分析】根据选项中的说法可以判断两个三角形是否全等,从而可以解答本题.
解:周长相等的锐角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项A错误;
周长相等的直角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项B错误;
周长相等的钝角三角形不一定全等,因为周长相等,三条边不一定对应相等,故选项C错误;
周长相等的等边三角形一定全等,因为周长相等,三条边一定对应相等,利用SSS,可以说明两个三角形全等,故选项D正确;
故选:D.
18.若∠A,∠B互为补角,且∠A<∠B,则∠A的余角是( )
A.(∠A+∠B) B.∠B C.(∠B﹣∠A) D.∠A
【分析】根据互为补角的和得到∠A,∠B的关系式,再根据互为余角的和等于90°表示出∠A的余角,然后把常数消掉整理即可得解.
解:根据题意得,∠A+∠B=180°,
∴∠A的余角为:90°﹣∠A=﹣∠A,
=(∠A+∠B)﹣∠A,
=(∠B﹣∠A).
故选:C.
19.在平面直角坐标系第四象限中到x轴和y轴的距离分别是2、5的点的坐标为( )
A.(5,﹣2) B.(2,﹣5) C.(﹣5,2) D.(﹣2,﹣5)
【分析】根据第四象限点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
解:∵点B在第四象限,且到x轴的距离为2,到y轴的距离为5,
∴点B的横坐标为5,纵坐标为﹣2,
∴点B的坐标为(5,﹣2).
故选:A.
20.早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( )
A.8点23分 B.8点25分 C.8点27分 D.9点整
【分析】根据分针旋转的速度乘分针旋转的时间,可得分针的旋转角,根据秒针旋转的速度成秒针旋转的时间,可得秒针的旋转角,根据分针的旋转角减去秒针的旋转角,可得答案.
解:设t分后时钟的分针和时针第一次垂直,依题意有
6t﹣0.5t=360﹣120﹣90,
解得t=27.
故早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是8点27分.
故选:C.
三、简答题:(本大题共6题,每小题5分,满分30分)
21.计算:(2﹣)0+()﹣1﹣.
【分析】根据零指数幂的意义,二次根式的加减运算以及乘除运算即可求出答案.
解:原式=1+﹣|2﹣|
=1+﹣(2﹣)
=1+﹣2+
=2﹣1.
22.计算:(﹣+3)×﹣÷.
【分析】根据二次根式的加减运算以及乘除运算即可求出答案.
解:原式=﹣2+3×2﹣
=﹣2+6﹣2
=2.
23.用幂的性质计算:(5﹣17)?(5+17).
【分析】平方差公式:(a+b)(a﹣b)=a2﹣b2,题中数据与公式对应:a=5,b=,a2=52=25,b2=()2=17×=171=17
解:原式=[(5﹣)(5+)]
=(25﹣17)
=8
=
=2
24.计算:×÷.
【分析】直接利用分数指数幂的性质将原式变形计算得出答案.
解:原式=2×2÷2
=2
=22
=4.
25.如图,已知在△ABC中,FG∥EB,∠2=∠3,说明∠EDB+∠DBC=180°的理由.
解:∵FG∥EB( 已知 ),
∴ ∠1 = ∠2 ( 两直线平行,同位角相等 ).
∵∠2=∠3(已知),
∴ ∠1 = ∠3 ( 等量代换 ).
∴DE∥BC( 内错角相等,两直线平行 ),
∴∠EDB+∠DBC=180°( 两直线平行,同旁内角互补 ).
【分析】利用平行线的性质和判定解答即可
解:∵FG∥EB(已知),
∴∠1=∠2(两直线平行,同位角相等).
∵∠2=∠3(已知),
∴∠1=∠3(等量代换).
∴DE∥BC(内错角相等,两直线平行).
∴∠EDB+∠DBC=180°(两直线平行,同旁内角互补).
故答案为:已知;∠1;∠2;两直线平行,同位角相等;∠1;∠3;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补.
26.平面直角坐标系中,点A(x,y),如果x的两个平方根分别是2y﹣3与1﹣y.
(1)求点A(x,y)的坐标;
(2)点A(x,y)沿x轴的方向向右平移多少个单位后落在第一和第三象限的平分线上?
【分析】(1)根据平方根的概念得出y的方程,进而解答即可;
(2)根据平移的性质解答即可.
解:(1)根据题意得:(2y﹣3)+(1﹣y)=0,
解得:y=2,
可得:x=(2y﹣3)2=1,
所求的点A的坐标为A(1,2);
(2)根据题意得:(1,2)→(2,2),
点A(1,2)沿x轴的方向向右平移1个单位后落在第一和第三象限的平分线上.
四、解答题(本大题共4小题,其中27-29每题7分,第30题9分,满分30分)
27.如图,已知△ABC的三个顶点的坐标分别是A(﹣2,3),B(0,1),C(2,2).
(1)在所给的平面直角坐标系中画出△ABC;
(2)求出△ABC的面积;如果点P的坐标为(4,0),请直接判断△PAC和△ABC的面积是否相等.
【分析】(1)根据A,B,C的坐标作出A,B,C三点即可.
(2)利用分割法把三角形面积转化为矩形面积减去三个三角形面积即可,再利用等高模型解决问题.
解:(1)如图,△ABC即为所求.
(2)连接PB.
S△ABC=2×4﹣×2×2﹣×1×4﹣×1×2=3.
∵PB∥AC,
∴S△PAC=S△ABC.
28.如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
【分析】根据BD=DC得出∠DBC=∠DCB,进而利用全等三角形的判定和性质证明即可.
【解答】证明:∵BD=DC,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
29.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
【分析】(1)根据平行线的性质和全等三角形的判定和性质得出△ABD与△CDB全等,进而利用全等三角形的性质解答即可;
(2)根据平行线的性质和全等三角形的判定和性质得出△EFB与△CDB全等,进而解答即可.
解:(1)AD=CB,
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,
∵AD=CB,BE=AD,
∴BC=BE,
∵AD∥BC,
∴∠ADB=∠DBF,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
30.如图,在直角坐标平面内有点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是否是等腰直角三角形?为什么?
(2)课文阅读材料告诉我们,古希腊的希帕斯经过探索,发现了如此情况下AB的长是一个无理数,请你(不用勾股定理等后面所学习的方法)求出AB的长,以此向古代先贤致敬;
(3)点P在y轴上,如果△PAB是等腰三角形,请直接写出点P的坐标.
【分析】(1)由等腰三角形的性质可求∠ABO=∠BAO=45°,∠ACO=∠CAO=45°,可得结论;
(2)由面积法可求AB的长;
(3)分三种情况讨论,由等腰三角形的性质可求解.
解:(1)△ABC是等腰直角三角形,
理由如下:∵点A(0,2)、B(﹣2,0)、C(2,0),
∴OA=OB=OC=2,
又∵∠AOB=∠AOC=90°,
∴∠ABO=∠BAO=45°,∠ACO=∠CAO=45°,
∴∠BAC=90°,∠ABO=∠ACO,
∴AB=AC,
∴△ABC是等腰直角三角形;
(2)∵S△ABC=×AB×AC=×BC×AO,
∴AB2=4×2=8,
∴AB=2,AB=﹣2(舍去),
∴AB的长为2;
(3)若PB=PA,则点P与点O重合,即点P坐标为(0,0);
若BA=BP=2,且OA⊥OB,
∴OA=OP=2,
∴点P(0,﹣2),
若AB=AP=2,且点A(0,2),
∴点P(0,2+2)或(0,2﹣2),
综上所述:点P的坐标为(0,0)或(0,﹣2)或(0,2+2)或(0,2﹣2).
同课章节目录
