五年级上册数学教案 多边形的面积(二) 苏教版
文档属性
| 名称 | 五年级上册数学教案 多边形的面积(二) 苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 90.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 14:45:14 | ||
图片预览


文档简介
多边形的面积(二)
学习目标:
掌握多边形(尤其是梯形)的面积计算公式;
运用多边形面积计算公式解决组合图形问题。
教学重点:
掌握多边形面积(尤其是梯形)的计算公式,并能灵活运用。
教学难点:
组合图形的面积计算
教学过程:
一、情境体验
师:同学们有去三峡玩过吗?你们参观过葛洲坝水利枢纽吗?
学生踊跃回答
师:葛洲坝水利枢纽位于湖北省宜昌市境内的长江三峡末端河段上,距离长江三
峡出口南津关下游2.3公里。它是长江上第一座大型水电站,也是世界上最
大的低水头大流量、径流式水电站。
师:现在请大家观察图片,图中大坝的横截面是什么图形?你们会求它的面积
吗?今天我们就继续来学习多边形的面积(二)——梯形。(板书课题)
首先还是来简单复习上节课学习的多边形周长、面积计算公式以及这些公式的灵活应用。(参考PPT)
3162300265430基础巩固
展示例1
例1:如图:已知三角形的面积是60平方厘米,求梯形(阴影部分)的面积。(单位:厘米)
师:梯形的面积怎么求?
生:面积=(上底+下底)×高÷2。
师:观察图形可知梯形的上底是24厘米,下底知道吗?
生:下底是24+8=32(厘米)。
师:大拇指给你点赞,真聪明!那么,梯形的高是多少呢?你们动手画一画梯形
的高,看看有什么发现。
学生动手画出梯形的高
生:老师,我发现图中画垂直符号的这条竖着的线段正好是梯形的高,也是三角
形的高。
师:的确如此,由图中可以看出:三角形的高和梯形的高是相等的。而三角形的
面积是60平方厘米,底是8厘米,由此可以算出高。高是多少呢?
生:三角形的高=面积×2÷底,60×2÷8=15(厘米)
师:因此梯形的高就是15厘米,所以梯形的面积列式子计算就等于多少?
生:(24+24+8)×15÷2=420(平方厘米)
展示例2
例2:公园里有块梯形绿地,种树20棵。这块地上底是45米,下底是15米,高是12米。每棵树占地多少平方米?
师:已知这块绿地是一个梯形,并且也知道上底、下底和高,我们可以求出什么?
生:可以求出这块绿地的面积。
师:怎么求?你们动手算一算。
生:面积=(上底+下底)×高÷2,(45+15)×12÷2=360(平方米)。
师:现在知道这块绿地的面积是360平方米,种了20棵树,求平均每棵树占
地多少平方米,应该用什么法列式计算?
生:除法,360÷20=18(平方米)
306768549530展示例3
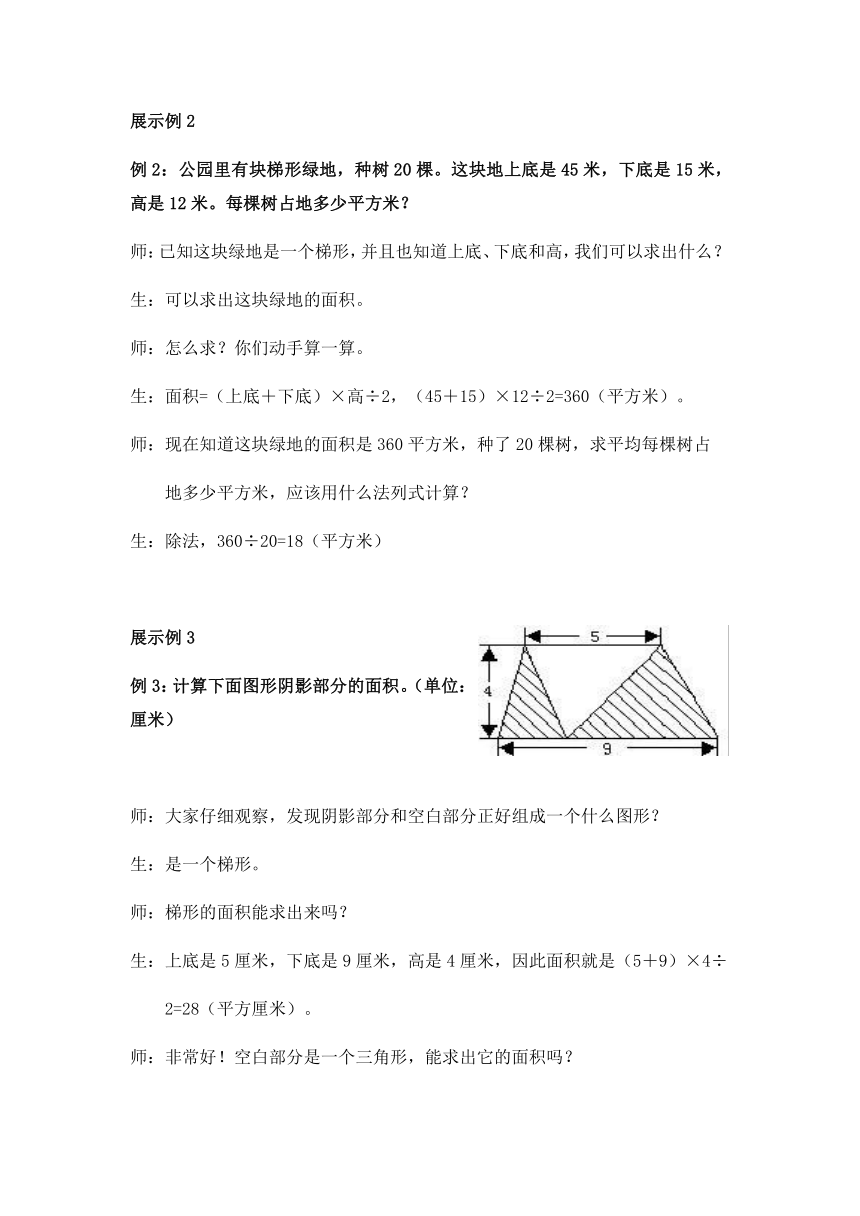
例3:计算下面图形阴影部分的面积。(单位:厘米)
师:大家仔细观察,发现阴影部分和空白部分正好组成一个什么图形?
生:是一个梯形。
师:梯形的面积能求出来吗?
生:上底是5厘米,下底是9厘米,高是4厘米,因此面积就是(5+9)×4÷
2=28(平方厘米)。
师:非常好!空白部分是一个三角形,能求出它的面积吗?
生:底是5厘米,高是4厘米,面积就是5×4÷2=10(平方厘米)。
师:刚才已经得出,阴影部分和空白部分正好组成一个梯形,因此阴影部分面积
就等于梯形面积减去空白部分面积,28-10=18(平方厘米)。
师:同学们再想一想,本题还有没有其他解答方法呢?
师引导:刚才我们是用梯形面积减去空白部分面积,求出阴影部分面积。能不能
直接求阴影面积呢?
学生思考
师:阴影部分是两个三角形,这两个三角形的底之和恰好是梯形的下底9厘米,
而高都是4厘米。左边三角形的面积=底1×4÷2=底1×2,右边三角形的面
积=底2×4÷2=底2×2,因此阴影部分面积就=底1×2+底2×2,利用乘法分
配律逆运算,面积=(底1+底2)×2=9×2=18(平方厘米)
展示例4
例4:下面是用彩纸剪出的大写英文字母T和E,哪个字母用的彩纸面积大?
师:要比较哪个字母用的彩纸面积大,首先要分别求出它们的面积。大家观察这
两个字母图形,是我们学过的规则多边形吗?
生:不是,它们是不规则图形。
师:还记得以前“长方形和正方形” 里学过的巧求面积吗?求不规则图形的面
积,需要用“转化”思想,将不规则图形转化为规则图形,方法是分割法或
添补法。什么是分割法?什么是添补法?
生1:分割法就是把不规则图形分成若干个规则图形;
生2:添补法就是把不规则图形补成规则图形。
师:既然找到了方法,我们先来看字母T,用什么方法求面积?
生:分割法、添补法都可以。
学生动手尝试两种做法,师再集体订正讲解。
同样的,字母E也可以两种方法解答。
师:求出字母T的面积是2000平方厘米,字母E的面积是2448平方厘米,谁用
的彩纸面积大?
生:2448>2000,字母E用的彩纸面积大。
三、综合拓展
展示例5
例5:已知梯形的上底是6厘米,下底是8厘米,阴影部分面积是24平方厘米,求梯形的面积。
师:已知梯形的上底、下底,要求它的面积,还需要知道什么?
生:还要知道梯形的高。
师:仔细观察梯形和阴影三角形,发现它们的高有什么特点呢?
学生思考
生:哦,我发现如果阴影三角形以6厘米为底,它的高和梯形的高就相等。
师:你真是个聪明的小观察家!题目已告诉我们阴影三角形的面积是24平方厘
米,底是6厘米,因此高怎么计算?
生:三角形的高=面积×2÷底,24×2÷6=8(厘米)
师:梯形和三角形的高相等,为8厘米,所以梯形的面积列式子计算就是?
生:(6+8)×8÷2=56(平方厘米)
展示例6
例6:一堆钢管堆放成梯形,最上层16根,最下层24根,有9层。这堆钢管共有多少根?
师:梯形的面积计算公式是什么?
生:面积=(上底+下底)×高÷2。
师:一堆钢管堆放成梯形,最上层16根,就是梯形的上底,最下层24根,是梯
形的下底,有9层,是梯形的高。可以利用梯形的面积计算公式,求出这堆
钢管共多少根。你们动手算一算吧。
生:(16+24)×9÷2=180(根)
师:是的,注意最后不要忘记除以2。
五、总结
通过今天的学习,你有哪些收获?
学习目标:
掌握多边形(尤其是梯形)的面积计算公式;
运用多边形面积计算公式解决组合图形问题。
教学重点:
掌握多边形面积(尤其是梯形)的计算公式,并能灵活运用。
教学难点:
组合图形的面积计算
教学过程:
一、情境体验
师:同学们有去三峡玩过吗?你们参观过葛洲坝水利枢纽吗?
学生踊跃回答
师:葛洲坝水利枢纽位于湖北省宜昌市境内的长江三峡末端河段上,距离长江三
峡出口南津关下游2.3公里。它是长江上第一座大型水电站,也是世界上最
大的低水头大流量、径流式水电站。
师:现在请大家观察图片,图中大坝的横截面是什么图形?你们会求它的面积
吗?今天我们就继续来学习多边形的面积(二)——梯形。(板书课题)
首先还是来简单复习上节课学习的多边形周长、面积计算公式以及这些公式的灵活应用。(参考PPT)
3162300265430基础巩固
展示例1
例1:如图:已知三角形的面积是60平方厘米,求梯形(阴影部分)的面积。(单位:厘米)
师:梯形的面积怎么求?
生:面积=(上底+下底)×高÷2。
师:观察图形可知梯形的上底是24厘米,下底知道吗?
生:下底是24+8=32(厘米)。
师:大拇指给你点赞,真聪明!那么,梯形的高是多少呢?你们动手画一画梯形
的高,看看有什么发现。
学生动手画出梯形的高
生:老师,我发现图中画垂直符号的这条竖着的线段正好是梯形的高,也是三角
形的高。
师:的确如此,由图中可以看出:三角形的高和梯形的高是相等的。而三角形的
面积是60平方厘米,底是8厘米,由此可以算出高。高是多少呢?
生:三角形的高=面积×2÷底,60×2÷8=15(厘米)
师:因此梯形的高就是15厘米,所以梯形的面积列式子计算就等于多少?
生:(24+24+8)×15÷2=420(平方厘米)
展示例2
例2:公园里有块梯形绿地,种树20棵。这块地上底是45米,下底是15米,高是12米。每棵树占地多少平方米?
师:已知这块绿地是一个梯形,并且也知道上底、下底和高,我们可以求出什么?
生:可以求出这块绿地的面积。
师:怎么求?你们动手算一算。
生:面积=(上底+下底)×高÷2,(45+15)×12÷2=360(平方米)。
师:现在知道这块绿地的面积是360平方米,种了20棵树,求平均每棵树占
地多少平方米,应该用什么法列式计算?
生:除法,360÷20=18(平方米)
306768549530展示例3
例3:计算下面图形阴影部分的面积。(单位:厘米)
师:大家仔细观察,发现阴影部分和空白部分正好组成一个什么图形?
生:是一个梯形。
师:梯形的面积能求出来吗?
生:上底是5厘米,下底是9厘米,高是4厘米,因此面积就是(5+9)×4÷
2=28(平方厘米)。
师:非常好!空白部分是一个三角形,能求出它的面积吗?
生:底是5厘米,高是4厘米,面积就是5×4÷2=10(平方厘米)。
师:刚才已经得出,阴影部分和空白部分正好组成一个梯形,因此阴影部分面积
就等于梯形面积减去空白部分面积,28-10=18(平方厘米)。
师:同学们再想一想,本题还有没有其他解答方法呢?
师引导:刚才我们是用梯形面积减去空白部分面积,求出阴影部分面积。能不能
直接求阴影面积呢?
学生思考
师:阴影部分是两个三角形,这两个三角形的底之和恰好是梯形的下底9厘米,
而高都是4厘米。左边三角形的面积=底1×4÷2=底1×2,右边三角形的面
积=底2×4÷2=底2×2,因此阴影部分面积就=底1×2+底2×2,利用乘法分
配律逆运算,面积=(底1+底2)×2=9×2=18(平方厘米)
展示例4
例4:下面是用彩纸剪出的大写英文字母T和E,哪个字母用的彩纸面积大?
师:要比较哪个字母用的彩纸面积大,首先要分别求出它们的面积。大家观察这
两个字母图形,是我们学过的规则多边形吗?
生:不是,它们是不规则图形。
师:还记得以前“长方形和正方形” 里学过的巧求面积吗?求不规则图形的面
积,需要用“转化”思想,将不规则图形转化为规则图形,方法是分割法或
添补法。什么是分割法?什么是添补法?
生1:分割法就是把不规则图形分成若干个规则图形;
生2:添补法就是把不规则图形补成规则图形。
师:既然找到了方法,我们先来看字母T,用什么方法求面积?
生:分割法、添补法都可以。
学生动手尝试两种做法,师再集体订正讲解。
同样的,字母E也可以两种方法解答。
师:求出字母T的面积是2000平方厘米,字母E的面积是2448平方厘米,谁用
的彩纸面积大?
生:2448>2000,字母E用的彩纸面积大。
三、综合拓展
展示例5
例5:已知梯形的上底是6厘米,下底是8厘米,阴影部分面积是24平方厘米,求梯形的面积。
师:已知梯形的上底、下底,要求它的面积,还需要知道什么?
生:还要知道梯形的高。
师:仔细观察梯形和阴影三角形,发现它们的高有什么特点呢?
学生思考
生:哦,我发现如果阴影三角形以6厘米为底,它的高和梯形的高就相等。
师:你真是个聪明的小观察家!题目已告诉我们阴影三角形的面积是24平方厘
米,底是6厘米,因此高怎么计算?
生:三角形的高=面积×2÷底,24×2÷6=8(厘米)
师:梯形和三角形的高相等,为8厘米,所以梯形的面积列式子计算就是?
生:(6+8)×8÷2=56(平方厘米)
展示例6
例6:一堆钢管堆放成梯形,最上层16根,最下层24根,有9层。这堆钢管共有多少根?
师:梯形的面积计算公式是什么?
生:面积=(上底+下底)×高÷2。
师:一堆钢管堆放成梯形,最上层16根,就是梯形的上底,最下层24根,是梯
形的下底,有9层,是梯形的高。可以利用梯形的面积计算公式,求出这堆
钢管共多少根。你们动手算一算吧。
生:(16+24)×9÷2=180(根)
师:是的,注意最后不要忘记除以2。
五、总结
通过今天的学习,你有哪些收获?
