2.2.1综合法与分析法1
图片预览




文档简介
(共19张PPT)
2.2直接证明与间接证明
2.2.1 综合法和分析法(1)
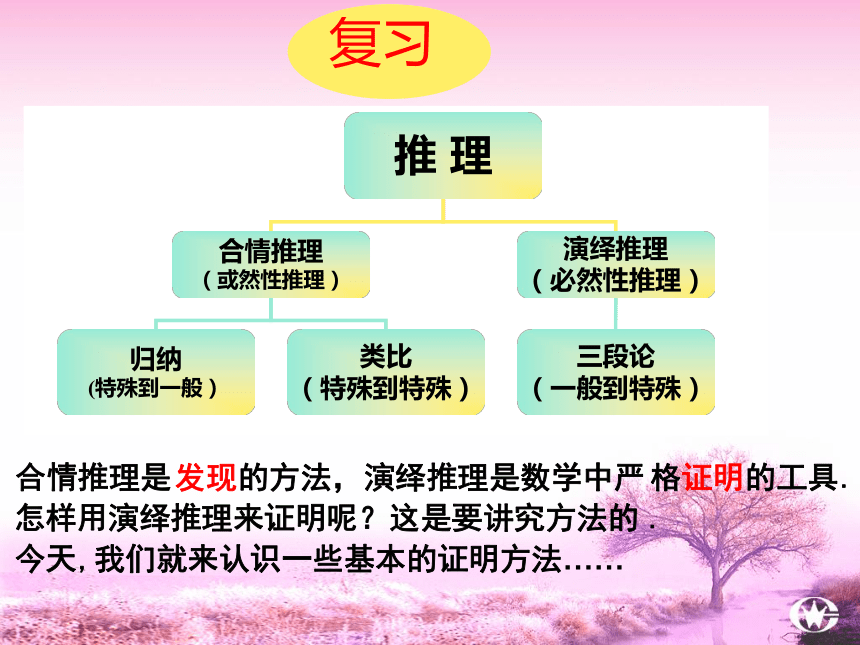
复习
推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
合情推理是
发现
的方法,
演绎推理是数学中严
格
证明
的工具
.
怎样用演绎推理来证明呢?这是要讲究方法的
.
今天
,
我们就来认识一些基本的证明方法……
合情推理得到的结论是不可靠的,需要证明。数学中证明的方法有哪些呢?
例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.
因此a(b2+c2)+b(c2+a2)≥4abc.
证明:
在数学证明中,我们经常从已知条件和某些数学定义、定理、公理、性质等出发通过推理导出所要的结论。
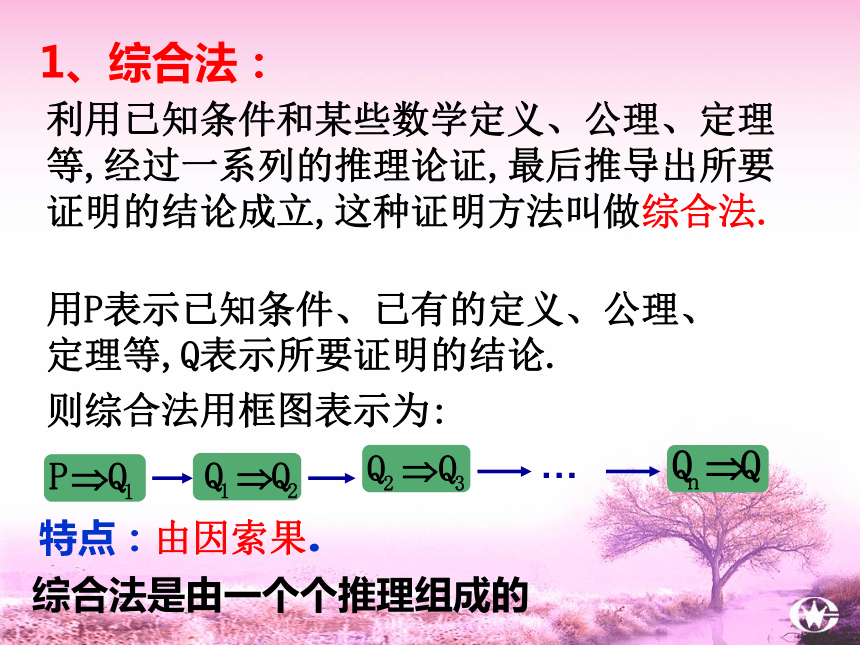
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
1、综合法:
综合法是由一个个推理组成的
特点:由因索果.
直接证明
1 概念
直接从原命题的条件逐步推得命题成立
2 直接证明的一般形式:
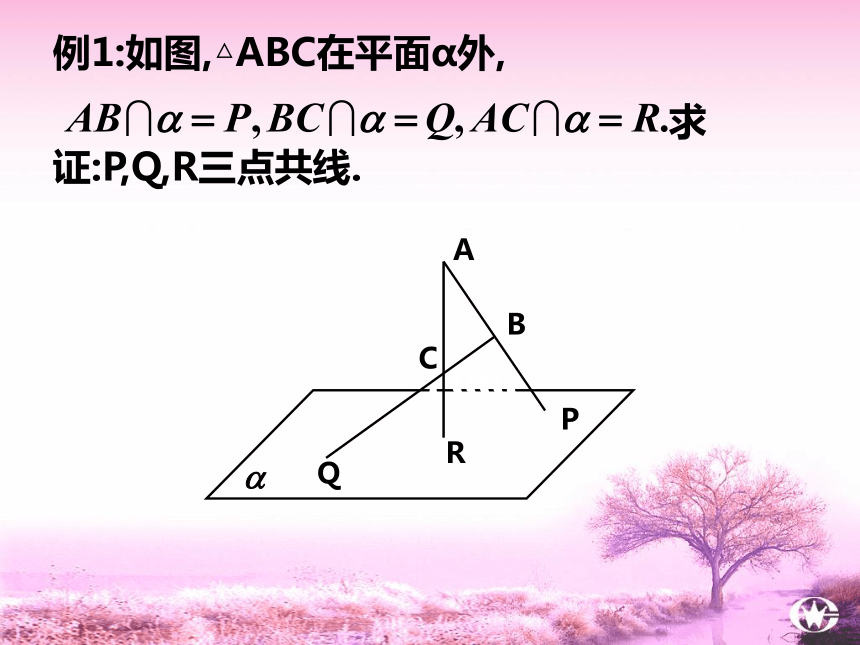
例1:如图,△ABC在平面α外,
求证:P,Q,R三点共线.
A
B
C
P
Q
R
分析:立体几何中证明三点共线或三线共点一般要用公理2。公理2的内容是什么
此题要证明三点共线,需要说明这三点均在一个平面上,则这三点一定在交线上。
证明:
(1)
(2)
分析:由已知条件和结论我们联想到数量积定义和
三解形的面积公式:
由数量积定义和上公式结合结论探求证明思路
证明:
例3:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证:△ABC为等边三角形.
符号语言
图形语言
文字语言
学会语言转换
找出隐含条件
证明:
由A,B,C成等差数列,有
2B=A+C ①
由①②,得
②
③
由啊,a,b,c成等比数列,有
④
由余弦定理及③,可得
再由④,得
因此,a=c
从而有 A=C
由②③⑤,得
【巩固练习】
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
小结
综合法的定义:
2.2直接证明与间接证明
2.2.1 综合法和分析法(1)
复习
推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
合情推理是
发现
的方法,
演绎推理是数学中严
格
证明
的工具
.
怎样用演绎推理来证明呢?这是要讲究方法的
.
今天
,
我们就来认识一些基本的证明方法……
合情推理得到的结论是不可靠的,需要证明。数学中证明的方法有哪些呢?
例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.
因此a(b2+c2)+b(c2+a2)≥4abc.
证明:
在数学证明中,我们经常从已知条件和某些数学定义、定理、公理、性质等出发通过推理导出所要的结论。
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
1、综合法:
综合法是由一个个推理组成的
特点:由因索果.
直接证明
1 概念
直接从原命题的条件逐步推得命题成立
2 直接证明的一般形式:
例1:如图,△ABC在平面α外,
求证:P,Q,R三点共线.
A
B
C
P
Q
R
分析:立体几何中证明三点共线或三线共点一般要用公理2。公理2的内容是什么
此题要证明三点共线,需要说明这三点均在一个平面上,则这三点一定在交线上。
证明:
(1)
(2)
分析:由已知条件和结论我们联想到数量积定义和
三解形的面积公式:
由数量积定义和上公式结合结论探求证明思路
证明:
例3:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证:△ABC为等边三角形.
符号语言
图形语言
文字语言
学会语言转换
找出隐含条件
证明:
由A,B,C成等差数列,有
2B=A+C ①
由①②,得
②
③
由啊,a,b,c成等比数列,有
④
由余弦定理及③,可得
再由④,得
因此,a=c
从而有 A=C
由②③⑤,得
【巩固练习】
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
小结
综合法的定义:
