抛物线及其标准方程
图片预览





文档简介
(共19张PPT)
课题:
抛物线及其标准方程
复习:
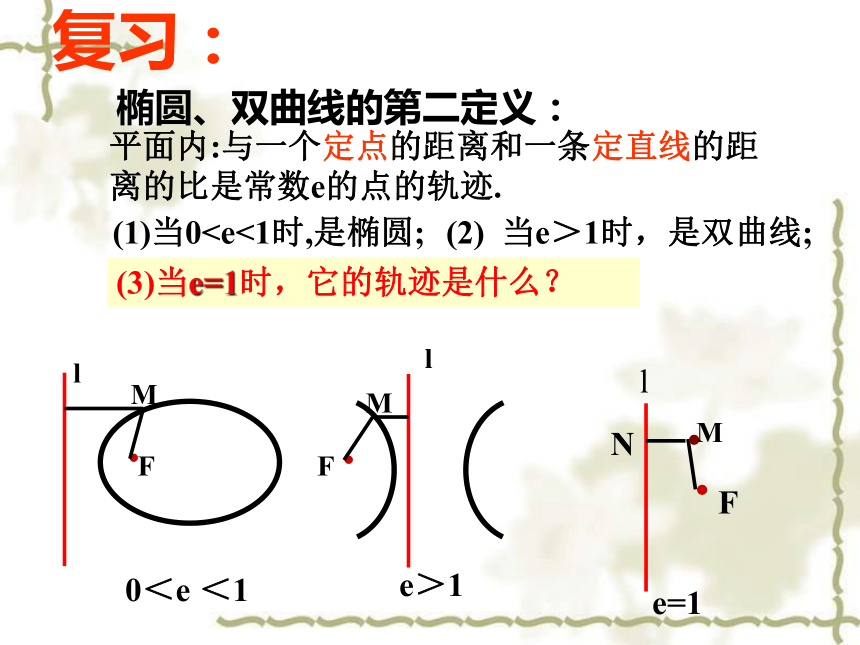
椭圆、双曲线的第二定义:
平面内:与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
·
M
F
l
0<e <1
l
F
·
M
e>1
(2) 当e>1时,是双曲线;
(1)当0(3)当e=1时,它的轨迹是什么?
·
F
N
e=1
·
M
l
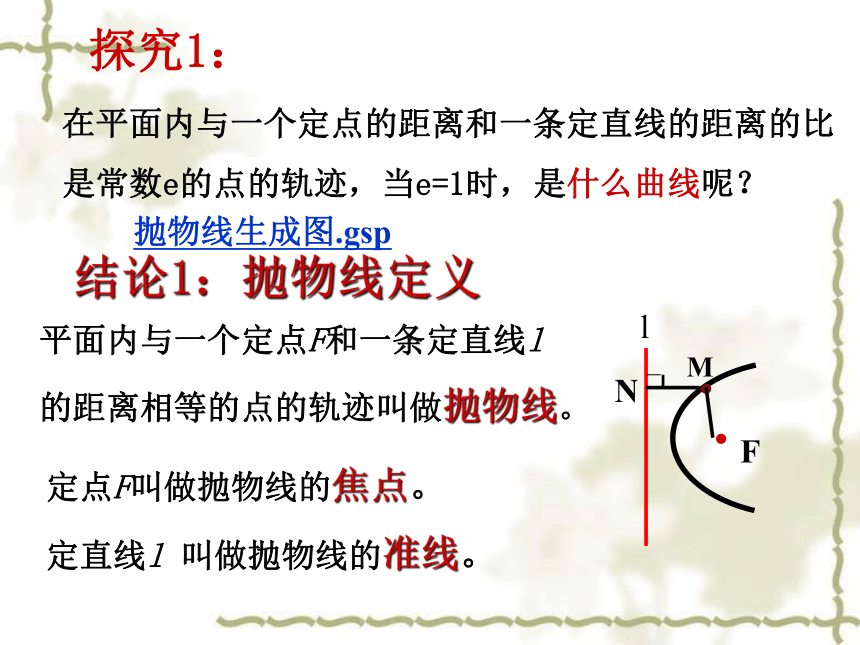
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
结论1:抛物线定义
·
·
F
M
l
N
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
探究1:
在平面内与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,当e=1时,是什么曲线呢?
抛物线生成图.gsp
探究2:如何求这种抛物线的方程呢?
x
y
o
·
·
F
M
l
N
K
设︱KF︱= p
则F( ,0),l:x = -
p
2
p
2
设点M的坐标为(x,y),
由定义可知,
化简得 y2 = 2px(p>0)
取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴
其中 p 为正常数,它的几何意义是:
焦点到准线的距离(焦准距)
结论2:抛物线的标准方程:
y
o
x
·
·
F
M
l
N
K
想一想:抛物线的标准方程还有几种不同的形式 它们是如何建系的
方程 y2 = 2px(p>0)叫做抛物线的标准方程。其中焦点 坐标准线方程是
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形 焦 点 准 线 标准方程
想一想:由上表中抛物线的标准方程的不同形式与图形、焦点坐标、准线方程对应关系,如何判断抛物线的焦点位置和开口方向?
第一:一次项的变量如为X(或Y),则
X轴(或Y轴)为抛物线的对称轴,焦点
就在对称轴上。
第二:一次项系数的正负决定了开口方向!
例题1
准线方程是:
已知抛物线的标准方程是
求它的焦点坐标及准线方程.
y
x
o
3
;
6
2
=
=
p
p
解:
变题1
已知抛物线的标准方程是
求它的焦点坐标及准线方程.
o
y
x
准线方程是:
3
;
6
2
=
=
p
p
解:
例题2:已知抛物线的焦点坐标是F(0,-2),
求它的标准方程
解:因为焦点在y轴的负半轴上,并且
所以所求抛物线的标准方程是
变题2:已知抛物线顶点在原点,对称轴为坐标轴,焦点在直线 上,求它的标准方程.
变题3、求过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
当焦点在x轴的负半轴上时,
把A(-3,2)
代入y2 = -2px,得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程是 ;
(3)焦点到准线的距离是2。
学生活动
2、求下列抛物线的焦点坐标和准线方程:
(3)
(4)
(2)
(1)
准线方程
焦点坐标
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
y=2
(0 , -2)
拓展提高
1、 有一点 ,求点M到焦点的距离。
2、若抛物线 上有一点M,若点
M的横坐标为9,它到焦点的距离是10,求抛
物线方程和M点的坐标。
小 结 :
1、抛物线的定义,四种标准方程的形式,p的几何意义
2、求抛物线的标准方程和它的焦点坐标、准线方程
3、用坐标法求标准方程
课堂作业:
课本 P133: 1、2、4
Thank you!
课题:
抛物线及其标准方程
复习:
椭圆、双曲线的第二定义:
平面内:与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
·
M
F
l
0<e <1
l
F
·
M
e>1
(2) 当e>1时,是双曲线;
(1)当0
·
F
N
e=1
·
M
l
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
结论1:抛物线定义
·
·
F
M
l
N
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
探究1:
在平面内与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,当e=1时,是什么曲线呢?
抛物线生成图.gsp
探究2:如何求这种抛物线的方程呢?
x
y
o
·
·
F
M
l
N
K
设︱KF︱= p
则F( ,0),l:x = -
p
2
p
2
设点M的坐标为(x,y),
由定义可知,
化简得 y2 = 2px(p>0)
取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴
其中 p 为正常数,它的几何意义是:
焦点到准线的距离(焦准距)
结论2:抛物线的标准方程:
y
o
x
·
·
F
M
l
N
K
想一想:抛物线的标准方程还有几种不同的形式 它们是如何建系的
方程 y2 = 2px(p>0)叫做抛物线的标准方程。其中焦点 坐标准线方程是
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形 焦 点 准 线 标准方程
想一想:由上表中抛物线的标准方程的不同形式与图形、焦点坐标、准线方程对应关系,如何判断抛物线的焦点位置和开口方向?
第一:一次项的变量如为X(或Y),则
X轴(或Y轴)为抛物线的对称轴,焦点
就在对称轴上。
第二:一次项系数的正负决定了开口方向!
例题1
准线方程是:
已知抛物线的标准方程是
求它的焦点坐标及准线方程.
y
x
o
3
;
6
2
=
=
p
p
解:
变题1
已知抛物线的标准方程是
求它的焦点坐标及准线方程.
o
y
x
准线方程是:
3
;
6
2
=
=
p
p
解:
例题2:已知抛物线的焦点坐标是F(0,-2),
求它的标准方程
解:因为焦点在y轴的负半轴上,并且
所以所求抛物线的标准方程是
变题2:已知抛物线顶点在原点,对称轴为坐标轴,焦点在直线 上,求它的标准方程.
变题3、求过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
当焦点在x轴的负半轴上时,
把A(-3,2)
代入y2 = -2px,得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程是 ;
(3)焦点到准线的距离是2。
学生活动
2、求下列抛物线的焦点坐标和准线方程:
(3)
(4)
(2)
(1)
准线方程
焦点坐标
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
y=2
(0 , -2)
拓展提高
1、 有一点 ,求点M到焦点的距离。
2、若抛物线 上有一点M,若点
M的横坐标为9,它到焦点的距离是10,求抛
物线方程和M点的坐标。
小 结 :
1、抛物线的定义,四种标准方程的形式,p的几何意义
2、求抛物线的标准方程和它的焦点坐标、准线方程
3、用坐标法求标准方程
课堂作业:
课本 P133: 1、2、4
Thank you!
