平行四边形性质(二)
图片预览


文档简介
(共20张PPT)
数学八年级下册
2.上节课我们掌握了平行四边
形的哪些性质?
1.什么是平行四边形?
复习
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
2.记作:
ABCD
3.读作:平行四边形ABCD
A
B
C
D
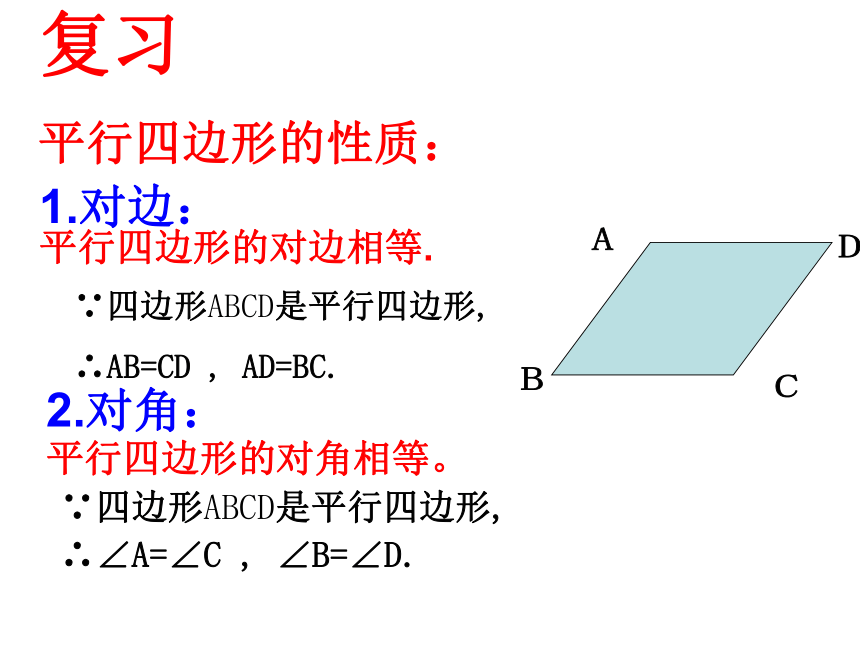
复行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等。
1.对边:
2.对角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
复习
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
O
A
B
C
D
(C)
(A)
(B)
(D)
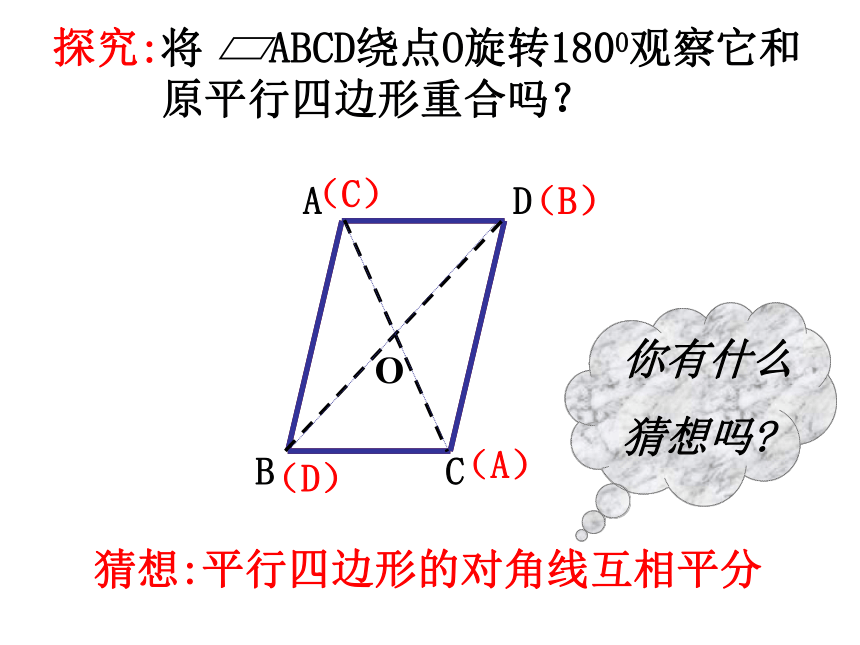
探究:将 ABCD绕点O旋转1800观察它和
原平行四边形重合吗?
猜想:平行四边形的对角线互相平分
你有什么
猜想吗
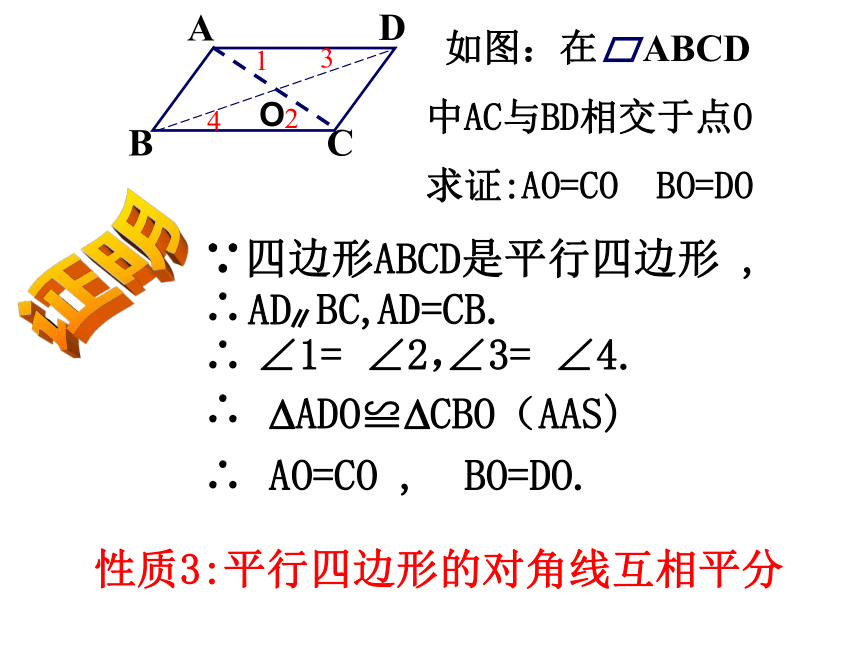
如图:在
中AC与BD相交于点O
求证:AO=CO BO=DO
ABCD
A
B
C
D
1
2
3
4
O
AD
BC,
∠1= ∠2,
∠3= ∠4.
∵四边形ABCD是平行四边形 ,
ADO≌ CBO(AAS)
AD=CB.
AO=CO , BO=DO.
∴
∴
∴
∴
性质3:平行四边形的对角线互相平分
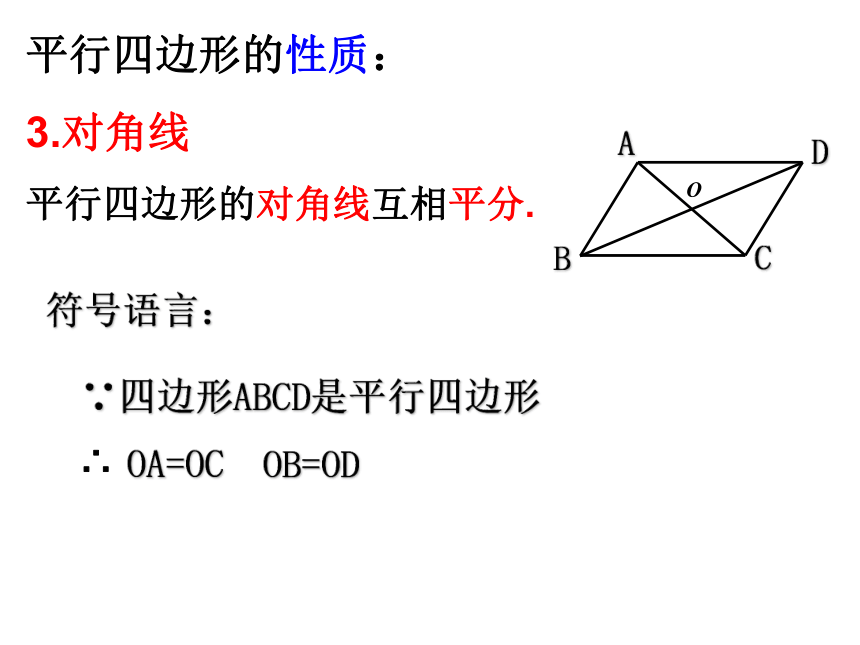
平行四边形的性质:
3.对角线
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
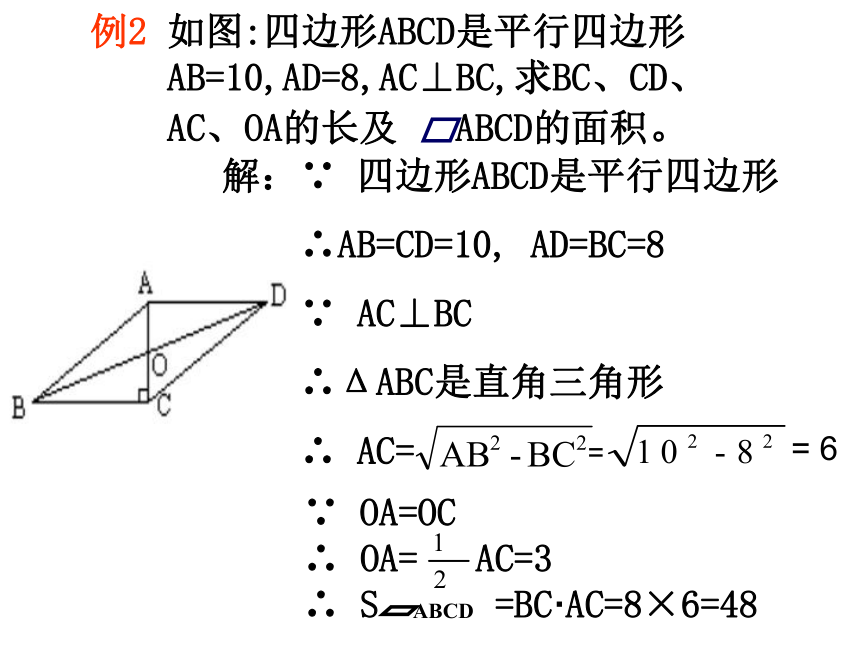
解:∵ 四边形ABCD是平行四边形
∴AB=CD=10, AD=BC=8
∵ AC⊥BC
∴ΔABC是直角三角形
∴ AC=
=
= 6
∵ OA=OC
∴ OA= AC=3
∴ S =BC·AC=8×6=48
ABCD
例2 如图:四边形ABCD是平行四边形
AB=10,AD=8,AC⊥BC,求BC、CD、
AC、OA的长及 ABCD的面积。
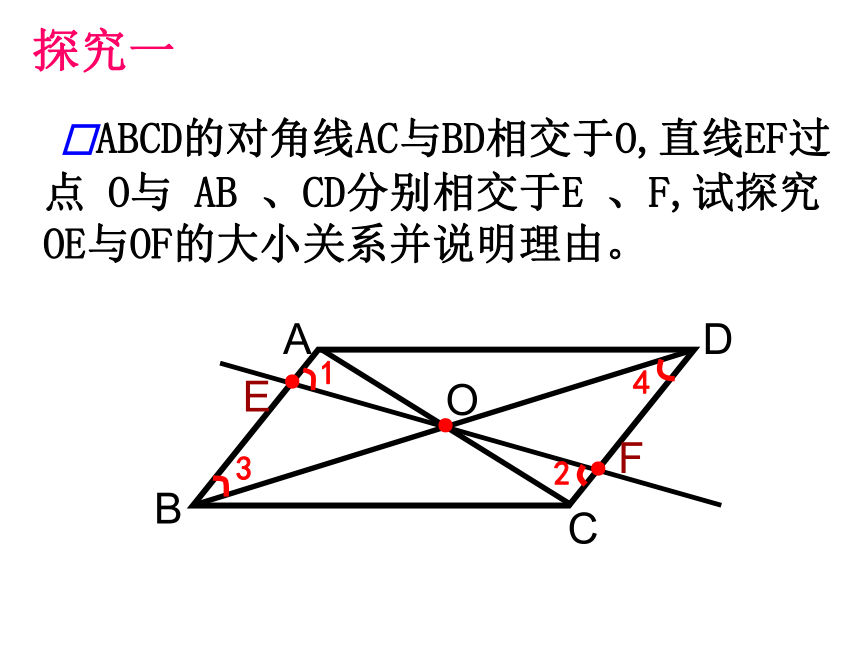
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究一
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下
图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
A
B
C
D
如图,在 ABCD中,
BC=10cm, AC=8cm, BD=14cm,
(1)△ BOC的周长是多少?
说明理由?
( 2) △ ABC与△ DBC的周长哪个长,
长多少?
A
B
D
C
O
若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
O
D
B
A
C
D
O
D
B
A
C
如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,
则CD=______.
5
如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
O
D
B
A
C
●
1<AD<9
公园有一片绿地,它的形状是平行四边形
绿地上要修几条笔直的小路,如图,AB=15cm
AD=12cm,AC⊥BC,求小路 BC,CD,OC的长
并算出绿地的面积.
课堂作业:
课本91页练习第3题,第6题。
家庭作业:
大册子39-40页《平行四边形性质(2)》
数学八年级下册
2.上节课我们掌握了平行四边
形的哪些性质?
1.什么是平行四边形?
复习
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
2.记作:
ABCD
3.读作:平行四边形ABCD
A
B
C
D
复行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等。
1.对边:
2.对角:
∵四边形ABCD是平行四边形,
∴∠A=∠C , ∠B=∠D.
复习
∵四边形ABCD是平行四边形,
∴AB=CD , AD=BC.
O
A
B
C
D
(C)
(A)
(B)
(D)
探究:将 ABCD绕点O旋转1800观察它和
原平行四边形重合吗?
猜想:平行四边形的对角线互相平分
你有什么
猜想吗
如图:在
中AC与BD相交于点O
求证:AO=CO BO=DO
ABCD
A
B
C
D
1
2
3
4
O
AD
BC,
∠1= ∠2,
∠3= ∠4.
∵四边形ABCD是平行四边形 ,
ADO≌ CBO(AAS)
AD=CB.
AO=CO , BO=DO.
∴
∴
∴
∴
性质3:平行四边形的对角线互相平分
平行四边形的性质:
3.对角线
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
解:∵ 四边形ABCD是平行四边形
∴AB=CD=10, AD=BC=8
∵ AC⊥BC
∴ΔABC是直角三角形
∴ AC=
=
= 6
∵ OA=OC
∴ OA= AC=3
∴ S =BC·AC=8×6=48
ABCD
例2 如图:四边形ABCD是平行四边形
AB=10,AD=8,AC⊥BC,求BC、CD、
AC、OA的长及 ABCD的面积。
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究一
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下
图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
A
B
C
D
如图,在 ABCD中,
BC=10cm, AC=8cm, BD=14cm,
(1)△ BOC的周长是多少?
说明理由?
( 2) △ ABC与△ DBC的周长哪个长,
长多少?
A
B
D
C
O
若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
O
D
B
A
C
D
O
D
B
A
C
如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,
则CD=______.
5
如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
O
D
B
A
C
●
1<AD<9
公园有一片绿地,它的形状是平行四边形
绿地上要修几条笔直的小路,如图,AB=15cm
AD=12cm,AC⊥BC,求小路 BC,CD,OC的长
并算出绿地的面积.
课堂作业:
课本91页练习第3题,第6题。
家庭作业:
大册子39-40页《平行四边形性质(2)》
