一次函数复习学案
图片预览

文档简介
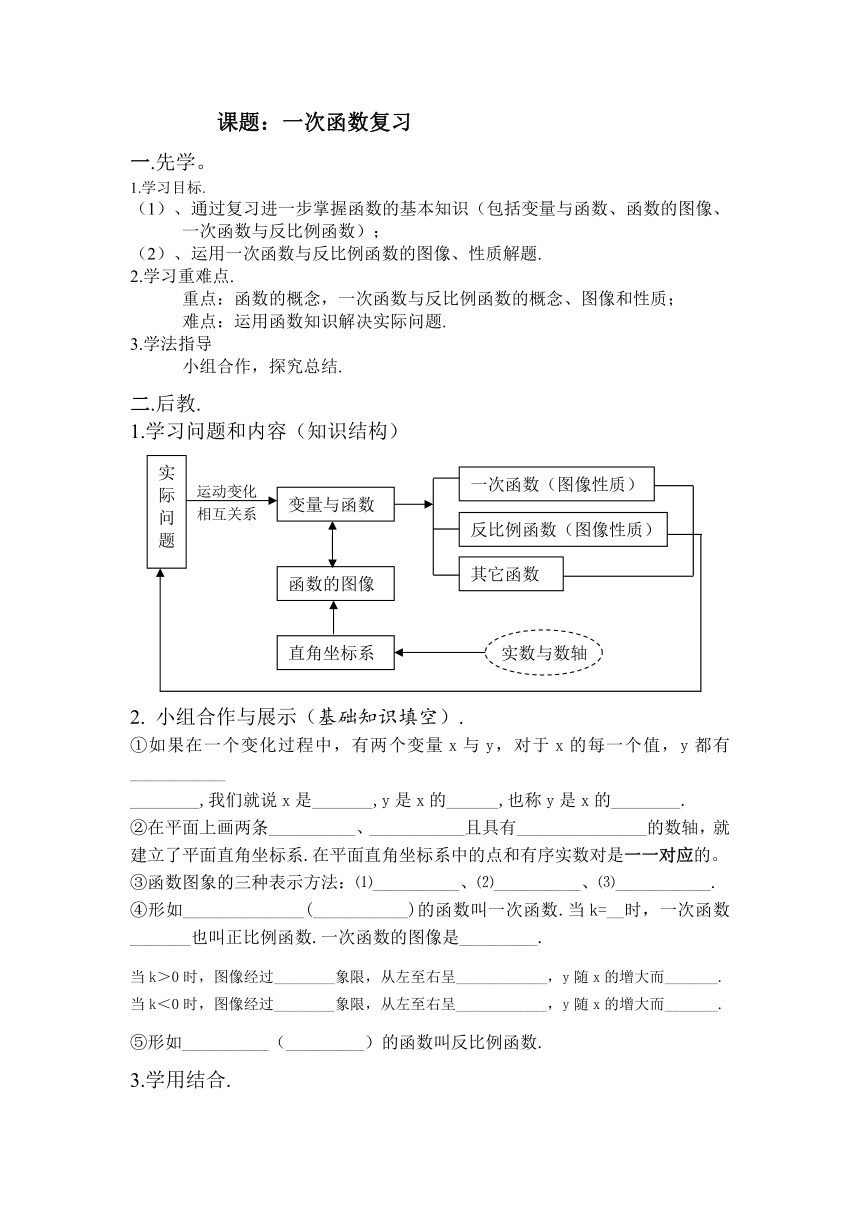
课题:一次函数复习
一.先学。
1.学习目标.
(1)、通过复习进一步掌握函数的基本知识(包括变量与函数、函数的图像、一次函数与反比例函数);
(2)、运用一次函数与反比例函数的图像、性质解题.
2.学习重难点.
重点:函数的概念,一次函数与反比例函数的概念、图像和性质;
难点:运用函数知识解决实际问题.
3.学法指导
小组合作,探究总结.
二.后教.
1.学习问题和内容(知识结构)
2. 小组合作与展示(基础知识填空).
①如果在一个变化过程中,有两个变量x与y,对于x的每一个值,y都有___________
________,我们就说x是_______,y是x的______,也称y是x的________.
②在平面上画两条__________、___________且具有_______________的数轴,就建立了平面直角坐标系.在平面直角坐标系中的点和有序实数对是一一对应的。
③函数图象的三种表示方法:⑴__________、⑵__________、⑶___________.
④形如______________(___________)的函数叫一次函数.当k=__时,一次函数_______也叫正比例函数.一次函数的图像是_________.
当k>0时,图像经过________象限,从左至右呈____________,y随x的增大而_______.
当k<0时,图像经过________象限,从左至右呈____________,y随x的增大而_______.
⑤形如__________(_________)的函数叫反比例函数.
3.学用结合.
1、若点P(2m-1,3)在第二象限,则m的取值范围是( )
A、 B、 C、 D、
2、直线y=-2x+3向下平移5个单位得到直线____________的图像。
3、已知函数,当x=________时,函数值为零.
4、如果点A(-3,a)与点B(3,4)关于y轴对称,那么a的值为______.
5、一次函数y=kx+b(k≠0)的图像经过点(3,3)和(1,-1),求它的函数关系式.
三.当堂练习.
专题一:一次函数与反比例函数的判定.
1、下列y与x的函数中,不是反比例函数的是( ).
A、 B、 C、 D、
2、若函数为一次函数,则m的值为____,若为正比例函数,则m的值为 ______.
专题二:k、b取值与一次函数图象位置.
3、如果一次函数y=kx+b的图像经过第一象限,且与y轴负半轴相交,那么( )
A、k>0,b>0 B、k>0,b<0
C、k<0,b>0 D、k<0,b<0
4、已知一次函数的图像经过第一、二、四象限,求m的取值范围.
专题三:数形结合思想.
5、如图是某出租车单程收费y /元与行程x/km
之间的函数关系图象,根据图像回答下列问题:
①当行驶8km时,收费应为___元;
②起步价为___元,超过___km时, 收费y /元
与行程x/km是一次函数关系;
③求出收费y /元与行程x/km之间的函数关系式.
四.作业布置.
1、某厂今年前五个月生产某种产品的月产量Q(件)与实践t(月)的函数图象如图所示,则对这种产品来说,下列说法正确的是( ).
A、1至3月每月产量逐月增加,4、5两月每月产量逐月减少
B、1至3月每月产量逐月增加,4、5两月每月产量与3月持平
C、1至3月每月产量逐月增加,4、5两月停止生产
D、1至3月每月产量不变,4、5两月停止生产
2、正方形ABCD的边长为4,P为DC上一点.设DP=x,求△APD的面积y关于x之间的函数关系式,并画出这个函数的图像.
五.课后反思与总结.
__________________________________________________________________________________________________
运动变化
相互关系
实际问题
实数与数轴
变量与函数
函数的图像
直角坐标系
反比例函数(图像性质)
其它函数
一次函数(图像性质)
O 3 8 x/km
y/元
11
5
P
A
C
B
D
x
O
1 2 3 4 5 t(月)
Q(件)
一.先学。
1.学习目标.
(1)、通过复习进一步掌握函数的基本知识(包括变量与函数、函数的图像、一次函数与反比例函数);
(2)、运用一次函数与反比例函数的图像、性质解题.
2.学习重难点.
重点:函数的概念,一次函数与反比例函数的概念、图像和性质;
难点:运用函数知识解决实际问题.
3.学法指导
小组合作,探究总结.
二.后教.
1.学习问题和内容(知识结构)
2. 小组合作与展示(基础知识填空).
①如果在一个变化过程中,有两个变量x与y,对于x的每一个值,y都有___________
________,我们就说x是_______,y是x的______,也称y是x的________.
②在平面上画两条__________、___________且具有_______________的数轴,就建立了平面直角坐标系.在平面直角坐标系中的点和有序实数对是一一对应的。
③函数图象的三种表示方法:⑴__________、⑵__________、⑶___________.
④形如______________(___________)的函数叫一次函数.当k=__时,一次函数_______也叫正比例函数.一次函数的图像是_________.
当k>0时,图像经过________象限,从左至右呈____________,y随x的增大而_______.
当k<0时,图像经过________象限,从左至右呈____________,y随x的增大而_______.
⑤形如__________(_________)的函数叫反比例函数.
3.学用结合.
1、若点P(2m-1,3)在第二象限,则m的取值范围是( )
A、 B、 C、 D、
2、直线y=-2x+3向下平移5个单位得到直线____________的图像。
3、已知函数,当x=________时,函数值为零.
4、如果点A(-3,a)与点B(3,4)关于y轴对称,那么a的值为______.
5、一次函数y=kx+b(k≠0)的图像经过点(3,3)和(1,-1),求它的函数关系式.
三.当堂练习.
专题一:一次函数与反比例函数的判定.
1、下列y与x的函数中,不是反比例函数的是( ).
A、 B、 C、 D、
2、若函数为一次函数,则m的值为____,若为正比例函数,则m的值为 ______.
专题二:k、b取值与一次函数图象位置.
3、如果一次函数y=kx+b的图像经过第一象限,且与y轴负半轴相交,那么( )
A、k>0,b>0 B、k>0,b<0
C、k<0,b>0 D、k<0,b<0
4、已知一次函数的图像经过第一、二、四象限,求m的取值范围.
专题三:数形结合思想.
5、如图是某出租车单程收费y /元与行程x/km
之间的函数关系图象,根据图像回答下列问题:
①当行驶8km时,收费应为___元;
②起步价为___元,超过___km时, 收费y /元
与行程x/km是一次函数关系;
③求出收费y /元与行程x/km之间的函数关系式.
四.作业布置.
1、某厂今年前五个月生产某种产品的月产量Q(件)与实践t(月)的函数图象如图所示,则对这种产品来说,下列说法正确的是( ).
A、1至3月每月产量逐月增加,4、5两月每月产量逐月减少
B、1至3月每月产量逐月增加,4、5两月每月产量与3月持平
C、1至3月每月产量逐月增加,4、5两月停止生产
D、1至3月每月产量不变,4、5两月停止生产
2、正方形ABCD的边长为4,P为DC上一点.设DP=x,求△APD的面积y关于x之间的函数关系式,并画出这个函数的图像.
五.课后反思与总结.
__________________________________________________________________________________________________
运动变化
相互关系
实际问题
实数与数轴
变量与函数
函数的图像
直角坐标系
反比例函数(图像性质)
其它函数
一次函数(图像性质)
O 3 8 x/km
y/元
11
5
P
A
C
B
D
x
O
1 2 3 4 5 t(月)
Q(件)
