云南省昭通市水富县云天化集团附属高中2022届高三上学期7月摸底测试数学(文)试题 Word版含解析
文档属性
| 名称 | 云南省昭通市水富县云天化集团附属高中2022届高三上学期7月摸底测试数学(文)试题 Word版含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 15:02:19 | ||
图片预览




文档简介
云天化集团附属高中2022届高三上学期7月摸底测试
数学(文科)试卷
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(客观题)两部分,共4页。考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试卷上答题无效,试卷满分150分,考试时间120分钟。
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚,并请认真填涂准考证号。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后,再选涂其他答案标号。答在试卷上的答案无效。
第I卷(选择题,共分)
一、选择题:(本大题共小题,每小题分)
1.若复数满足,则复数在复平面内对应的点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知集合,,则(
).
A.
B.
C.
D.
3.正项等比数列中,,,则的值是(
)
A.
B.
C.
D.
4.“中国剩余定理”又称“孙子定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2020这2020个数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列{an},则此数列的项数为(
)
A.167
B.168
C.169
D.170
5.“”是“”的(
)
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
6.正三棱柱中,,,该三棱柱的外接球的体积为(
)
A.
B.
C.
D.
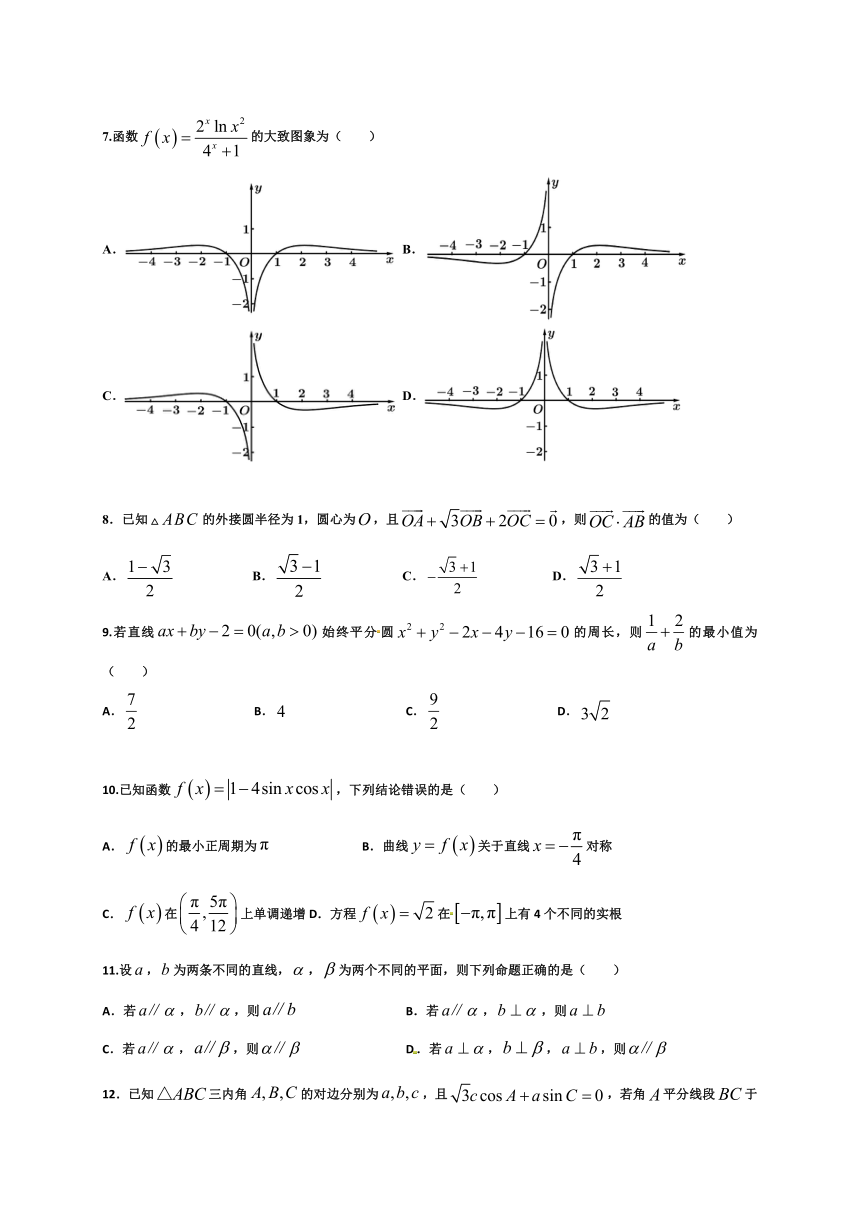
7.函数的大致图象为(
)
A.
B.
C.
D.
8.已知的外接圆半径为1,圆心为,且,则的值为(
)
A.
B.
C.
D.
9.若直线始终平分圆的周长,则的最小值为(
)
A.
B.
C.
D.
10.已知函数,下列结论错误的是(
)
A.的最小正周期为
B.曲线关于直线对称
C.在上单调递增D.方程在上有4个不同的实根
11.设,为两条不同的直线,,为两个不同的平面,则下列命题正确的是(
)
A.若,,则
B.若,,则
C.若,,则
D.若,,,则
12.已知三内角的对边分别为,且,若角平分线段于点,且,则的最小值为(
)
A.
B.
C.
D.
第Ⅱ卷
客观题(共分)
二、填空题:(每小题5分,共20分)
13.若的展开式中的常数项是_________.
14.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化阴阳术数之源.河图的排列结构如图所示,一与六共宗居下,二与七为朋居上,三与八同道居左,四与九为友居右,五与十相守居中,其中白圈为阳数,黑点为阴数,若从阳数和阴数中各取一数,则其差的绝对值为的概率为_________.
15.设满足约束条件,则目标函数的最大值是__________.
16.已知椭圆的左、右焦点分别为,,为第二象限内椭圆上的一点,连接交轴于点,若,,其中为坐标原点,则该椭圆的离心率为______.
三、解答题:(本大题共小题,共分,其中22题10分,其余每题12分。解答应写出文字说明,证明过程或演算步骤。)
17.(本小题满分12分)
已知等差数列的公差,且,,,成等比数列,若数列满足:
.
(1)求数列的通项公式;
(2)求数列的前项和.
18.(本小题满分12分)
某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出、两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于时为废品,指标值在为一等品,大于为特等品.现把测量数据整理如下,其中配方废品有件
配方的频数分布表
质量指标值分组
频数
(1)求,的值;
(2)试确定配方和配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
19.(本小题满分12分)
如图,三棱锥,均为底面边长为、侧棱长为的正棱锥,且四边形是边长为的菱形(点在平面的同侧),交于点.
(1)证明:平面平面;
(2)求点到平面的距离.
(本小题满分12分)
已知抛物线的焦点为,过点且垂直于轴的直线与交于两点,(点为坐标原点)的面积为2.
(1)求抛物线的方程;
(2)若过点的两直线,的倾斜角互补,直线与抛物线交于两点,直线与抛物线交于两点,与的面积相等,求实数的取值范围.
21.(本小题满分12分)
已知函数.
(1)当时,试判断函数的单调性;
(2)若,且当时,恒成立.有且只有一个实数解,证明:.
22.(本小题满分10分)
在平面直角坐标系中,为曲线(为参数)上的动点,将点纵坐标变为原来的倍,横坐标变为原来的一半得到点,记点的轨迹为,以坐标原点为极点,轴非负半轴为极轴建立极坐标系.
求曲线的极坐标方程;
(2),是曲线上不同于的两点,且,,求的取值范围.
云天化集团附属高中2022届高三上学期7月摸底测试
数学(文科)答案
选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
D
C
A
C
B
A
D
A
C
C
B
D
1.【答案】D
【解析】,∴复数在复平面内对应的点(2,-1)在第四象限,故选D
2.【答案】C
【解析】∵,,
∴或,∴.故选C.
3.【答案】A
【解析】设正项等比数列的公比为,,,
∴,,解得,
则.
4.【答案】C
【解析】由题意得,能被3除余1且被4除余1的数就是能被12除余1的数,所以,,由,即,所以,由,所以此数列的项数为169.
故选C
5.【答案】B
【解析】,,若,则,[]
所以“”是“”的必要不充分条件.
6.【答案】A
【解析】函数的定义域为,且,,所以,函数为偶函数,排除BC选项;
当时,,则,排除D选项.故选A.
7.答案】D
【解析】外接球的球心在上下底面重心的连接线段的中点上,底面重心到棱柱顶点的距离为,球心距底面的重心的距离为,外接球的半径,
所以该三棱柱的体积.
8.【答案】A
【解析】由题设,两边平方可得,所以,,构成直角三角形.,夹角,,夹角,.故选A
9.【答案】C
【解析】∵直线始终平分圆的周长,
∴直线过圆心,
∴,即,
∵,
∴
10.【答案】C
【解析】,
作出在上的图象(先作出的图象,
再利用平移变换和翻折变换得到的图象),如图所示,
由图可知A、B、D正确,C错误.
11.【答案】B
【解析】由,为两条不同的直线,,为两个不同的平面,
在A中,若,,则与相交、平行或异面,故A错误;
在B中,若,,则,故B正确;
在C中,若,,则与相交或平行,故C错误;
在D中,若,,,则由面面垂直的判定定理得,故D错误.
12.【答案】D
【解析】由及正弦定理,得,
因,,所以,即,[]
又,所以.如图,
,
所以,
所以,即,
∴,当且仅当,,即时,等号成立,所以的最小值为.故选D.
填空题:
13.【答案】
【解析】的展开式中的常数项是
14.【答案】
【解析】∵阳数为;阴数为,
∴从阳数和阴数中各取一数的所有组合共有个,
满足差的绝对值为的有,,,,共个,
则,
15.【答案】3
【解析】画出可行域如下图阴影部分所示,目标函数,表示可行域内的点和点连线的斜率,由图可知,其最大值为.
【答案】
【解析】因为,所以,由题意可得,则,
因为,所以,所以.因为,所以,,所以,可得,解得.
解答题:
【答案】(1);(2).
【解析】(1)因为,所以由等差数列的性质得,即,
因为成等比数列,所以,
即,
又,,所以,,
所以.
(2)因为,
所以当时,,所以
当时,由,
得,
所以,
所以,
,
所以
,
所以.
18.【答案】(1),;(2)配方好些,详见解析.
【解析】(1)依题意,配方样本容量相同,设为,
又配方废品有件,由配方的频频率分布直方图,
得废品的频率为,解得,
∴.
由,解得,
因此,的值分别为,.
(2)由(1)及配方的频数分布表得,
配方质量指标值的样本平均数为
,
质量指标值的样本方差为:
;[来源:学
科
网]
由配方的频频率分布直方图得,
配方质量指标值的样本平均数为:
,
质量指标值的样本方差为:
,
综上,,
即两种配方质量指标值的样本平均数相等,但配方质量指标值不够稳定,
所以选择配方比较好.
19.【解析】(1)如图所示,连接PO,OQ,PQ,
因为,O为BD的中点,所以,
同理可得,
又由,PO,平面POQ,
所以平面POQ.
又因为平面ABCD,所以平面平面ABCD.(5分)
(2)如图所示,分别过P,Q作平面ABCD的垂线,垂足分别为,,
则,在AC上,且,分别为AO,OC的三等分点,
且,,,所以四边形为矩形,
所以,且,
所以,
取BC的中点E,则,
又由(1)得平面平面ABCD,
而平面平面,,所以平面PQC,
设点P到平面QBC的距离为,
则由,可得,
即,即,
解得,点到平面的距离为.(12分)
20.【解析】(1)因为焦点,所以点的坐标分别为,.
所以,故.
故抛物线的方程为.(4分)
(2)由题意可知直线的斜率存在,且不为0,设直线.
点,.
联立方程可得,消去,可得.
则.
因为,
所以,
焦点到直线的距离,
所以.
设直线,与抛物线方程联立可得,
将用替换,可得
由可得,
即,两边平方并化简可得,
所以,解得.
又由且得或,可知,
所以,即,所以,
所以实数的取值范围是.(12分)
21.【解析】的定义域为
(1)当时,,
则,,
所以当时,,此时函数单调递增;
当时,,此时函数单调递减.
综上,函数在区间上单调递增,在区间上单调递减.
(5分)
(2)由题意可得,,令,
解得.
因为,所以,,
所以在上有唯一零点.
当时,在上单调递增;
当时,,在上单调递减.
所以.
因为在上恒成立,且有且只有一个实数解,
所以即
消去并整理得.
令,则,,
在上恒成立,所以在上单调递增,
又,,所以.
又,且函数在上单调递增,所以.(12分)
22.解析】曲线(为参数),
化为普通方程为:,
所以曲线的极坐标方程为.(5分)
设,,,
因为,所以,
所以的取值范围是(10分)
数学(文科)试卷
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(客观题)两部分,共4页。考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试卷上答题无效,试卷满分150分,考试时间120分钟。
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚,并请认真填涂准考证号。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后,再选涂其他答案标号。答在试卷上的答案无效。
第I卷(选择题,共分)
一、选择题:(本大题共小题,每小题分)
1.若复数满足,则复数在复平面内对应的点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知集合,,则(
).
A.
B.
C.
D.
3.正项等比数列中,,,则的值是(
)
A.
B.
C.
D.
4.“中国剩余定理”又称“孙子定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2020这2020个数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列{an},则此数列的项数为(
)
A.167
B.168
C.169
D.170
5.“”是“”的(
)
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
6.正三棱柱中,,,该三棱柱的外接球的体积为(
)
A.
B.
C.
D.
7.函数的大致图象为(
)
A.
B.
C.
D.
8.已知的外接圆半径为1,圆心为,且,则的值为(
)
A.
B.
C.
D.
9.若直线始终平分圆的周长,则的最小值为(
)
A.
B.
C.
D.
10.已知函数,下列结论错误的是(
)
A.的最小正周期为
B.曲线关于直线对称
C.在上单调递增D.方程在上有4个不同的实根
11.设,为两条不同的直线,,为两个不同的平面,则下列命题正确的是(
)
A.若,,则
B.若,,则
C.若,,则
D.若,,,则
12.已知三内角的对边分别为,且,若角平分线段于点,且,则的最小值为(
)
A.
B.
C.
D.
第Ⅱ卷
客观题(共分)
二、填空题:(每小题5分,共20分)
13.若的展开式中的常数项是_________.
14.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化阴阳术数之源.河图的排列结构如图所示,一与六共宗居下,二与七为朋居上,三与八同道居左,四与九为友居右,五与十相守居中,其中白圈为阳数,黑点为阴数,若从阳数和阴数中各取一数,则其差的绝对值为的概率为_________.
15.设满足约束条件,则目标函数的最大值是__________.
16.已知椭圆的左、右焦点分别为,,为第二象限内椭圆上的一点,连接交轴于点,若,,其中为坐标原点,则该椭圆的离心率为______.
三、解答题:(本大题共小题,共分,其中22题10分,其余每题12分。解答应写出文字说明,证明过程或演算步骤。)
17.(本小题满分12分)
已知等差数列的公差,且,,,成等比数列,若数列满足:
.
(1)求数列的通项公式;
(2)求数列的前项和.
18.(本小题满分12分)
某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出、两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于时为废品,指标值在为一等品,大于为特等品.现把测量数据整理如下,其中配方废品有件
配方的频数分布表
质量指标值分组
频数
(1)求,的值;
(2)试确定配方和配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
19.(本小题满分12分)
如图,三棱锥,均为底面边长为、侧棱长为的正棱锥,且四边形是边长为的菱形(点在平面的同侧),交于点.
(1)证明:平面平面;
(2)求点到平面的距离.
(本小题满分12分)
已知抛物线的焦点为,过点且垂直于轴的直线与交于两点,(点为坐标原点)的面积为2.
(1)求抛物线的方程;
(2)若过点的两直线,的倾斜角互补,直线与抛物线交于两点,直线与抛物线交于两点,与的面积相等,求实数的取值范围.
21.(本小题满分12分)
已知函数.
(1)当时,试判断函数的单调性;
(2)若,且当时,恒成立.有且只有一个实数解,证明:.
22.(本小题满分10分)
在平面直角坐标系中,为曲线(为参数)上的动点,将点纵坐标变为原来的倍,横坐标变为原来的一半得到点,记点的轨迹为,以坐标原点为极点,轴非负半轴为极轴建立极坐标系.
求曲线的极坐标方程;
(2),是曲线上不同于的两点,且,,求的取值范围.
云天化集团附属高中2022届高三上学期7月摸底测试
数学(文科)答案
选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
D
C
A
C
B
A
D
A
C
C
B
D
1.【答案】D
【解析】,∴复数在复平面内对应的点(2,-1)在第四象限,故选D
2.【答案】C
【解析】∵,,
∴或,∴.故选C.
3.【答案】A
【解析】设正项等比数列的公比为,,,
∴,,解得,
则.
4.【答案】C
【解析】由题意得,能被3除余1且被4除余1的数就是能被12除余1的数,所以,,由,即,所以,由,所以此数列的项数为169.
故选C
5.【答案】B
【解析】,,若,则,[]
所以“”是“”的必要不充分条件.
6.【答案】A
【解析】函数的定义域为,且,,所以,函数为偶函数,排除BC选项;
当时,,则,排除D选项.故选A.
7.答案】D
【解析】外接球的球心在上下底面重心的连接线段的中点上,底面重心到棱柱顶点的距离为,球心距底面的重心的距离为,外接球的半径,
所以该三棱柱的体积.
8.【答案】A
【解析】由题设,两边平方可得,所以,,构成直角三角形.,夹角,,夹角,.故选A
9.【答案】C
【解析】∵直线始终平分圆的周长,
∴直线过圆心,
∴,即,
∵,
∴
10.【答案】C
【解析】,
作出在上的图象(先作出的图象,
再利用平移变换和翻折变换得到的图象),如图所示,
由图可知A、B、D正确,C错误.
11.【答案】B
【解析】由,为两条不同的直线,,为两个不同的平面,
在A中,若,,则与相交、平行或异面,故A错误;
在B中,若,,则,故B正确;
在C中,若,,则与相交或平行,故C错误;
在D中,若,,,则由面面垂直的判定定理得,故D错误.
12.【答案】D
【解析】由及正弦定理,得,
因,,所以,即,[]
又,所以.如图,
,
所以,
所以,即,
∴,当且仅当,,即时,等号成立,所以的最小值为.故选D.
填空题:
13.【答案】
【解析】的展开式中的常数项是
14.【答案】
【解析】∵阳数为;阴数为,
∴从阳数和阴数中各取一数的所有组合共有个,
满足差的绝对值为的有,,,,共个,
则,
15.【答案】3
【解析】画出可行域如下图阴影部分所示,目标函数,表示可行域内的点和点连线的斜率,由图可知,其最大值为.
【答案】
【解析】因为,所以,由题意可得,则,
因为,所以,所以.因为,所以,,所以,可得,解得.
解答题:
【答案】(1);(2).
【解析】(1)因为,所以由等差数列的性质得,即,
因为成等比数列,所以,
即,
又,,所以,,
所以.
(2)因为,
所以当时,,所以
当时,由,
得,
所以,
所以,
,
所以
,
所以.
18.【答案】(1),;(2)配方好些,详见解析.
【解析】(1)依题意,配方样本容量相同,设为,
又配方废品有件,由配方的频频率分布直方图,
得废品的频率为,解得,
∴.
由,解得,
因此,的值分别为,.
(2)由(1)及配方的频数分布表得,
配方质量指标值的样本平均数为
,
质量指标值的样本方差为:
;[来源:学
科
网]
由配方的频频率分布直方图得,
配方质量指标值的样本平均数为:
,
质量指标值的样本方差为:
,
综上,,
即两种配方质量指标值的样本平均数相等,但配方质量指标值不够稳定,
所以选择配方比较好.
19.【解析】(1)如图所示,连接PO,OQ,PQ,
因为,O为BD的中点,所以,
同理可得,
又由,PO,平面POQ,
所以平面POQ.
又因为平面ABCD,所以平面平面ABCD.(5分)
(2)如图所示,分别过P,Q作平面ABCD的垂线,垂足分别为,,
则,在AC上,且,分别为AO,OC的三等分点,
且,,,所以四边形为矩形,
所以,且,
所以,
取BC的中点E,则,
又由(1)得平面平面ABCD,
而平面平面,,所以平面PQC,
设点P到平面QBC的距离为,
则由,可得,
即,即,
解得,点到平面的距离为.(12分)
20.【解析】(1)因为焦点,所以点的坐标分别为,.
所以,故.
故抛物线的方程为.(4分)
(2)由题意可知直线的斜率存在,且不为0,设直线.
点,.
联立方程可得,消去,可得.
则.
因为,
所以,
焦点到直线的距离,
所以.
设直线,与抛物线方程联立可得,
将用替换,可得
由可得,
即,两边平方并化简可得,
所以,解得.
又由且得或,可知,
所以,即,所以,
所以实数的取值范围是.(12分)
21.【解析】的定义域为
(1)当时,,
则,,
所以当时,,此时函数单调递增;
当时,,此时函数单调递减.
综上,函数在区间上单调递增,在区间上单调递减.
(5分)
(2)由题意可得,,令,
解得.
因为,所以,,
所以在上有唯一零点.
当时,在上单调递增;
当时,,在上单调递减.
所以.
因为在上恒成立,且有且只有一个实数解,
所以即
消去并整理得.
令,则,,
在上恒成立,所以在上单调递增,
又,,所以.
又,且函数在上单调递增,所以.(12分)
22.解析】曲线(为参数),
化为普通方程为:,
所以曲线的极坐标方程为.(5分)
设,,,
因为,所以,
所以的取值范围是(10分)
同课章节目录
