五年级下册数学教案-3.10 公倍数和最小公倍数 苏教版
文档属性
| 名称 | 五年级下册数学教案-3.10 公倍数和最小公倍数 苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 66.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 19:22:36 | ||
图片预览



文档简介
《公倍数和最小公倍数》教学设计
【教学目标】
1.使学生通过具体的操作和交流活动,理解公倍数与最小公倍数的含义,会用列举的方法求10以内两个数的最小公倍数。
2.使学生经历探索和发现数学知识的过程,积累数学活动的经验,进一步培养自主探索与合作交流的能力,感受解决问题策略的多样性,发展数学思考。
3.使学生在参与学习活动的过程中,培养主动与他人合作交流的意识,体验学习和探索活动的乐趣,增强学生参与探索学习的主动性和积极性,提升学生的数学素养。
【教学重难点】
教学重点:理解公倍数含义,会求10以内两个数的最小公倍数。
教学难点:理解公倍数含义,引导学生经历概念的形成过程。
【教学过程】
一、创设情境,提供素材
(多媒体出示教材P22页例1)用长3厘米、宽2厘米的长方形纸片分别铺下面的正方形。
?
?
谈话:仔细观察,你发现了哪些数学信息?
请同学们猜想一下,可以正好铺满哪个正方形?你是怎样想的?
预设猜想的理由:1.大面积除以小面积
2.正方形边长与小长方形长和宽的关系
【设计意图】猜想是对事物变化方向的一种“试探”性判断,通过让学生大胆猜想,使学习目标以问题的形式提出,激发了学生的思维,使学生主动在头脑中搜索相关知识。让学生简单陈述猜想的根据,有利于培养学生有根据的猜想的良好习惯。
二、分析素材,理解概念
1.操作验证,同桌交流
谈话:每个同学手中都有一叠长3厘米、宽2厘米的长方形贴纸和两个边长分别为6厘米和8厘米的正方形,请同学们先自己摆一摆,看能正好铺满哪个正方形。
学生活动,教师巡视指导,了解信息。(摆完的和同桌交流你是怎样摆的)
2.全班交流,初步感知
(1)交流边长6厘米的正方形摆的过程。
多媒体展示学生的摆法,学生结合直观图讲解摆法。
教师结合学生交流适时质疑:用长边摆了两次,为什么?
用宽边摆了3次,为什么?
(2)分析正方形边长与长方形长和宽的关系。
谈话:根据刚才摆的过程,你能利用这些数据,用算式表示为什么这样摆吗?
学生独立思考,在小组内交流。教师巡视指导。
预设:算式6÷2=3;6÷3=2
同桌互相说一说算式表示的意义,教师重点引导学生将摆的过程引导到思考数据之间的关系上。
小结“为什么边长是6厘米的正方形能铺满?”
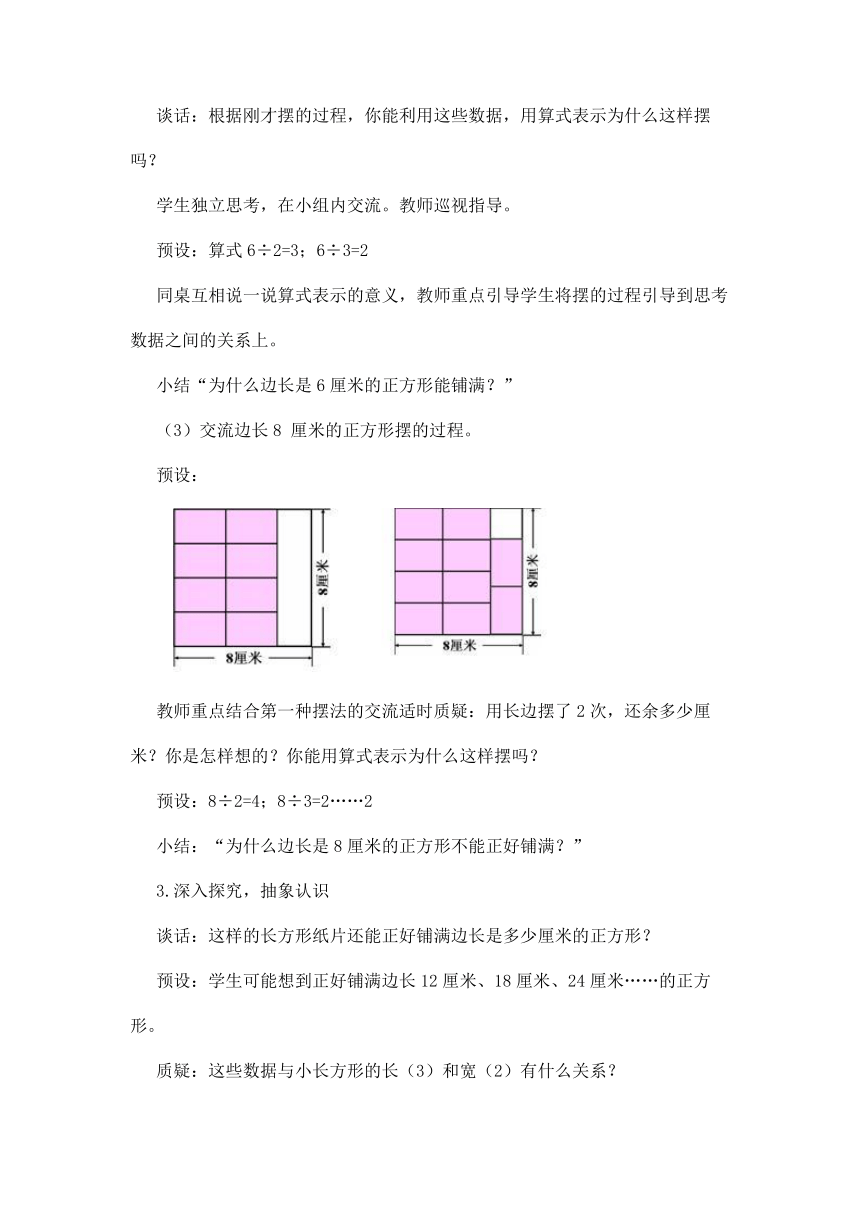
(3)交流边长8 厘米的正方形摆的过程。
预设:
?
教师重点结合第一种摆法的交流适时质疑:用长边摆了2次,还余多少厘米?你是怎样想的?你能用算式表示为什么这样摆吗?
预设:8÷2=4;8÷3=2……2
小结:“为什么边长是8厘米的正方形不能正好铺满?”
3.深入探究,抽象认识
谈话:这样的长方形纸片还能正好铺满边长是多少厘米的正方形?
预设:学生可能想到正好铺满边长12厘米、18厘米、24厘米……的正方形。
质疑:这些数据与小长方形的长(3)和宽(2)有什么关系?
师重点引导学生理解边长的厘米数既是2的倍数,又是3的倍数。
【设计意图】摆一摆、贴一贴,给学生提供了直观的实物模型,让学生在实践操作活动后展开思考与分析,经历概念的发生与形成过程,由直观到抽象逐步完成“公倍数”这一概念建模。
三、借助素材,总结概念
师引导学生给“6、12、18、24……”这样的数起名字。
师总结并板书:6、12、18、24……既是2的倍数,又是3的倍数,它们是2和3的公倍数。(板书课题:公倍数)
质疑:为什么用“公倍数”这个名字?
重点引导学生理解“公有”、“既是…又是”的概念内涵。
追问:8是2和3的公倍数吗?为什么?
你能再说出几个2和3的公倍数吗?能说完吗?为什么?
小结:因为一个数的倍数的个数是无限的,所以两个数的公倍数的个数也是无限的,所以说不完。
【设计意图】通过让学生给“公倍数”起名加深对这一概念内涵的理解,突出对“公有”理解;通过反例进一步凸显公倍数的含义,加深学生对“公倍数”这一概念外延的识别。
四、应用概念,深化理解
1.独立探究,小组交流
谈话:(多媒体出示例2)6和9的公倍数有哪些?请你试着找一找,写在练习纸上,并在小组内交流。
学生活动,师巡视指导,了解信息。
2.全班交流
预设:法一:先分别找6和9的倍数,再找6和9的公倍数。
法二:先找6的倍数,再从6的倍数中找9的倍数。
法三:先找9的倍数,再从9的倍数中找6的倍数。
法四:先找出6和9的最小公倍数18,6和9的公倍数就是18的倍数。
师注意引导法二、三中法三更简捷,重点交流法三,并让学生明确所有方法均为列举法。如果法四不出现可不提。
教师引导学生观察公倍数:你发现了什么?顺势揭示最小公倍数的概念。(板书课题:最小公倍数)进一步体会公倍数有无数个的特征。
追问:2和3的最小公倍数是几?
3.用集合图表示公倍数、倍数
谈话:以前我们学过用集合圈分别表示6和9的倍数。(多媒体出示)十九世纪英国著名数学家韦恩想了个好办法:把两个集合圈合起来,这个图就叫韦恩图。(多媒体动态演示)
师引导学生分析韦恩图的各部分表示的意义。通过重点质疑加深对公倍数意义的理解:中间部分的数表示什么?“12”为什么不能填在中间的圈中?
小结:同学们这么勤于思考,老师相信你们一定会像韦恩一样有更多的创造和发现。
【设计意图】学生通过独立探索,交流、比较,掌握用列举法求公倍数和最小公倍数的方法,并适时揭示出最小公倍数的意义。通过韦恩图的介绍激发学生的再创造的动机,会分析并填写韦恩图,进而加深学生对公倍数意义的理解。
五、巩固练习,拓展延伸
(多媒体出示练习题)
1.把50以内6和8的倍数、公倍数分别填在下面的圈里,再找出它们的最小公倍数。
6的倍数 8的倍数
?
?????????? ?6的倍数 8的倍数
?
?
?
?????????????? 6和8的公倍数
6和8的最小公倍数:
交流时注意让学生自己发现错误、找到出错原因并改正,培养学生仔细读题的良好习惯。
2.红棋每次走3格,黄棋每次走4格,你能在两种棋都走的方格里涂上颜色吗?
?
交流时让学生说明求什么?怎样找最快?
3.走进生活。《阿凡提的故事》(机动练习)
从前有个长工,在巴依老爷家干了一年也没有拿到一个铜板。长工们于是自发地组织了起来并邀请阿凡提帮他们去向巴依老爷讨工资。巴依老爷含着烟斗冷笑着说:“工资我可以给你,不过我的钱都在我的账房先生那里。从八月一日起,我要连续出去收账3天才休息一天,我的账房先生要连续收账5天才可以休息一天,你们就在我们两人同时休息的时候来吧。我肯定给钱。”阿凡提动了动脑筋,便带长工们离开了。到了某天,他真的从巴依老爷家帮长工拿到了工钱。
??? 请大家想一想,阿凡提是哪天去巴依老爷家的?他用的是什么办法找到这个日期的?你准备如何解决这个问题?
【设计意图】练习题,从抽象的数学知识到学生喜欢的童话世界生活,让学生体会数学与生活的密切联系,使学生的应用中进一步加深对概念的理解。
五、反思总结,梳理提升
教师将引导学生从以下几个方面梳理总结:
1.公倍数、最小公倍数的含义
2.列举法求公倍数、最小公倍数
3.用韦恩图表示倍数、公倍数
4.用不同的方法解决统一问题
……
?
板书设计:
公倍数和最小公倍数
6÷2=3 8÷2=4
6÷3=2 8÷3=2……2
6、12、18、24……既是2的倍数,又是3的倍数,
它们是2和3的公倍数。
【教学目标】
1.使学生通过具体的操作和交流活动,理解公倍数与最小公倍数的含义,会用列举的方法求10以内两个数的最小公倍数。
2.使学生经历探索和发现数学知识的过程,积累数学活动的经验,进一步培养自主探索与合作交流的能力,感受解决问题策略的多样性,发展数学思考。
3.使学生在参与学习活动的过程中,培养主动与他人合作交流的意识,体验学习和探索活动的乐趣,增强学生参与探索学习的主动性和积极性,提升学生的数学素养。
【教学重难点】
教学重点:理解公倍数含义,会求10以内两个数的最小公倍数。
教学难点:理解公倍数含义,引导学生经历概念的形成过程。
【教学过程】
一、创设情境,提供素材
(多媒体出示教材P22页例1)用长3厘米、宽2厘米的长方形纸片分别铺下面的正方形。
?
?
谈话:仔细观察,你发现了哪些数学信息?
请同学们猜想一下,可以正好铺满哪个正方形?你是怎样想的?
预设猜想的理由:1.大面积除以小面积
2.正方形边长与小长方形长和宽的关系
【设计意图】猜想是对事物变化方向的一种“试探”性判断,通过让学生大胆猜想,使学习目标以问题的形式提出,激发了学生的思维,使学生主动在头脑中搜索相关知识。让学生简单陈述猜想的根据,有利于培养学生有根据的猜想的良好习惯。
二、分析素材,理解概念
1.操作验证,同桌交流
谈话:每个同学手中都有一叠长3厘米、宽2厘米的长方形贴纸和两个边长分别为6厘米和8厘米的正方形,请同学们先自己摆一摆,看能正好铺满哪个正方形。
学生活动,教师巡视指导,了解信息。(摆完的和同桌交流你是怎样摆的)
2.全班交流,初步感知
(1)交流边长6厘米的正方形摆的过程。
多媒体展示学生的摆法,学生结合直观图讲解摆法。
教师结合学生交流适时质疑:用长边摆了两次,为什么?
用宽边摆了3次,为什么?
(2)分析正方形边长与长方形长和宽的关系。
谈话:根据刚才摆的过程,你能利用这些数据,用算式表示为什么这样摆吗?
学生独立思考,在小组内交流。教师巡视指导。
预设:算式6÷2=3;6÷3=2
同桌互相说一说算式表示的意义,教师重点引导学生将摆的过程引导到思考数据之间的关系上。
小结“为什么边长是6厘米的正方形能铺满?”
(3)交流边长8 厘米的正方形摆的过程。
预设:
?
教师重点结合第一种摆法的交流适时质疑:用长边摆了2次,还余多少厘米?你是怎样想的?你能用算式表示为什么这样摆吗?
预设:8÷2=4;8÷3=2……2
小结:“为什么边长是8厘米的正方形不能正好铺满?”
3.深入探究,抽象认识
谈话:这样的长方形纸片还能正好铺满边长是多少厘米的正方形?
预设:学生可能想到正好铺满边长12厘米、18厘米、24厘米……的正方形。
质疑:这些数据与小长方形的长(3)和宽(2)有什么关系?
师重点引导学生理解边长的厘米数既是2的倍数,又是3的倍数。
【设计意图】摆一摆、贴一贴,给学生提供了直观的实物模型,让学生在实践操作活动后展开思考与分析,经历概念的发生与形成过程,由直观到抽象逐步完成“公倍数”这一概念建模。
三、借助素材,总结概念
师引导学生给“6、12、18、24……”这样的数起名字。
师总结并板书:6、12、18、24……既是2的倍数,又是3的倍数,它们是2和3的公倍数。(板书课题:公倍数)
质疑:为什么用“公倍数”这个名字?
重点引导学生理解“公有”、“既是…又是”的概念内涵。
追问:8是2和3的公倍数吗?为什么?
你能再说出几个2和3的公倍数吗?能说完吗?为什么?
小结:因为一个数的倍数的个数是无限的,所以两个数的公倍数的个数也是无限的,所以说不完。
【设计意图】通过让学生给“公倍数”起名加深对这一概念内涵的理解,突出对“公有”理解;通过反例进一步凸显公倍数的含义,加深学生对“公倍数”这一概念外延的识别。
四、应用概念,深化理解
1.独立探究,小组交流
谈话:(多媒体出示例2)6和9的公倍数有哪些?请你试着找一找,写在练习纸上,并在小组内交流。
学生活动,师巡视指导,了解信息。
2.全班交流
预设:法一:先分别找6和9的倍数,再找6和9的公倍数。
法二:先找6的倍数,再从6的倍数中找9的倍数。
法三:先找9的倍数,再从9的倍数中找6的倍数。
法四:先找出6和9的最小公倍数18,6和9的公倍数就是18的倍数。
师注意引导法二、三中法三更简捷,重点交流法三,并让学生明确所有方法均为列举法。如果法四不出现可不提。
教师引导学生观察公倍数:你发现了什么?顺势揭示最小公倍数的概念。(板书课题:最小公倍数)进一步体会公倍数有无数个的特征。
追问:2和3的最小公倍数是几?
3.用集合图表示公倍数、倍数
谈话:以前我们学过用集合圈分别表示6和9的倍数。(多媒体出示)十九世纪英国著名数学家韦恩想了个好办法:把两个集合圈合起来,这个图就叫韦恩图。(多媒体动态演示)
师引导学生分析韦恩图的各部分表示的意义。通过重点质疑加深对公倍数意义的理解:中间部分的数表示什么?“12”为什么不能填在中间的圈中?
小结:同学们这么勤于思考,老师相信你们一定会像韦恩一样有更多的创造和发现。
【设计意图】学生通过独立探索,交流、比较,掌握用列举法求公倍数和最小公倍数的方法,并适时揭示出最小公倍数的意义。通过韦恩图的介绍激发学生的再创造的动机,会分析并填写韦恩图,进而加深学生对公倍数意义的理解。
五、巩固练习,拓展延伸
(多媒体出示练习题)
1.把50以内6和8的倍数、公倍数分别填在下面的圈里,再找出它们的最小公倍数。
6的倍数 8的倍数
?
?????????? ?6的倍数 8的倍数
?
?
?
?????????????? 6和8的公倍数
6和8的最小公倍数:
交流时注意让学生自己发现错误、找到出错原因并改正,培养学生仔细读题的良好习惯。
2.红棋每次走3格,黄棋每次走4格,你能在两种棋都走的方格里涂上颜色吗?
?
交流时让学生说明求什么?怎样找最快?
3.走进生活。《阿凡提的故事》(机动练习)
从前有个长工,在巴依老爷家干了一年也没有拿到一个铜板。长工们于是自发地组织了起来并邀请阿凡提帮他们去向巴依老爷讨工资。巴依老爷含着烟斗冷笑着说:“工资我可以给你,不过我的钱都在我的账房先生那里。从八月一日起,我要连续出去收账3天才休息一天,我的账房先生要连续收账5天才可以休息一天,你们就在我们两人同时休息的时候来吧。我肯定给钱。”阿凡提动了动脑筋,便带长工们离开了。到了某天,他真的从巴依老爷家帮长工拿到了工钱。
??? 请大家想一想,阿凡提是哪天去巴依老爷家的?他用的是什么办法找到这个日期的?你准备如何解决这个问题?
【设计意图】练习题,从抽象的数学知识到学生喜欢的童话世界生活,让学生体会数学与生活的密切联系,使学生的应用中进一步加深对概念的理解。
五、反思总结,梳理提升
教师将引导学生从以下几个方面梳理总结:
1.公倍数、最小公倍数的含义
2.列举法求公倍数、最小公倍数
3.用韦恩图表示倍数、公倍数
4.用不同的方法解决统一问题
……
?
板书设计:
公倍数和最小公倍数
6÷2=3 8÷2=4
6÷3=2 8÷3=2……2
6、12、18、24……既是2的倍数,又是3的倍数,
它们是2和3的公倍数。
