2021-2022学年湘教新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 357.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:45:50 | ||
图片预览



文档简介
2021-2022学年湘教新版九年级上册数学《第1章
反比例函数》单元测试卷
一.选择题
1.下列函数中,y是x的反比例函数的是( )
A.y=
B.y=
C.y=3x
D.y=x2
2.若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2,3),则另一个交点的坐标是( )
A.(2,3)
B.(3,2)
C.(﹣2,3)
D.(﹣2,﹣3)
3.若双曲线位于第二、四象限,则k的取值范围是( )
A.k<1
B.k≥1
C.k>1
D.k≠1
4.已知反比例函数的图象经过点P(1,2),则这个函数的图象位于( )
A.第二、三象限
B.第一、三象限
C.第二、四象限
D.第三、四象限
5.已知y是x的反比例函数,并且当x=2时,y=6,则y关于x的函数解析式为( )
A.y=
B.y=
C.y=3x
D.y=
6.已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=20v
B.t=
C.t=
D.t=
7.如图,菱形OABC在第一象限内,∠AOC=60°,反比例函数y=(x>0)的图象经过点A,交BC边于点D,若△AOD的面积为,则k的值为( )
A.
B.
C.
D.4
8.如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
A.(0,﹣)
B.(0,﹣)
C.(0,﹣3)
D.(0,﹣)
9.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
10.反比例函数y=与y=﹣kx+1(k≠0)在同一坐标系的图象可能为( )
A.
B.
C.
D.
二.填空题
11.我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙,比如,通过图中的信息,我们可以得出x>的解是
.
12.请写出一个图象在第二、四象限的反比例函数的表达式:
.
13.若函数y=(m﹣1)是反比例函数,则m的值等于
.
14.如图,一次函数y=mx与反比例函数y=的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=3,则k的值是
.
15.已知点A(a1,b1)与点B(a2,b2),两点都在反比例函数的图象上,且0<a1<a2,那么b1
b2.
16.已知与y=x﹣6相交于点P(a,b),则的值为
.
17.某食用油生产厂要制造一种容积为5升(1升=1立方分米)的圆柱形油桶,油桶的底面面积s与桶高h的函数关系式为
.
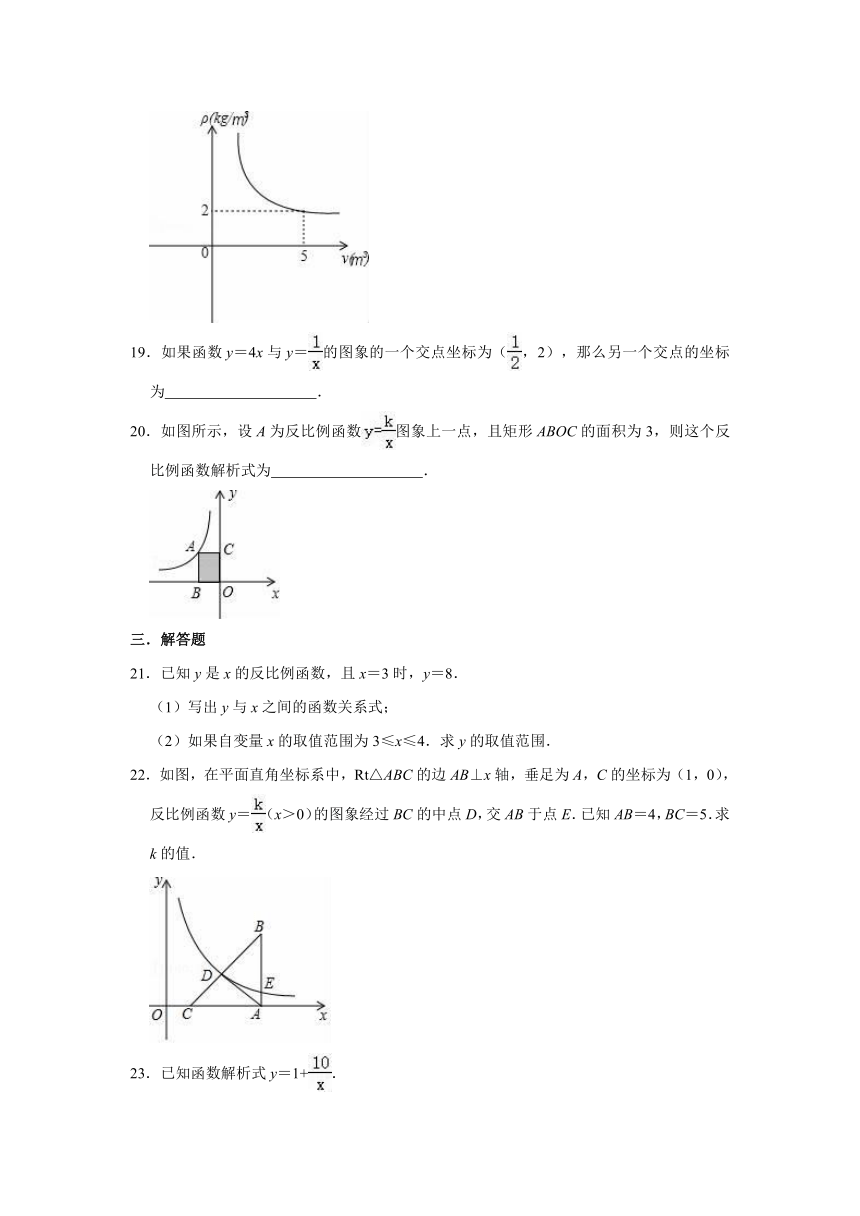
18.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是
m3.
19.如果函数y=4x与y=的图象的一个交点坐标为(,2),那么另一个交点的坐标为
.
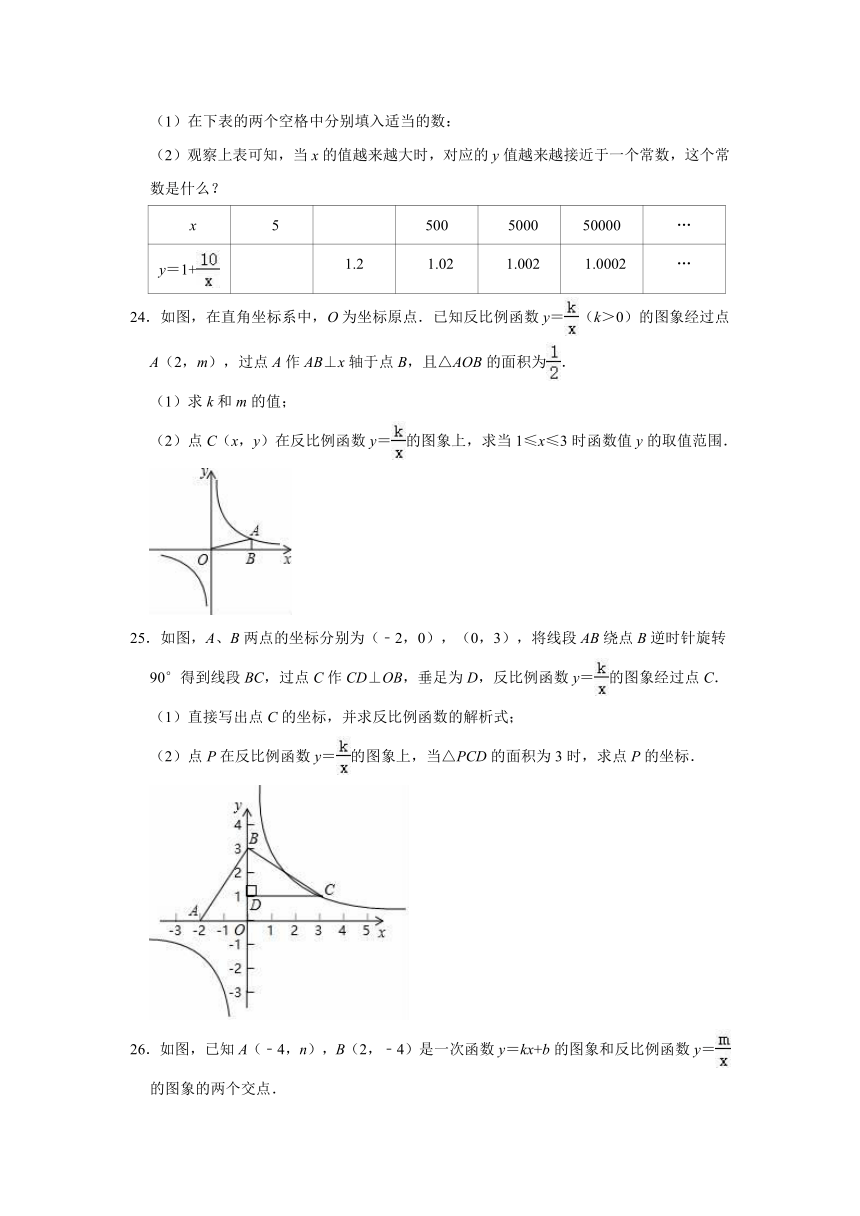
20.如图所示,设A为反比例函数图象上一点,且矩形ABOC的面积为3,则这个反比例函数解析式为
.
三.解答题
21.已知y是x的反比例函数,且x=3时,y=8.
(1)写出y与x之间的函数关系式;
(2)如果自变量x的取值范围为3≤x≤4.求y的取值范围.
22.如图,在平面直角坐标系中,Rt△ABC的边AB⊥x轴,垂足为A,C的坐标为(1,0),反比例函数y=(x>0)的图象经过BC的中点D,交AB于点E.已知AB=4,BC=5.求k的值.
23.已知函数解析式y=1+.
(1)在下表的两个空格中分别填入适当的数:
(2)观察上表可知,当x的值越来越大时,对应的y值越来越接近于一个常数,这个常数是什么?
x
5
500
5000
50000
…
y=1+
1.2
1.02
1.002
1.0002
…
24.如图,在直角坐标系中,O为坐标原点.已知反比例函数y=(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=的图象上,求当1≤x≤3时函数值y的取值范围.
25.如图,A、B两点的坐标分别为(﹣2,0),(0,3),将线段AB绕点B逆时针旋转90°得到线段BC,过点C作CD⊥OB,垂足为D,反比例函数y=的图象经过点C.
(1)直接写出点C的坐标,并求反比例函数的解析式;
(2)点P在反比例函数y=的图象上,当△PCD的面积为3时,求点P的坐标.
26.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
27.我们可以把一个假分数写成一个整数加上一个真分数的形式,如.同样的,我们也可以把某些分式写成类似的形式,如.这种方法我们称为“分离常数法”.
(1)如果,求常数a的值;
(2)利用分离常数法,解决下面的问题:
当m取哪些整数时,分式的值是整数?
(3)我们知道一次函数y=x﹣1的图象可以看成是由正比例函数y=x的图象向下平移1个单位长度得到,函数y=的图象可以看成是由反比例函数y=的图象向左平移1个单位长度得到.那么请你分析说明函数y=的图象是由哪个反比例函数的图象经过怎样的变换得到?
参考答案与试题解析
一.选择题
1.解:A、是正比例函数,故选项错误;
B、是反比例函数,故选项正确;
C、是正比例函数,故选项错误;
D、是二次函数,故选项错误.
故选:B.
2.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(2,3)关于原点对称,
∴该点的坐标为(﹣2,﹣3).
故选:D.
3.解:∵双曲线位于第二、四象限,
∴k﹣1<0,
∴k<1.
故选:A.
4.解:∵反比例函数的图象经过点P(1,2),
∴k=1×2=2>0,
∴此函数的图象位于一三象限.
故选:B.
5.解:设y=,
∵x=2,y=6,
∴6=,解得k=12,
∴y关于x的函数解析式为y=.
故选:D.
6.解:由题意得:vt=20,
t=,
故选:B.
7.解:如图,过点A作AE⊥OC于E,
∵四边形ABCO是菱形,
∴AO∥CB,OA=OC,且∠AOC=60°,
∴△AOC是等边三角形,且AE⊥OC,
∴S△AOE=S△AOC,
∵OA∥BC,
∴S△OAD=S△OAC=2,
∴S△AOE==,
∴k=2
故选:C.
8.解:∵正方形的顶点A(m,2),
∴正方形的边长为2,
∴BC=2,
而点E(n,),
∴n=2+m,即E点坐标为(2+m,),
∴k=2?m=(2+m),解得m=1,
∴A(1,2),E(3,),
∴B(1,0),D(3,2),
设直线BD的解析式为y=ax+b,
把B(1,0),D(3,2)代入得,
解得,
∵过点E作直线l∥BD交y轴于点F,
∴设直线l的解析式为y=x+q,
把E(3,)代入得3+q=,
解得q=﹣,
∴直线l的解析式为y=x﹣
当x=0时,y=﹣,
∴点F的坐标为(0,﹣),
故选:A.
9.解:设用电阻R表示电流I的函数解析式为I=,
∵过(2,3),
∴k=3×2=6,
∴I=,
故选:D.
10.解:A、由反比例函数的图象可知,k>0,一次函数图象呈上升趋势且交与y轴的正半轴,﹣k>0,即k<0,故本选项错误;
B、由反比例函数的图象可知,k>0,一次函数图象呈下降趋势且交与y轴的正半轴,﹣k<0,即k>0,故本选项正确;
C、由反比例函数的图象可知,k<0,一次函数图象呈上升趋势且交与y轴的负半轴(不合题意),故本选项错误;
D、由反比例函数的图象可知,k<0,一次函数图象呈下降趋势且交与y轴的正半轴,﹣k<0,即k>0,故本选项错误.
故选:B.
二.填空题
11.解:x>,在函数图象上则表示为相应的直线部分比双曲线部分高,两个交点的横坐标分别为﹣1,1;
从图象上可看出当x>时,应该位于交点的右边.
即x>1或﹣1<x<0.
12.解:∵图象在第二、四象限,
∴y=﹣,
故答案为:y=﹣.
13.解:∵y=(m﹣1)是反比例函数,
∴m2﹣2=﹣1,m﹣1≠0,
∴m=﹣1.
故答案为﹣1.
14.解:由题意得:S△ABM=2S△AOM=3,S△AOM=|k|=,则k=3.
故答案为:3.
15.解:∵k<0,
∴函数图象在二,四象限,
∵0<a1<a2,
∴两点都在第二象限,y随x的增大而增大,
∴b1<b2.
故答案为b1<b2.
16.解:∵函数与y=x﹣6相交于点P(a,b),
∴ab=1,b﹣a=﹣6,
∴﹣==﹣6,
故答案为﹣6
17.解:由题意得:油桶的底面面积s与桶高h的函数关系式为S=.
故本题答案为:S=.
18.解:设密度ρ与体积V的反比例函数解析式为ρ=,把点(5,2)代入解ρ=,得k=10,
∴密度ρ与体积V的反比例函数解析式为ρ=,把v=10代入ρ=,
得ρ=1m3.
故答案为:1.
19.解:∵两函数图象关于原点对称,
∴两函数图象交点关于原点对称,
∴(,2)的对称点为(﹣,﹣2).
故答案为(﹣,﹣2).
20.解:由题意得:S=|k|=3,则k=±3;
又由于反比例函数图象位于二、四象限,k<0,
则k=﹣3,反比例函数的解析式是:y=﹣.
故答案为:y=﹣.
三.解答题
21.解:(1)设反比例函数是y=(k≠0),
当x=3时,y=8,代入可解得k=24.
所以y=.
(2)当x=3时,y=8,当x=4时,y=6,
∴自变量x的取值范围为3≤x≤4.y的取值范围为6≤y≤8.
22.解:∵在Rt△ABC中,AB=4,BC=5
∴AC===3
∵点C坐标(1,0)
∴OC=1
∴OA=OC+AC=4
∴点A坐标(4,0)
∴点B(4,4)
∵点C(1,0),点B(4,4)
∴BC的中点D(,2)
∵反比例函数y=(x>0)的图象经过BC的中点D
∴2=
∴k=5
23.解:(1)x=5时,y=3;y=1.2时,x=50;
填入表格如下:
x
5
50
500
5000
50000
…
y=1+
3
1.2
1.02
1.002
1.0002
…
(2)由上表可知,当x的值越来越大时,对应的y值越来越接近于常数1.
24.解:(1)∵A(2,m),
∴OB=2,AB=m,
∴S△AOB=?OB?AB=×2×m=,
∴m=;
∴点A的坐标为(2,),
把A(2,)代入y=,得=,
∴k=1;
(2)∵当x=1时,y=1;当x=3时,y=,
又∵反比例函数y=在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为≤y≤1.
25.解:(1)∵将线段AB绕点B逆时针旋转90°得到线段BC,
∴AB=BC,∠ABC=90°,
∵CD⊥OB,
∴∠CDB=∠AOB=∠ABC=90°,
∴∠ABO+∠CBD=∠CBD+∠DCB=90°,
∴∠ABO=∠DCB,
∴△ABO≌△BCD(AAS),
∴CD=OB=3,BD=OA=2,
∴OD=3﹣2=1,
∴C点的坐标为(3,1),
∴k=3×1=3,
∴反比例函数的解析式为:;
(2)设P(,m),
∵CD⊥y轴,CD=3,
由△PCD的面积为3得:
CD?|m﹣1|=3,
∴×3|m﹣1|=3,
∴m﹣1=±2,
∴m=3或m=﹣1,
当m=3时,=1,当m=﹣1时,=﹣3,
∴点P的坐标为(1,3)或(﹣3,﹣1).
26.解:(1)把B(2,﹣4)代入y=得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把A(﹣4,n)代入y=﹣得﹣4n=﹣8,解得n=2,则A点坐标为(﹣4,2),
把A(﹣4,2)、B(2,﹣4)代入y=kx+b得,解得,
所以一次函数解析式为y=﹣x﹣2;
(2)把y=0代入y=﹣x﹣2得﹣x﹣2=0,解得x=﹣2,则C点坐标为(﹣2,0),
所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)﹣4<x<0或x>2.
27.(1)∵==1+,∴1+=1+,∴a=﹣4;
(2)式===﹣3﹣,
所以当m﹣1=3或﹣3或1或﹣1时,分式的值为整数,
解得m=4或m=﹣2或m=0或m=2;
(3)y====3+,
∴将y=的图象向右移动2个单位长度得到y=的图象,再向上移动3个单位长度得到y﹣3=,即y=.
反比例函数》单元测试卷
一.选择题
1.下列函数中,y是x的反比例函数的是( )
A.y=
B.y=
C.y=3x
D.y=x2
2.若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2,3),则另一个交点的坐标是( )
A.(2,3)
B.(3,2)
C.(﹣2,3)
D.(﹣2,﹣3)
3.若双曲线位于第二、四象限,则k的取值范围是( )
A.k<1
B.k≥1
C.k>1
D.k≠1
4.已知反比例函数的图象经过点P(1,2),则这个函数的图象位于( )
A.第二、三象限
B.第一、三象限
C.第二、四象限
D.第三、四象限
5.已知y是x的反比例函数,并且当x=2时,y=6,则y关于x的函数解析式为( )
A.y=
B.y=
C.y=3x
D.y=
6.已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=20v
B.t=
C.t=
D.t=
7.如图,菱形OABC在第一象限内,∠AOC=60°,反比例函数y=(x>0)的图象经过点A,交BC边于点D,若△AOD的面积为,则k的值为( )
A.
B.
C.
D.4
8.如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
A.(0,﹣)
B.(0,﹣)
C.(0,﹣3)
D.(0,﹣)
9.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
10.反比例函数y=与y=﹣kx+1(k≠0)在同一坐标系的图象可能为( )
A.
B.
C.
D.
二.填空题
11.我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙,比如,通过图中的信息,我们可以得出x>的解是
.
12.请写出一个图象在第二、四象限的反比例函数的表达式:
.
13.若函数y=(m﹣1)是反比例函数,则m的值等于
.
14.如图,一次函数y=mx与反比例函数y=的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=3,则k的值是
.
15.已知点A(a1,b1)与点B(a2,b2),两点都在反比例函数的图象上,且0<a1<a2,那么b1
b2.
16.已知与y=x﹣6相交于点P(a,b),则的值为
.
17.某食用油生产厂要制造一种容积为5升(1升=1立方分米)的圆柱形油桶,油桶的底面面积s与桶高h的函数关系式为
.
18.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是
m3.
19.如果函数y=4x与y=的图象的一个交点坐标为(,2),那么另一个交点的坐标为
.
20.如图所示,设A为反比例函数图象上一点,且矩形ABOC的面积为3,则这个反比例函数解析式为
.
三.解答题
21.已知y是x的反比例函数,且x=3时,y=8.
(1)写出y与x之间的函数关系式;
(2)如果自变量x的取值范围为3≤x≤4.求y的取值范围.
22.如图,在平面直角坐标系中,Rt△ABC的边AB⊥x轴,垂足为A,C的坐标为(1,0),反比例函数y=(x>0)的图象经过BC的中点D,交AB于点E.已知AB=4,BC=5.求k的值.
23.已知函数解析式y=1+.
(1)在下表的两个空格中分别填入适当的数:
(2)观察上表可知,当x的值越来越大时,对应的y值越来越接近于一个常数,这个常数是什么?
x
5
500
5000
50000
…
y=1+
1.2
1.02
1.002
1.0002
…
24.如图,在直角坐标系中,O为坐标原点.已知反比例函数y=(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=的图象上,求当1≤x≤3时函数值y的取值范围.
25.如图,A、B两点的坐标分别为(﹣2,0),(0,3),将线段AB绕点B逆时针旋转90°得到线段BC,过点C作CD⊥OB,垂足为D,反比例函数y=的图象经过点C.
(1)直接写出点C的坐标,并求反比例函数的解析式;
(2)点P在反比例函数y=的图象上,当△PCD的面积为3时,求点P的坐标.
26.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
27.我们可以把一个假分数写成一个整数加上一个真分数的形式,如.同样的,我们也可以把某些分式写成类似的形式,如.这种方法我们称为“分离常数法”.
(1)如果,求常数a的值;
(2)利用分离常数法,解决下面的问题:
当m取哪些整数时,分式的值是整数?
(3)我们知道一次函数y=x﹣1的图象可以看成是由正比例函数y=x的图象向下平移1个单位长度得到,函数y=的图象可以看成是由反比例函数y=的图象向左平移1个单位长度得到.那么请你分析说明函数y=的图象是由哪个反比例函数的图象经过怎样的变换得到?
参考答案与试题解析
一.选择题
1.解:A、是正比例函数,故选项错误;
B、是反比例函数,故选项正确;
C、是正比例函数,故选项错误;
D、是二次函数,故选项错误.
故选:B.
2.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(2,3)关于原点对称,
∴该点的坐标为(﹣2,﹣3).
故选:D.
3.解:∵双曲线位于第二、四象限,
∴k﹣1<0,
∴k<1.
故选:A.
4.解:∵反比例函数的图象经过点P(1,2),
∴k=1×2=2>0,
∴此函数的图象位于一三象限.
故选:B.
5.解:设y=,
∵x=2,y=6,
∴6=,解得k=12,
∴y关于x的函数解析式为y=.
故选:D.
6.解:由题意得:vt=20,
t=,
故选:B.
7.解:如图,过点A作AE⊥OC于E,
∵四边形ABCO是菱形,
∴AO∥CB,OA=OC,且∠AOC=60°,
∴△AOC是等边三角形,且AE⊥OC,
∴S△AOE=S△AOC,
∵OA∥BC,
∴S△OAD=S△OAC=2,
∴S△AOE==,
∴k=2
故选:C.
8.解:∵正方形的顶点A(m,2),
∴正方形的边长为2,
∴BC=2,
而点E(n,),
∴n=2+m,即E点坐标为(2+m,),
∴k=2?m=(2+m),解得m=1,
∴A(1,2),E(3,),
∴B(1,0),D(3,2),
设直线BD的解析式为y=ax+b,
把B(1,0),D(3,2)代入得,
解得,
∵过点E作直线l∥BD交y轴于点F,
∴设直线l的解析式为y=x+q,
把E(3,)代入得3+q=,
解得q=﹣,
∴直线l的解析式为y=x﹣
当x=0时,y=﹣,
∴点F的坐标为(0,﹣),
故选:A.
9.解:设用电阻R表示电流I的函数解析式为I=,
∵过(2,3),
∴k=3×2=6,
∴I=,
故选:D.
10.解:A、由反比例函数的图象可知,k>0,一次函数图象呈上升趋势且交与y轴的正半轴,﹣k>0,即k<0,故本选项错误;
B、由反比例函数的图象可知,k>0,一次函数图象呈下降趋势且交与y轴的正半轴,﹣k<0,即k>0,故本选项正确;
C、由反比例函数的图象可知,k<0,一次函数图象呈上升趋势且交与y轴的负半轴(不合题意),故本选项错误;
D、由反比例函数的图象可知,k<0,一次函数图象呈下降趋势且交与y轴的正半轴,﹣k<0,即k>0,故本选项错误.
故选:B.
二.填空题
11.解:x>,在函数图象上则表示为相应的直线部分比双曲线部分高,两个交点的横坐标分别为﹣1,1;
从图象上可看出当x>时,应该位于交点的右边.
即x>1或﹣1<x<0.
12.解:∵图象在第二、四象限,
∴y=﹣,
故答案为:y=﹣.
13.解:∵y=(m﹣1)是反比例函数,
∴m2﹣2=﹣1,m﹣1≠0,
∴m=﹣1.
故答案为﹣1.
14.解:由题意得:S△ABM=2S△AOM=3,S△AOM=|k|=,则k=3.
故答案为:3.
15.解:∵k<0,
∴函数图象在二,四象限,
∵0<a1<a2,
∴两点都在第二象限,y随x的增大而增大,
∴b1<b2.
故答案为b1<b2.
16.解:∵函数与y=x﹣6相交于点P(a,b),
∴ab=1,b﹣a=﹣6,
∴﹣==﹣6,
故答案为﹣6
17.解:由题意得:油桶的底面面积s与桶高h的函数关系式为S=.
故本题答案为:S=.
18.解:设密度ρ与体积V的反比例函数解析式为ρ=,把点(5,2)代入解ρ=,得k=10,
∴密度ρ与体积V的反比例函数解析式为ρ=,把v=10代入ρ=,
得ρ=1m3.
故答案为:1.
19.解:∵两函数图象关于原点对称,
∴两函数图象交点关于原点对称,
∴(,2)的对称点为(﹣,﹣2).
故答案为(﹣,﹣2).
20.解:由题意得:S=|k|=3,则k=±3;
又由于反比例函数图象位于二、四象限,k<0,
则k=﹣3,反比例函数的解析式是:y=﹣.
故答案为:y=﹣.
三.解答题
21.解:(1)设反比例函数是y=(k≠0),
当x=3时,y=8,代入可解得k=24.
所以y=.
(2)当x=3时,y=8,当x=4时,y=6,
∴自变量x的取值范围为3≤x≤4.y的取值范围为6≤y≤8.
22.解:∵在Rt△ABC中,AB=4,BC=5
∴AC===3
∵点C坐标(1,0)
∴OC=1
∴OA=OC+AC=4
∴点A坐标(4,0)
∴点B(4,4)
∵点C(1,0),点B(4,4)
∴BC的中点D(,2)
∵反比例函数y=(x>0)的图象经过BC的中点D
∴2=
∴k=5
23.解:(1)x=5时,y=3;y=1.2时,x=50;
填入表格如下:
x
5
50
500
5000
50000
…
y=1+
3
1.2
1.02
1.002
1.0002
…
(2)由上表可知,当x的值越来越大时,对应的y值越来越接近于常数1.
24.解:(1)∵A(2,m),
∴OB=2,AB=m,
∴S△AOB=?OB?AB=×2×m=,
∴m=;
∴点A的坐标为(2,),
把A(2,)代入y=,得=,
∴k=1;
(2)∵当x=1时,y=1;当x=3时,y=,
又∵反比例函数y=在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为≤y≤1.
25.解:(1)∵将线段AB绕点B逆时针旋转90°得到线段BC,
∴AB=BC,∠ABC=90°,
∵CD⊥OB,
∴∠CDB=∠AOB=∠ABC=90°,
∴∠ABO+∠CBD=∠CBD+∠DCB=90°,
∴∠ABO=∠DCB,
∴△ABO≌△BCD(AAS),
∴CD=OB=3,BD=OA=2,
∴OD=3﹣2=1,
∴C点的坐标为(3,1),
∴k=3×1=3,
∴反比例函数的解析式为:;
(2)设P(,m),
∵CD⊥y轴,CD=3,
由△PCD的面积为3得:
CD?|m﹣1|=3,
∴×3|m﹣1|=3,
∴m﹣1=±2,
∴m=3或m=﹣1,
当m=3时,=1,当m=﹣1时,=﹣3,
∴点P的坐标为(1,3)或(﹣3,﹣1).
26.解:(1)把B(2,﹣4)代入y=得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把A(﹣4,n)代入y=﹣得﹣4n=﹣8,解得n=2,则A点坐标为(﹣4,2),
把A(﹣4,2)、B(2,﹣4)代入y=kx+b得,解得,
所以一次函数解析式为y=﹣x﹣2;
(2)把y=0代入y=﹣x﹣2得﹣x﹣2=0,解得x=﹣2,则C点坐标为(﹣2,0),
所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)﹣4<x<0或x>2.
27.(1)∵==1+,∴1+=1+,∴a=﹣4;
(2)式===﹣3﹣,
所以当m﹣1=3或﹣3或1或﹣1时,分式的值为整数,
解得m=4或m=﹣2或m=0或m=2;
(3)y====3+,
∴将y=的图象向右移动2个单位长度得到y=的图象,再向上移动3个单位长度得到y﹣3=,即y=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
