2021-2022学年青岛新版八年级上册数学《第1章 全等三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年青岛新版八年级上册数学《第1章 全等三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:46:59 | ||
图片预览

文档简介
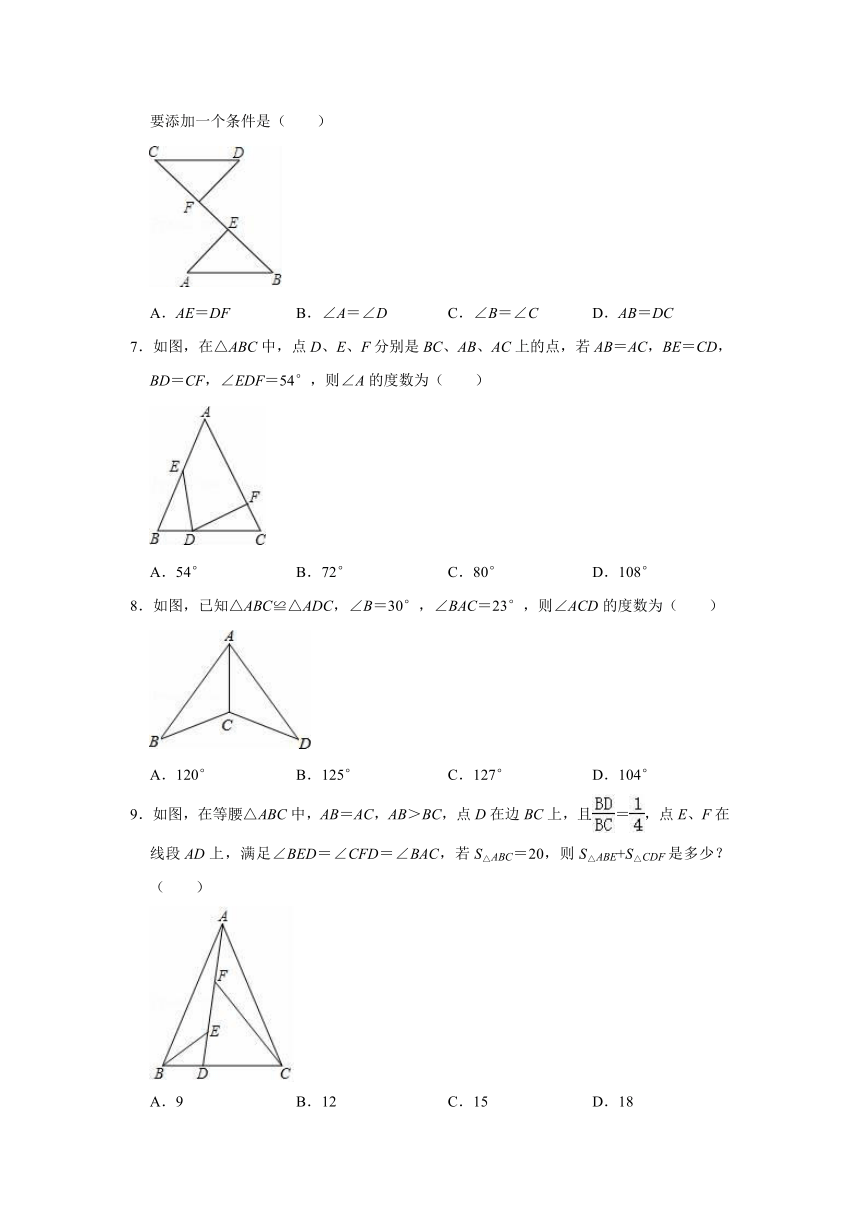
2021-2022学年青岛新版八年级上册数学《第1章
全等三角形》单元测试卷
一.选择题
1.下列图形中,属于全等形的是( )
A.
B.
C.
D.
2.已知图中的两个三角形全等,则∠α度数是( )
A.50°
B.58°
C.60°
D.72°
3.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
A.∠ADB=∠ADC
B.∠B=∠C
C.DB=DC
D.AB=AC
4.下列条件不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一条直角边和它所对的锐角对应相等
D.一个锐角和锐角所对的直角边对应相等
5.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
6.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=DC
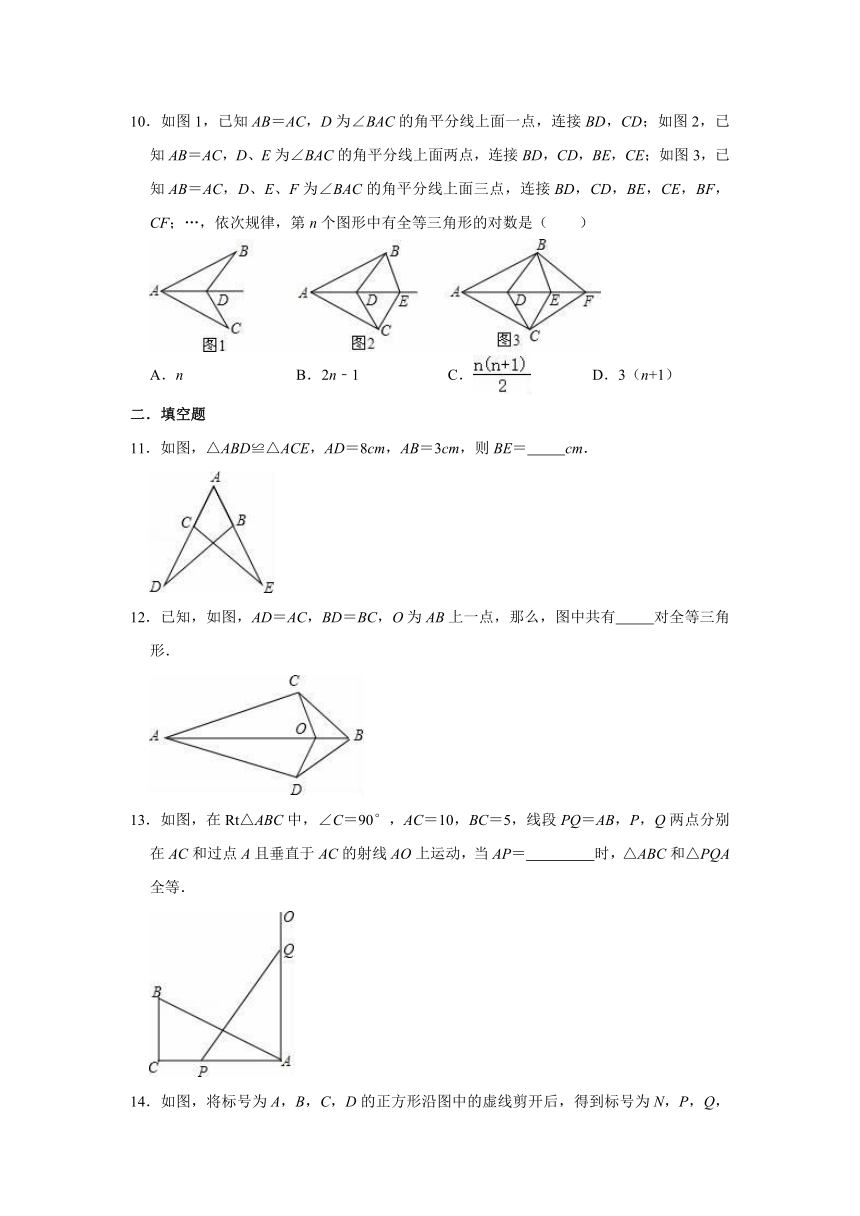
7.如图,在△ABC中,点D、E、F分别是BC、AB、AC上的点,若AB=AC,BE=CD,BD=CF,∠EDF=54°,则∠A的度数为( )
A.54°
B.72°
C.80°
D.108°
8.如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
A.120°
B.125°
C.127°
D.104°
9.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+S△CDF是多少?( )
A.9
B.12
C.15
D.18
10.如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是( )
A.n
B.2n﹣1
C.
D.3(n+1)
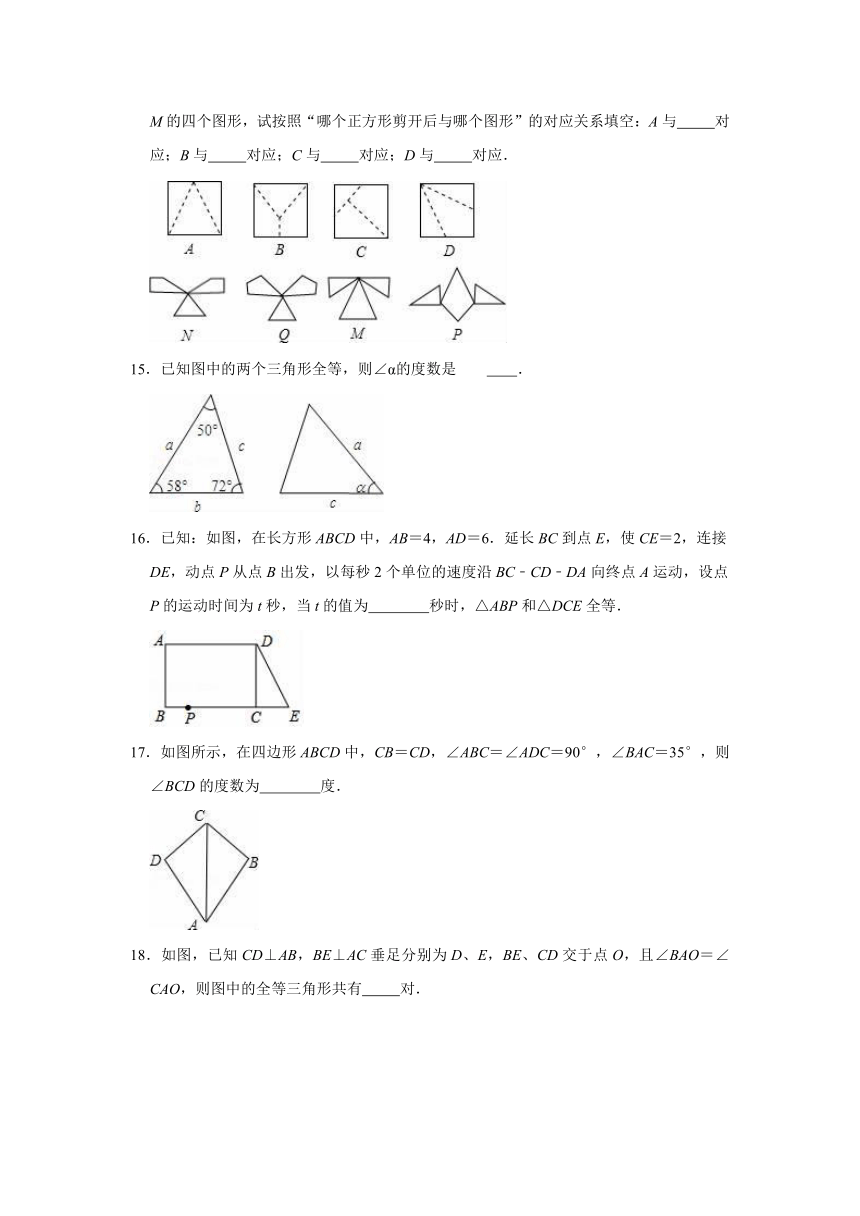
二.填空题
11.如图,△ABD≌△ACE,AD=8cm,AB=3cm,则BE=
cm.
12.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有
对全等三角形.
13.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC和△PQA全等.
14.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与
对应;B与
对应;C与
对应;D与
对应.
15.已知图中的两个三角形全等,则∠α的度数是
.
16.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为
秒时,△ABP和△DCE全等.
17.如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为
度.
18.如图,已知CD⊥AB,BE⊥AC垂足分别为D、E,BE、CD交于点O,且∠BAO=∠CAO,则图中的全等三角形共有
对.
19.如图,在平面直角坐标系中,已知点A(0,3),点B(9,0),且∠ACB=90°,CA=CB,则点C的坐标为
.
20.如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计)
.
三.解答题
21.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
22.已知:如图,点A、D、B、E在同一条直线上,AC=DF,AC∥DF,AD=BE.求证:△ABC≌△DEF.
23.如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
24.如图,线段AC交BD于O,点E,F在线段AC上,△DFO≌△BEO,且AF=CE,连接AB、CD,求证:AB=CD.
25.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中的道理吗?
26.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是
.(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
27.如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
参考答案与试题解析
一.选择题
1.解:A、两个正方形的边长不相等,不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确.
C、两图形不能完全重合,故本选项错误;
D、两图形不能完全重合,故本选项错误.
故选:B.
2.解:∵两个三角形全等,
∴α=50°.
故选:A.
3.解:A、加∠ADB=∠ADC,∵∠1=∠2,AD=AD,∠ADB=∠ADC,∴△ABD≌△ACD(ASA),是正确选法;
B、加∠B=∠C∵∠1=∠2,AD=AD,∠B=∠C,∴△ABD≌△ACD(AAS),是正确选法;
C、加DB=DC,满足SSA,不能得出△ABD≌△ACD,是错误选法;
D、加AB=AC,∵∠1=∠2,AD=AD,AB=AC,∴△ABD≌△ACD(SAS),是正确选法.
故选:C.
4.解:A、两条直角边对应相等,可利用全等三角形的判定定理SAS来判定两直角三角形全等,故本选项正确;
B、两个锐角对应相等,再由两个直角三角形的两个直角相等,AAA没有边的参与,所以不能判定两个直角三角形全等;故本选项错误;
C、一条直角边和它所对的锐角对应相等,可利用全等三角形的判定定理ASA来判定两个直角三角形全等;故本选项正确;
D、一个锐角和锐角所对的直角边对应相等,可以利用全等三角形的判定定理ASA或AAS来判定两个直角三角形全等;故本选项正确;
故选:B.
5.解:A:两个面积相等的图形不一定是全等图形,故A错误;
B:长方形不一定是全等图形,故B错误;
C:两个全等图形形状一定相同,故C正确;
D:两个正方形不一定是全等图形,故D错误;
故选:C.
6.解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故选:D.
7.解:∵AB=AC,
∴∠B=∠C,
在△BDE和△CFD中
,
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF,∠BDE=∠CFD,
∴∠BED+∠BDE=∠CDF+∠CFD,
∵∠BED+∠BDE+∠B=∠CDF+∠CFD+∠EDF=180°,
∴∠B=∠EDF=54°,
∴∠A=180°﹣2×54°=72°,
故选:B.
8.解:∵∠B=30°,∠BAC=23°,
∴∠ACB=180°﹣30°﹣23°=127°,
∵△ABC≌△ADC,
∴∠ACD=∠ACB=127°,
故选:C.
9.解:∵∠BED=∠CFD=∠BAC,∠BED=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠CFD=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∵,
∴△ABE≌△CAF(ASA),
∴S△ABE=S△ACF,
∴S△ABE+S△CDF=S△ACD
∵S△ABC=20,=,
∴S△ACD=15,
故选:C.
10.解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD.
∴图1中有1对三角形全等;
同理图2中,△ABE≌△ACE,
∴BE=EC,
∵△ABD≌△ACD.
∴BD=CD,
又DE=DE,
∴△BDE≌△CDE,
∴图2中有3对三角形全等;
同理:图3中有6对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
二.填空题
11.解:∵△ABD≌△ACE,
∴AD=AE,AC=AB,
又AD=8cm,AB=3cm,
∵BE=AE﹣AB=8﹣3=5,
∴BE=5cm.
故填5.
12.解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为:3.
13.解:当AP=5或10时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=5=BC时,
在Rt△ACB和Rt△QAP中
∴Rt△ACB≌Rt△QAP(HL),
②当AP=10=AC时,
在Rt△ACB和Rt△PAQ中
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:5或10.
14.解:由全等形的概念可知:
A是三个三角形,与M对应;
B是一个三角形和两个直角梯形,与N对应;
C是一个三角形和两个四边形,与Q对应;
D是两个三角形和一个四边形,与P对应
故分别填入M,N,Q,P.
15.解:∵两个三角形全等,
∴α=50°.
故答案为:50°.
16.解:
设点P的运动时间为t秒,则BP=2t,
当点P在线段BC上时,
∵四边形ABCD为长方形,
∴AB=CD,∠B=∠DCE=90°,
此时有△ABP≌△DCE,
∴BP=CE,即2t=2,解得t=1;
当点P在线段AD上时,
∵AB=4,AD=6,
∴BC=6,CD=4,
∴AP=BC+CD+DA=6+4+6=16,
∴AP=16﹣2t,
此时有△ABP≌△CDE,
∴AP=CE,即16﹣2t=2,解得t=7;
综上可知当t为1秒或7秒时,△ABP和△CDE全等.
故答案为:1或7.
17.解:∵∠ABC=∠ADC=90°,CB=CD,且CA=CA
∴△ABC≌△ADC
∴∠BCA=∠DCA
∵∠BAC=35°,∠ABC=90°
∴∠BCA=55°
∴∠BCD=2∠BCA=110°.
故答案为:110°.
18.解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°,
∵AO=AO,∠DAO=∠EAO,
∴△ADO≌△AEO(AAS);
∴OD=OE,AD=AE,
∵∠DOB=∠EOC,∠ODB=∠OEC=90°,
∴△BOD≌△COE(ASA);
∴BD=CE,OB=OC,∠B=∠C;
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°;
∴△ADC≌△AEB(ASA);
∵AD=AE,BD=CE;
∴AB=AC;
∵OB=OC,AO=AO;
∴△ABO≌△ACO(SSS).
所以共有四对全等三角形.
故答案为:四.
19.解:如图,过点C作CE⊥OA,CF⊥OB,
∵∠AOB=90°,
∴四边形OECF是矩形,
∴∠ECF=90°,
∵∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,,
∴△ACE≌△BCF,
∴CE=CF,
∵四边形OECF是矩形,
∴矩形OECF是正方形,
∴OE=OF,
∵AE=OE﹣OA=OE﹣3,BF=OB﹣OF=9﹣OF,
∴OE=OF=6,
∴C(6,6),
故答案为:(6,6);
20.解:∵后面画出的图形与第一个图形完全一样
∴画第二个图形的时候,需往右用1个格,画第三个图的时候,需要再往右用三个格,画第四个图的时候,需要再往右走1个格…
∴画第10个图时,网格的长为4+(1+3+1+3+1+3+1+3+1)=21个.
三.解答题
21.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
22.证明:∵AC∥DF,
∴∠A=∠EDF.
∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,AC=DF,∠A=∠EDF,AB=DE,
∴△ABC≌△DEF.
23.解:猜想:BF⊥AE.
理由:∵∠ACB=90°,
∴∠ACE=∠BCD=90°.
又BC=AC,BD=AE,
∴△BDC≌△AEC(HL).
∴∠CBD=∠CAE.
又∵∠CAE+∠E=90°.
∴∠EBF+∠E=90°.
∴∠BFE=90°,即BF⊥AE.
24.证明:∵△BEO≌△DFO,
∴OF=OE,DO=BO,
又∵AF=CE,
∴AO=CO,
在△ABO和△CDO中,
,
∴△ABO≌△CDO(SAS),
∴AB=CD.
25.解:∵在△BDE和△FDM中,
∴△BDE≌△FDM(SAS),
∴∠BEM=∠FME,
∴BE∥MF,
∵AB∥MF,
∴A、C、E三点在一条直线上.
26.解:(1)符合要求的条件是①②④,
故答案为:①②④;
(2)选④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,
∵∠BCD=∠B′C′D′,
∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,
∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,
即∠BAD=∠B′A′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
27.解:图象如图所示,
∵∠EAC=∠ACB,
∴AD∥CB,
∵AD=BC,∠DAC=∠ACB,AC=CA,
∴△ACD≌△CAB(SAS),
∴∠ACD=∠CAB,
∴AB∥CD.
全等三角形》单元测试卷
一.选择题
1.下列图形中,属于全等形的是( )
A.
B.
C.
D.
2.已知图中的两个三角形全等,则∠α度数是( )
A.50°
B.58°
C.60°
D.72°
3.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
A.∠ADB=∠ADC
B.∠B=∠C
C.DB=DC
D.AB=AC
4.下列条件不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一条直角边和它所对的锐角对应相等
D.一个锐角和锐角所对的直角边对应相等
5.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
6.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=DC
7.如图,在△ABC中,点D、E、F分别是BC、AB、AC上的点,若AB=AC,BE=CD,BD=CF,∠EDF=54°,则∠A的度数为( )
A.54°
B.72°
C.80°
D.108°
8.如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
A.120°
B.125°
C.127°
D.104°
9.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+S△CDF是多少?( )
A.9
B.12
C.15
D.18
10.如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是( )
A.n
B.2n﹣1
C.
D.3(n+1)
二.填空题
11.如图,△ABD≌△ACE,AD=8cm,AB=3cm,则BE=
cm.
12.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有
对全等三角形.
13.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC和△PQA全等.
14.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与
对应;B与
对应;C与
对应;D与
对应.
15.已知图中的两个三角形全等,则∠α的度数是
.
16.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为
秒时,△ABP和△DCE全等.
17.如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为
度.
18.如图,已知CD⊥AB,BE⊥AC垂足分别为D、E,BE、CD交于点O,且∠BAO=∠CAO,则图中的全等三角形共有
对.
19.如图,在平面直角坐标系中,已知点A(0,3),点B(9,0),且∠ACB=90°,CA=CB,则点C的坐标为
.
20.如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计)
.
三.解答题
21.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
22.已知:如图,点A、D、B、E在同一条直线上,AC=DF,AC∥DF,AD=BE.求证:△ABC≌△DEF.
23.如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
24.如图,线段AC交BD于O,点E,F在线段AC上,△DFO≌△BEO,且AF=CE,连接AB、CD,求证:AB=CD.
25.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中的道理吗?
26.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是
.(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
27.如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
参考答案与试题解析
一.选择题
1.解:A、两个正方形的边长不相等,不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确.
C、两图形不能完全重合,故本选项错误;
D、两图形不能完全重合,故本选项错误.
故选:B.
2.解:∵两个三角形全等,
∴α=50°.
故选:A.
3.解:A、加∠ADB=∠ADC,∵∠1=∠2,AD=AD,∠ADB=∠ADC,∴△ABD≌△ACD(ASA),是正确选法;
B、加∠B=∠C∵∠1=∠2,AD=AD,∠B=∠C,∴△ABD≌△ACD(AAS),是正确选法;
C、加DB=DC,满足SSA,不能得出△ABD≌△ACD,是错误选法;
D、加AB=AC,∵∠1=∠2,AD=AD,AB=AC,∴△ABD≌△ACD(SAS),是正确选法.
故选:C.
4.解:A、两条直角边对应相等,可利用全等三角形的判定定理SAS来判定两直角三角形全等,故本选项正确;
B、两个锐角对应相等,再由两个直角三角形的两个直角相等,AAA没有边的参与,所以不能判定两个直角三角形全等;故本选项错误;
C、一条直角边和它所对的锐角对应相等,可利用全等三角形的判定定理ASA来判定两个直角三角形全等;故本选项正确;
D、一个锐角和锐角所对的直角边对应相等,可以利用全等三角形的判定定理ASA或AAS来判定两个直角三角形全等;故本选项正确;
故选:B.
5.解:A:两个面积相等的图形不一定是全等图形,故A错误;
B:长方形不一定是全等图形,故B错误;
C:两个全等图形形状一定相同,故C正确;
D:两个正方形不一定是全等图形,故D错误;
故选:C.
6.解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故选:D.
7.解:∵AB=AC,
∴∠B=∠C,
在△BDE和△CFD中
,
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF,∠BDE=∠CFD,
∴∠BED+∠BDE=∠CDF+∠CFD,
∵∠BED+∠BDE+∠B=∠CDF+∠CFD+∠EDF=180°,
∴∠B=∠EDF=54°,
∴∠A=180°﹣2×54°=72°,
故选:B.
8.解:∵∠B=30°,∠BAC=23°,
∴∠ACB=180°﹣30°﹣23°=127°,
∵△ABC≌△ADC,
∴∠ACD=∠ACB=127°,
故选:C.
9.解:∵∠BED=∠CFD=∠BAC,∠BED=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠CFD=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∵,
∴△ABE≌△CAF(ASA),
∴S△ABE=S△ACF,
∴S△ABE+S△CDF=S△ACD
∵S△ABC=20,=,
∴S△ACD=15,
故选:C.
10.解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD.
∴图1中有1对三角形全等;
同理图2中,△ABE≌△ACE,
∴BE=EC,
∵△ABD≌△ACD.
∴BD=CD,
又DE=DE,
∴△BDE≌△CDE,
∴图2中有3对三角形全等;
同理:图3中有6对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
二.填空题
11.解:∵△ABD≌△ACE,
∴AD=AE,AC=AB,
又AD=8cm,AB=3cm,
∵BE=AE﹣AB=8﹣3=5,
∴BE=5cm.
故填5.
12.解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为:3.
13.解:当AP=5或10时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=5=BC时,
在Rt△ACB和Rt△QAP中
∴Rt△ACB≌Rt△QAP(HL),
②当AP=10=AC时,
在Rt△ACB和Rt△PAQ中
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:5或10.
14.解:由全等形的概念可知:
A是三个三角形,与M对应;
B是一个三角形和两个直角梯形,与N对应;
C是一个三角形和两个四边形,与Q对应;
D是两个三角形和一个四边形,与P对应
故分别填入M,N,Q,P.
15.解:∵两个三角形全等,
∴α=50°.
故答案为:50°.
16.解:
设点P的运动时间为t秒,则BP=2t,
当点P在线段BC上时,
∵四边形ABCD为长方形,
∴AB=CD,∠B=∠DCE=90°,
此时有△ABP≌△DCE,
∴BP=CE,即2t=2,解得t=1;
当点P在线段AD上时,
∵AB=4,AD=6,
∴BC=6,CD=4,
∴AP=BC+CD+DA=6+4+6=16,
∴AP=16﹣2t,
此时有△ABP≌△CDE,
∴AP=CE,即16﹣2t=2,解得t=7;
综上可知当t为1秒或7秒时,△ABP和△CDE全等.
故答案为:1或7.
17.解:∵∠ABC=∠ADC=90°,CB=CD,且CA=CA
∴△ABC≌△ADC
∴∠BCA=∠DCA
∵∠BAC=35°,∠ABC=90°
∴∠BCA=55°
∴∠BCD=2∠BCA=110°.
故答案为:110°.
18.解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°,
∵AO=AO,∠DAO=∠EAO,
∴△ADO≌△AEO(AAS);
∴OD=OE,AD=AE,
∵∠DOB=∠EOC,∠ODB=∠OEC=90°,
∴△BOD≌△COE(ASA);
∴BD=CE,OB=OC,∠B=∠C;
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°;
∴△ADC≌△AEB(ASA);
∵AD=AE,BD=CE;
∴AB=AC;
∵OB=OC,AO=AO;
∴△ABO≌△ACO(SSS).
所以共有四对全等三角形.
故答案为:四.
19.解:如图,过点C作CE⊥OA,CF⊥OB,
∵∠AOB=90°,
∴四边形OECF是矩形,
∴∠ECF=90°,
∵∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,,
∴△ACE≌△BCF,
∴CE=CF,
∵四边形OECF是矩形,
∴矩形OECF是正方形,
∴OE=OF,
∵AE=OE﹣OA=OE﹣3,BF=OB﹣OF=9﹣OF,
∴OE=OF=6,
∴C(6,6),
故答案为:(6,6);
20.解:∵后面画出的图形与第一个图形完全一样
∴画第二个图形的时候,需往右用1个格,画第三个图的时候,需要再往右用三个格,画第四个图的时候,需要再往右走1个格…
∴画第10个图时,网格的长为4+(1+3+1+3+1+3+1+3+1)=21个.
三.解答题
21.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
22.证明:∵AC∥DF,
∴∠A=∠EDF.
∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,AC=DF,∠A=∠EDF,AB=DE,
∴△ABC≌△DEF.
23.解:猜想:BF⊥AE.
理由:∵∠ACB=90°,
∴∠ACE=∠BCD=90°.
又BC=AC,BD=AE,
∴△BDC≌△AEC(HL).
∴∠CBD=∠CAE.
又∵∠CAE+∠E=90°.
∴∠EBF+∠E=90°.
∴∠BFE=90°,即BF⊥AE.
24.证明:∵△BEO≌△DFO,
∴OF=OE,DO=BO,
又∵AF=CE,
∴AO=CO,
在△ABO和△CDO中,
,
∴△ABO≌△CDO(SAS),
∴AB=CD.
25.解:∵在△BDE和△FDM中,
∴△BDE≌△FDM(SAS),
∴∠BEM=∠FME,
∴BE∥MF,
∵AB∥MF,
∴A、C、E三点在一条直线上.
26.解:(1)符合要求的条件是①②④,
故答案为:①②④;
(2)选④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,
∵∠BCD=∠B′C′D′,
∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,
∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,
即∠BAD=∠B′A′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
27.解:图象如图所示,
∵∠EAC=∠ACB,
∴AD∥CB,
∵AD=BC,∠DAC=∠ACB,AC=CA,
∴△ACD≌△CAB(SAS),
∴∠ACD=∠CAB,
∴AB∥CD.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
