2021年暑假自学八年级数学北师大版上册 《1.2一定是直角三角形吗》优生辅导训练 (word版含解析)
文档属性
| 名称 | 2021年暑假自学八年级数学北师大版上册 《1.2一定是直角三角形吗》优生辅导训练 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 234.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览


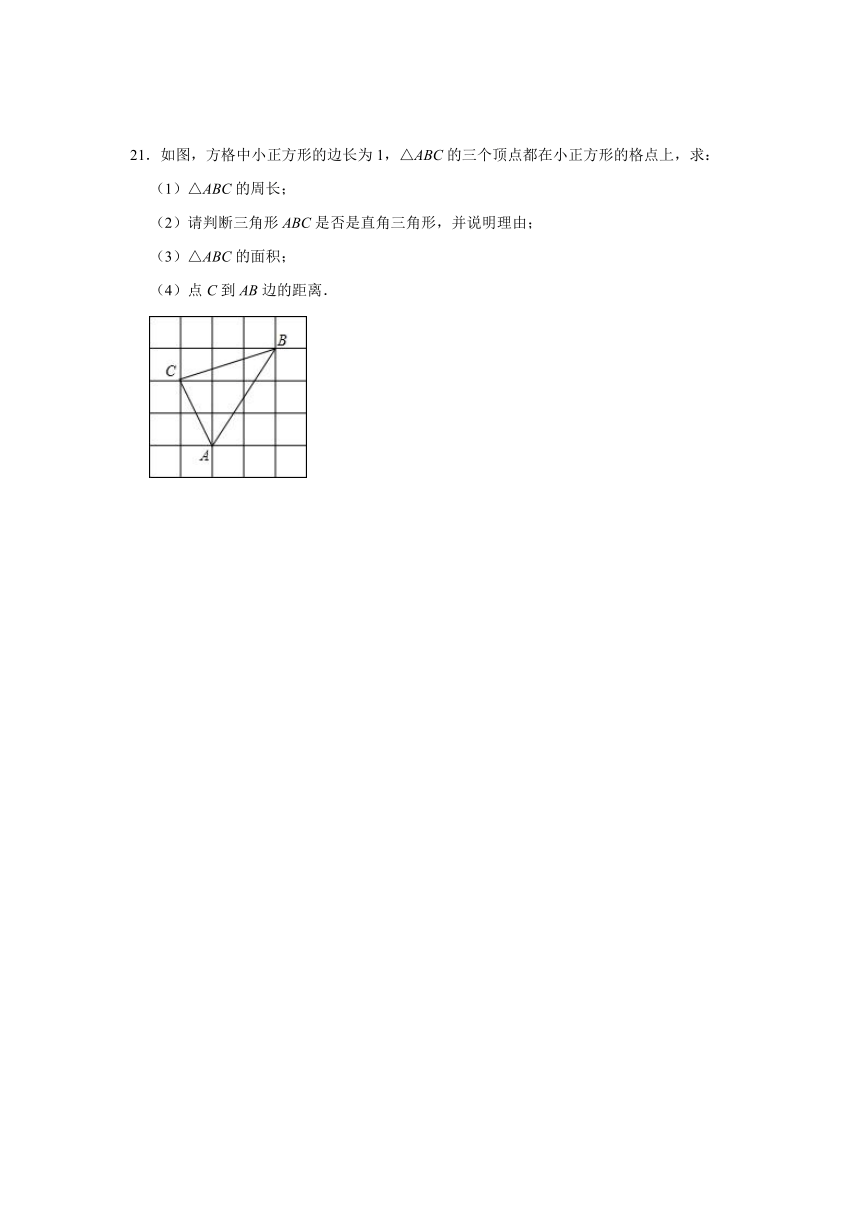
文档简介
2021年北师大版八年级数学上册《1.2一定是直角三角形吗》
暑假自学优生辅导训练(附答案)
1.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2 D.a:b:c=3:4:6
2.若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
3.下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
4.下列各组数中,是勾股数的为( )
A.1,1,2 B.1.5,2,2.5 C.7,24,25 D.6,12,13
5.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.以上答案都不对
6.如图,直线AB∥CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是( )
A.10cm B.12cm C.13cm D.14cm
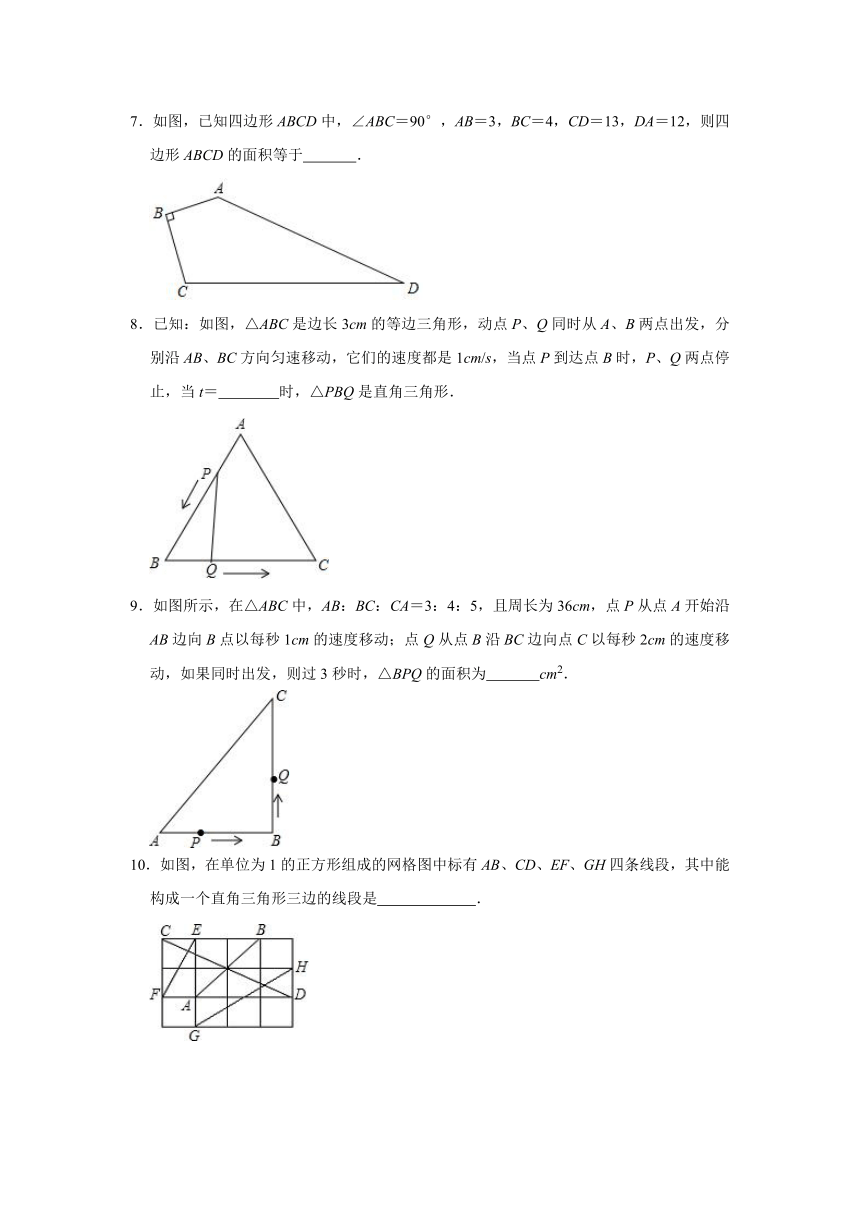
7.如图,已知四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=13,DA=12,则四边形ABCD的面积等于 .
8.已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止,当t= 时,△PBQ是直角三角形.
9.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为 cm2.
10.如图,在单位为1的正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是 .
11.如图,点A、B、C分别是正方体展开图的小正方形的顶点,则∠BAC的大小为 .
12.如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,该图形的面积等于 .
13.三角形的两边长分别为1cm和2cm,要使这个三角形是直角三角形,则第三条边长是 cm.
14.观察下列勾股数:
3,4,5;5,12,13;7,24,25;9,40,41;…:a,b,c.
根据你发现的规律,请写出:
(1)当a=19时,b= ,c= ;
(2)当a=2n+1时,求b、c的值;
(3)用(2)的结论判断15,111,112是否为一组勾股数,并说明理由.
15.如图,在△ABC中,∠ABC=∠ACB,AC=3,D是CA延长线上一点,AD=5,BD=4.求证:AB⊥BD.
16.如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长;
(2)若E是边AB上的动点,求线段DE的最小值.
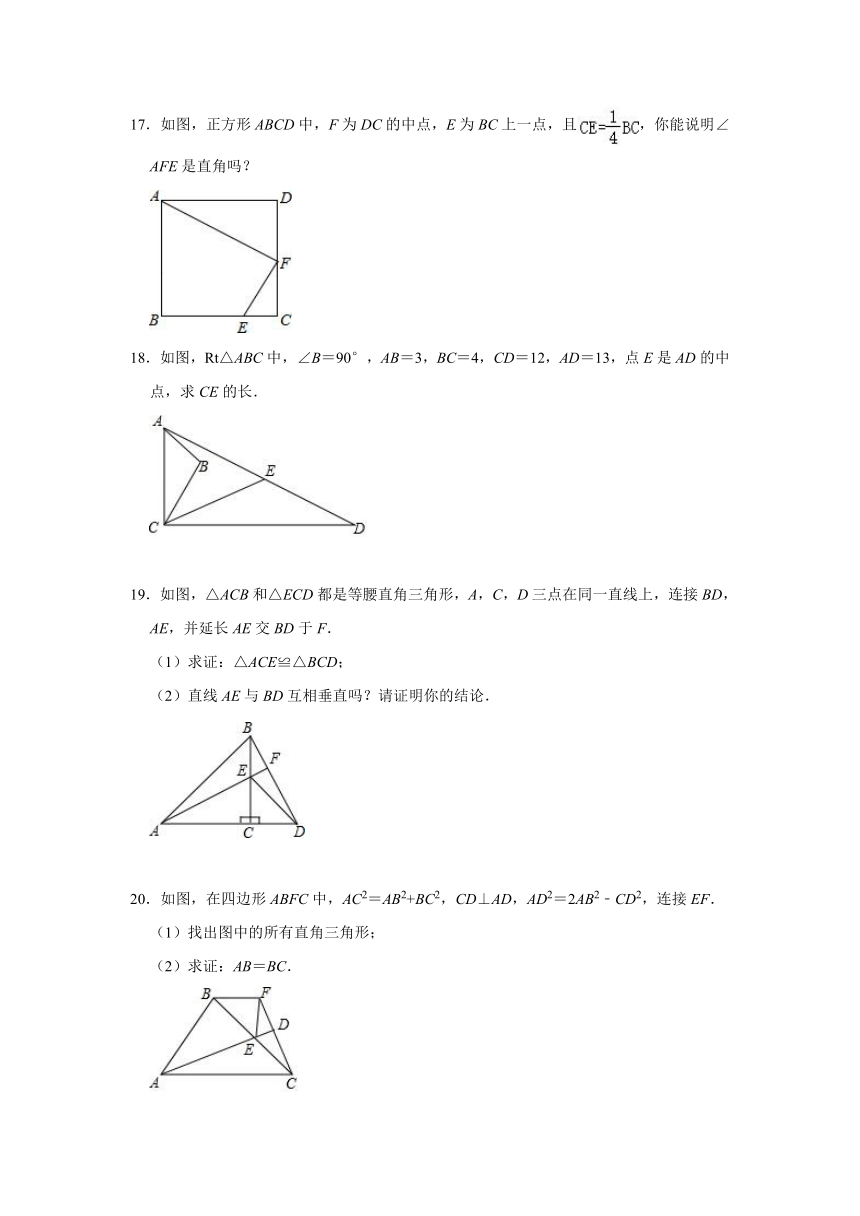
17.如图,正方形ABCD中,F为DC的中点,E为BC上一点,且,你能说明∠AFE是直角吗?
18.如图,Rt△ABC中,∠B=90°,AB=3,BC=4,CD=12,AD=13,点E是AD的中点,求CE的长.
19.如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.
20.如图,在四边形ABFC中,AC2=AB2+BC2,CD⊥AD,AD2=2AB2﹣CD2,连接EF.
(1)找出图中的所有直角三角形;
(2)求证:AB=BC.
21.如图,方格中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)△ABC的周长;
(2)请判断三角形ABC是否是直角三角形,并说明理由;
(3)△ABC的面积;
(4)点C到AB边的距离.
参考答案
1.解:A、∠A+∠B=∠C,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
B、∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
C、由a2=c2﹣b2,得a2+b2=c2,符合勾股定理的逆定理,是直角三角形;
D、32+42≠62,不符合勾股定理的逆定理,不是直角三角形.
故选:D.
2.解:∵(a﹣b)2+|a2+b2﹣c2|=0,
∴a﹣b=0,a2+b2﹣c2=0,
解得:a=b,a2+b2=c2,
∴△ABC的形状为等腰直角三角形;
故选:C.
3.解:A、∵1+2=3,∴不能构成三角形,故本选项错误;
B、∵22+32=13≠42,∴不能构成直角三角形,故本选项错误;
C、∵22+42=20≠52,∴不能构成直角三角形,故本选项错误;
D、∵32+42=25=52,∴能构成直角三角形,故本选项正确.
故选:D.
4.解:A、∵12+12≠22,∴不是勾股数,此选项错误;
B、1.5和2.5不是整数,此选项错误;
C、∵72+242=252,∴是勾股数,此选项正确;
D、∵62+122≠132,∴不是勾股数,此选项错误.
故选:C.
5.解:∵正方形小方格边长为1,
∴BC==2,
AC==,
AB==,
在△ABC中,
∵BC2+AC2=52+13=65,AB2=65,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
故选:A.
6.解:∵GH平分∠CGF,GI平分∠DGF,∠CGF+∠FGD=180°,
∴∠HGF+∠FGI=90°,
∵HG=15cm,GI=20cm,HI=25cm,
∴△HGI的边HI的高=,
即直线AB与直线CD之间的距离是12,
故选:B.
7.解:连接AC,
∵∠ABC=90°,AB=3,BC=4,
∴AC===5,
在△ACD中,AC2+CD2=25+144=169=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=AB?BC+AC?CD=×3×4+×5×12=36.
故答案为:36.
8.解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=3﹣t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=BP,
即t=(3﹣t),t=1(秒),
当∠BPQ=90°时,BP=BQ,
3﹣t=t,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
故答案为:1或2.
9.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
解得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×(9﹣3)×6=18(cm2).
故答案为:18.
10.解:AB2=22+22=8,
CD2=42+22=20,
EF2=12+22=5,
GH2=32+22=13,
所以AB2+EF2=GH2.
故其中能构成一个直角三角形三边的线段是AB,EF,GH.
故答案为:AB,EF,GH.
11.解:连接BC.
根据勾股定理可以得到:AB=BC=,AC=2,
∵()2+()2=(2)2,即AB2+BC2=AC2,
∴△ABC是等腰直角三角形.
∴∠BAC=45°.
故答案为:45°.
12.解:连接AC,在Rt△ACD中,AD=8,CD=6,
∴AC===10,
在△ABC中,
∵AC2+BC2=102+242=262=AB2,
∴△ABC为直角三角形;
∴图形面积为:
S△ABC﹣S△ACD=×10×24﹣×6×8=96.
故答案为:96.
13.解:∵三角形的两边长分别为1cm和2cm,
∴可设第三边为xcm,
∵此三角形是直角三角形,
∴当x是斜边时,x2=12+22,解得x=;
当x是直角边时,x2+12=22,解得x=.
故答案为:或.
14.解:(1)观察得给出的勾股数中,斜边与较大直角边的差是1,即c﹣b=1
∵a=19,a2+b2=c2,
∴192+b2=(b+1)2,
∴b=180,
∴c=181;
(2)通过观察知c﹣b=1,
∵(2n+1)2+b2=c2,
∴c2﹣b2=(2n+1)2,
(b+c)(c﹣b)=(2n+1)2,∴b+c=(2n+1)2,
又∵c=b+1,
∴2b+1=(2n+1)2,
∴b=2n2+2n,c=2n2+2n+1;
(3)由(2)知,2n+1,2n2+2n,2n2+2n+1为一组勾股数,
当n=7时,2n+1=15,112﹣111=1,
但2n2+2n=112≠111,
∴15,111,112不是一组勾股数.
故答案为:180,181.
15.证明:∵∠ABC=∠ACB,AC=3,
∴AB=AC=3,
又∵AD=5,BD=4,
∴AB2+BD2=25=AD2,
∴△ABD是直角三角形,且∠ABD=90°,
∴AB⊥BD.
16.解:(1)在△BCD中,BC=13,BD=12,CD=AC﹣AD=5,
∵52+122=169=132,即CD2+BD2=BC2,
∴∠BDC=90°.
在Rt△ABD中,AD=16,BD=12,∠ADB=90°,
∴AB==20.
又∵点E是边AB的中点,
∴DE=AB=10.
(2)当DE⊥AB时,DE长度最小.
此时:S△ABD=AD?BD=AB?DE,
∴DE==.
∴线段DE的最小值为.
17.解:连接AE,
设CE=a,则BC=4a,DF=2a,BE=3a,
AF2=AD2+DF2=20a2,EF2=FC2+EC2=5a2,AE2=AB2+BE2=25a2,
∵AE2=AF2+EF2
∴∠AFE是直角.
18.解:在Rt△ABC中,∠B=90°,
∵AB=3,BC=4,
∴,
∵CD=12,AD=13,
∵AC2+CD2=52+122=169,
AD2=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形,
∵点E是AD的中点,
∴CE=.
19.(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACE=∠BCD=90°,
在△ACE和△BCD,
∴△ACE≌△BCD(SAS);
(2)解:直线AE与BD互相垂直,理由为:
证明:∵△ACE≌△BCD,
∴∠EAC=∠DBC,
又∵∠DBC+∠CDB=90°,
∴∠EAC+∠CDB=90°,
∴∠AFD=90°,
∴AF⊥BD,
即直线AE与BD互相垂直.
20.解:(1)∵AC2=AB2+BC2,
∴△ABC是直角三角形,
∵CD⊥AD,
∴△ADC,△EDC,△EDF,△ABC,△ABE是直角三角形;
(2)∵AC2=AB2+BC2,AD2=2AB2﹣CD2,
∵△ADC是直角三角形,
∴AC2=AD2+DC2,
∴AB2+BC2=AD2+DC2,
∴AB2+BC2=2AB2﹣DC2+DC2
即AB2=BC2,
∴AB=BC.
21.解:(1)根据勾股定理知,BC==,AC==,AB==,
故△ABC的周长=AB+BC+AC=++;
(2)△ABC不是直角三角形,理由如下:
由(1)可知,BC=,AC=,AB=,AC<BC<AB,
∵AC2+BC2≠AB2,
∴△ABC不是直角三角形;
(3)如图,
S△ABC=S正方形BDEF﹣S△BCD﹣S△ACE﹣S△ABF
=3×3﹣×1×3﹣×1×2﹣×2×3
=;
(3)设点C到AB的距离是h.
由(3)知,三角形ABC的面积是,则AB?h=,即×h=,
解得,h=,即点C到AB的距离为.
暑假自学优生辅导训练(附答案)
1.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2 D.a:b:c=3:4:6
2.若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
3.下列四组线段中,能组成直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=2,b=4,c=5 D.a=3,b=4,c=5
4.下列各组数中,是勾股数的为( )
A.1,1,2 B.1.5,2,2.5 C.7,24,25 D.6,12,13
5.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.以上答案都不对
6.如图,直线AB∥CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是( )
A.10cm B.12cm C.13cm D.14cm
7.如图,已知四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=13,DA=12,则四边形ABCD的面积等于 .
8.已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止,当t= 时,△PBQ是直角三角形.
9.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为 cm2.
10.如图,在单位为1的正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是 .
11.如图,点A、B、C分别是正方体展开图的小正方形的顶点,则∠BAC的大小为 .
12.如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,该图形的面积等于 .
13.三角形的两边长分别为1cm和2cm,要使这个三角形是直角三角形,则第三条边长是 cm.
14.观察下列勾股数:
3,4,5;5,12,13;7,24,25;9,40,41;…:a,b,c.
根据你发现的规律,请写出:
(1)当a=19时,b= ,c= ;
(2)当a=2n+1时,求b、c的值;
(3)用(2)的结论判断15,111,112是否为一组勾股数,并说明理由.
15.如图,在△ABC中,∠ABC=∠ACB,AC=3,D是CA延长线上一点,AD=5,BD=4.求证:AB⊥BD.
16.如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长;
(2)若E是边AB上的动点,求线段DE的最小值.
17.如图,正方形ABCD中,F为DC的中点,E为BC上一点,且,你能说明∠AFE是直角吗?
18.如图,Rt△ABC中,∠B=90°,AB=3,BC=4,CD=12,AD=13,点E是AD的中点,求CE的长.
19.如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.
20.如图,在四边形ABFC中,AC2=AB2+BC2,CD⊥AD,AD2=2AB2﹣CD2,连接EF.
(1)找出图中的所有直角三角形;
(2)求证:AB=BC.
21.如图,方格中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)△ABC的周长;
(2)请判断三角形ABC是否是直角三角形,并说明理由;
(3)△ABC的面积;
(4)点C到AB边的距离.
参考答案
1.解:A、∠A+∠B=∠C,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
B、∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
C、由a2=c2﹣b2,得a2+b2=c2,符合勾股定理的逆定理,是直角三角形;
D、32+42≠62,不符合勾股定理的逆定理,不是直角三角形.
故选:D.
2.解:∵(a﹣b)2+|a2+b2﹣c2|=0,
∴a﹣b=0,a2+b2﹣c2=0,
解得:a=b,a2+b2=c2,
∴△ABC的形状为等腰直角三角形;
故选:C.
3.解:A、∵1+2=3,∴不能构成三角形,故本选项错误;
B、∵22+32=13≠42,∴不能构成直角三角形,故本选项错误;
C、∵22+42=20≠52,∴不能构成直角三角形,故本选项错误;
D、∵32+42=25=52,∴能构成直角三角形,故本选项正确.
故选:D.
4.解:A、∵12+12≠22,∴不是勾股数,此选项错误;
B、1.5和2.5不是整数,此选项错误;
C、∵72+242=252,∴是勾股数,此选项正确;
D、∵62+122≠132,∴不是勾股数,此选项错误.
故选:C.
5.解:∵正方形小方格边长为1,
∴BC==2,
AC==,
AB==,
在△ABC中,
∵BC2+AC2=52+13=65,AB2=65,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
故选:A.
6.解:∵GH平分∠CGF,GI平分∠DGF,∠CGF+∠FGD=180°,
∴∠HGF+∠FGI=90°,
∵HG=15cm,GI=20cm,HI=25cm,
∴△HGI的边HI的高=,
即直线AB与直线CD之间的距离是12,
故选:B.
7.解:连接AC,
∵∠ABC=90°,AB=3,BC=4,
∴AC===5,
在△ACD中,AC2+CD2=25+144=169=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=AB?BC+AC?CD=×3×4+×5×12=36.
故答案为:36.
8.解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=3﹣t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=BP,
即t=(3﹣t),t=1(秒),
当∠BPQ=90°时,BP=BQ,
3﹣t=t,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
故答案为:1或2.
9.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
解得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×(9﹣3)×6=18(cm2).
故答案为:18.
10.解:AB2=22+22=8,
CD2=42+22=20,
EF2=12+22=5,
GH2=32+22=13,
所以AB2+EF2=GH2.
故其中能构成一个直角三角形三边的线段是AB,EF,GH.
故答案为:AB,EF,GH.
11.解:连接BC.
根据勾股定理可以得到:AB=BC=,AC=2,
∵()2+()2=(2)2,即AB2+BC2=AC2,
∴△ABC是等腰直角三角形.
∴∠BAC=45°.
故答案为:45°.
12.解:连接AC,在Rt△ACD中,AD=8,CD=6,
∴AC===10,
在△ABC中,
∵AC2+BC2=102+242=262=AB2,
∴△ABC为直角三角形;
∴图形面积为:
S△ABC﹣S△ACD=×10×24﹣×6×8=96.
故答案为:96.
13.解:∵三角形的两边长分别为1cm和2cm,
∴可设第三边为xcm,
∵此三角形是直角三角形,
∴当x是斜边时,x2=12+22,解得x=;
当x是直角边时,x2+12=22,解得x=.
故答案为:或.
14.解:(1)观察得给出的勾股数中,斜边与较大直角边的差是1,即c﹣b=1
∵a=19,a2+b2=c2,
∴192+b2=(b+1)2,
∴b=180,
∴c=181;
(2)通过观察知c﹣b=1,
∵(2n+1)2+b2=c2,
∴c2﹣b2=(2n+1)2,
(b+c)(c﹣b)=(2n+1)2,∴b+c=(2n+1)2,
又∵c=b+1,
∴2b+1=(2n+1)2,
∴b=2n2+2n,c=2n2+2n+1;
(3)由(2)知,2n+1,2n2+2n,2n2+2n+1为一组勾股数,
当n=7时,2n+1=15,112﹣111=1,
但2n2+2n=112≠111,
∴15,111,112不是一组勾股数.
故答案为:180,181.
15.证明:∵∠ABC=∠ACB,AC=3,
∴AB=AC=3,
又∵AD=5,BD=4,
∴AB2+BD2=25=AD2,
∴△ABD是直角三角形,且∠ABD=90°,
∴AB⊥BD.
16.解:(1)在△BCD中,BC=13,BD=12,CD=AC﹣AD=5,
∵52+122=169=132,即CD2+BD2=BC2,
∴∠BDC=90°.
在Rt△ABD中,AD=16,BD=12,∠ADB=90°,
∴AB==20.
又∵点E是边AB的中点,
∴DE=AB=10.
(2)当DE⊥AB时,DE长度最小.
此时:S△ABD=AD?BD=AB?DE,
∴DE==.
∴线段DE的最小值为.
17.解:连接AE,
设CE=a,则BC=4a,DF=2a,BE=3a,
AF2=AD2+DF2=20a2,EF2=FC2+EC2=5a2,AE2=AB2+BE2=25a2,
∵AE2=AF2+EF2
∴∠AFE是直角.
18.解:在Rt△ABC中,∠B=90°,
∵AB=3,BC=4,
∴,
∵CD=12,AD=13,
∵AC2+CD2=52+122=169,
AD2=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形,
∵点E是AD的中点,
∴CE=.
19.(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACE=∠BCD=90°,
在△ACE和△BCD,
∴△ACE≌△BCD(SAS);
(2)解:直线AE与BD互相垂直,理由为:
证明:∵△ACE≌△BCD,
∴∠EAC=∠DBC,
又∵∠DBC+∠CDB=90°,
∴∠EAC+∠CDB=90°,
∴∠AFD=90°,
∴AF⊥BD,
即直线AE与BD互相垂直.
20.解:(1)∵AC2=AB2+BC2,
∴△ABC是直角三角形,
∵CD⊥AD,
∴△ADC,△EDC,△EDF,△ABC,△ABE是直角三角形;
(2)∵AC2=AB2+BC2,AD2=2AB2﹣CD2,
∵△ADC是直角三角形,
∴AC2=AD2+DC2,
∴AB2+BC2=AD2+DC2,
∴AB2+BC2=2AB2﹣DC2+DC2
即AB2=BC2,
∴AB=BC.
21.解:(1)根据勾股定理知,BC==,AC==,AB==,
故△ABC的周长=AB+BC+AC=++;
(2)△ABC不是直角三角形,理由如下:
由(1)可知,BC=,AC=,AB=,AC<BC<AB,
∵AC2+BC2≠AB2,
∴△ABC不是直角三角形;
(3)如图,
S△ABC=S正方形BDEF﹣S△BCD﹣S△ACE﹣S△ABF
=3×3﹣×1×3﹣×1×2﹣×2×3
=;
(3)设点C到AB的距离是h.
由(3)知,三角形ABC的面积是,则AB?h=,即×h=,
解得,h=,即点C到AB的距离为.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
