2021年暑假自学八年级数学 北师大版上册 《1.1探索勾股定理》优生辅导训练(word版含答案)
文档属性
| 名称 | 2021年暑假自学八年级数学 北师大版上册 《1.1探索勾股定理》优生辅导训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 744.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 01:05:54 | ||
图片预览

文档简介
2021年北师大版八年级数学上册《1.1探索勾股定理》暑假自学优生辅导训练(附答案)
1.在中,是直线上一点,已知,,,,则的长为( )
A.4或14 B.10或14 C.14 D.10
2.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )
A.8 B.10 C.12 D.14
3.如图,四边形ABCD中,AC⊥BD于O,AB=3,BC=4,CD=5,则AD的长为( )
A.1 B.3 C.4 D.2
4.在△ABC中,∠C=90°,若AB=5,则AB2+AC2+BC2=( )
A.10 B.15 C.30 D.50
5.在直角三角形中,自两锐角所引的两条中线长分别为5和2,则斜边长为( )
A.10 B.4 C. D.2
6.如图,矩形中,,,折叠纸片使点落在边上的处,折痕为,则的长为( )
A. B.2 C. D.1
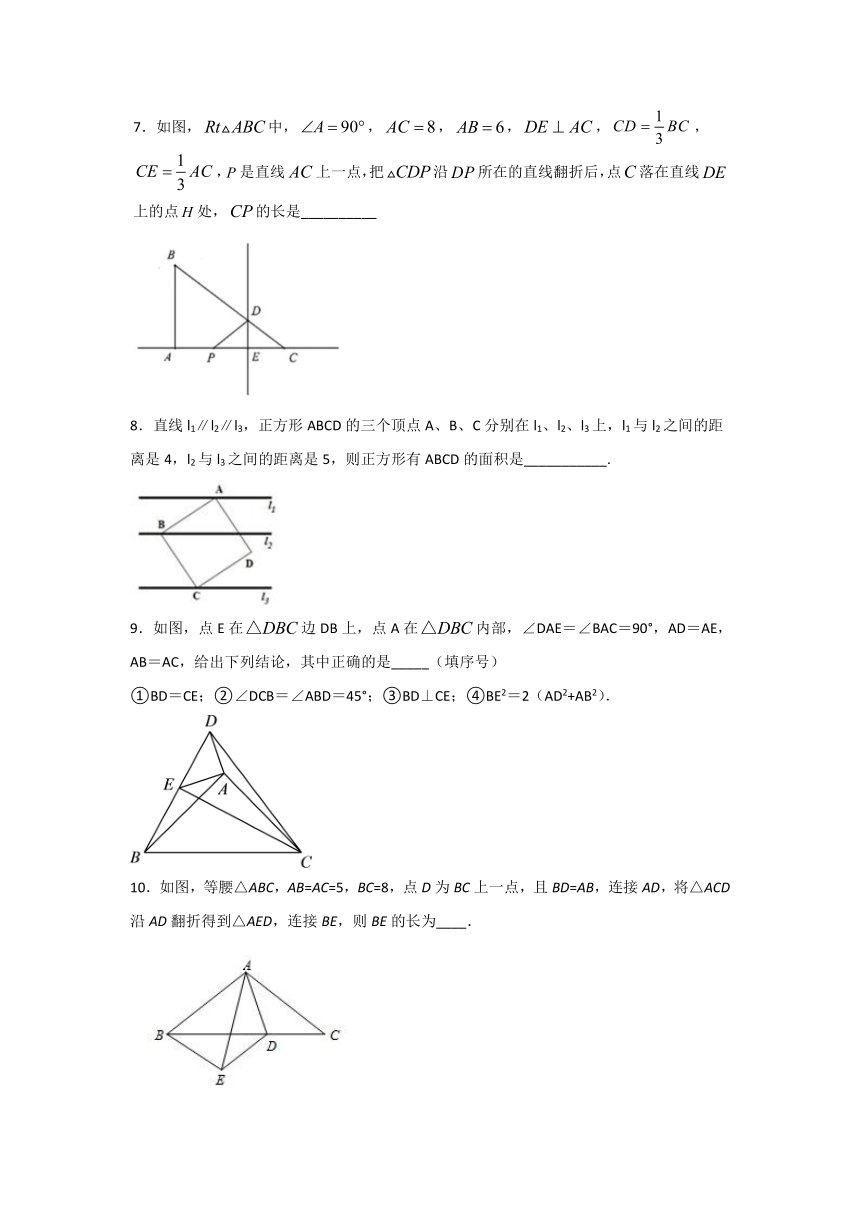
7.如图,中,,,,,,,是直线上一点,把沿所在的直线翻折后,点落在直线上的点处,的长是__________
8.直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2、l3上,l1与l2之间的距离是4,l2与l3之间的距离是5,则正方形有ABCD的面积是___________.
9.如图,点E在边DB上,点A在内部,∠DAE=∠BAC=90°,AD=AE,AB=AC,给出下列结论,其中正确的是_____(填序号)
①BD=CE;②∠DCB=∠ABD=45°;③BD⊥CE;④BE2=2(AD2+AB2).
10.如图,等腰△ABC,AB=AC=5,BC=8,点D为BC上一点,且BD=AB,连接AD,将△ACD沿AD翻折得到△AED,连接BE,则BE的长为____.
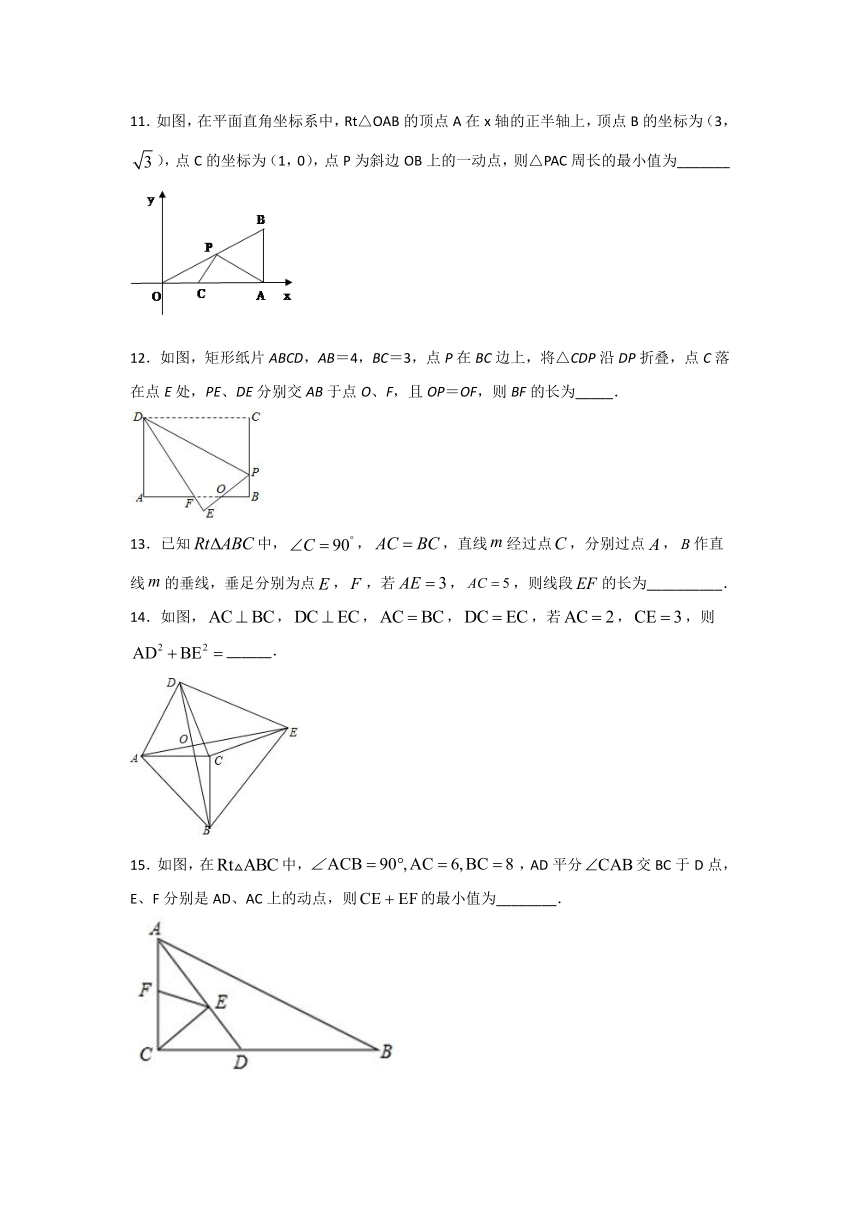
11.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(1,0),点P为斜边OB上的一动点,则△PAC周长的最小值为_______
12.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
13.已知中,,,直线经过点,分别过点,作直线的垂线,垂足分别为点,,若,,则线段的长为__________.
14.如图,,,,,若,,则______.
15.如图,在中,,AD平分交BC于D点,E、F分别是AD、AC上的动点,则的最小值为________.
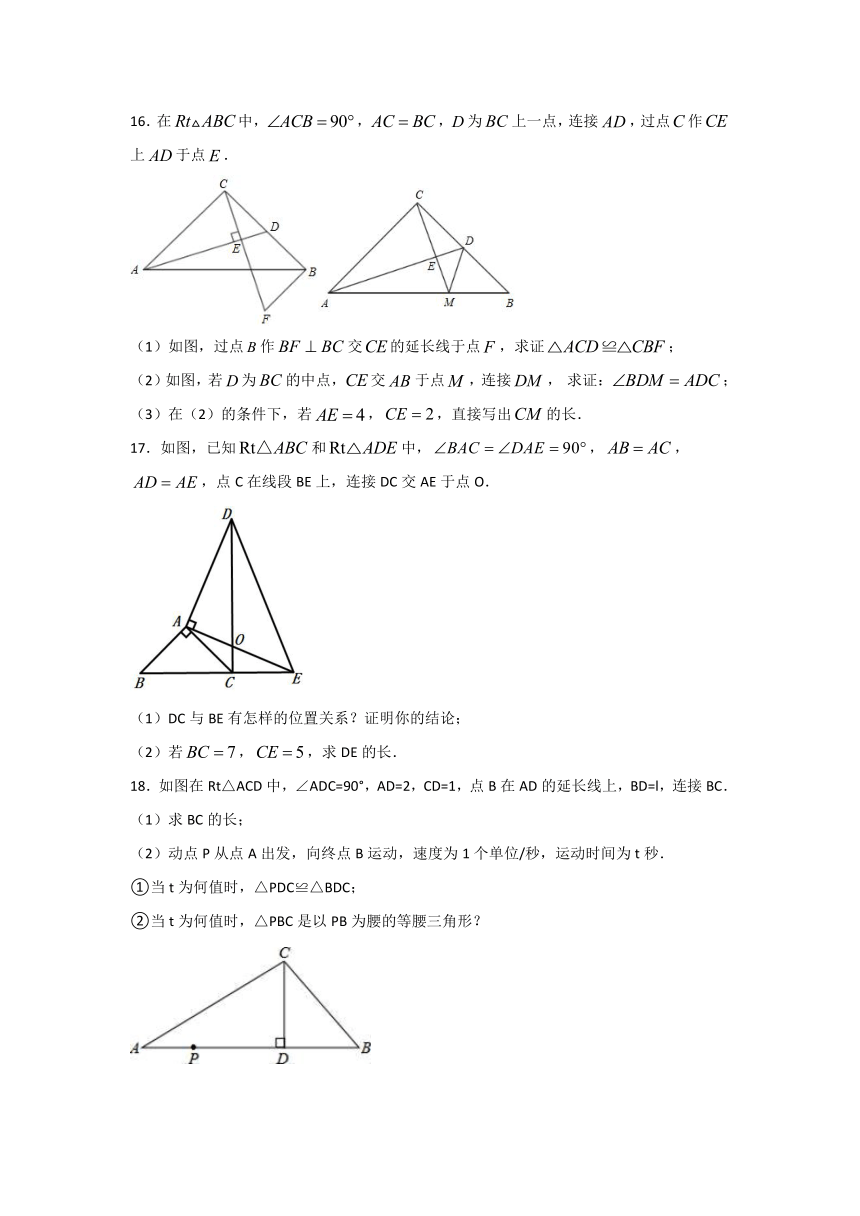
16.在中,,,为上一点,连接,过点作上于点.
(1)如图,过点作交的延长线于点,求证;
(2)如图,若为的中点,交于点,连接, 求证:;
(3)在(2)的条件下,若,,直接写出的长.
17.如图,已知和中,,,,点C在线段BE上,连接DC交AE于点O.
(1)DC与BE有怎样的位置关系?证明你的结论;
(2)若,,求DE的长.
18.如图在Rt△ACD中,∠ADC=90°,AD=2,CD=1,点B在AD的延长线上,BD=l,连接BC.
(1)求BC的长;
(2)动点P从点A出发,向终点B运动,速度为1个单位/秒,运动时间为t秒.
①当t为何值时,△PDC≌△BDC;
②当t为何值时,△PBC是以PB为腰的等腰三角形?
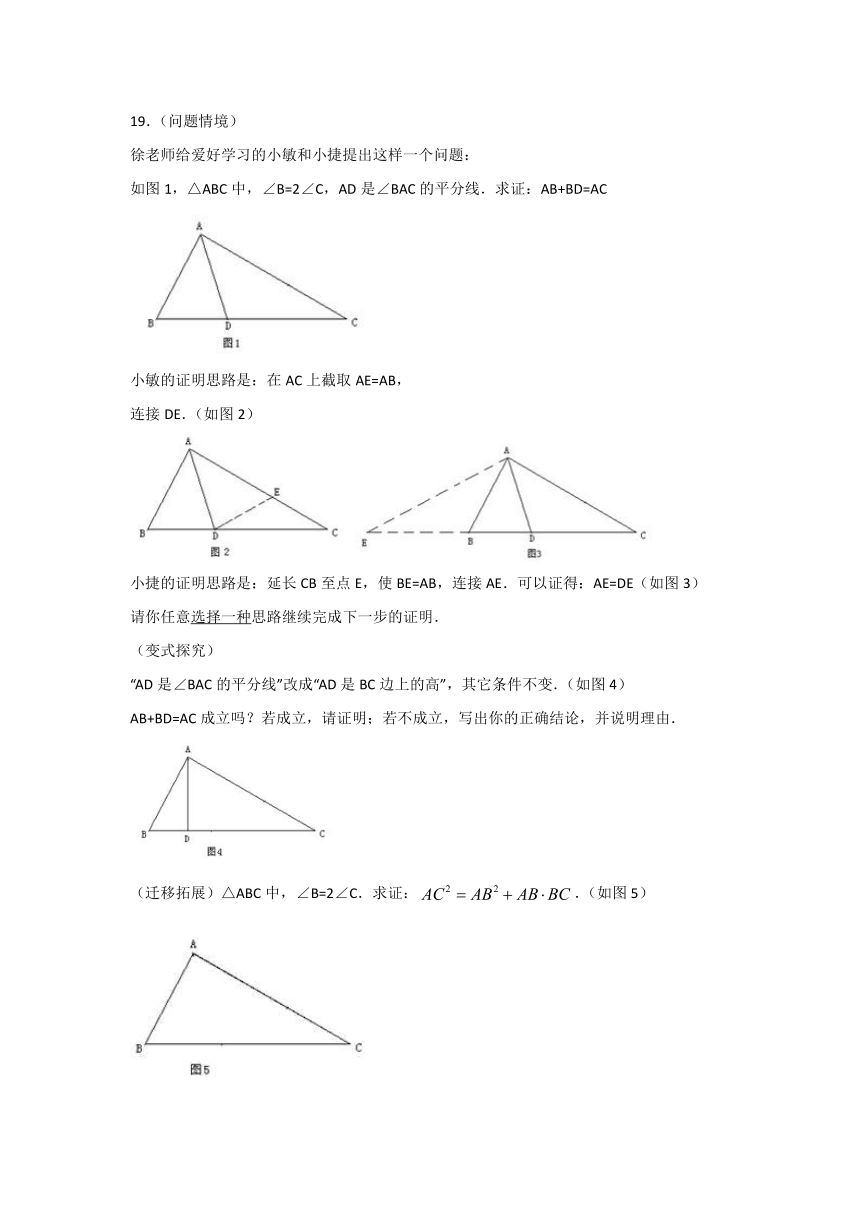
19.(问题情境)
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
小敏的证明思路是:在AC上截取AE=AB,
连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)
请你任意选择一种思路继续完成下一步的证明.
(变式探究)
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4)
AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.
(迁移拓展)△ABC中,∠B=2∠C.求证:.(如图5)
20.如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.
(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8.求AB的长度和DE的长度.
21.如图,在矩形ABCD中,AB=8,BC=10,E为CD边上一点,将△ADE沿AE折叠,使点D落在BC边上的点F处.
(1)求BF的长;
(2)求CE的长.
参考答案
题号 1 2 3 4 5 6
答案 A B B D D A
7.或
8.41
9.①③
10.
11.+2.
12.
13.或
14.26
15.
16.解:(1)证明:∵,,
∴,
∴,
∴,
又∵,
∴;
(2)证明:过点作交的延长线于点,如图所示:
由(1)得:,
∴,,
∵为的中点,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∴.
(3)解:连接,如图所示:
∵,,,
∴,
由(2)得:,,,
∴,,
∴,
∵,
∴是等腰直角三角形,
∴,
∴,
设,则,
在Rt△DEM中,由勾股定理得:,
解得:,
∴,
∴.
17.解:(1).
证明:
.
在和中,
.
(2)
,
.
.
18.解:(1)∵∠ADC=90°,CD=1,BD=l,
∴BC=;
(2)①∵△PDC≌△BDC,
∴PD=BD=1,即2-t=1,
解得t=1(秒);
②当P与点D重合时,
∵AD=2,
∴t=2秒;
当BP=BC时,
∵BC=,
∴BP=(AD+BD)-t=,即(2+1)-t=,解得t=(3-)秒.
故当t=2秒或t=(3-)秒时,△PBC是以PB为腰的等腰三角形.
19.解:小敏的证明思路是:在AC上截取AE=AB,连接DE.
由SAS证明△ABD≌△AED,得到BD=DE,∠ABD=∠AED,由∠AED=∠EDC+∠C和∠B=2∠C,得到∠EDC=∠C,从而有 DE=EC,故AB+BD=AC;
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE,则∠E=∠BAE,∠ABC=2∠E,由∠ABC=2∠C,得到∠E=∠C, AE=AC,再证△AED是等腰三角形,得到EA=ED=AC,故AB+BD=AC;
【变式探究】
AB+BD=AC不成立,正确结论:AB+BD=CD,在CD上截取DE=DB,由AD⊥BC,得到 AD是BE的中垂线,故AE=AB,∠B=∠AED,证明∠C=∠CAE,得到 AE=EC,即AB+BD=CD;
【迁移拓展】
过点A作AD⊥BC于D,由勾股定理得:,,故=(CD-BD)(CD+BD)=BC(CD-BD),由AB+BD="CD" ,得到 CD-BD=AB,
故= BC(CD-BD)=BC·AB,即.
试题解析:小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
∵AD是∠BAC的平分线,∴∠BAD=∠EAD,∵AD=AD,∴△ABD≌△AED,∴BD=DE,∠ABD=∠AED,又∵∠AED=∠EDC+∠C,∠B=2∠C,∴∠EDC=∠C,∴DE=EC,即AB+BD=AC;
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE,则∠E=∠BAE,∴∠ABC=2∠E,∵∠ABC=2∠C,∴∠E=∠C,∴AE=AC,∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE,又∵AD是∠BAC的平分线,∴∠BAD=∠DAC,∴∠ADE=∠DAE,∴△AED是等腰三角形,∴EA=ED=AC,∴AB+BD=AC;
【变式探究】
AB+BD=AC不成立 正确结论:AB+BD=CD,证明如下:
在CD上截取DE=DB,∵AD⊥BC,∴AD是BE的中垂线,∴AE=AB,∴∠B=∠AED,∵∠AED =∠C+∠CAE,∵∠B=2∠C,∴∠C=∠CAE,∴AE=EC,即AB+BD=CD;
【迁移拓展】
证明:过点A作AD⊥BC于D,由勾股定理得:,,∴=(CD-BD)(CD+BD)=BC(CD-BD),∵AB+BD="CD" ,∴CD-BD=AB,∴= BC(CD-BD)=BC·AB,即.
20.解:(1)∵∠C=90°,
∴∠CBP+∠BPC=90°,
∵DA⊥BA,
∴∠PBA+∠BDA=90°,
∵AD=AP,
∴∠BDA=∠DPA=∠BPC,
∴∠CBP=∠ABP;
(2)设AB=x,
∵AB?BC=4,
∴BC=x?4,
∵AC=8,
∴在Rt△ABC中,(x?4)2+64=x2,
解得:x=10,
即AB=10,
过点P作PF⊥BA于点F,如图
在△BCP和△BFP中:
∵
∴△BCP≌△BFP(AAS),
∴BF=BC=6,
∴AF=4,
∵DE⊥AC,
∴∠EAD+∠ADE=90°=∠PAF+∠EAD,
∴∠PAF=∠ADE,
在△PAF和△ADE中,
∴△PAF≌△ADE(AAS),
∴DE=AF=4.
21.解:(1)∵四边形ABCD为矩形,
∴∠B=90°,且AD=BC=10,
又∵AFE是由ADE沿AE翻折得到的,
∴AF=AD=10,
又∵AB=8,
在ABF中,由勾股定理得:,
故BF的长为6.
(2)设CE=x ,
∵四边形ABCD为矩形,
∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,
又∵△AFE是由△ADE沿AE翻折得到的,
∴FE=DE=8-x,
由(1)知:BF=6,故CF=BC-BF=10-6=4,
在CEF中,由勾股定理得:,
∴,解得:x=3,
故CE的长为3.
1.在中,是直线上一点,已知,,,,则的长为( )
A.4或14 B.10或14 C.14 D.10
2.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )
A.8 B.10 C.12 D.14
3.如图,四边形ABCD中,AC⊥BD于O,AB=3,BC=4,CD=5,则AD的长为( )
A.1 B.3 C.4 D.2
4.在△ABC中,∠C=90°,若AB=5,则AB2+AC2+BC2=( )
A.10 B.15 C.30 D.50
5.在直角三角形中,自两锐角所引的两条中线长分别为5和2,则斜边长为( )
A.10 B.4 C. D.2
6.如图,矩形中,,,折叠纸片使点落在边上的处,折痕为,则的长为( )
A. B.2 C. D.1
7.如图,中,,,,,,,是直线上一点,把沿所在的直线翻折后,点落在直线上的点处,的长是__________
8.直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2、l3上,l1与l2之间的距离是4,l2与l3之间的距离是5,则正方形有ABCD的面积是___________.
9.如图,点E在边DB上,点A在内部,∠DAE=∠BAC=90°,AD=AE,AB=AC,给出下列结论,其中正确的是_____(填序号)
①BD=CE;②∠DCB=∠ABD=45°;③BD⊥CE;④BE2=2(AD2+AB2).
10.如图,等腰△ABC,AB=AC=5,BC=8,点D为BC上一点,且BD=AB,连接AD,将△ACD沿AD翻折得到△AED,连接BE,则BE的长为____.
11.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(1,0),点P为斜边OB上的一动点,则△PAC周长的最小值为_______
12.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
13.已知中,,,直线经过点,分别过点,作直线的垂线,垂足分别为点,,若,,则线段的长为__________.
14.如图,,,,,若,,则______.
15.如图,在中,,AD平分交BC于D点,E、F分别是AD、AC上的动点,则的最小值为________.
16.在中,,,为上一点,连接,过点作上于点.
(1)如图,过点作交的延长线于点,求证;
(2)如图,若为的中点,交于点,连接, 求证:;
(3)在(2)的条件下,若,,直接写出的长.
17.如图,已知和中,,,,点C在线段BE上,连接DC交AE于点O.
(1)DC与BE有怎样的位置关系?证明你的结论;
(2)若,,求DE的长.
18.如图在Rt△ACD中,∠ADC=90°,AD=2,CD=1,点B在AD的延长线上,BD=l,连接BC.
(1)求BC的长;
(2)动点P从点A出发,向终点B运动,速度为1个单位/秒,运动时间为t秒.
①当t为何值时,△PDC≌△BDC;
②当t为何值时,△PBC是以PB为腰的等腰三角形?
19.(问题情境)
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
小敏的证明思路是:在AC上截取AE=AB,
连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)
请你任意选择一种思路继续完成下一步的证明.
(变式探究)
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4)
AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.
(迁移拓展)△ABC中,∠B=2∠C.求证:.(如图5)
20.如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.
(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8.求AB的长度和DE的长度.
21.如图,在矩形ABCD中,AB=8,BC=10,E为CD边上一点,将△ADE沿AE折叠,使点D落在BC边上的点F处.
(1)求BF的长;
(2)求CE的长.
参考答案
题号 1 2 3 4 5 6
答案 A B B D D A
7.或
8.41
9.①③
10.
11.+2.
12.
13.或
14.26
15.
16.解:(1)证明:∵,,
∴,
∴,
∴,
又∵,
∴;
(2)证明:过点作交的延长线于点,如图所示:
由(1)得:,
∴,,
∵为的中点,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∴.
(3)解:连接,如图所示:
∵,,,
∴,
由(2)得:,,,
∴,,
∴,
∵,
∴是等腰直角三角形,
∴,
∴,
设,则,
在Rt△DEM中,由勾股定理得:,
解得:,
∴,
∴.
17.解:(1).
证明:
.
在和中,
.
(2)
,
.
.
18.解:(1)∵∠ADC=90°,CD=1,BD=l,
∴BC=;
(2)①∵△PDC≌△BDC,
∴PD=BD=1,即2-t=1,
解得t=1(秒);
②当P与点D重合时,
∵AD=2,
∴t=2秒;
当BP=BC时,
∵BC=,
∴BP=(AD+BD)-t=,即(2+1)-t=,解得t=(3-)秒.
故当t=2秒或t=(3-)秒时,△PBC是以PB为腰的等腰三角形.
19.解:小敏的证明思路是:在AC上截取AE=AB,连接DE.
由SAS证明△ABD≌△AED,得到BD=DE,∠ABD=∠AED,由∠AED=∠EDC+∠C和∠B=2∠C,得到∠EDC=∠C,从而有 DE=EC,故AB+BD=AC;
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE,则∠E=∠BAE,∠ABC=2∠E,由∠ABC=2∠C,得到∠E=∠C, AE=AC,再证△AED是等腰三角形,得到EA=ED=AC,故AB+BD=AC;
【变式探究】
AB+BD=AC不成立,正确结论:AB+BD=CD,在CD上截取DE=DB,由AD⊥BC,得到 AD是BE的中垂线,故AE=AB,∠B=∠AED,证明∠C=∠CAE,得到 AE=EC,即AB+BD=CD;
【迁移拓展】
过点A作AD⊥BC于D,由勾股定理得:,,故=(CD-BD)(CD+BD)=BC(CD-BD),由AB+BD="CD" ,得到 CD-BD=AB,
故= BC(CD-BD)=BC·AB,即.
试题解析:小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
∵AD是∠BAC的平分线,∴∠BAD=∠EAD,∵AD=AD,∴△ABD≌△AED,∴BD=DE,∠ABD=∠AED,又∵∠AED=∠EDC+∠C,∠B=2∠C,∴∠EDC=∠C,∴DE=EC,即AB+BD=AC;
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE,则∠E=∠BAE,∴∠ABC=2∠E,∵∠ABC=2∠C,∴∠E=∠C,∴AE=AC,∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE,又∵AD是∠BAC的平分线,∴∠BAD=∠DAC,∴∠ADE=∠DAE,∴△AED是等腰三角形,∴EA=ED=AC,∴AB+BD=AC;
【变式探究】
AB+BD=AC不成立 正确结论:AB+BD=CD,证明如下:
在CD上截取DE=DB,∵AD⊥BC,∴AD是BE的中垂线,∴AE=AB,∴∠B=∠AED,∵∠AED =∠C+∠CAE,∵∠B=2∠C,∴∠C=∠CAE,∴AE=EC,即AB+BD=CD;
【迁移拓展】
证明:过点A作AD⊥BC于D,由勾股定理得:,,∴=(CD-BD)(CD+BD)=BC(CD-BD),∵AB+BD="CD" ,∴CD-BD=AB,∴= BC(CD-BD)=BC·AB,即.
20.解:(1)∵∠C=90°,
∴∠CBP+∠BPC=90°,
∵DA⊥BA,
∴∠PBA+∠BDA=90°,
∵AD=AP,
∴∠BDA=∠DPA=∠BPC,
∴∠CBP=∠ABP;
(2)设AB=x,
∵AB?BC=4,
∴BC=x?4,
∵AC=8,
∴在Rt△ABC中,(x?4)2+64=x2,
解得:x=10,
即AB=10,
过点P作PF⊥BA于点F,如图
在△BCP和△BFP中:
∵
∴△BCP≌△BFP(AAS),
∴BF=BC=6,
∴AF=4,
∵DE⊥AC,
∴∠EAD+∠ADE=90°=∠PAF+∠EAD,
∴∠PAF=∠ADE,
在△PAF和△ADE中,
∴△PAF≌△ADE(AAS),
∴DE=AF=4.
21.解:(1)∵四边形ABCD为矩形,
∴∠B=90°,且AD=BC=10,
又∵AFE是由ADE沿AE翻折得到的,
∴AF=AD=10,
又∵AB=8,
在ABF中,由勾股定理得:,
故BF的长为6.
(2)设CE=x ,
∵四边形ABCD为矩形,
∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,
又∵△AFE是由△ADE沿AE翻折得到的,
∴FE=DE=8-x,
由(1)知:BF=6,故CF=BC-BF=10-6=4,
在CEF中,由勾股定理得:,
∴,解得:x=3,
故CE的长为3.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
