2020--2021学年北师大版七年级数学下册第三章变量之间的关系复习课件(23张ppt)
文档属性
| 名称 | 2020--2021学年北师大版七年级数学下册第三章变量之间的关系复习课件(23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 678.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 10:38:08 | ||
图片预览






文档简介
(共23张PPT)
北师大版
七年级下
第三章
变量之间的关系复习
学习目标
1.掌握自变量、因变量、常量的概念,并理解因变量随着自变量的变化而变化
;
2.理解掌握变量之间的关系的三种表达方式。
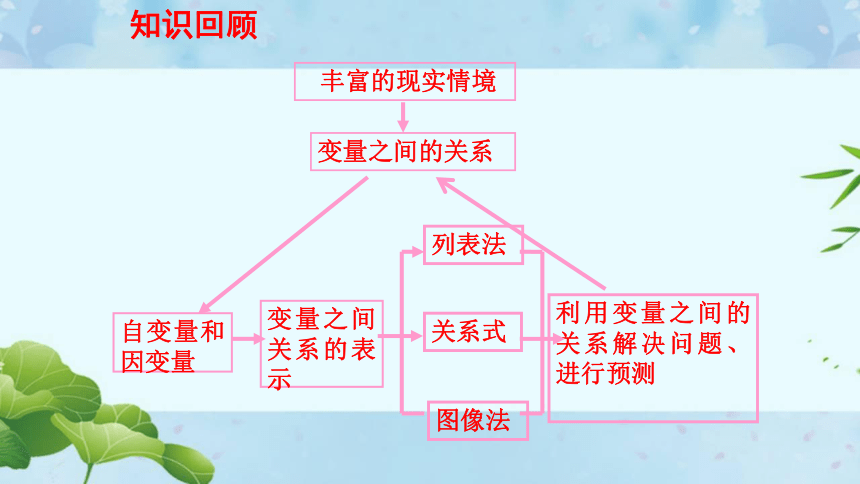
知识回顾
丰富的现实情境
自变量和因变量
变量之间关系的表示
列表法
关系式
图像法
利用变量之间的关系解决问题、进行预测
变量之间的关系
一.
表格法
1.借助表格可以感知因变量随自变量变化的情况。
2.从表格中可以获取一些信息,能作出某种预测或估计。
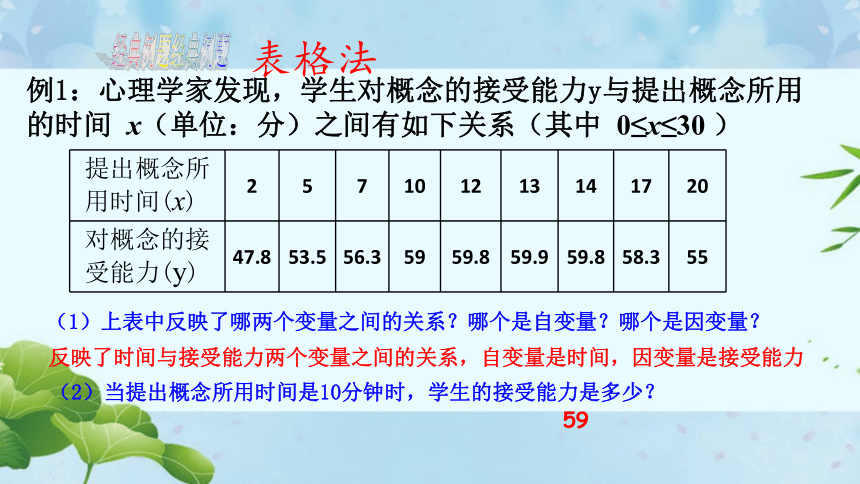
例1:心理学家发现,学生对概念的接受能力y与提出概念所用的时间
x(单位:分)之间有如下关系(其中
0≤x≤30
)
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少?
反映了时间与接受能力两个变量之间的关系,自变量是时间,因变量是接受能力
59
表格法
(4)从表格中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强?
(5)
根据表格大致估计当时间为23分钟时,学生对概念的接受能力是多少。
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
13分钟时,接受能力最强
0-13分钟时,接受能力逐步增强;13分钟以后,接受能力逐步降低;
约49
二.关系式法
1、借助关系式可以感知因变量随自变量变化的情况。
2、利用关系式进行计算求值。
关系式法
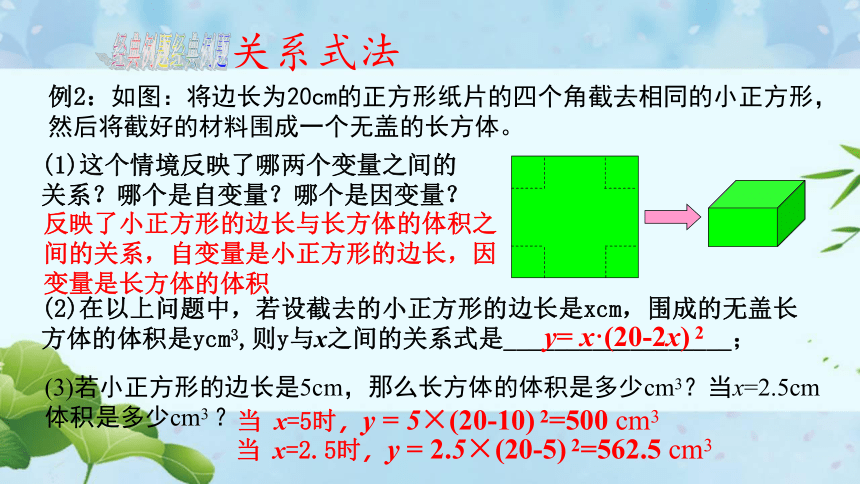
例2:如图:将边长为20cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体。
(2)在以上问题中,若设截去的小正方形的边长是xcm,围成的无盖长方体的体积是ycm3,则y与x之间的关系式是__________________;
(1)这个情境反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(3)若小正方形的边长是5cm,那么长方体的体积是多少cm3?当x=2.5cm体积是多少cm3
?
反映了小正方形的边长与长方体的体积之间的关系,自变量是小正方形的边长,因变量是长方体的体积
y=
x·(20-2x)
2
当
x=5时,y
=
5×(20-10)
2=500
cm3
当
x=2.5时,y
=
2.5×(20-5)
2=562.5
cm3
(4)根据以上关系式填下表:
x/cm
1
2
3
4
5
6
7
8
9
y/cm3
(5)当x在什么范围变化时,y随x的增大而增大,当x大约在什么范围变化时,y随x的增大而减小?
例2:如图:将边长为20cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体。
当x大于0小于3时,y随
x的增大而增大;当x大于3时,y随
x的增大而减小;
361
512
588
576
500
384
252
128
36
y=
x·(20-2x)
2
1.
用总长为60cm的铁丝围成长方形,如果长方形的一边长为
a(cm),面积为
S
(cm2)。
(1)说出这个变化中的自变量、因变量、常量。
(2)写出反映
a
与
S
之间的关系式。
(3)利用所写的关系式计算当a=12时,S的值是多少?
巩固练习
解:⑴
自变量是长a,因变量是面积
S
,常量是周长60
cm.
⑵
S=a·(30-a)
=
30a
-
a2
⑶
当a=12时,
S=30×12
-
122
=
360-144=216
2.果子成熟从树上落到地面,它落下的高度与经过的时间有如下的关系:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果果子经过2秒落到地上,那么请估计这果子开始落下时离地面的高度是多少米?
(3)请你列出果子落下的高度h(米)与时间t(秒)之间的关系式
.
时间t/秒
0.5
0.6
0.7
0.8
0.9
1
…
高度
h/米
5×0.25
5×0.36
5×0.49
5×0.64
5×0.81
5×1
…
巩固练习
反映了时间与高度两个变量之间的关系,
自变量是时间,因变量是高度。
5×22
=
20
(
米)
h=
5·t2
三.图像法
1、借助图像,分清因变量、自变量,并感知因变量随自变量变化的情况。
2、利用图像分析数据、变化趋势。
图像法
例3.小红与小兰从学校出发到距学校5千米的书店买书,下图反应了她们两人离开学校的路程与时间的关系。根据图形尝试解决你们提出的问题。
3
1
2
4
5
0
10
20
30
40
50
60
t/分钟
s/千米
实线---小兰
虚线---小红
(1)小红与小兰谁先出发?谁先到达?
(2)描述小兰离开学校的路程与时间
的变化关系。
小兰先出发,同时到达
当0s随t的增大而增大;
当20当50图像法
例3.小红与小兰从学校出发到距学校5千米的书店买书,下图反应了她们两人离开学校的路程与时间的关系。根据图形尝试解决你们提出的问题。
3
1
2
4
5
0
10
20
30
40
50
60
t/分钟
s/千米
实线---小兰
虚线---小红
(3)小兰前20分钟的速度和最后10分钟
的速度是多少?怎样从图像上直观地
反映速度的大小?
(4)小红与小兰从学校到书店的平均速度各是多少?
前20分钟的速度V=2÷20=0.1(千米/分)
后10分钟的速度V=(5-2)÷10=0.3(千米/分)
V小红=
5÷50=0.1(千米/分)
V小兰=
5÷60=
(千米/分)
1
12
巩固练习
1.
2012年6月份某一天沈阳的气温随时间变化的情况如图所示,回答下列问题:
(1)这天的最高气温约是
℃;
(2)
这天一共有
个小时的气温在24℃以上;
(3)这天在
范围内温度在上升;
这天在_______
范围内温度在下降;
温度/℃
20
22
24
26
28
时间
0
3
6
9
12
15
18
21
24
(4)请你预测一下,次日凌晨1点的气温大约多少度?
26
12
3-15时
0-3和15-24时
大约是21℃
当堂检测
时间
时间
速度
A
o
速度
D
速度
时间
C
速度
时间
B
o
o
o
2
.
汽车速度与行驶时间之间的关系可以用图象来表示
下图中A、B、C、D四个图象,可以分别用一句话来描述:
(1)在某段时间里,速度先越来越快接着越来
越慢(
)
(2)在某段时间里,汽车速度始终保持不变。(
)
(3)在某段时间里,汽车速度越来越快。
(
)
(4)在某段时间里,汽车速度越来越慢。(
)
A
C
B
D
当堂检测
3.
如果OA,BA分别表示甲、乙两名学生运动的路程s和时间t的关系,根图象判断快者的速度比慢者的速度每秒快(
)。
A.2.5m
B.2m
C.1.5m
D.1m
C
当堂检测
4.某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t
(1)
请完成下表
(2)汽车行驶5小时后,油箱中油量是
_____升?
(3)若汽车行驶过程中,油箱的油量为12升,则汽车行驶了
小时
;
汽车行驶时间t/小时
0
1
2.5
4
油箱的油量Q/升
60
(4)贮满60升汽油的汽车,最多行驶
____
小时;
54
45
36
30
8
10
当堂检测
5
如图是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系?(
)
(A)
(B)
(C)
(
D)
C
当堂检测
6.
如图:向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致是下列图象中的(
)
B
当堂检测
3.解图象信息题突出了数形结合的思想方法。
2.在图象中
上升线------表示因变量随自变量的增大而增大;
水平线-----表示因变量随自变量的增大而不变;
下降线------表示因变量随自变量的增大而减小。
以上三点是打开“解决图象类问题”的一把万能钥匙。
课堂小结
请按暂停键,想一想,有哪些收获
1.复习了表示变量关系的三种方法,表格法、关系式法、图像法,会确定自变量和因变量
作业布置
新课堂
本章综合测评题
P103-108
再
见
!
北师大版
七年级下
第三章
变量之间的关系复习
学习目标
1.掌握自变量、因变量、常量的概念,并理解因变量随着自变量的变化而变化
;
2.理解掌握变量之间的关系的三种表达方式。
知识回顾
丰富的现实情境
自变量和因变量
变量之间关系的表示
列表法
关系式
图像法
利用变量之间的关系解决问题、进行预测
变量之间的关系
一.
表格法
1.借助表格可以感知因变量随自变量变化的情况。
2.从表格中可以获取一些信息,能作出某种预测或估计。
例1:心理学家发现,学生对概念的接受能力y与提出概念所用的时间
x(单位:分)之间有如下关系(其中
0≤x≤30
)
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少?
反映了时间与接受能力两个变量之间的关系,自变量是时间,因变量是接受能力
59
表格法
(4)从表格中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强?
(5)
根据表格大致估计当时间为23分钟时,学生对概念的接受能力是多少。
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
13分钟时,接受能力最强
0-13分钟时,接受能力逐步增强;13分钟以后,接受能力逐步降低;
约49
二.关系式法
1、借助关系式可以感知因变量随自变量变化的情况。
2、利用关系式进行计算求值。
关系式法
例2:如图:将边长为20cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体。
(2)在以上问题中,若设截去的小正方形的边长是xcm,围成的无盖长方体的体积是ycm3,则y与x之间的关系式是__________________;
(1)这个情境反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(3)若小正方形的边长是5cm,那么长方体的体积是多少cm3?当x=2.5cm体积是多少cm3
?
反映了小正方形的边长与长方体的体积之间的关系,自变量是小正方形的边长,因变量是长方体的体积
y=
x·(20-2x)
2
当
x=5时,y
=
5×(20-10)
2=500
cm3
当
x=2.5时,y
=
2.5×(20-5)
2=562.5
cm3
(4)根据以上关系式填下表:
x/cm
1
2
3
4
5
6
7
8
9
y/cm3
(5)当x在什么范围变化时,y随x的增大而增大,当x大约在什么范围变化时,y随x的增大而减小?
例2:如图:将边长为20cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体。
当x大于0小于3时,y随
x的增大而增大;当x大于3时,y随
x的增大而减小;
361
512
588
576
500
384
252
128
36
y=
x·(20-2x)
2
1.
用总长为60cm的铁丝围成长方形,如果长方形的一边长为
a(cm),面积为
S
(cm2)。
(1)说出这个变化中的自变量、因变量、常量。
(2)写出反映
a
与
S
之间的关系式。
(3)利用所写的关系式计算当a=12时,S的值是多少?
巩固练习
解:⑴
自变量是长a,因变量是面积
S
,常量是周长60
cm.
⑵
S=a·(30-a)
=
30a
-
a2
⑶
当a=12时,
S=30×12
-
122
=
360-144=216
2.果子成熟从树上落到地面,它落下的高度与经过的时间有如下的关系:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果果子经过2秒落到地上,那么请估计这果子开始落下时离地面的高度是多少米?
(3)请你列出果子落下的高度h(米)与时间t(秒)之间的关系式
.
时间t/秒
0.5
0.6
0.7
0.8
0.9
1
…
高度
h/米
5×0.25
5×0.36
5×0.49
5×0.64
5×0.81
5×1
…
巩固练习
反映了时间与高度两个变量之间的关系,
自变量是时间,因变量是高度。
5×22
=
20
(
米)
h=
5·t2
三.图像法
1、借助图像,分清因变量、自变量,并感知因变量随自变量变化的情况。
2、利用图像分析数据、变化趋势。
图像法
例3.小红与小兰从学校出发到距学校5千米的书店买书,下图反应了她们两人离开学校的路程与时间的关系。根据图形尝试解决你们提出的问题。
3
1
2
4
5
0
10
20
30
40
50
60
t/分钟
s/千米
实线---小兰
虚线---小红
(1)小红与小兰谁先出发?谁先到达?
(2)描述小兰离开学校的路程与时间
的变化关系。
小兰先出发,同时到达
当0
当20
例3.小红与小兰从学校出发到距学校5千米的书店买书,下图反应了她们两人离开学校的路程与时间的关系。根据图形尝试解决你们提出的问题。
3
1
2
4
5
0
10
20
30
40
50
60
t/分钟
s/千米
实线---小兰
虚线---小红
(3)小兰前20分钟的速度和最后10分钟
的速度是多少?怎样从图像上直观地
反映速度的大小?
(4)小红与小兰从学校到书店的平均速度各是多少?
前20分钟的速度V=2÷20=0.1(千米/分)
后10分钟的速度V=(5-2)÷10=0.3(千米/分)
V小红=
5÷50=0.1(千米/分)
V小兰=
5÷60=
(千米/分)
1
12
巩固练习
1.
2012年6月份某一天沈阳的气温随时间变化的情况如图所示,回答下列问题:
(1)这天的最高气温约是
℃;
(2)
这天一共有
个小时的气温在24℃以上;
(3)这天在
范围内温度在上升;
这天在_______
范围内温度在下降;
温度/℃
20
22
24
26
28
时间
0
3
6
9
12
15
18
21
24
(4)请你预测一下,次日凌晨1点的气温大约多少度?
26
12
3-15时
0-3和15-24时
大约是21℃
当堂检测
时间
时间
速度
A
o
速度
D
速度
时间
C
速度
时间
B
o
o
o
2
.
汽车速度与行驶时间之间的关系可以用图象来表示
下图中A、B、C、D四个图象,可以分别用一句话来描述:
(1)在某段时间里,速度先越来越快接着越来
越慢(
)
(2)在某段时间里,汽车速度始终保持不变。(
)
(3)在某段时间里,汽车速度越来越快。
(
)
(4)在某段时间里,汽车速度越来越慢。(
)
A
C
B
D
当堂检测
3.
如果OA,BA分别表示甲、乙两名学生运动的路程s和时间t的关系,根图象判断快者的速度比慢者的速度每秒快(
)。
A.2.5m
B.2m
C.1.5m
D.1m
C
当堂检测
4.某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t
(1)
请完成下表
(2)汽车行驶5小时后,油箱中油量是
_____升?
(3)若汽车行驶过程中,油箱的油量为12升,则汽车行驶了
小时
;
汽车行驶时间t/小时
0
1
2.5
4
油箱的油量Q/升
60
(4)贮满60升汽油的汽车,最多行驶
____
小时;
54
45
36
30
8
10
当堂检测
5
如图是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系?(
)
(A)
(B)
(C)
(
D)
C
当堂检测
6.
如图:向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致是下列图象中的(
)
B
当堂检测
3.解图象信息题突出了数形结合的思想方法。
2.在图象中
上升线------表示因变量随自变量的增大而增大;
水平线-----表示因变量随自变量的增大而不变;
下降线------表示因变量随自变量的增大而减小。
以上三点是打开“解决图象类问题”的一把万能钥匙。
课堂小结
请按暂停键,想一想,有哪些收获
1.复习了表示变量关系的三种方法,表格法、关系式法、图像法,会确定自变量和因变量
作业布置
新课堂
本章综合测评题
P103-108
再
见
!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
