3.5.1 探索数字与图形规律 课件 2021—2022学年北师大版数学七年级上册(24张)
文档属性
| 名称 | 3.5.1 探索数字与图形规律 课件 2021—2022学年北师大版数学七年级上册(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 10:32:32 | ||
图片预览




文档简介
3.5.1 探索数字与图形规律
请同学们伸出左手,一起做下面的游戏:从大拇指开始,像图中显示的这只手那样依次数数字1,2,3,4,5,……,请问数字20落在哪个手指上?
你们能很快地说出数字200落在哪个手指上吗?2000呢?
情境导入
(1)请找出同一横行上三个相邻数、竖列上三个相邻数之间的关系:
同一横行上相邻三个数之间的关系:相差1.
竖列上三个相邻数的关系:相差7.
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
获取新知
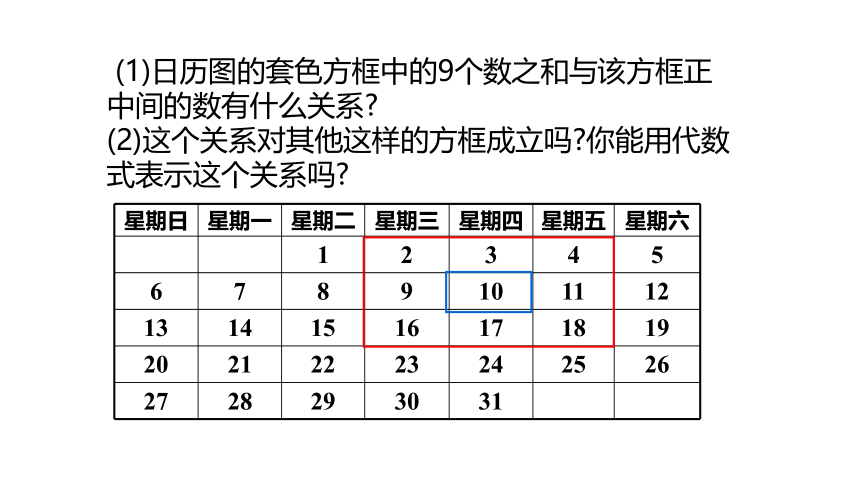
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?
(2)这个关系对其他这样的方框成立吗?你能用代数式表示这个关系吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
通过表格可以很快地解决方框中9个数之间的关系:9个数的和是中间这个数的9倍.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a-8
a-7
a-6
a-1
a
a+1
a+6
a+7
a+8
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)
+(a+7)+(a+8)= 9a.
答案
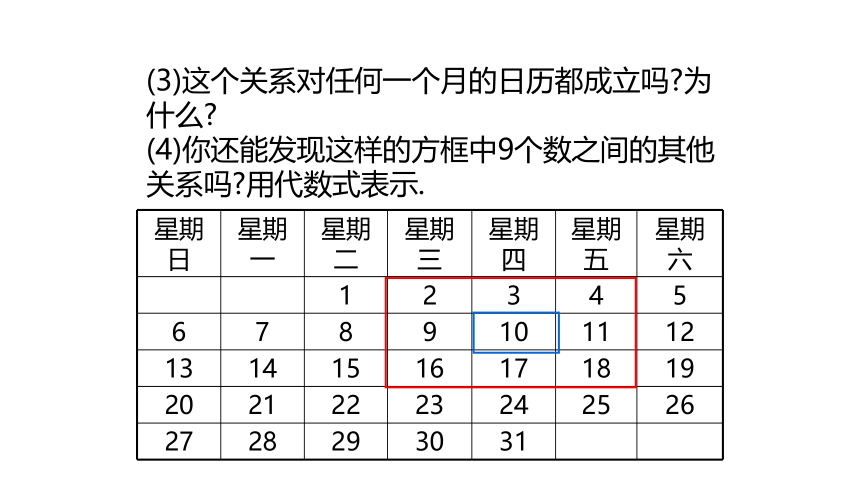
(3)这个关系对任何一个月的日历都成立吗?为什么?
(4)你还能发现这样的方框中9个数之间的其他关系吗?用代数式表示.
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
日历中的其他规律
(1)如果将方框改为十字形框,你能发现哪些规律?如果改为H形框呢?
“十”字形:5个数的和是中间这个数的5倍;
“H” 形:7个数的和是中间这个数的7倍;
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
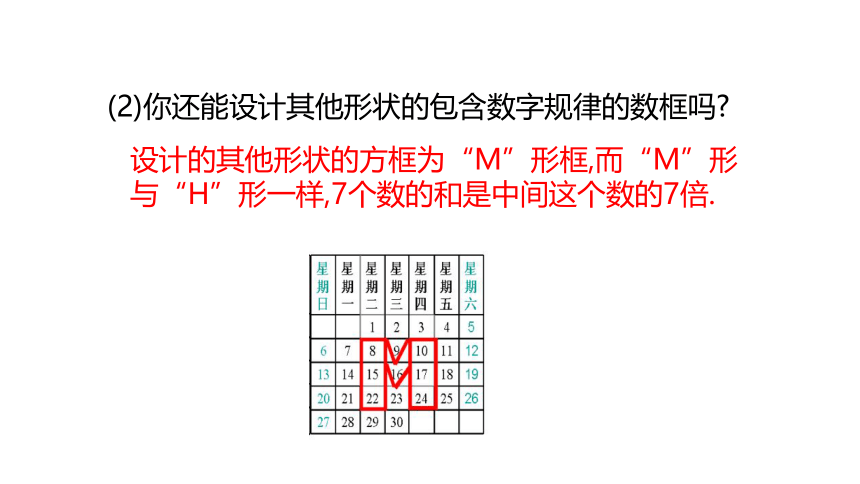
(2)你还能设计其他形状的包含数字规律的数框吗?
设计的其他形状的方框为“M”形框,而“M”形与“H”形一样,7个数的和是中间这个数的7倍.
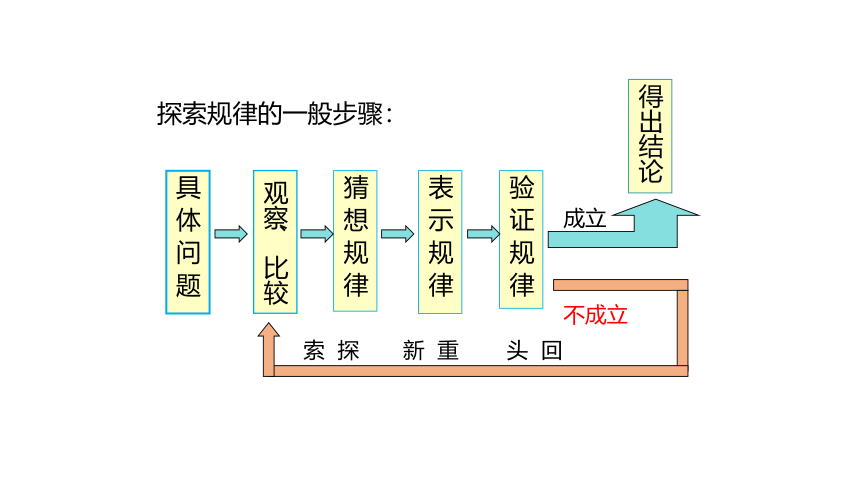
探索规律的一般步骤:
猜 想 规 律
表 示 规 律
验 证 规 律
具 体 问 题
观察、比较
成立
得出结论
不成立
头 回
新 重
索 探
观察下列等式,找出规律填空:
例题讲解
用代数式表示数的变化的规律:
(1)数字为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是奇、偶、平方等方面的规律;
(2)数字为分数,可分别观察分子、分母的变化规律及它们之间的联系;
(3)若表示数字变化规律的是等式(或表格),可将每个等式对应写好,然后比较每一行每一列数字之间的关系,从而找出规律.
正整数按下图的规律排列,则第20行,第21列的数字是________.
380
下面是用棋子摆成的“小屋子”,观察图形,回答问题.
(1)按图示规律填写下表:
(2)按这种方式摆下去,摆第n个这样的“小屋子”需要多少枚棋子?
图案编号
(1)
(2)
(3)
(4)
(5)
…
棋子个数
…
11
17
23
29
5
(6n-1)
以序号n为切入点
对于探索图形规律的题目,我们应该先观察图形排列顺序的规律, 然后把它们转化为相应的数据,并根据规律用代数式表示事物的数量关系以及它们的变化规律.
探索图形规律
C
随堂演练
2.如图30—1,第①个图形中共有1个小平行四边形,第②个图形中共有5个小平行四边形,第③个图形中共有11个小平行四边形……则第⑩个图形中小平行四边形的个数是( )
A.54 B.110
C.19 D.109
D
3.已知:(1)9×1+0=9;(2)9×2+1=19;(3)9×3+2=29;(4)9×4+3=39;….根据前面的式子构成的规律写出第(n)个式子是____________________(n是正整数).
9n+(n-1)=10n-1
4.观察图30-2中点的个数,若按其规律再画下去,可以得到第 个图形中所有点的个数为________(n是正整数).
(n+1)2
5.将棱长为1的正方体层层叠放如图所示,问第(5)个、第(6)个图形各需多少个正方体?
解:第(5)个图形需1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)=35(个)正方体.同理,第(6)个图形需56个正方体.
6. 如图是某月的日历,现用一方框在日历中任意框出四个数 ,请用一个等式表示a,b,c,d之间的关系
___________.(只要填一个即可)
a b
c d
a+d=b+c
课堂小结
请同学们伸出左手,一起做下面的游戏:从大拇指开始,像图中显示的这只手那样依次数数字1,2,3,4,5,……,请问数字20落在哪个手指上?
你们能很快地说出数字200落在哪个手指上吗?2000呢?
情境导入
(1)请找出同一横行上三个相邻数、竖列上三个相邻数之间的关系:
同一横行上相邻三个数之间的关系:相差1.
竖列上三个相邻数的关系:相差7.
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
获取新知
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?
(2)这个关系对其他这样的方框成立吗?你能用代数式表示这个关系吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
通过表格可以很快地解决方框中9个数之间的关系:9个数的和是中间这个数的9倍.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a-8
a-7
a-6
a-1
a
a+1
a+6
a+7
a+8
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)
+(a+7)+(a+8)= 9a.
答案
(3)这个关系对任何一个月的日历都成立吗?为什么?
(4)你还能发现这样的方框中9个数之间的其他关系吗?用代数式表示.
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
日历中的其他规律
(1)如果将方框改为十字形框,你能发现哪些规律?如果改为H形框呢?
“十”字形:5个数的和是中间这个数的5倍;
“H” 形:7个数的和是中间这个数的7倍;
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(2)你还能设计其他形状的包含数字规律的数框吗?
设计的其他形状的方框为“M”形框,而“M”形与“H”形一样,7个数的和是中间这个数的7倍.
探索规律的一般步骤:
猜 想 规 律
表 示 规 律
验 证 规 律
具 体 问 题
观察、比较
成立
得出结论
不成立
头 回
新 重
索 探
观察下列等式,找出规律填空:
例题讲解
用代数式表示数的变化的规律:
(1)数字为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是奇、偶、平方等方面的规律;
(2)数字为分数,可分别观察分子、分母的变化规律及它们之间的联系;
(3)若表示数字变化规律的是等式(或表格),可将每个等式对应写好,然后比较每一行每一列数字之间的关系,从而找出规律.
正整数按下图的规律排列,则第20行,第21列的数字是________.
380
下面是用棋子摆成的“小屋子”,观察图形,回答问题.
(1)按图示规律填写下表:
(2)按这种方式摆下去,摆第n个这样的“小屋子”需要多少枚棋子?
图案编号
(1)
(2)
(3)
(4)
(5)
…
棋子个数
…
11
17
23
29
5
(6n-1)
以序号n为切入点
对于探索图形规律的题目,我们应该先观察图形排列顺序的规律, 然后把它们转化为相应的数据,并根据规律用代数式表示事物的数量关系以及它们的变化规律.
探索图形规律
C
随堂演练
2.如图30—1,第①个图形中共有1个小平行四边形,第②个图形中共有5个小平行四边形,第③个图形中共有11个小平行四边形……则第⑩个图形中小平行四边形的个数是( )
A.54 B.110
C.19 D.109
D
3.已知:(1)9×1+0=9;(2)9×2+1=19;(3)9×3+2=29;(4)9×4+3=39;….根据前面的式子构成的规律写出第(n)个式子是____________________(n是正整数).
9n+(n-1)=10n-1
4.观察图30-2中点的个数,若按其规律再画下去,可以得到第 个图形中所有点的个数为________(n是正整数).
(n+1)2
5.将棱长为1的正方体层层叠放如图所示,问第(5)个、第(6)个图形各需多少个正方体?
解:第(5)个图形需1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)=35(个)正方体.同理,第(6)个图形需56个正方体.
6. 如图是某月的日历,现用一方框在日历中任意框出四个数 ,请用一个等式表示a,b,c,d之间的关系
___________.(只要填一个即可)
a b
c d
a+d=b+c
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
