5.6 应用一元一次方程---追赶小明 课件 2021—2022学年北师大版数学七年级上册(36张)
文档属性
| 名称 | 5.6 应用一元一次方程---追赶小明 课件 2021—2022学年北师大版数学七年级上册(36张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览








文档简介
5.6 应用一元一次方程——追赶小明
小明和小华相距10米,他们同时出发,相向而行,小明每秒走3米,小华每秒走4米,他们能相遇吗?几秒钟可以相遇?
等量关系:
小明走的路程+小华走的路程=相距的路程
所用公式:路程=速度×时间
情境导入
这道题是小学做过的一种很常见的应用题:行程问题,
用到的数量关系主要有:
路程=平均速度×时间;
时间=路程÷平均速度.
行程问题就是要抓住速度、路程、时间三个量之间的关系,找出等量关系,正确地列出方程,解决实际问题.
1.若杰瑞的速度是6米/秒,则它5秒跑了________米.
2.若汤姆的速度是7米/秒,要抓到14米远处正在吃食物而毫无防备的杰瑞需要________秒.
3.若杰瑞想在4秒钟内抢在汤姆前面吃到放在30米处的奶酪,则它至少每秒钟要跑________米.
30
2
7.25
小明每天早上要在7: 50之前赶到距家1 000 m的学校上学.一天,小明以80 m/min的速度出发,5 min后,小明的爸爸发现他忘了带语文书.于是, 爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
获取新知
分析:当爸爸追上小明时,两人所走路程相等.
解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x=180x.
答:爸爸追上小明用了4分钟.
(2)180×4=720(米),1000-720=280(米).
答:追上小明时,距离学校还有280米.
化简,得 100x=400. x=4.
80×5
80x
180x
在审题过程中,如果能把文字语言变成图形语言——线段图,即可使问题更加直观,等量关系更加清晰.我们只要设出未知数,并用代数式表示出来,便可以得到方程.
例1 小丽和小红每天早晨坚持跑步,小红每秒跑 4米,小丽每秒跑6米.
(1)如果她们从100米跑道的两端相向跑,那么几秒之后两人相遇?
(2)如果小丽站在百米跑道起跑处,小红站在她面前10米处,两人同时同向起跑,几秒后小丽追上小红?
例题讲解
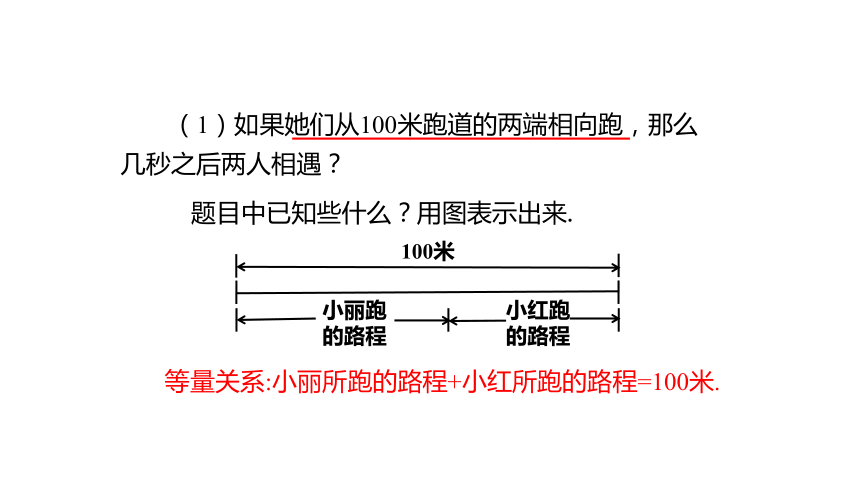
(1)如果她们从100米跑道的两端相向跑,那么几秒之后两人相遇?
题目中已知些什么?用图表示出来.
等量关系:小丽所跑的路程+小红所跑的路程=100米.
小丽跑的路程
小红跑的路程
100米
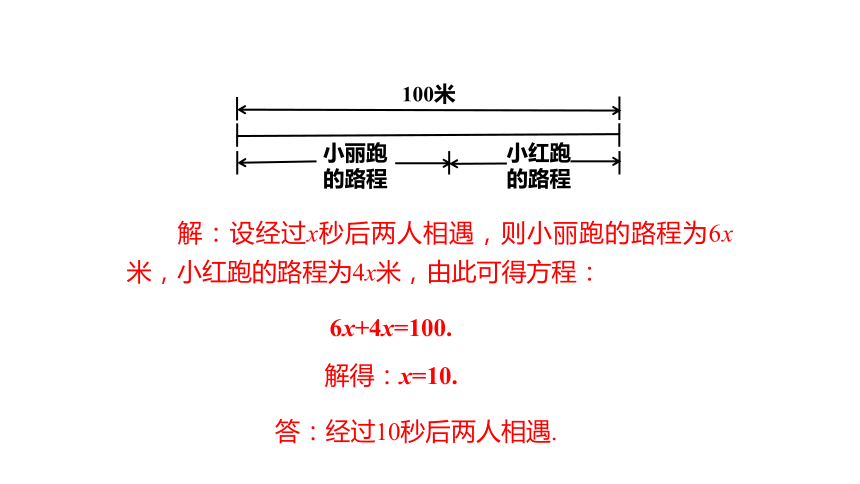
解:设经过x秒后两人相遇,则小丽跑的路程为6x米,小红跑的路程为4x米,由此可得方程:
6x+4x=100.
解得:x=10.
答:经过10秒后两人相遇.
小丽跑的路程
小红跑的路程
100米
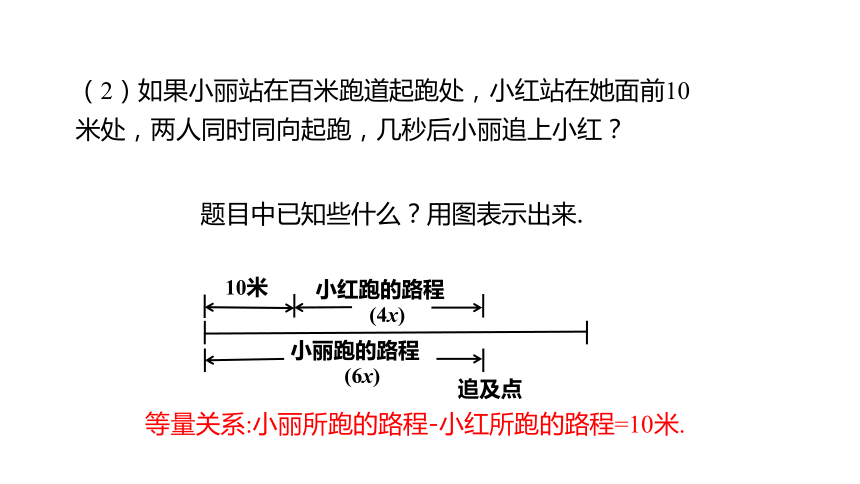
题目中已知些什么?用图表示出来.
(2)如果小丽站在百米跑道起跑处,小红站在她面前10米处,两人同时同向起跑,几秒后小丽追上小红?
小丽跑的路程
(6x)
小红跑的路程
(4x)
10米
追及点
等量关系:小丽所跑的路程-小红所跑的路程=10米.
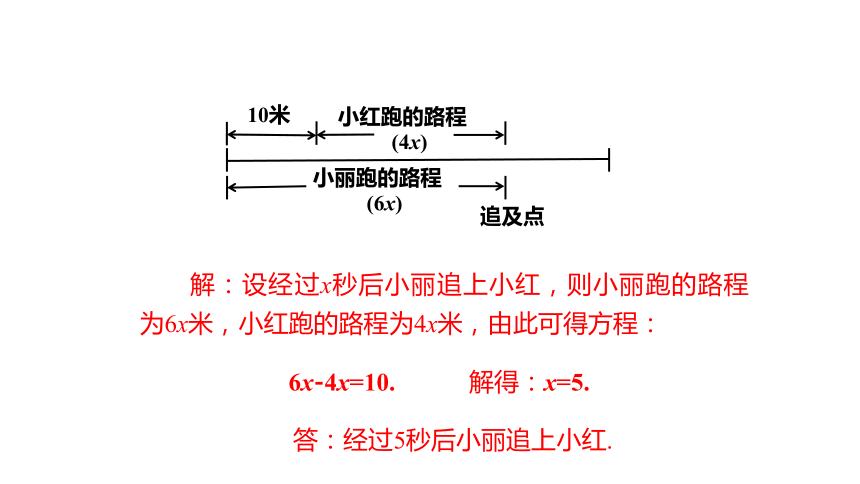
解:设经过x秒后小丽追上小红,则小丽跑的路程为6x米,小红跑的路程为4x米,由此可得方程:
6x-4x=10.
解得:x=5.
答:经过5秒后小丽追上小红.
小丽跑的路程
(6x)
小红跑的路程
(4x)
10米
追及点
相遇问题:
关于两人从两地出发相向而行的行程问题称为相遇问题,这
类问题往往根据路程之和等于总路程列方程.如图5-6-1所示,甲的行程+乙的行程=两地相距的路程.
图5-6-1
A,B两地相距60千米,甲、乙两人分别从A,B两地出发相向而行,甲的速度是8千米/时,乙的速度是6千米/时.经过多长时间两人相距4千米?
8x
6x
60
4
A
B
8x
6x
60
4
A
B
追及问题:
(1)对于同向同时不同地的问题,如图5-6-2所示,甲的行程-乙的行程=两出发地相距的路程;
图5-6-2
(2)对于同向同地不同时的问题,如图5-6-3所示,甲的
行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
一队学生去校外进行军事野营训练,他们以5 km/h的速度行进,走了18 min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14 km/h的速度按原路追上去,通讯员用多少时间可以追上学生的队伍?
相等关系:通讯员的行进路程=学生的行进路程.
5×18/60
5x
14x
注意单位统一
问题1:操场一周是400米,小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行,他俩能相遇吗?
环形跑道问题
分 析
小华
小明
同时同地同向而行
能相遇
问题2:操场一周是400米,小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
分 析
小华
小明
同时同地同向而行
拓展训练:
经过几秒钟两人第三次相遇?
解:设经过x秒两人第一次相遇,依题意,得
10x-5x=400,
解得x=80.
答:经过80秒两人第一次相遇
变式训练:操场一周是400米,小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行,两人同时同地相背而行,则两个人何时相遇?
分 析
小华
小明
同时同地
相背而行
解:设经过x秒两人第一次相遇,依题意,得
10x+5x=400,
解得x= .
答:经过 秒两人第一次相遇
环形跑道问题:设v甲>v乙,环形跑道长s米,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:
v甲t-v乙t=s.
①同时同地、背向而行:
v甲t+v乙t=s.
例2 小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步.小明跑2圈用的时间和他的哥哥跑3圈用的时间相等.两人同时同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
解:设小明的速度为x m/s,
则他的哥哥的速度为 x m/s,
由题意得160x=160× -400.
解得x=5.
则小明的哥哥的速度为5× =7.5(m/s).
设经过y s他们第一次相遇,
由题意,得(5+7.5)y=400.解得y=32.
答:经过32 s他们第一次相遇.
例2 顺(逆)水(风)问题一架飞机在两个城市之间飞行,当顺风飞行时需2.9 h,当逆风飞行时则需3.1 h.已知风速为20 km/h,求无风时飞机的航速和这两个城市之间的距离.
设无风时飞机的航速为x km/h,根据顺风速度=无风速度+风速,逆风速度=无风速度-风速,由路程=速度×时间列出方程,求出方程的解即可得到结果.
解:设无风时飞机的航速为x km/h,
根据题意,得2.9(x+20)=3.1(x-20).
解这个方程,得x=600.
则3.1(x-20)=1798.
因此,无风时飞机的航速为600 km/h,这两个城市之间的距离为1798 km.
1.顺(逆)风问题中的有关公式:
①顺风速度=无风速度+风速;②逆风速度=无风速度-风
速;③顺风速度-逆风速度=2×风速.
2.顺(逆)水问题中的有关公式:
①顺水速度=静水中的速度+水流速度;②逆水速度=静水
中的速度-水流速度;③顺水速度-逆水速度=2×水流速度.
例3家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
①他下山时的速度比上山时的速度每小时快1 km;
②他上山2 h到达的位置,离山顶还有1 km;
③抄近路下山,下山路程比上山路程近2 km;
④下山用1 h.
根据上面信息,他做出如下计划:
(1)在山顶游览1 h;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,
请问:孔明同学应该在什么时间从家出发?
解:设上山的速度为v km/h,
则下山的速度为(v+1) km/h,
由题意得2v+1=v+1+2,解得v=2.
即上山速度是2 km/h.
A
随堂演练
2.甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒跑6米,甲每秒跑8米.如果甲在乙前面8米处同时同向出发,那么经过几秒两人首次相遇( )
A.208秒 B.204秒
C.200秒 D.196秒
D
3.甲、乙两人赛跑,甲的速度是8米/秒,乙的速度是5米/秒,如果甲从起点处往后退20米,乙从起点处向前进10米,若甲、乙两人同时出发,则甲经过几秒钟追上乙?
解:设甲经过x秒追上乙.由题意,得8x-5x=20+10.解这个方程,得x=10.
因此,甲经过10秒追上乙.
4.A,B两地相距30千米.甲、乙两人分别从A,B两地同时出发,相向而行.已知甲比乙每小时多走1千米,经过2.5小时两人相遇,求甲、乙两人的速度.
解:设乙的速度为x千米/时,则甲的速度为(x+1)千米/时.
根据题意,得2.5x+2.5(x+1)=30.
解这个方程,得x=5.5.则x+1=6.5.
因此,甲、乙两人的速度分别为6.5千米/时、5.5千米/时.
5.甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
(2)若两车同时开出,相背而行,多少小时后两车相距1 800 km?
(3)若两车同时开出,快车在慢车后面同向而行,多少小时后两车相距1 200 km(此时快车在慢车的后面)?
解:(1)设快车开出x h后两车相遇.
由题意,得60× +90x=1 500,
解得x=9.8.
答:快车开出9.8 h后两车相遇.
(2)设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800,
解得y=2.
答:2 h后两车相距1 800 km.
(3)设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200,
解得z=10.
答:10 h后两车相距1 200 km(此时快车在慢车的
后面).
课堂小结
小明和小华相距10米,他们同时出发,相向而行,小明每秒走3米,小华每秒走4米,他们能相遇吗?几秒钟可以相遇?
等量关系:
小明走的路程+小华走的路程=相距的路程
所用公式:路程=速度×时间
情境导入
这道题是小学做过的一种很常见的应用题:行程问题,
用到的数量关系主要有:
路程=平均速度×时间;
时间=路程÷平均速度.
行程问题就是要抓住速度、路程、时间三个量之间的关系,找出等量关系,正确地列出方程,解决实际问题.
1.若杰瑞的速度是6米/秒,则它5秒跑了________米.
2.若汤姆的速度是7米/秒,要抓到14米远处正在吃食物而毫无防备的杰瑞需要________秒.
3.若杰瑞想在4秒钟内抢在汤姆前面吃到放在30米处的奶酪,则它至少每秒钟要跑________米.
30
2
7.25
小明每天早上要在7: 50之前赶到距家1 000 m的学校上学.一天,小明以80 m/min的速度出发,5 min后,小明的爸爸发现他忘了带语文书.于是, 爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
获取新知
分析:当爸爸追上小明时,两人所走路程相等.
解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x=180x.
答:爸爸追上小明用了4分钟.
(2)180×4=720(米),1000-720=280(米).
答:追上小明时,距离学校还有280米.
化简,得 100x=400. x=4.
80×5
80x
180x
在审题过程中,如果能把文字语言变成图形语言——线段图,即可使问题更加直观,等量关系更加清晰.我们只要设出未知数,并用代数式表示出来,便可以得到方程.
例1 小丽和小红每天早晨坚持跑步,小红每秒跑 4米,小丽每秒跑6米.
(1)如果她们从100米跑道的两端相向跑,那么几秒之后两人相遇?
(2)如果小丽站在百米跑道起跑处,小红站在她面前10米处,两人同时同向起跑,几秒后小丽追上小红?
例题讲解
(1)如果她们从100米跑道的两端相向跑,那么几秒之后两人相遇?
题目中已知些什么?用图表示出来.
等量关系:小丽所跑的路程+小红所跑的路程=100米.
小丽跑的路程
小红跑的路程
100米
解:设经过x秒后两人相遇,则小丽跑的路程为6x米,小红跑的路程为4x米,由此可得方程:
6x+4x=100.
解得:x=10.
答:经过10秒后两人相遇.
小丽跑的路程
小红跑的路程
100米
题目中已知些什么?用图表示出来.
(2)如果小丽站在百米跑道起跑处,小红站在她面前10米处,两人同时同向起跑,几秒后小丽追上小红?
小丽跑的路程
(6x)
小红跑的路程
(4x)
10米
追及点
等量关系:小丽所跑的路程-小红所跑的路程=10米.
解:设经过x秒后小丽追上小红,则小丽跑的路程为6x米,小红跑的路程为4x米,由此可得方程:
6x-4x=10.
解得:x=5.
答:经过5秒后小丽追上小红.
小丽跑的路程
(6x)
小红跑的路程
(4x)
10米
追及点
相遇问题:
关于两人从两地出发相向而行的行程问题称为相遇问题,这
类问题往往根据路程之和等于总路程列方程.如图5-6-1所示,甲的行程+乙的行程=两地相距的路程.
图5-6-1
A,B两地相距60千米,甲、乙两人分别从A,B两地出发相向而行,甲的速度是8千米/时,乙的速度是6千米/时.经过多长时间两人相距4千米?
8x
6x
60
4
A
B
8x
6x
60
4
A
B
追及问题:
(1)对于同向同时不同地的问题,如图5-6-2所示,甲的行程-乙的行程=两出发地相距的路程;
图5-6-2
(2)对于同向同地不同时的问题,如图5-6-3所示,甲的
行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
一队学生去校外进行军事野营训练,他们以5 km/h的速度行进,走了18 min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14 km/h的速度按原路追上去,通讯员用多少时间可以追上学生的队伍?
相等关系:通讯员的行进路程=学生的行进路程.
5×18/60
5x
14x
注意单位统一
问题1:操场一周是400米,小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行,他俩能相遇吗?
环形跑道问题
分 析
小华
小明
同时同地同向而行
能相遇
问题2:操场一周是400米,小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
分 析
小华
小明
同时同地同向而行
拓展训练:
经过几秒钟两人第三次相遇?
解:设经过x秒两人第一次相遇,依题意,得
10x-5x=400,
解得x=80.
答:经过80秒两人第一次相遇
变式训练:操场一周是400米,小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行,两人同时同地相背而行,则两个人何时相遇?
分 析
小华
小明
同时同地
相背而行
解:设经过x秒两人第一次相遇,依题意,得
10x+5x=400,
解得x= .
答:经过 秒两人第一次相遇
环形跑道问题:设v甲>v乙,环形跑道长s米,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:
v甲t-v乙t=s.
①同时同地、背向而行:
v甲t+v乙t=s.
例2 小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步.小明跑2圈用的时间和他的哥哥跑3圈用的时间相等.两人同时同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
解:设小明的速度为x m/s,
则他的哥哥的速度为 x m/s,
由题意得160x=160× -400.
解得x=5.
则小明的哥哥的速度为5× =7.5(m/s).
设经过y s他们第一次相遇,
由题意,得(5+7.5)y=400.解得y=32.
答:经过32 s他们第一次相遇.
例2 顺(逆)水(风)问题一架飞机在两个城市之间飞行,当顺风飞行时需2.9 h,当逆风飞行时则需3.1 h.已知风速为20 km/h,求无风时飞机的航速和这两个城市之间的距离.
设无风时飞机的航速为x km/h,根据顺风速度=无风速度+风速,逆风速度=无风速度-风速,由路程=速度×时间列出方程,求出方程的解即可得到结果.
解:设无风时飞机的航速为x km/h,
根据题意,得2.9(x+20)=3.1(x-20).
解这个方程,得x=600.
则3.1(x-20)=1798.
因此,无风时飞机的航速为600 km/h,这两个城市之间的距离为1798 km.
1.顺(逆)风问题中的有关公式:
①顺风速度=无风速度+风速;②逆风速度=无风速度-风
速;③顺风速度-逆风速度=2×风速.
2.顺(逆)水问题中的有关公式:
①顺水速度=静水中的速度+水流速度;②逆水速度=静水
中的速度-水流速度;③顺水速度-逆水速度=2×水流速度.
例3家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
①他下山时的速度比上山时的速度每小时快1 km;
②他上山2 h到达的位置,离山顶还有1 km;
③抄近路下山,下山路程比上山路程近2 km;
④下山用1 h.
根据上面信息,他做出如下计划:
(1)在山顶游览1 h;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,
请问:孔明同学应该在什么时间从家出发?
解:设上山的速度为v km/h,
则下山的速度为(v+1) km/h,
由题意得2v+1=v+1+2,解得v=2.
即上山速度是2 km/h.
A
随堂演练
2.甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒跑6米,甲每秒跑8米.如果甲在乙前面8米处同时同向出发,那么经过几秒两人首次相遇( )
A.208秒 B.204秒
C.200秒 D.196秒
D
3.甲、乙两人赛跑,甲的速度是8米/秒,乙的速度是5米/秒,如果甲从起点处往后退20米,乙从起点处向前进10米,若甲、乙两人同时出发,则甲经过几秒钟追上乙?
解:设甲经过x秒追上乙.由题意,得8x-5x=20+10.解这个方程,得x=10.
因此,甲经过10秒追上乙.
4.A,B两地相距30千米.甲、乙两人分别从A,B两地同时出发,相向而行.已知甲比乙每小时多走1千米,经过2.5小时两人相遇,求甲、乙两人的速度.
解:设乙的速度为x千米/时,则甲的速度为(x+1)千米/时.
根据题意,得2.5x+2.5(x+1)=30.
解这个方程,得x=5.5.则x+1=6.5.
因此,甲、乙两人的速度分别为6.5千米/时、5.5千米/时.
5.甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
(2)若两车同时开出,相背而行,多少小时后两车相距1 800 km?
(3)若两车同时开出,快车在慢车后面同向而行,多少小时后两车相距1 200 km(此时快车在慢车的后面)?
解:(1)设快车开出x h后两车相遇.
由题意,得60× +90x=1 500,
解得x=9.8.
答:快车开出9.8 h后两车相遇.
(2)设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800,
解得y=2.
答:2 h后两车相距1 800 km.
(3)设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200,
解得z=10.
答:10 h后两车相距1 200 km(此时快车在慢车的
后面).
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
