河南省南阳市2020-2021学年高二下学期期末考试数学文科试题 Word版含答案
文档属性
| 名称 | 河南省南阳市2020-2021学年高二下学期期末考试数学文科试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 962.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 10:39:07 | ||
图片预览




文档简介
南阳市2021年春期高中二年级期终质量评估
数学试题(文)
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,考生做题时将答案答在答题卡的指定位置上,在本试卷上答题无效,考试时间120分钟,试卷满分150分.
2.答题前,考生务必先将自己的姓名?准考证号填写在答题卡上.
3.选择题答案使用2B铅笔填涂,非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚.
4.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.
5.保持卷面清洁,不折叠?不破损.
第I卷选择题(共60分)
一?选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知false为虚数单位,则false的值为( )
A.false B.0 C.1 D.false
2.把平面内两条直线的位置关系填入结构图中的false中,顺序较为恰当的是( )
①平行;@垂直;③相交;④斜交.
A.①②③④ B.①④②③
C.①③②④ D.②①④③
3.在二维空间中,圆的一维测度(周长)false,二维测度(面积)false;在三维空间中,球的二维测度(表面积)false,三维测度(体积)false.应用合情推理,若在四维空间中,“特级球”的三维测度false,则其四维测度false为( )
A.false B.false C.false D.false
4.已知某产品的销售额false(单位:万元)与广告费用false(单位:万元)之间的关系如下表:
false(单位:万元)
0
1
2
3
4
false(单位:万元)
10
15
false
30
35
若根据表中的数据用最小二乘法求得false与false的回归直线方程为false则下列说法中错误的是( )
A.当广告费用为10万元时,销售额一定为74万元
B.该回归直线过点false
C.产品的销售额与广告费用成正相关
D.false的值是20
5.极坐标方程false表示的图形是( )
A.两个圆
B.两条直线
C.一个圆和一条射线
D.一条直线和一条射线
6.执行下面的程序框图,若输人的false分别为false,则输出的false( )
A.false B.false C.false D.false
7.若复数false满足false,则下列说法正确的是( )
A.false的虚部为false
B.false的共轭复数为false
C.false
D.false对应的点在第二象限
8.在极坐标系中,两条曲线false的交点为false,则false( )
B.false C.2 D.1 A.4
9.若两个正实数false满足false,且不等式false有解,则实数false的取值范围是( )
A.false B.false
C.false D.false
10.点false所在轨迹的极坐标方程为false,点false所在轨迹的参数方程为false为参数false,则false的最小值是( )
A.1 B.false C.2 D.false
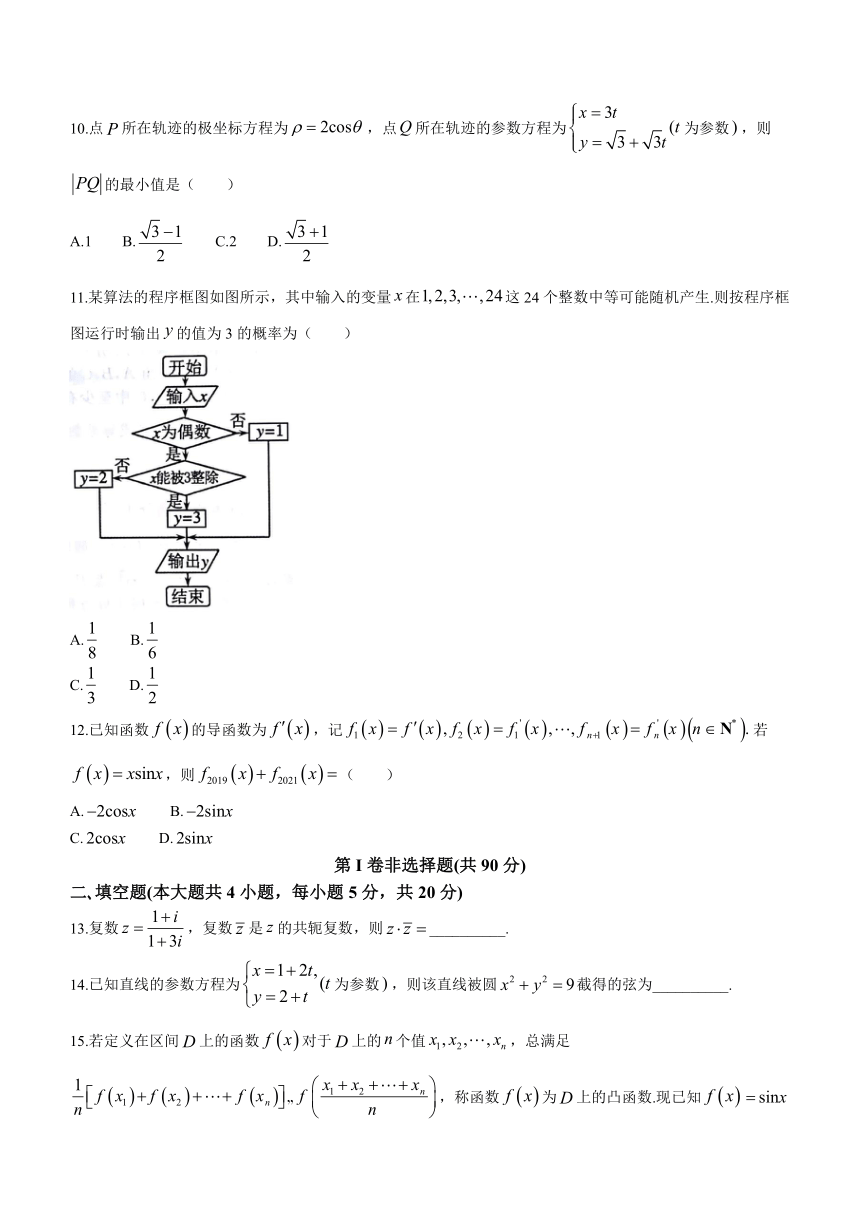
11.某算法的程序框图如图所示,其中输入的变量false在false这24个整数中等可能随机产生.则按程序框图运行时输出false的值为3的概率为( )
A.false B.false
C.false D.false
12.已知函数false的导函数为false,记false若false,则false( )
A.false B.false
C.false D.false
第I卷非选择题(共90分)
二?填空题(本大题共4小题,每小题5分,共20分)
13.复数false,复数false是false的共轭复数,则false__________.
14.已知直线的参数方程为false为参数false,则该直线被圆false截得的弦为__________.
15.若定义在区间false上的函数false对于false上的false个值false,总满足false,称函数false为false上的凸函数.现已知falsefalse在false上是凸函数,则在false中,false的最大值是__________.
16.瑞士数学家?物理学家欧拉发现任一凸多而体(即多面体任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数V?棱数E及面数F满足等式false,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮?简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,共有32个面,是由m块白色正六边形面料和false块黑色正五边形面料构成的,则m的值为__________.
三?解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
(1)在①false,②false为纯虚数,③false为非零实数,这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知复数false为虚数单位false为false的共轭复数,若__________.求实数false的值;
注:如果选择多个条件分别解答,按第一个条件给分)
(2)若false是关于false的实系数一元二次方程false的一个根,求false的值及方程的另一个根.
18.(本小题满分12分)在false中,角false的对边分别为false.
(1)求证:false中至少有一个角大于或等于false;
(2)若角false成等差数列,证明false.
19.(本小题满分12分)
在直角坐标系false中,曲线false的参数方程为false为参数false为false上的动点,false点满足false,点false的轨迹为曲线false.
(1)求false的极坐标方程;
(2)在以false为极点,false轴的正半轴为极轴的极坐标系中,射线false与false的异于极点的交点为false,与false的异于极点的交点为false,求false.
20.(本小题满分12分)
(1)已知false均为正数,且false,求证:false;
(2)根据生活常识“淡糖水再加糖会更甜”,请给出类似第(1)小题的命题,并予以证明;
(3)证明:false中,false.(可直接应用第(1);(2)小题的结论)
21.(本小题满分12分)
遵守交通规则,人人有责.“礼让行人”是我国《道路交通安全法》的明文规定,也是全国文明城市测评中的重要内容.《道路交通安全法》第17条明确规定:“机动车行经人行横道时,应当减速行驶,遇行人正在通过人行横道,应当停车让行,机动车行经没有交通信号的道路时,遇行人横过道路,应当避让,否则扣3分罚200元”,下表是2021年1至4月份我市某主干路口监控设备抓拍到的驾驶员不“礼让行人”行为统计数据:
月份
1
2
3
4
违章贺驶员人数
125
105
100
90
(1)请利用所给数据求违章人数false与月份false之间的回归直线方程false,并预测该2021年5月不“礼让行人”驾驶员的大约人数(四舍五入);
(2)交警从这4个月内通过该路口的驾驶员中随机抽查50人,调查驾驶员不“礼让行行为与驾龄的关系,得到下表:
不礼让行人
礼让行人
驾龄不超过2年
10
20
驾龄2年以上
8
12
能否据此判断有false的把握认为“礼让行人”行为与驾龄有关?参考公式false
false
false
false
false
false
false
false
false
false
false
false
false
false,其中false
22.(本小题满分12分)
在直角坐标系false中,曲线false的参数方程为false为参数false以坐标原点false为极点,false轴的正半轴为极轴建立极坐标系,曲线false的极坐标方程为false.
(1)当false时,求false和false的直角坐标方程;
(2)当false时,false与false交于false两点,设点false的直角坐标为false,求false的值.
2021年春期高中二年级期终质量评估
数学试题(文)
参考答案
一?选择题:
1-12BCBACDDCBABD
二?填空题:
13.false 14.false 15.false 16.false
三?解答题:
17.解:(1)选条件①false
false,解得false.
选条件②false为纯虚数
false,解得false
选条件③false为非零实数,false,解得false.
(2)因为false为实系数一元二次方程:false的一个根,
false,解得:false,
false原方程为false,配方得:false,解得false
false
18.解:(1)假设结论不成立,即false,
则false,这与false相矛盾,所以假设不成立,
即false中至少有一个角大于或等于false.
(2)要证false,只需证false,
即证:false,
即证false,
即:false.
又因false的三个内角false成等差数列,故false.
由余弦定理可得:false,即:false,
故false,
所以false成立
19.解:(1)因为曲线false的参数方程为false为参数),false为false上的动点,
所以可设false的坐标为false.
设false的坐标为false,由false,
得到false,消去参数得:false,
转化为极坐标方程得:false,
即曲线false的极坐标方程为:false,
同理可求false的极坐标方程:false.
(2)设false,则false,
解得:false,所以false;
设false,则false
解得:false,所以false.
所以false
20.解:(1)false均为正数,因为false,
所以false,所以false;
false
故false
(2)已知false均为正数,false,
则false,
证明:false,根据(1)知false,取倒数得到false
(3)在false中,根据正弦定理可知:false,
同理可得:false
false
false
21.解:(1)由表中数据易求:
false,
则false
false,
故所求回归直线方程为false,
令false,则false人,
预测该路口5月份不“礼让行人”的司坡员大约人数为78人.
(2)由表中数据可得:false,
对比表中数据可知,没有false的把握认为“礼让行人”行为与驾龄有关.
22.解:(1)曲线false的参数方程为false为参数false,
消去false得:false;
当false时,曲线false的极坐标方程为false,
即false,转化为直角坐标方程为false;
即false的直角坐标方程为:false的直角坐标方程为:false;
(2)当false时,false的直角坐标方程为:false,
将false的参数方程为false代入,整理得:false,
设false对应的参数分别为false,则false,
易知:false与false异号,
所以false.
数学试题(文)
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,考生做题时将答案答在答题卡的指定位置上,在本试卷上答题无效,考试时间120分钟,试卷满分150分.
2.答题前,考生务必先将自己的姓名?准考证号填写在答题卡上.
3.选择题答案使用2B铅笔填涂,非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚.
4.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.
5.保持卷面清洁,不折叠?不破损.
第I卷选择题(共60分)
一?选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知false为虚数单位,则false的值为( )
A.false B.0 C.1 D.false
2.把平面内两条直线的位置关系填入结构图中的false中,顺序较为恰当的是( )
①平行;@垂直;③相交;④斜交.
A.①②③④ B.①④②③
C.①③②④ D.②①④③
3.在二维空间中,圆的一维测度(周长)false,二维测度(面积)false;在三维空间中,球的二维测度(表面积)false,三维测度(体积)false.应用合情推理,若在四维空间中,“特级球”的三维测度false,则其四维测度false为( )
A.false B.false C.false D.false
4.已知某产品的销售额false(单位:万元)与广告费用false(单位:万元)之间的关系如下表:
false(单位:万元)
0
1
2
3
4
false(单位:万元)
10
15
false
30
35
若根据表中的数据用最小二乘法求得false与false的回归直线方程为false则下列说法中错误的是( )
A.当广告费用为10万元时,销售额一定为74万元
B.该回归直线过点false
C.产品的销售额与广告费用成正相关
D.false的值是20
5.极坐标方程false表示的图形是( )
A.两个圆
B.两条直线
C.一个圆和一条射线
D.一条直线和一条射线
6.执行下面的程序框图,若输人的false分别为false,则输出的false( )
A.false B.false C.false D.false
7.若复数false满足false,则下列说法正确的是( )
A.false的虚部为false
B.false的共轭复数为false
C.false
D.false对应的点在第二象限
8.在极坐标系中,两条曲线false的交点为false,则false( )
B.false C.2 D.1 A.4
9.若两个正实数false满足false,且不等式false有解,则实数false的取值范围是( )
A.false B.false
C.false D.false
10.点false所在轨迹的极坐标方程为false,点false所在轨迹的参数方程为false为参数false,则false的最小值是( )
A.1 B.false C.2 D.false
11.某算法的程序框图如图所示,其中输入的变量false在false这24个整数中等可能随机产生.则按程序框图运行时输出false的值为3的概率为( )
A.false B.false
C.false D.false
12.已知函数false的导函数为false,记false若false,则false( )
A.false B.false
C.false D.false
第I卷非选择题(共90分)
二?填空题(本大题共4小题,每小题5分,共20分)
13.复数false,复数false是false的共轭复数,则false__________.
14.已知直线的参数方程为false为参数false,则该直线被圆false截得的弦为__________.
15.若定义在区间false上的函数false对于false上的false个值false,总满足false,称函数false为false上的凸函数.现已知falsefalse在false上是凸函数,则在false中,false的最大值是__________.
16.瑞士数学家?物理学家欧拉发现任一凸多而体(即多面体任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数V?棱数E及面数F满足等式false,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮?简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,共有32个面,是由m块白色正六边形面料和false块黑色正五边形面料构成的,则m的值为__________.
三?解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
(1)在①false,②false为纯虚数,③false为非零实数,这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知复数false为虚数单位false为false的共轭复数,若__________.求实数false的值;
注:如果选择多个条件分别解答,按第一个条件给分)
(2)若false是关于false的实系数一元二次方程false的一个根,求false的值及方程的另一个根.
18.(本小题满分12分)在false中,角false的对边分别为false.
(1)求证:false中至少有一个角大于或等于false;
(2)若角false成等差数列,证明false.
19.(本小题满分12分)
在直角坐标系false中,曲线false的参数方程为false为参数false为false上的动点,false点满足false,点false的轨迹为曲线false.
(1)求false的极坐标方程;
(2)在以false为极点,false轴的正半轴为极轴的极坐标系中,射线false与false的异于极点的交点为false,与false的异于极点的交点为false,求false.
20.(本小题满分12分)
(1)已知false均为正数,且false,求证:false;
(2)根据生活常识“淡糖水再加糖会更甜”,请给出类似第(1)小题的命题,并予以证明;
(3)证明:false中,false.(可直接应用第(1);(2)小题的结论)
21.(本小题满分12分)
遵守交通规则,人人有责.“礼让行人”是我国《道路交通安全法》的明文规定,也是全国文明城市测评中的重要内容.《道路交通安全法》第17条明确规定:“机动车行经人行横道时,应当减速行驶,遇行人正在通过人行横道,应当停车让行,机动车行经没有交通信号的道路时,遇行人横过道路,应当避让,否则扣3分罚200元”,下表是2021年1至4月份我市某主干路口监控设备抓拍到的驾驶员不“礼让行人”行为统计数据:
月份
1
2
3
4
违章贺驶员人数
125
105
100
90
(1)请利用所给数据求违章人数false与月份false之间的回归直线方程false,并预测该2021年5月不“礼让行人”驾驶员的大约人数(四舍五入);
(2)交警从这4个月内通过该路口的驾驶员中随机抽查50人,调查驾驶员不“礼让行行为与驾龄的关系,得到下表:
不礼让行人
礼让行人
驾龄不超过2年
10
20
驾龄2年以上
8
12
能否据此判断有false的把握认为“礼让行人”行为与驾龄有关?参考公式false
false
false
false
false
false
false
false
false
false
false
false
false
false,其中false
22.(本小题满分12分)
在直角坐标系false中,曲线false的参数方程为false为参数false以坐标原点false为极点,false轴的正半轴为极轴建立极坐标系,曲线false的极坐标方程为false.
(1)当false时,求false和false的直角坐标方程;
(2)当false时,false与false交于false两点,设点false的直角坐标为false,求false的值.
2021年春期高中二年级期终质量评估
数学试题(文)
参考答案
一?选择题:
1-12BCBACDDCBABD
二?填空题:
13.false 14.false 15.false 16.false
三?解答题:
17.解:(1)选条件①false
false,解得false.
选条件②false为纯虚数
false,解得false
选条件③false为非零实数,false,解得false.
(2)因为false为实系数一元二次方程:false的一个根,
false,解得:false,
false原方程为false,配方得:false,解得false
false
18.解:(1)假设结论不成立,即false,
则false,这与false相矛盾,所以假设不成立,
即false中至少有一个角大于或等于false.
(2)要证false,只需证false,
即证:false,
即证false,
即:false.
又因false的三个内角false成等差数列,故false.
由余弦定理可得:false,即:false,
故false,
所以false成立
19.解:(1)因为曲线false的参数方程为false为参数),false为false上的动点,
所以可设false的坐标为false.
设false的坐标为false,由false,
得到false,消去参数得:false,
转化为极坐标方程得:false,
即曲线false的极坐标方程为:false,
同理可求false的极坐标方程:false.
(2)设false,则false,
解得:false,所以false;
设false,则false
解得:false,所以false.
所以false
20.解:(1)false均为正数,因为false,
所以false,所以false;
false
故false
(2)已知false均为正数,false,
则false,
证明:false,根据(1)知false,取倒数得到false
(3)在false中,根据正弦定理可知:false,
同理可得:false
false
false
21.解:(1)由表中数据易求:
false,
则false
false,
故所求回归直线方程为false,
令false,则false人,
预测该路口5月份不“礼让行人”的司坡员大约人数为78人.
(2)由表中数据可得:false,
对比表中数据可知,没有false的把握认为“礼让行人”行为与驾龄有关.
22.解:(1)曲线false的参数方程为false为参数false,
消去false得:false;
当false时,曲线false的极坐标方程为false,
即false,转化为直角坐标方程为false;
即false的直角坐标方程为:false的直角坐标方程为:false;
(2)当false时,false的直角坐标方程为:false,
将false的参数方程为false代入,整理得:false,
设false对应的参数分别为false,则false,
易知:false与false异号,
所以false.
同课章节目录
