四年级下册数学课件-梯形的面积| 青岛版(五四学制)(20张ppt)
文档属性
| 名称 | 四年级下册数学课件-梯形的面积| 青岛版(五四学制)(20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 17:12:07 | ||
图片预览





文档简介
(共20张PPT)
梯形的面积
梯形的面积
底
长
高
宽
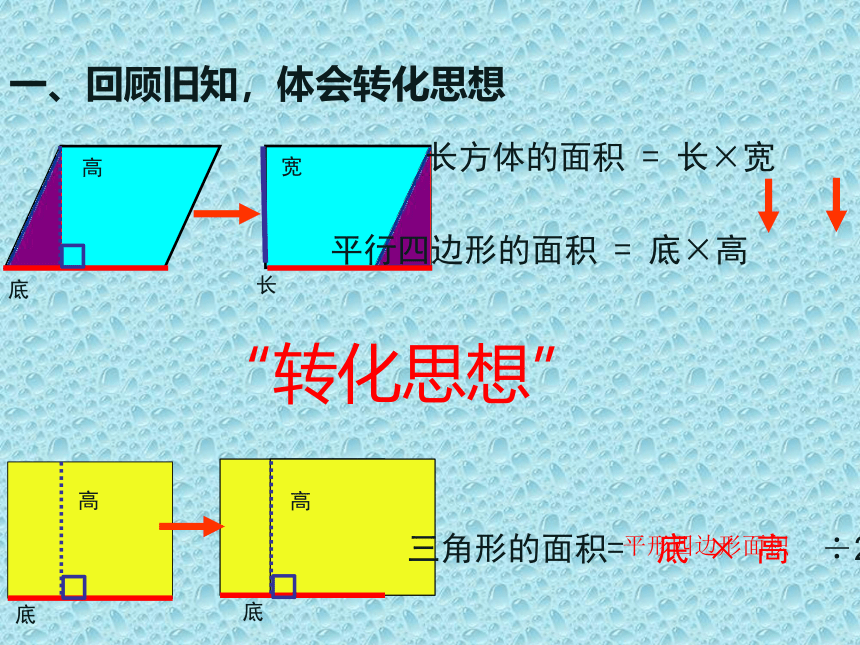
长方体的面积
=
长×宽
平行四边形的面积
=
底×高
底
底
高
高
三角形的面积=
÷2
平形四边形面积
底
×
高
一、回顾旧知,体会转化思想
“转化思想”
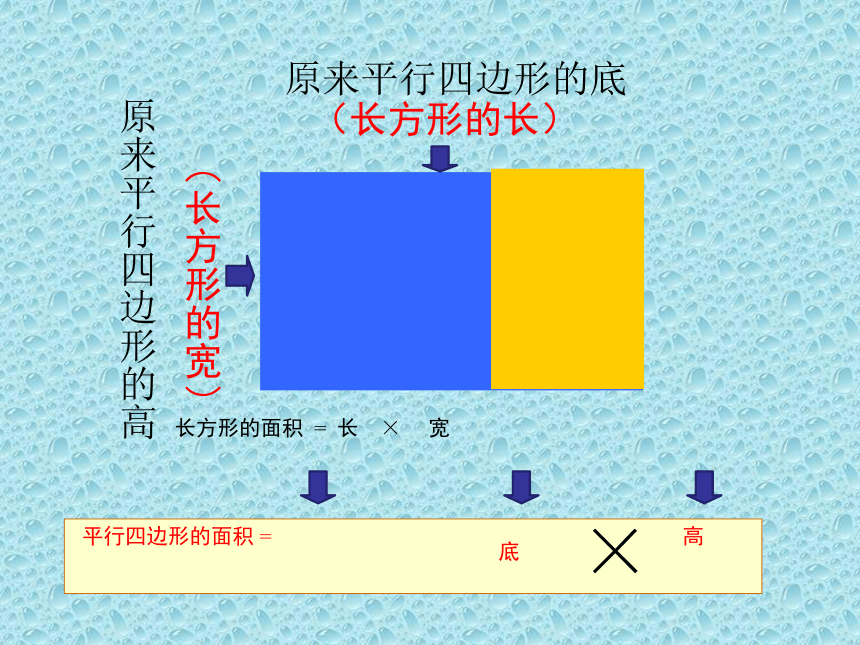
平行四边形的面积
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
长方形的面积
=
长
×
宽
平行四边形的面积
=
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
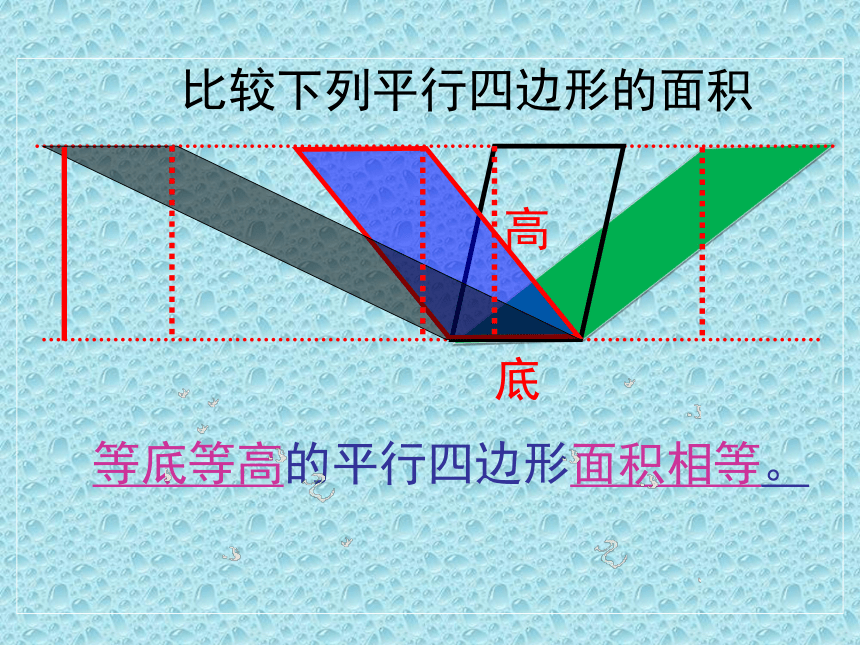
比较下列平行四边形的面积
高
底
等底等高的平行四边形面积相等。
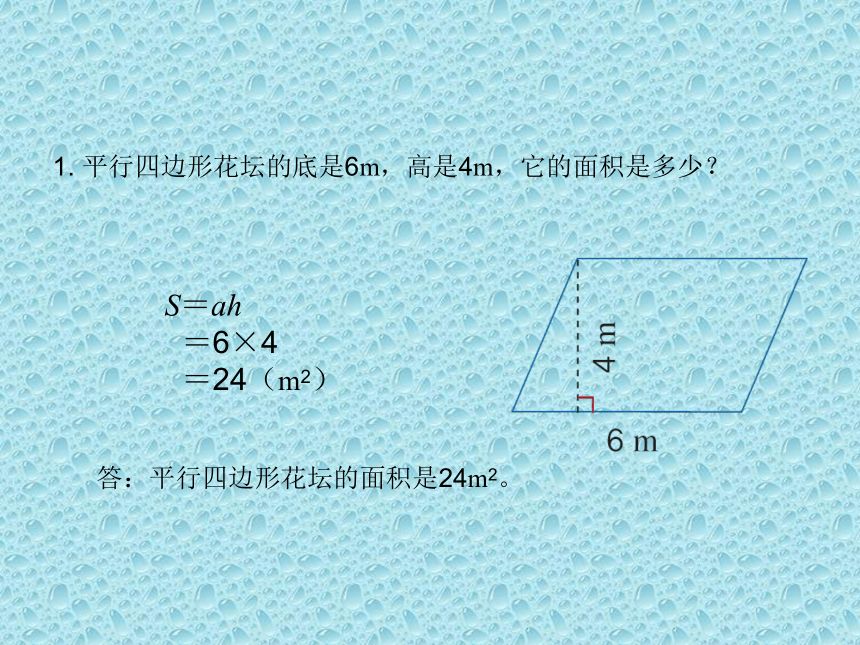
1.
平行四边形花坛的底是6m,高是4m,它的面积是多少?
S=ah
=6×4
=24(m2)
答:平行四边形花坛的面积是24m2。
试一试
:
能不能把梯形也转化成已学过的图形来求面积呢?
边操作边思考:
(1)拼成的图形的底与梯形的上底、下底有什么关系?
(2)拼成的图形的高与梯形的高有什么关系?
(3)拼成的图形的面积与梯形的面积有什么关系?
二、尝试操作,探究新知
梯形的面积=
平形四边形的面积÷2
下底
上底
=
底
×
高
÷2
=(上底+下底)
高
×高
÷2
二、尝试操作,探究新知
上底
下底
高
高
①
②
梯形的面积=①号三角形的面积+②号三角形的面积
①号三角形的面积=
×高÷2
底
上底
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
②号三角形的面积=
×高÷2
底
下底
高÷2
上底
+
下底
梯形的面积=
平形四边形的面积
=
底
×
高
=(上底+下底)
×高÷2
二、尝试操作,探究新知
我是小法官
(
1
)两个面积相等的梯形一定能拼成一个
平行四边形。
(
)
(
3
)任何一个梯形都可以分成两个等高的
三角形。
(
)
×
(
2
)梯形的面积是平行四边形面积的一半。
(
)
√
(
4
)一个长方体木梯形的上底下底越长,面
积越大。
(
)
×
×
我国三峡水电站大坝的横截面的一部分是梯形(如图),求它的的面积。
36m
120m
135m
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
4
cm
8
cm
3
cm
6
dm
6
dm
10
dm
(
8
+4
)×
3
÷
2
(
6
+10
)×
6
÷
2
=12×
3
÷
2
=36
÷
2
=18
(平方厘米)
=16×
6
÷
2
=96
÷
2
=48(平方分米)
四、总结方法,提炼思想
新问题
旧知识
转化
仔细观察,寻找关系
谢谢大家!
谢谢大家!
梯形的面积
梯形的面积
底
长
高
宽
长方体的面积
=
长×宽
平行四边形的面积
=
底×高
底
底
高
高
三角形的面积=
÷2
平形四边形面积
底
×
高
一、回顾旧知,体会转化思想
“转化思想”
平行四边形的面积
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
长方形的面积
=
长
×
宽
平行四边形的面积
=
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
比较下列平行四边形的面积
高
底
等底等高的平行四边形面积相等。
1.
平行四边形花坛的底是6m,高是4m,它的面积是多少?
S=ah
=6×4
=24(m2)
答:平行四边形花坛的面积是24m2。
试一试
:
能不能把梯形也转化成已学过的图形来求面积呢?
边操作边思考:
(1)拼成的图形的底与梯形的上底、下底有什么关系?
(2)拼成的图形的高与梯形的高有什么关系?
(3)拼成的图形的面积与梯形的面积有什么关系?
二、尝试操作,探究新知
梯形的面积=
平形四边形的面积÷2
下底
上底
=
底
×
高
÷2
=(上底+下底)
高
×高
÷2
二、尝试操作,探究新知
上底
下底
高
高
①
②
梯形的面积=①号三角形的面积+②号三角形的面积
①号三角形的面积=
×高÷2
底
上底
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
②号三角形的面积=
×高÷2
底
下底
高÷2
上底
+
下底
梯形的面积=
平形四边形的面积
=
底
×
高
=(上底+下底)
×高÷2
二、尝试操作,探究新知
我是小法官
(
1
)两个面积相等的梯形一定能拼成一个
平行四边形。
(
)
(
3
)任何一个梯形都可以分成两个等高的
三角形。
(
)
×
(
2
)梯形的面积是平行四边形面积的一半。
(
)
√
(
4
)一个长方体木梯形的上底下底越长,面
积越大。
(
)
×
×
我国三峡水电站大坝的横截面的一部分是梯形(如图),求它的的面积。
36m
120m
135m
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
4
cm
8
cm
3
cm
6
dm
6
dm
10
dm
(
8
+4
)×
3
÷
2
(
6
+10
)×
6
÷
2
=12×
3
÷
2
=36
÷
2
=18
(平方厘米)
=16×
6
÷
2
=96
÷
2
=48(平方分米)
四、总结方法,提炼思想
新问题
旧知识
转化
仔细观察,寻找关系
谢谢大家!
谢谢大家!
