四年级下册数学课件-2.3 梯形的面积| 青岛版(五四学制)(17张ppt )
文档属性
| 名称 | 四年级下册数学课件-2.3 梯形的面积| 青岛版(五四学制)(17张ppt ) |

|
|
| 格式 | ppt | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
梯形的面积
回顾反思
自主练习
合作探索
情境导入
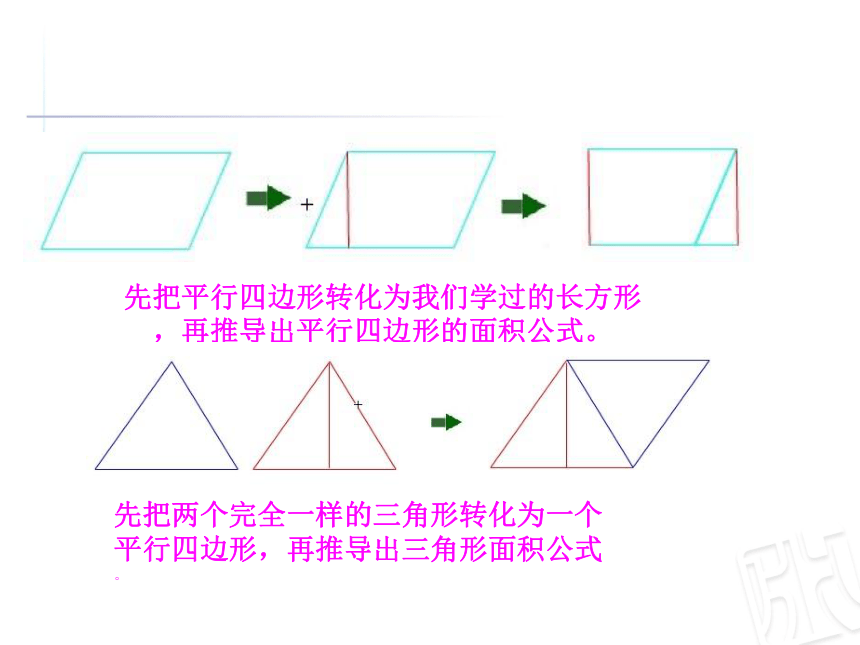
先把平行四边形转化为我们学过的长方形,再推导出平行四边形的面积公式。
先把两个完全一样的三角形转化为一个平行四边形,再推导出三角形面积公式。
一、情境导入
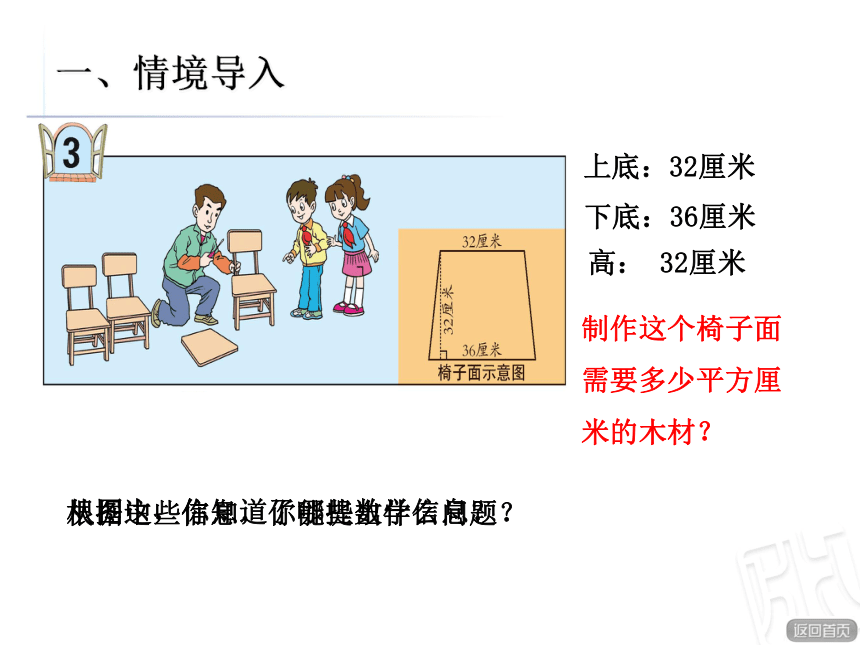
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
上底:32厘米
下底:36厘米
高:
32厘米
制作这个椅子面需要多少平方厘米的木材?
制作这个椅子面需要多少平方厘米的木材?
1.想一想。求椅子面的面积,实际上就是求什么图形的面积?
2.猜一猜。可以把梯形转化成什么图形来研究?会验证你的猜想吗?
3.做一做。利用学具(两个完全相同的梯形)拼一拼,摆一摆,看看你有什么发现。
探索活动要求
二、合作探索
上底
下底
黄三角形面积=下底×高÷2
红三角形面积=上底×高÷2
梯形面积=黄三角形面积+红三角形面积
=下底×高÷2
+上底×高÷2
高
×高÷2
×高÷2
上底
下底
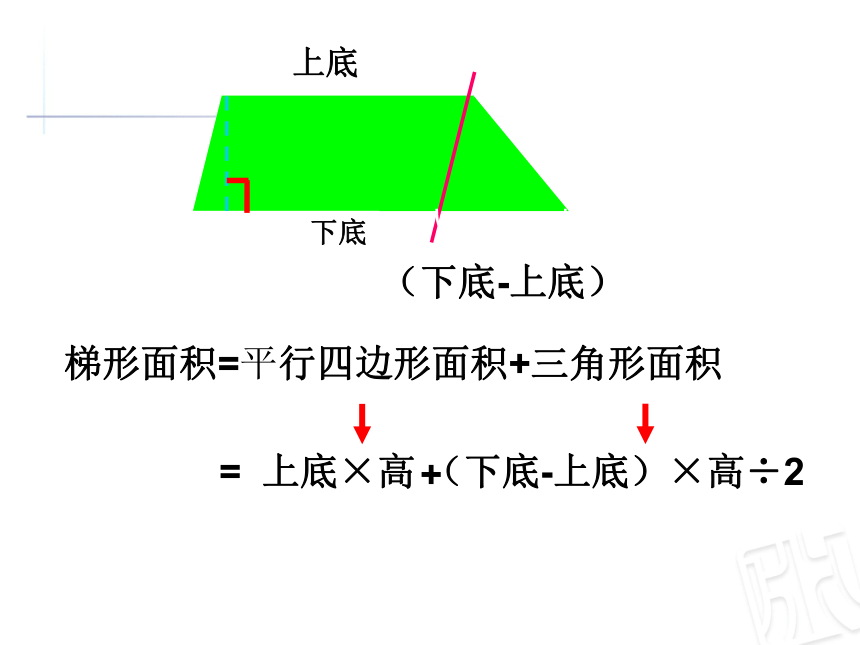
梯形面积=平行四边形面积+三角形面积
上底×高
(下底-上底)×高÷2
(下底-上底)
=
+
长方形的面积
=
长
×
宽
高
×
(
)
上底+下底
2个梯形面积
=
上底
下底
高
平行四边形的面积
=
底
×
高
上底+下底
高
×
(
)
上底
下底
2个梯形面积
=
平行四边形的面积
=
底
×
高
上底+下底
高
×
(
)
上底
下底
2个梯形面积
=
÷2
梯形面积=(上底+下底)×高
(32+36)×32÷2
二、合作探索
制作这个椅子面需要多少平方厘米的木材?
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
你知道吗?
大约在2000年前,我国数学名著《九章算术》中的方田章就论述了梯形面积的算法。书中说:“并两邪而半之,以乘正纵若广。又可半正纵若广,以并,亩法而一。”就是说:梯形面积=(上底+下底)
×
高÷2。并且还详细记录了不同推导方法的过程。《九章算术》是中国古代数学专著,是当时世界上最先进的应用数学。
试一试
1.想一想,填一填。
(1)
梯形的面积=(
),用字母表示是(
)。
(2)
一个梯形的上底是5
cm,下底是9
cm,高是6
cm,两个这样的梯形拼成的平行四边形的一个底是( )
cm,该底上的高是( )cm。
(3)
一个梯形的上底增加3
cm,下底减少3
cm,高不变,面积( )(填“变大”“变小”或“不变”)。
三、课堂练习
(选题源于《典中点》)
(上底+下底)×高÷2
S=(a+b)h÷2
6
14
不变
2.求下面梯形的面积。(单位:
cm)
(1)
(2)
三、课堂练习
(5+11)×4÷2=32(cm2)
(7+11)×5÷2=45(cm2)
3.解决下列问题。
(1)
一条水渠的横截面是一个梯形,渠口宽2.2
m,渠底宽1.4
m,渠深1.5
m。它的横截面的面积是多少平方米?
三、课堂练习
(2.2+1.4)×1.5÷2=2.7(m2)
答:它的横截面的面积是2.7
m2。
(2)
一块橘子园的地面形状是梯形,它的上底是120米,下底是160米,高是50米。如果每棵橘子树占地10平方米,这块地种了多少棵橘子树?
三、课堂练习
(120+160)×50÷2÷10=700(棵)
答:这块地种了700棵橘子树。
(3)
一块梯形土地的面积是45平方米,下底是10米,上底是5米,它的高是多少米?
三、课堂练习
45×2÷(10+5)=6(米)
答:它的高是6米。
四、回顾反思
梯形的面积
回顾反思
自主练习
合作探索
情境导入
先把平行四边形转化为我们学过的长方形,再推导出平行四边形的面积公式。
先把两个完全一样的三角形转化为一个平行四边形,再推导出三角形面积公式。
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
上底:32厘米
下底:36厘米
高:
32厘米
制作这个椅子面需要多少平方厘米的木材?
制作这个椅子面需要多少平方厘米的木材?
1.想一想。求椅子面的面积,实际上就是求什么图形的面积?
2.猜一猜。可以把梯形转化成什么图形来研究?会验证你的猜想吗?
3.做一做。利用学具(两个完全相同的梯形)拼一拼,摆一摆,看看你有什么发现。
探索活动要求
二、合作探索
上底
下底
黄三角形面积=下底×高÷2
红三角形面积=上底×高÷2
梯形面积=黄三角形面积+红三角形面积
=下底×高÷2
+上底×高÷2
高
×高÷2
×高÷2
上底
下底
梯形面积=平行四边形面积+三角形面积
上底×高
(下底-上底)×高÷2
(下底-上底)
=
+
长方形的面积
=
长
×
宽
高
×
(
)
上底+下底
2个梯形面积
=
上底
下底
高
平行四边形的面积
=
底
×
高
上底+下底
高
×
(
)
上底
下底
2个梯形面积
=
平行四边形的面积
=
底
×
高
上底+下底
高
×
(
)
上底
下底
2个梯形面积
=
÷2
梯形面积=(上底+下底)×高
(32+36)×32÷2
二、合作探索
制作这个椅子面需要多少平方厘米的木材?
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
你知道吗?
大约在2000年前,我国数学名著《九章算术》中的方田章就论述了梯形面积的算法。书中说:“并两邪而半之,以乘正纵若广。又可半正纵若广,以并,亩法而一。”就是说:梯形面积=(上底+下底)
×
高÷2。并且还详细记录了不同推导方法的过程。《九章算术》是中国古代数学专著,是当时世界上最先进的应用数学。
试一试
1.想一想,填一填。
(1)
梯形的面积=(
),用字母表示是(
)。
(2)
一个梯形的上底是5
cm,下底是9
cm,高是6
cm,两个这样的梯形拼成的平行四边形的一个底是( )
cm,该底上的高是( )cm。
(3)
一个梯形的上底增加3
cm,下底减少3
cm,高不变,面积( )(填“变大”“变小”或“不变”)。
三、课堂练习
(选题源于《典中点》)
(上底+下底)×高÷2
S=(a+b)h÷2
6
14
不变
2.求下面梯形的面积。(单位:
cm)
(1)
(2)
三、课堂练习
(5+11)×4÷2=32(cm2)
(7+11)×5÷2=45(cm2)
3.解决下列问题。
(1)
一条水渠的横截面是一个梯形,渠口宽2.2
m,渠底宽1.4
m,渠深1.5
m。它的横截面的面积是多少平方米?
三、课堂练习
(2.2+1.4)×1.5÷2=2.7(m2)
答:它的横截面的面积是2.7
m2。
(2)
一块橘子园的地面形状是梯形,它的上底是120米,下底是160米,高是50米。如果每棵橘子树占地10平方米,这块地种了多少棵橘子树?
三、课堂练习
(120+160)×50÷2÷10=700(棵)
答:这块地种了700棵橘子树。
(3)
一块梯形土地的面积是45平方米,下底是10米,上底是5米,它的高是多少米?
三、课堂练习
45×2÷(10+5)=6(米)
答:它的高是6米。
四、回顾反思
