七年级数学二元一次方程组
图片预览







文档简介
(共25张PPT)
魏庄中学 刘杰
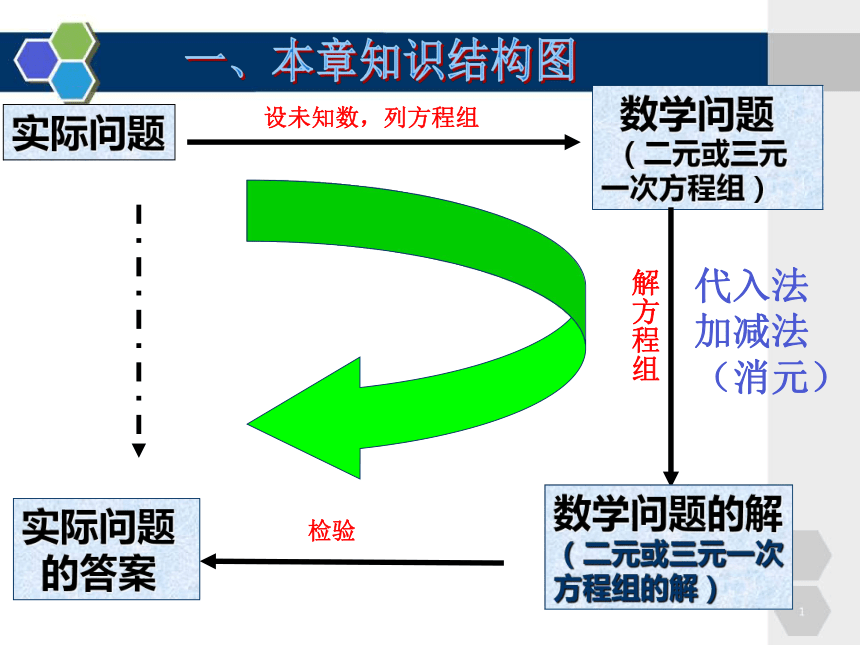
实际问题
设未知数,列方程组
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题
的答案
代入法
加减法
(消元)
二、有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:
使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.
三、方程组的解法
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
1.变形(求表达式):从方程组中选一个系数比较简单的方程,将此方程中的一个未知数,如y,用含x的代数式表示;
2.代入:把这个含x的代数式代入另一个方程中,消去y,得到一个关于x的一元一次方程;
3.求解:解一元一次方程,求出x的值;
4.回代:再把求出的x的值 代入变形后的方程,求出y的值.
5.结果:写出原方程组的解.
用加减法解二元一次方程组的步骤:
1.变形(变系数):利用等式性质把一个或两个方
程的两边都乘以适当的数,变换两个方程的同一
个未知数的系数,使其绝对值相等;
2.加(减):把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
3.求解:解这个一元一次方程,求得一个未知数
的值 ;
4.代入:把所求的这个未知的值代入方程组中较
为简便的一个方程,求出另一个未知数,从而得
到方程的解 .
5.结果:写出原方程组的解.
四、知识应用
1.下列方程是二元一次方程的是____
A.xy+8=0 B.
C. D.
2已知方程
3.已知x=2,y=1是方程kx-y=3的解,则k=( )
4.已知方程2x-5y=11,用含x的式子表示y为__________用含x的式子表y__________
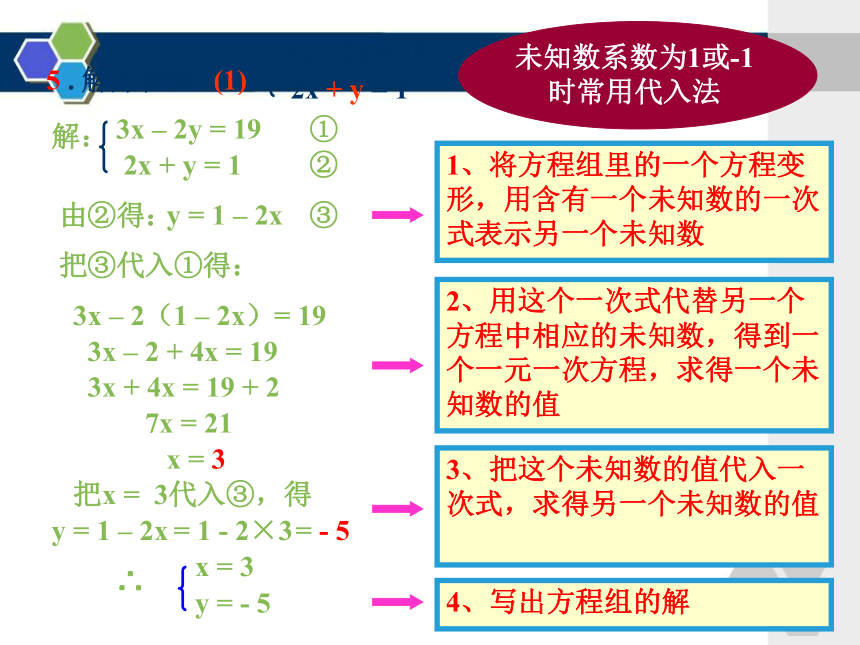
5 . 解方程组: (1)
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
未知数系数为1或-1时常用代入法
解:
①×2,得:
4x+6y=38 ③
②×3,得:
9x-6y=27 ④
③+④,得:
13x=65 x=5
把x=5代入①,得:
y=3
∴
思考:在例2中,你还能用什么方法解题?
(2).
加减法消元时,先要把相同未知数的系数化为相同或相反
(3).
复杂方程先化简
②
①
1.若点P(x-y,3x+y)与点Q(-1,-5)关于X轴对称,则x+y=______.
3
2.已知|2x+3y+5|+(3x+2Y-25)2=0,
则x-y=______.
-30
3.若两个多边形的边数之比是2:3,两个多边形的内角和是1980°,求这两个多边形的边数.
6和9
5.方程组 中,x与y的和为
12,求k的值.
K=14
4.方程组 中,x与y的和为
12,求k的值.
四.应用题:
列方程组解应用题的一般步骤:
1.审 2.设 3.列 4.解 5.答
一.行程问题:
1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程=原来相距路
程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速
例1.A、B两地相距36千米.甲从A地出发步行到B地,乙从B地出发步行到A地.两人同时出发,4小时相遇,6小时后 ,甲所余路程为乙所余路程的2倍,求两人的速度.
解:设甲、乙的速度分别为x千米/小时和y千米/小时.
依题意可得:
解得
答:甲、乙的速度分别为4千米/小时和5千米/小时.
例2.某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离.
、
例3.甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次.已知甲比乙跑得快,甲、乙每分钟各跑多少圈
1.某学校现有甲种材料35㎏,乙种材料29㎏,制作A.B两种型号的工艺品,用料情况如下表:
需甲种材料 需乙种材料
1件A型工艺品 0.9㎏ 0.3㎏
1件B型工艺品 0.4㎏
1㎏
(1)利用这些材料能制作A.B两种工艺品各多少件
(2)若每公斤甲.乙种材料分别为8元和10元,问制作A.B两种型号的工艺品各需材料多少钱
二.图表问题
2.某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
每亩所需劳动力(个) 每亩预计产值(元)
蔬菜 3000
水稻 700
(1)为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力多少人?
(2)这时预计产值是多少?
3.入世后,国内各汽车企业展开价格大战,汽车价格大幅下降,有些型号的汽车供不应求。某汽车生产厂接受了一份订单,要在规定的日期内生产一批汽车,如果每天生产35辆,则差10辆完成任务,如果每天生产40辆,则可提前半天完成任务,问订单要多少辆汽车,规定日期是多少天?
三.总量不变问题
4.某中学组织初一学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出了一辆车,且其余客车恰好坐满.已知45座客车日租金为每辆220元, 60座客车日租金为每辆300元,试问:(1)初一年级的人数是多少 原计划租用45座客车多少辆 (2)若租用同一种车,要使每位同学都有座位,怎样租用更合算
(四).销售问题:
标价×折扣=售价
售价-进价=利润
利润率=
练习:
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元.问:比不打折少花多少钱
魏庄中学 刘杰
实际问题
设未知数,列方程组
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题
的答案
代入法
加减法
(消元)
二、有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:
使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.
三、方程组的解法
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
1.变形(求表达式):从方程组中选一个系数比较简单的方程,将此方程中的一个未知数,如y,用含x的代数式表示;
2.代入:把这个含x的代数式代入另一个方程中,消去y,得到一个关于x的一元一次方程;
3.求解:解一元一次方程,求出x的值;
4.回代:再把求出的x的值 代入变形后的方程,求出y的值.
5.结果:写出原方程组的解.
用加减法解二元一次方程组的步骤:
1.变形(变系数):利用等式性质把一个或两个方
程的两边都乘以适当的数,变换两个方程的同一
个未知数的系数,使其绝对值相等;
2.加(减):把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
3.求解:解这个一元一次方程,求得一个未知数
的值 ;
4.代入:把所求的这个未知的值代入方程组中较
为简便的一个方程,求出另一个未知数,从而得
到方程的解 .
5.结果:写出原方程组的解.
四、知识应用
1.下列方程是二元一次方程的是____
A.xy+8=0 B.
C. D.
2已知方程
3.已知x=2,y=1是方程kx-y=3的解,则k=( )
4.已知方程2x-5y=11,用含x的式子表示y为__________用含x的式子表y__________
5 . 解方程组: (1)
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
未知数系数为1或-1时常用代入法
解:
①×2,得:
4x+6y=38 ③
②×3,得:
9x-6y=27 ④
③+④,得:
13x=65 x=5
把x=5代入①,得:
y=3
∴
思考:在例2中,你还能用什么方法解题?
(2).
加减法消元时,先要把相同未知数的系数化为相同或相反
(3).
复杂方程先化简
②
①
1.若点P(x-y,3x+y)与点Q(-1,-5)关于X轴对称,则x+y=______.
3
2.已知|2x+3y+5|+(3x+2Y-25)2=0,
则x-y=______.
-30
3.若两个多边形的边数之比是2:3,两个多边形的内角和是1980°,求这两个多边形的边数.
6和9
5.方程组 中,x与y的和为
12,求k的值.
K=14
4.方程组 中,x与y的和为
12,求k的值.
四.应用题:
列方程组解应用题的一般步骤:
1.审 2.设 3.列 4.解 5.答
一.行程问题:
1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程=原来相距路
程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速
例1.A、B两地相距36千米.甲从A地出发步行到B地,乙从B地出发步行到A地.两人同时出发,4小时相遇,6小时后 ,甲所余路程为乙所余路程的2倍,求两人的速度.
解:设甲、乙的速度分别为x千米/小时和y千米/小时.
依题意可得:
解得
答:甲、乙的速度分别为4千米/小时和5千米/小时.
例2.某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离.
、
例3.甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次.已知甲比乙跑得快,甲、乙每分钟各跑多少圈
1.某学校现有甲种材料35㎏,乙种材料29㎏,制作A.B两种型号的工艺品,用料情况如下表:
需甲种材料 需乙种材料
1件A型工艺品 0.9㎏ 0.3㎏
1件B型工艺品 0.4㎏
1㎏
(1)利用这些材料能制作A.B两种工艺品各多少件
(2)若每公斤甲.乙种材料分别为8元和10元,问制作A.B两种型号的工艺品各需材料多少钱
二.图表问题
2.某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
每亩所需劳动力(个) 每亩预计产值(元)
蔬菜 3000
水稻 700
(1)为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力多少人?
(2)这时预计产值是多少?
3.入世后,国内各汽车企业展开价格大战,汽车价格大幅下降,有些型号的汽车供不应求。某汽车生产厂接受了一份订单,要在规定的日期内生产一批汽车,如果每天生产35辆,则差10辆完成任务,如果每天生产40辆,则可提前半天完成任务,问订单要多少辆汽车,规定日期是多少天?
三.总量不变问题
4.某中学组织初一学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出了一辆车,且其余客车恰好坐满.已知45座客车日租金为每辆220元, 60座客车日租金为每辆300元,试问:(1)初一年级的人数是多少 原计划租用45座客车多少辆 (2)若租用同一种车,要使每位同学都有座位,怎样租用更合算
(四).销售问题:
标价×折扣=售价
售价-进价=利润
利润率=
练习:
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元.问:比不打折少花多少钱
