七年级数学实际问题与二元一次方程组
文档属性
| 名称 | 七年级数学实际问题与二元一次方程组 |

|
|
| 格式 | zip | ||
| 文件大小 | 380.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-14 00:00:00 | ||
图片预览






文档简介
(共30张PPT)
8.3 实际问题与二元一次方程组(3)
走近生活 探究知识 享受快乐
1、公路的运价为1.5元/(吨·千米),
里程为10km,货物重量为200吨,
则公路运费= .
1.5×10×200
2、铁路的运价为1.2元/(吨·千米),
原料重量为100吨,里程为20km,
则铁路运费= .
1.2×20×100
探究:
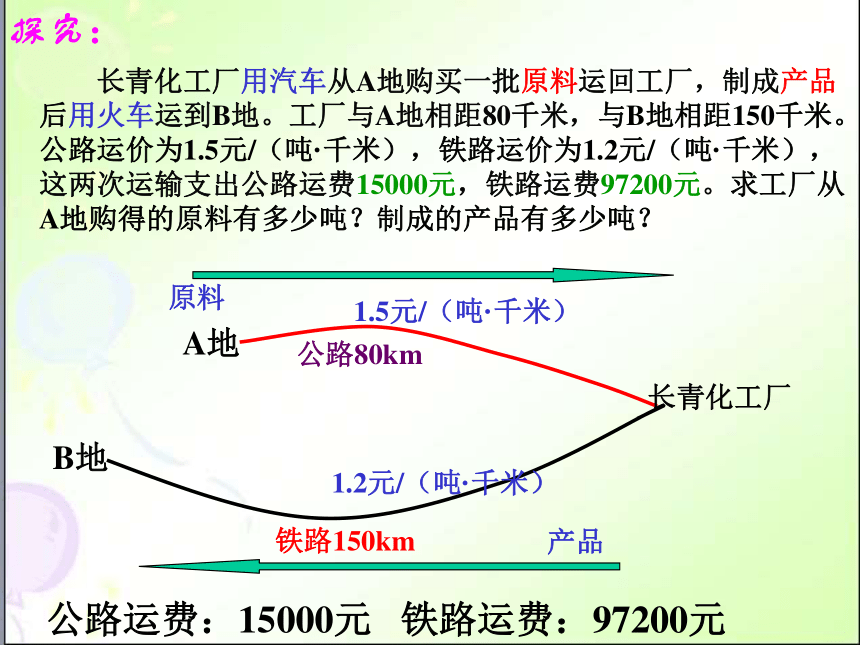
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费
15000元,铁路运费97200元。求工厂从A地购得的原料
有多少吨?制成的产品有多少吨?
分析:题中的量很多,并且相互关联,这时,我们可画一张示意图,把题中的条件在图中标出来,这样比较直,能帮助我们比较顺利地找出题中的相等关系。
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
探究:
探究:
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),
这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
解:制成的产品为x 吨,设购得的原料为y吨,
根据题意得
{
1.5 × 80 ×y =15000
1.2×150 ×x =97200
解得:
{
x=540
y=125
答:购得的原料为125吨, 制成的产品为540 吨。
画示意图是解决道路运输问题的手段之一。
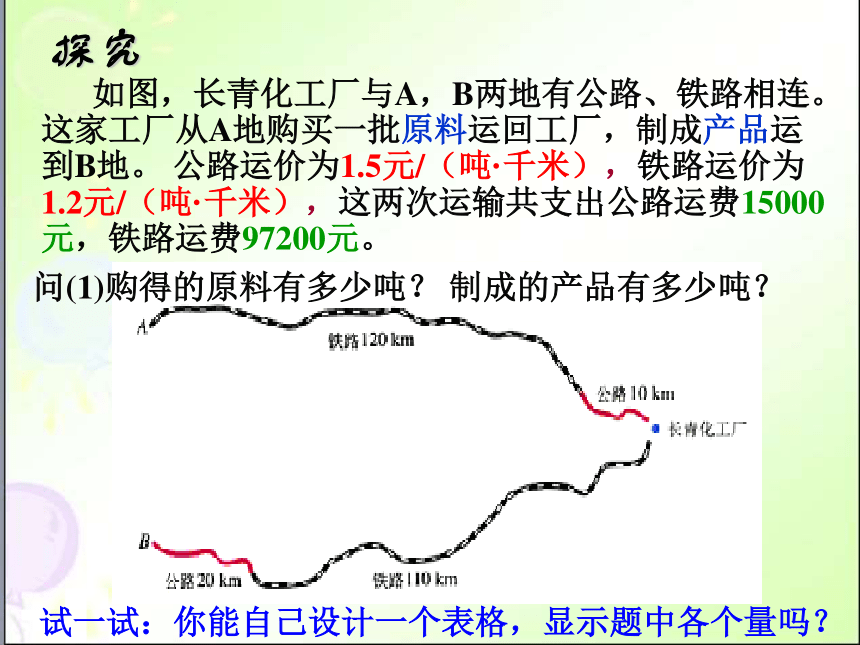
如图,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。 公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。
探究
问(1)购得的原料有多少吨? 制成的产品有多少吨?
试一试:你能自己设计一个表格,显示题中各个量吗?
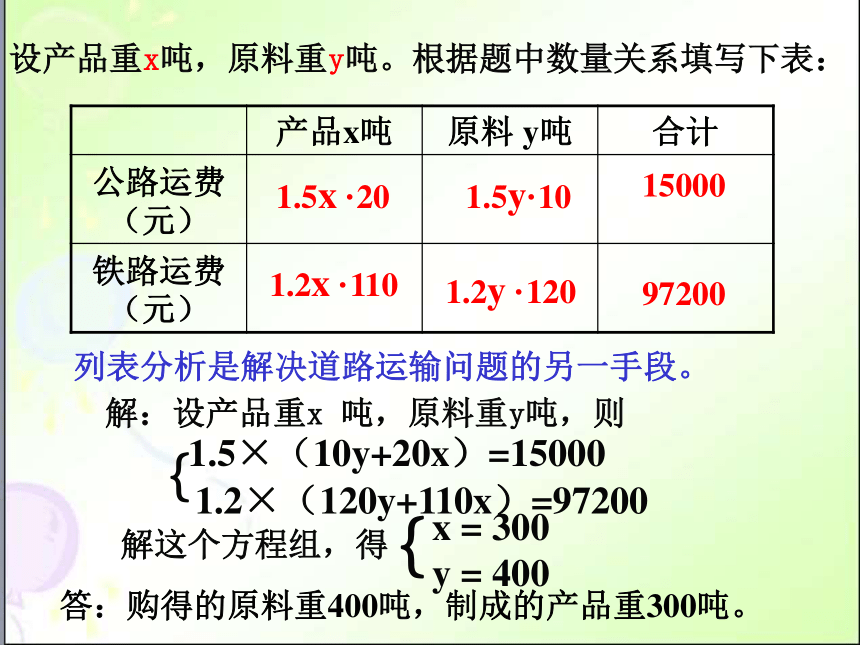
设产品重x吨,原料重y吨。根据题中数量关系填写下表:
产品x吨 原料 y吨 合计
公路运费(元)
铁路运费(元)
1.5y·10
1.5x ·20
1.2y ·120
1.2x ·110
15000
97200
列表分析是解决道路运输问题的另一手段。
解:设产品重x 吨,原料重y吨,则
1.5×(10y+20x)=15000
1.2×(120y+110x)=97200
{
解这个方程组,得
{
x = 300
y = 400
答:购得的原料重400吨,制成的产品重300吨。
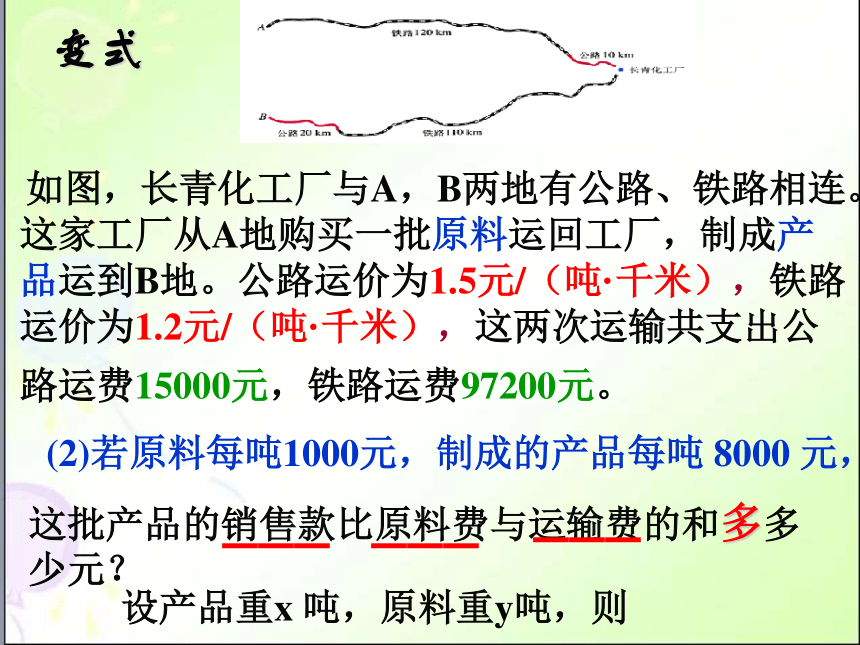
如图,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。
变式
(2)若原料每吨1000元,制成的产品每吨 8000 元,
这批产品的销售款比原料费与运输费的和多多少元?
___
___
___
设产品重x 吨,原料重y吨,则
8000x -(1000y+15000+97200)
=8000 × 300-(1000×400+15000+97200)
=1887800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元。
(2) 销售款-(原料费+运输费)
=
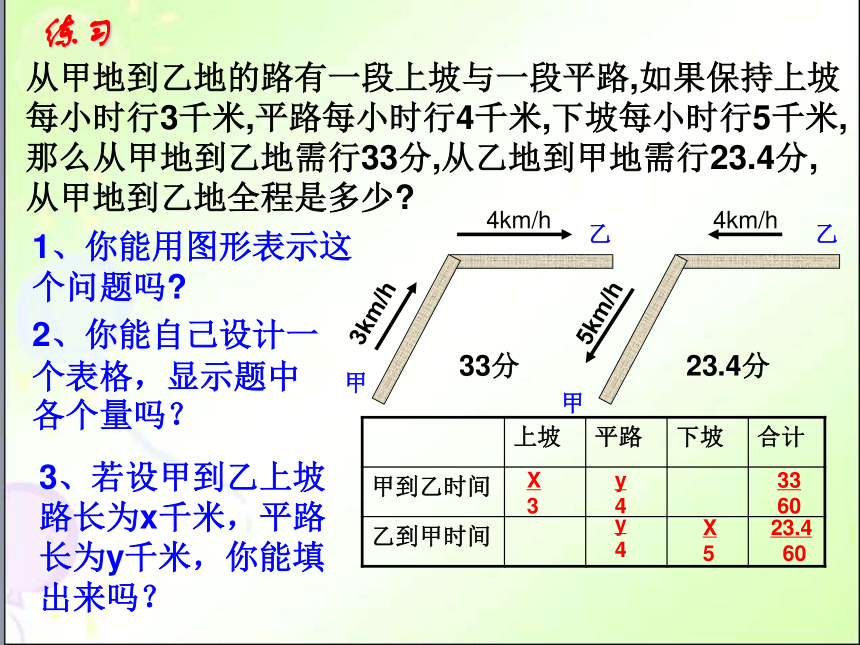
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行33分,从乙地到甲地需行23.4分,从甲地到乙地全程是多少
1、你能用图形表示这个问题吗
2、你能自己设计一个表格,显示题中各个量吗?
甲
乙
4km/h
3km/h
33分
乙
4km/h
5km/h
23.4分
甲
上坡 平路 下坡 合计
甲到乙时间
乙到甲时间
3、若设甲到乙上坡路长为x千米,平路长为y千米,你能填出来吗?
X
3
23.4
60
y
4
X
5
33
60
y
4
练习
某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售现牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题
商战风云再起
练习
其余5吨直接销售,获利500×5=2500(元) ∴共获利:8000+2500=10500(元)
方案二:设生产奶片用x天,生 产酸奶用y天
另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶
x+y=4
x+3y=9
x+y=9
x=1.5
y=2.5
x=1.5
y=7.5
方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000
1.5×1×2000+2.5×3×1200
=12000
∴共获利:
1.5×2000+7.5×1200
=3000+9000=12000
∴共获利:
商战风云再起
有两种药水,一种浓度为60%,另一种浓度为90%,现要配制浓度为70%的药水300g,则每种各需多少克?
浓度问题
关于浓度问题的概念:
溶液=溶质+溶剂
溶质=浓度×溶液
混合前溶液的和=混合后的溶液
混合前溶质的和=混合后的溶质
列方程组解应用题也要检验,既要代入方程组中,还要代入题目中检验。
依据是:
等量关系是:
两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精500克.每种酒精各需多少克
解此方程组,得
x=350
y=150
依题意,得
x+y=500
15% x+5% y=500×12%
即
x+y=500
3x+y=1200
答:甲种酒精取350克,乙种酒精取150克。
解:设甲种酒精取x克,乙种酒精取y克。
酒精重量
含水量
甲 种
乙 种
甲 种
乙 种
熔化前
熔化后
x克
y克
15%·x
5%·y
500克
500×12%
1、列方程组表示下列各题中的数量关系:
1.甲种矿石含铁的百分数是乙种矿石的1.5倍。甲种矿石5份,乙种矿石3份混合成的矿石含铁52.5%,设甲种为x%,乙种为y%,则
x%=1.5y%
5·x%+3 ·y%=(5+3) · 52.5%
2.两块含铝锡的合金,第一块含铝40克.含锡10克,第二块含铝3克.锡27克,要得到含铝62.5%的合金40克,取第一块为x克,第二块为y克,
则
x+y=40
40
40+10
·x+
3
3+37
·y=62.5%×40
3.甲.乙两种盐水各取100克混合,所得盐水含盐为10%,若甲种盐水取400克,乙种盐水取500克混合,所得盐水含盐为9%,设甲为x%,乙为y%,
则
100 ·x%+100 ·y%=2×100×10%
400 ·x%+500 ·y%=(400+500) ·9%
例5:有两种合金,第一种合金含金90%,第二种合金含金80%,这两种合金各取多少克,熔化以后才能得到含金82.5%的合金100克
合金重量
含金量
第一种
第二种
第一种
第二种
熔化前
熔化后
x克
y克
90%·x
80%·y
100克
100×82.5%
解:设第一种合金取x克,第二种合金取y克。
依题意,得
x+y=100
90% x+80% y=100×82.5%
即
x+y=100
9x+8y=825
解此方程组,得
x=25
y=75
答:第一种合金取25克,第二种合金取75克。
6、两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精500克.每种酒精各需多少克
解此方程组,得
x=350
y=150
依题意,得
x+y=500
15% x+5% y=500×12%
即
x+y=500
3x+y=1200
答:甲种酒精取350克,乙种酒精取150克。
解:设甲种酒精取x克,乙种酒精取y克。
酒精重量
含水量
甲 种
乙 种
甲 种
乙 种
熔化前
熔化后
x克
y克
15%·x
5%·y
500克
500×12%
7、列方程组表示下列各题中的数量关系:
1.甲种矿石含铁的百分数是乙种矿石的1.5倍。甲种矿石5份,乙种矿石3份混合成的矿石含铁52.5%,设甲种为x%,乙种为y%,则
x%=1.5y%
5·x%+3 ·y%=(5+3) · 52.5%
8.两块含铝锡的合金,第一块含铝40克.含锡10克,第二块含铝3克.锡27克,要得到含铝62.5%的合金40克,取第一块为x克,第二块为y克,
则
x+y=40
40
40+10
·x+
3
3+37
·y=62.5%×40
9.甲.乙两种盐水各取100克混合,所得盐水含盐为10%,若甲种盐水取400克,乙种盐水取500克混合,所得盐水含盐为9%,设甲为x%,乙为y%,
则
100 ·x%+100 ·y%=2×100×10%
400 ·x%+500 ·y%=(400+500) ·9%
请学生回顾这节课所学的关于浓度问题的概念
溶液=溶质+溶剂
溶质=浓度×溶液
混合前溶液的和=混合后的溶液
混合前溶质的和=混合后的溶质
列方程组解应用题也要检验,既要代入方程组中,还要代入题目中检验。
依据是:
等量关系是:
例8、用一些长短相同的小木棍按图所式,连续摆正方形或六边形要求每两个相邻的图形只有一条公共边。已知摆放的正方形比六边形多4个,并且一共用了110个小木棍,问连续摆放了正方形和六边形各多少个?
…
…
图形 连续摆放的个数
(单位:个) 使用小木棒的根数 (单位:根)
正方形 x 4+3(x-1)=3x+1
六边形 y 6+5(y-1)=5y+1
关系
正反方形比六边形多 4 个 共用了 110 根小木棍
…
…
某人用24000元买进甲、乙两种股票,在甲股票升值15%,乙股票下跌10%时卖出,共获利1350元,试问某人买的甲、乙两股票各是多少元?
二、行程类问题
1、某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
解:设甲乙两车的速度分别为x km/h、y km/h
根据题意,得
5y=6x
4y=4x+40
解之得
x=50
y=6o
答:甲乙两车的速度分别为50km/h、60km/h.
2、某跑道一圈长400米,若甲、乙两运动员从起点同时出发,相背而行,25秒之后相遇;若甲从起点先跑2秒,乙从该点同向出发追甲,再过3秒之后乙追上甲,求甲、乙两人的速度。
解:设甲、乙两人的速度分别为x米/秒,y米/秒,
根据题意得
解这个方程组得,
答:甲、乙两人的速度分别为6米/秒,10米/秒.
即
3、一艘轮船顺流航行45千米需要3小时,逆流航行65千米需要5小时,求船在静水中的速度和水流速度。
解:设船在静水中的速度为x千米/时,水流的速度为y千米/时,根据题意,得
答:船在静水中的速度及水流的速度分别为14千米/时、1千米/时.
解这个方程组得,
即
三、工程问题
1、某工人原计划在限定时间内加工一批零件.如果每小时加工10个零件,就可以超额完成3 个;如果每小时加工11个零件就可以提前1h完成.问这批零件有多少个 按原计划需多少小时 完成
解:设这批零件有x个,按原计划需y小时完成,根据题意得
解这个方程组得,
答:这批零件有77个,按原计划需8小时完成。
3、10年前,母亲的年龄是儿子的6倍;10年后,母亲的年龄是儿子的2倍.求母子现在的年龄.
解:设母亲现在的年龄为x岁,儿子现在的年龄为y岁,列方程组得
即
①
②
①-②,得
把y=15代入②,得x-2×15=10,
∴这个方程组的解为
答:母亲现在的年龄为40岁,儿子现在的年龄为15岁.
2、100个和尚分100个馒头,大和尚每人吃3个,小和尚每3人吃一个,问:大小和尚各有几个?
解:设大和尚x人,小和尚y人,则根据题意得
解这个方程组得,
答:大和尚75人,小和尚25人.
十一、探究题
1、某校初三(2)班40名同学为“希望工程”捐款,共捐款100元,捐款情况如下表:
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚。你能把它填进去吗?
捐款(元) 1 2 3 4
人 数 6 7
解:设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组是
解这个方程组得,
答:捐款2元的有15名同学,捐款3元的有12名同学.
8.3 实际问题与二元一次方程组(3)
走近生活 探究知识 享受快乐
1、公路的运价为1.5元/(吨·千米),
里程为10km,货物重量为200吨,
则公路运费= .
1.5×10×200
2、铁路的运价为1.2元/(吨·千米),
原料重量为100吨,里程为20km,
则铁路运费= .
1.2×20×100
探究:
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费
15000元,铁路运费97200元。求工厂从A地购得的原料
有多少吨?制成的产品有多少吨?
分析:题中的量很多,并且相互关联,这时,我们可画一张示意图,把题中的条件在图中标出来,这样比较直,能帮助我们比较顺利地找出题中的相等关系。
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
探究:
探究:
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),
这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
解:制成的产品为x 吨,设购得的原料为y吨,
根据题意得
{
1.5 × 80 ×y =15000
1.2×150 ×x =97200
解得:
{
x=540
y=125
答:购得的原料为125吨, 制成的产品为540 吨。
画示意图是解决道路运输问题的手段之一。
如图,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。 公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。
探究
问(1)购得的原料有多少吨? 制成的产品有多少吨?
试一试:你能自己设计一个表格,显示题中各个量吗?
设产品重x吨,原料重y吨。根据题中数量关系填写下表:
产品x吨 原料 y吨 合计
公路运费(元)
铁路运费(元)
1.5y·10
1.5x ·20
1.2y ·120
1.2x ·110
15000
97200
列表分析是解决道路运输问题的另一手段。
解:设产品重x 吨,原料重y吨,则
1.5×(10y+20x)=15000
1.2×(120y+110x)=97200
{
解这个方程组,得
{
x = 300
y = 400
答:购得的原料重400吨,制成的产品重300吨。
如图,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。
变式
(2)若原料每吨1000元,制成的产品每吨 8000 元,
这批产品的销售款比原料费与运输费的和多多少元?
___
___
___
设产品重x 吨,原料重y吨,则
8000x -(1000y+15000+97200)
=8000 × 300-(1000×400+15000+97200)
=1887800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元。
(2) 销售款-(原料费+运输费)
=
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行33分,从乙地到甲地需行23.4分,从甲地到乙地全程是多少
1、你能用图形表示这个问题吗
2、你能自己设计一个表格,显示题中各个量吗?
甲
乙
4km/h
3km/h
33分
乙
4km/h
5km/h
23.4分
甲
上坡 平路 下坡 合计
甲到乙时间
乙到甲时间
3、若设甲到乙上坡路长为x千米,平路长为y千米,你能填出来吗?
X
3
23.4
60
y
4
X
5
33
60
y
4
练习
某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售现牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题
商战风云再起
练习
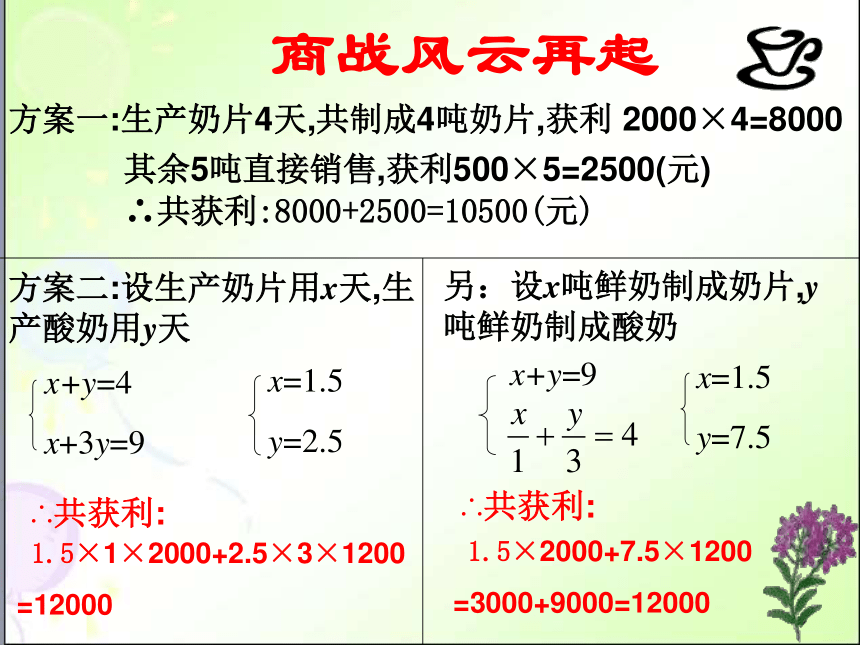
其余5吨直接销售,获利500×5=2500(元) ∴共获利:8000+2500=10500(元)
方案二:设生产奶片用x天,生 产酸奶用y天
另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶
x+y=4
x+3y=9
x+y=9
x=1.5
y=2.5
x=1.5
y=7.5
方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000
1.5×1×2000+2.5×3×1200
=12000
∴共获利:
1.5×2000+7.5×1200
=3000+9000=12000
∴共获利:
商战风云再起
有两种药水,一种浓度为60%,另一种浓度为90%,现要配制浓度为70%的药水300g,则每种各需多少克?
浓度问题
关于浓度问题的概念:
溶液=溶质+溶剂
溶质=浓度×溶液
混合前溶液的和=混合后的溶液
混合前溶质的和=混合后的溶质
列方程组解应用题也要检验,既要代入方程组中,还要代入题目中检验。
依据是:
等量关系是:
两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精500克.每种酒精各需多少克
解此方程组,得
x=350
y=150
依题意,得
x+y=500
15% x+5% y=500×12%
即
x+y=500
3x+y=1200
答:甲种酒精取350克,乙种酒精取150克。
解:设甲种酒精取x克,乙种酒精取y克。
酒精重量
含水量
甲 种
乙 种
甲 种
乙 种
熔化前
熔化后
x克
y克
15%·x
5%·y
500克
500×12%
1、列方程组表示下列各题中的数量关系:
1.甲种矿石含铁的百分数是乙种矿石的1.5倍。甲种矿石5份,乙种矿石3份混合成的矿石含铁52.5%,设甲种为x%,乙种为y%,则
x%=1.5y%
5·x%+3 ·y%=(5+3) · 52.5%
2.两块含铝锡的合金,第一块含铝40克.含锡10克,第二块含铝3克.锡27克,要得到含铝62.5%的合金40克,取第一块为x克,第二块为y克,
则
x+y=40
40
40+10
·x+
3
3+37
·y=62.5%×40
3.甲.乙两种盐水各取100克混合,所得盐水含盐为10%,若甲种盐水取400克,乙种盐水取500克混合,所得盐水含盐为9%,设甲为x%,乙为y%,
则
100 ·x%+100 ·y%=2×100×10%
400 ·x%+500 ·y%=(400+500) ·9%
例5:有两种合金,第一种合金含金90%,第二种合金含金80%,这两种合金各取多少克,熔化以后才能得到含金82.5%的合金100克
合金重量
含金量
第一种
第二种
第一种
第二种
熔化前
熔化后
x克
y克
90%·x
80%·y
100克
100×82.5%
解:设第一种合金取x克,第二种合金取y克。
依题意,得
x+y=100
90% x+80% y=100×82.5%
即
x+y=100
9x+8y=825
解此方程组,得
x=25
y=75
答:第一种合金取25克,第二种合金取75克。
6、两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精500克.每种酒精各需多少克
解此方程组,得
x=350
y=150
依题意,得
x+y=500
15% x+5% y=500×12%
即
x+y=500
3x+y=1200
答:甲种酒精取350克,乙种酒精取150克。
解:设甲种酒精取x克,乙种酒精取y克。
酒精重量
含水量
甲 种
乙 种
甲 种
乙 种
熔化前
熔化后
x克
y克
15%·x
5%·y
500克
500×12%
7、列方程组表示下列各题中的数量关系:
1.甲种矿石含铁的百分数是乙种矿石的1.5倍。甲种矿石5份,乙种矿石3份混合成的矿石含铁52.5%,设甲种为x%,乙种为y%,则
x%=1.5y%
5·x%+3 ·y%=(5+3) · 52.5%
8.两块含铝锡的合金,第一块含铝40克.含锡10克,第二块含铝3克.锡27克,要得到含铝62.5%的合金40克,取第一块为x克,第二块为y克,
则
x+y=40
40
40+10
·x+
3
3+37
·y=62.5%×40
9.甲.乙两种盐水各取100克混合,所得盐水含盐为10%,若甲种盐水取400克,乙种盐水取500克混合,所得盐水含盐为9%,设甲为x%,乙为y%,
则
100 ·x%+100 ·y%=2×100×10%
400 ·x%+500 ·y%=(400+500) ·9%
请学生回顾这节课所学的关于浓度问题的概念
溶液=溶质+溶剂
溶质=浓度×溶液
混合前溶液的和=混合后的溶液
混合前溶质的和=混合后的溶质
列方程组解应用题也要检验,既要代入方程组中,还要代入题目中检验。
依据是:
等量关系是:
例8、用一些长短相同的小木棍按图所式,连续摆正方形或六边形要求每两个相邻的图形只有一条公共边。已知摆放的正方形比六边形多4个,并且一共用了110个小木棍,问连续摆放了正方形和六边形各多少个?
…
…
图形 连续摆放的个数
(单位:个) 使用小木棒的根数 (单位:根)
正方形 x 4+3(x-1)=3x+1
六边形 y 6+5(y-1)=5y+1
关系
正反方形比六边形多 4 个 共用了 110 根小木棍
…
…
某人用24000元买进甲、乙两种股票,在甲股票升值15%,乙股票下跌10%时卖出,共获利1350元,试问某人买的甲、乙两股票各是多少元?
二、行程类问题
1、某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
解:设甲乙两车的速度分别为x km/h、y km/h
根据题意,得
5y=6x
4y=4x+40
解之得
x=50
y=6o
答:甲乙两车的速度分别为50km/h、60km/h.
2、某跑道一圈长400米,若甲、乙两运动员从起点同时出发,相背而行,25秒之后相遇;若甲从起点先跑2秒,乙从该点同向出发追甲,再过3秒之后乙追上甲,求甲、乙两人的速度。
解:设甲、乙两人的速度分别为x米/秒,y米/秒,
根据题意得
解这个方程组得,
答:甲、乙两人的速度分别为6米/秒,10米/秒.
即
3、一艘轮船顺流航行45千米需要3小时,逆流航行65千米需要5小时,求船在静水中的速度和水流速度。
解:设船在静水中的速度为x千米/时,水流的速度为y千米/时,根据题意,得
答:船在静水中的速度及水流的速度分别为14千米/时、1千米/时.
解这个方程组得,
即
三、工程问题
1、某工人原计划在限定时间内加工一批零件.如果每小时加工10个零件,就可以超额完成3 个;如果每小时加工11个零件就可以提前1h完成.问这批零件有多少个 按原计划需多少小时 完成
解:设这批零件有x个,按原计划需y小时完成,根据题意得
解这个方程组得,
答:这批零件有77个,按原计划需8小时完成。
3、10年前,母亲的年龄是儿子的6倍;10年后,母亲的年龄是儿子的2倍.求母子现在的年龄.
解:设母亲现在的年龄为x岁,儿子现在的年龄为y岁,列方程组得
即
①
②
①-②,得
把y=15代入②,得x-2×15=10,
∴这个方程组的解为
答:母亲现在的年龄为40岁,儿子现在的年龄为15岁.
2、100个和尚分100个馒头,大和尚每人吃3个,小和尚每3人吃一个,问:大小和尚各有几个?
解:设大和尚x人,小和尚y人,则根据题意得
解这个方程组得,
答:大和尚75人,小和尚25人.
十一、探究题
1、某校初三(2)班40名同学为“希望工程”捐款,共捐款100元,捐款情况如下表:
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚。你能把它填进去吗?
捐款(元) 1 2 3 4
人 数 6 7
解:设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组是
解这个方程组得,
答:捐款2元的有15名同学,捐款3元的有12名同学.
